大断面小净距浅埋隧道围岩的屈服接近度分析
2018-05-09钟明文戴永浩
钟明文,武 松,邓 琴,汤 华,戴永浩
(1.云南大永高速公路建设指挥部, 云南 大理 671000;2.中国科学院 武汉岩土力学研究所 岩土力学与工程国家重点实验室, 湖北 武汉 430071;3.中国科学院大学, 北京 100000)
随着我国“丝绸之路经济带”和“长江经济带”等国家战略计划的实施,掀起了我国西部蓬勃的交通建设高潮。西部独特的人文地理特征,使得大部分高速公路/铁路的桥隧比例高达70%~80%[1],隧道建设成为西南山区交通建设的重中之重。
隧道的围岩稳定性评价一直是隧道建设的重点。隧道在开挖过程中,其围岩的应力和位移一直处于更新状态,需要不断地根据应力或者位移信息来评价围岩的稳定状态[2]。目前关于隧道的围岩稳定性评价方法很多,但从数据来源看主要有以下两大类:
(1) 根据现场监测数据的评价:隧道开挖过程中位移监测是必不可少的,通常辅以应力监测[3]。《公路隧道设计规范》[4](JTG D70—2004)给出不同的围岩级别下,不同埋深的隧道允许洞周水平相对收敛和拱顶下沉的建议值[4]。实际工程中,需要根据围岩地质条件综合分析确定。朱永全[5]、吴秋军等[6]、李晓红等[7]等均对此开展过研究。
(2) 根据计算分析的评价:该方法主要是以应力状态来分析,如万明富等[8]、王宇等[9]、王薇等[10]提出以单轴应力强度来判断围岩的稳定提性,本质上都是传统材料力学的经典强度分析理论和强度储备计算方法。潘昌实[11]根据Mohr-Coulomb准则对高斯点的强度发挥系数进行了研究。Fairburst C[12]根据摩尔抛物型包络线准则提出了二维应力状态下破坏接近度的定义,最早在1964年提出破坏接近度的概念。金丰年等[13]于1996年在Fairburst的基础上提出了二维及三维应力状态下的破坏接近度的定义。杜丽惠等[14]引入破坏接近度的概念来反应单元材料的非线性特征;周辉等[2]和张传庆[15]提出了屈服接近度的新概念,通过分析主应力空间中屈服面和未屈服应力点两者的相互关系,来描述非塑性区的危险程度。此概念的提出,得到了广泛的应用[16-18],并拓展至岩质边坡的稳定性研究[19-20]。
本文以甸头隧道近距离下穿大西公路路段为依托,采用周辉等提出的概念,分析隧道施工过程中隧道围岩的屈服接近度的演化和转移特征,并和围岩塑性区的发展过程比较,来开展围岩的稳定性研究。
1 工程概况
1.1 工程概述
华坪至丽江高速公路连接段大理连接线工程大理段(以下简称“大永高速公路”)向北可以连接正在规划实施的华丽高速公路,南入大理市连接楚大、大保、大丽高速公路,是连通滇西现有的所有高速中通达效果最好、连通功能最强的联络线,对促进地区经济发展具有重要作用。
甸头隧道位于大永高速公路的大理至宾川段,设计为分离式双向六车道公路隧道。左右幅隧道净距离为28.21 m~29.00 m,隧道净宽15.4 m,净高5.0 m,属于超大断面隧道。甸头隧道与大西二级公路存在两处交叉,分别交叉于左幅的ZK6+997—ZK7+012段和右幅的YK7+030—YK7+045段。左、右幅隧道交叉点埋深均为10 m~14 m,属于近距离交叉工程。
甸头隧道近距离下穿的大西二级公路为连接大理市和宾川县的唯一通道,沿线砂石料厂、水泥厂分布较多,周围人口密集,交通量日均高达3万辆,其中重型车和超限车约80%,该路安全畅通对于人民群众生产、生活具有十分重要的作用。
1.2 地质情况
为获取隧道下穿公路段的地质情况,在隧道下穿公路时进口和出口段布置钻孔,土层自上至下分别是历史填土、全风化玄武岩和强风化玄武岩。其中历史填土呈现黄褐色、褐灰色,全风化玄武岩呈现黄褐色灰褐色,岩芯呈土状;强风化玄武岩灰褐色,隐晶—细粒结构,块状构造。
1.3 施工方案
甸头隧道下穿大西二级公路段采用三台阶法进行施工。超前支护措施分为小导管注浆和超前大管棚:超前管棚采用Φ108 mm×6,长15 m,环向间距30 cm;超前小导管采用Φ42 mm×4,长5.0 m,环向间距40 cm,设置于衬砌拱部约120°范围;初期支护:由喷射混凝土(C30,厚度为29 cm)、径向锚杆(长度4.5 m,间距为1.0 m×0.6 m)、钢筋网(8@150 mm×150 mm)及工字钢钢架(间距50 cm)组成;二衬采用C30钢筋混凝土结构,厚度70 cm,以确保隧道支护结构的安全。支护措施见图1和图2。
上台阶开挖进尺为每循环0.5 m~1.0 m,采用机械开挖,以确保现场施工安全。
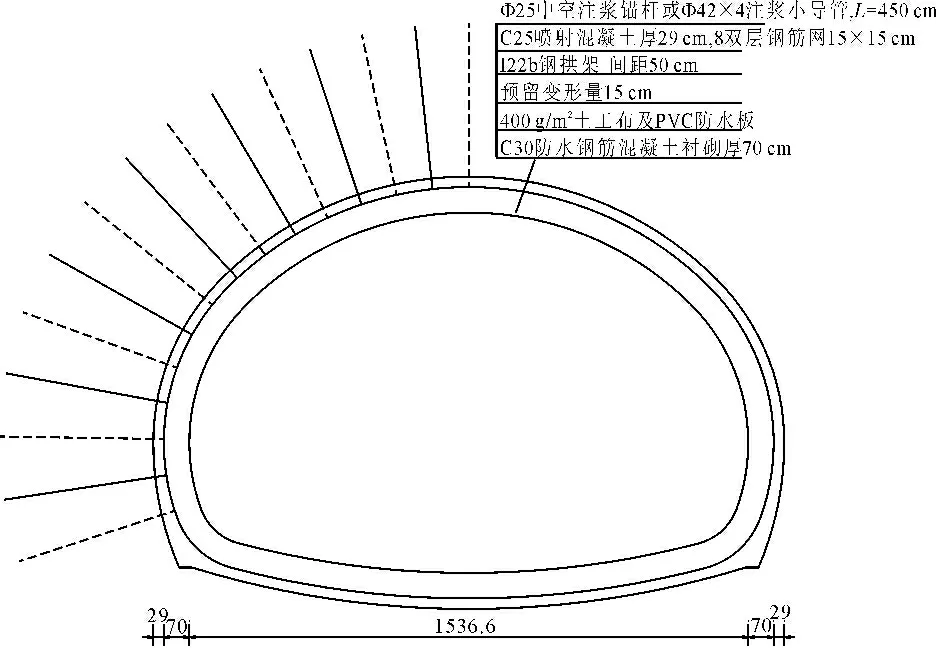
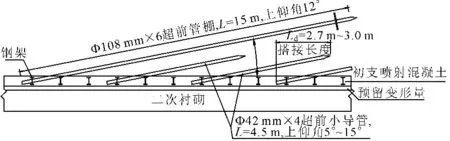
图1 穿越段衬砌段面示意图(单位:cm)
图2超前支护措施纵断面示意图
2 屈服接近度函数
Mohr-Coulomb准则在前岩土工程中应用广泛,本文考虑岩土体为理想弹塑性模型,满足Mohr-Coulomb强度准则,其在主应力空间的表达式为:
(1)
式中:I1、J2分别是应力张量的第一和第二不变量;θσ为应力罗德角;c和φ分别代表岩土体的黏聚力和内摩擦角。
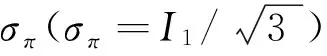
F(σπ,τπ,θσ)=Aσπ+B(θσ)τπ+D
(2)
其中
(3)
(4)
D=-ccosφ
(5)
根据上述表达式可以看出,主应力空间的任意一点均可以表示为子午面和π平面上的一点,以A点为例,如图3、图4所示。
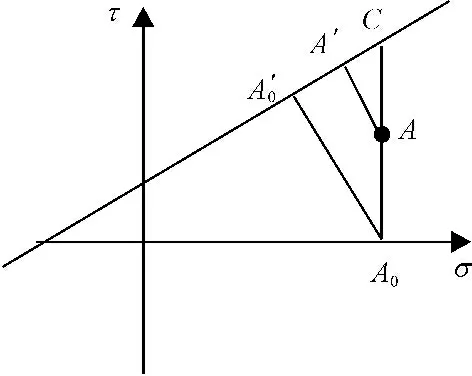
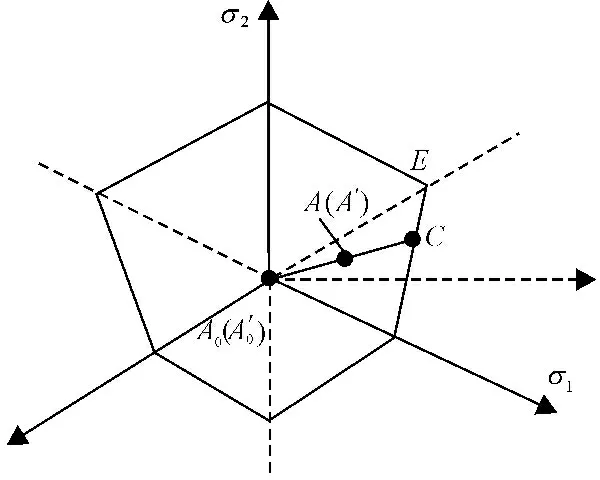
图3 子午面上一点的应力状态
图4平面上一点的应力状态
(6)
其中C点位于屈服面上,因此坐标满足关系式(2),因此
(7)
将式(7)代入式(6),可得
(8)
可以看出,当应力点在屈服面上时,f=0,在等倾线上时,f=1。因此,屈服接近度为描述一点的现时状态与相对最安全状态的参量的比,其取值范围为[0,1]。
图5是σ-τ平面内的Mohr圆与剪切包络线和拉伸包络线的关系示意图,同时考虑剪切和拉伸破坏两种情况。直线BC和BD同为圆1切线,P点是圆心。当圆2的圆心处在点圆1的圆心左侧(或右侧)时,对应只考虑剪切(或拉伸)屈服,此时屈服接近度的计算公式为:
(9)
因此,同时考虑剪切和拉伸的屈服接近度函数为:
(10)
其中σR为图5中点P的正应力。
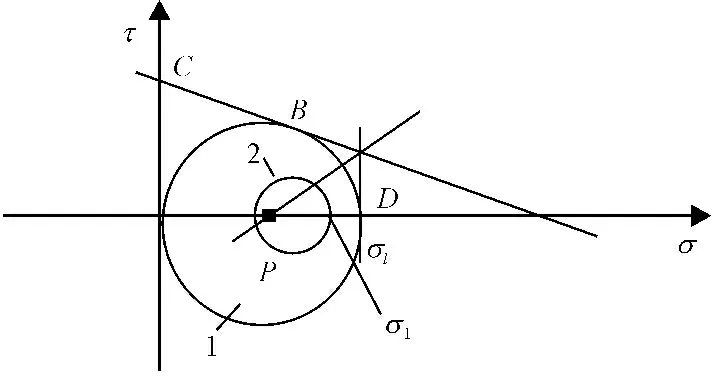
图5拉伸-剪切破坏的分析图
根据上述推导的屈服接近度公式,采用FLAC3D编写Fish程序,分析甸头隧道下穿公路段的岩体屈服接近度的演化,并和塑性区发展相比较,来研究隧道围岩的稳定性。
3 计算分析
选取甸头隧道下穿公路的进口段建立二维模型,如图6所示。其中模型的长度和宽度选取充分考虑边界效应的影响。根据上述的地质概况,隧道围岩自上至下分别是碎石土、全风化和强风化玄武岩。
根据地质勘察,室内试验和工程类比,确定隧道围岩及加固措施的力学参数如表1所示。
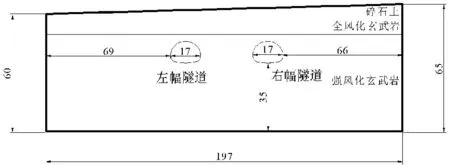
图6模型示意图(单位:m)
数值计算中,围岩采用弹塑性本构和Mohr-Coulomb强度准则。锚杆和初衬混凝土采用弹性模型。由于隧道处于浅埋状态,因此只考虑因岩体重力引起的初始地应力。实际中,隧道开挖属于三维问题。当采用二维问题进行模拟时,就必须考虑应力释放率[15]的问题。根据围岩类型和文献参考,考虑隧道开挖时应力释放30%,施加初支后释放70%。
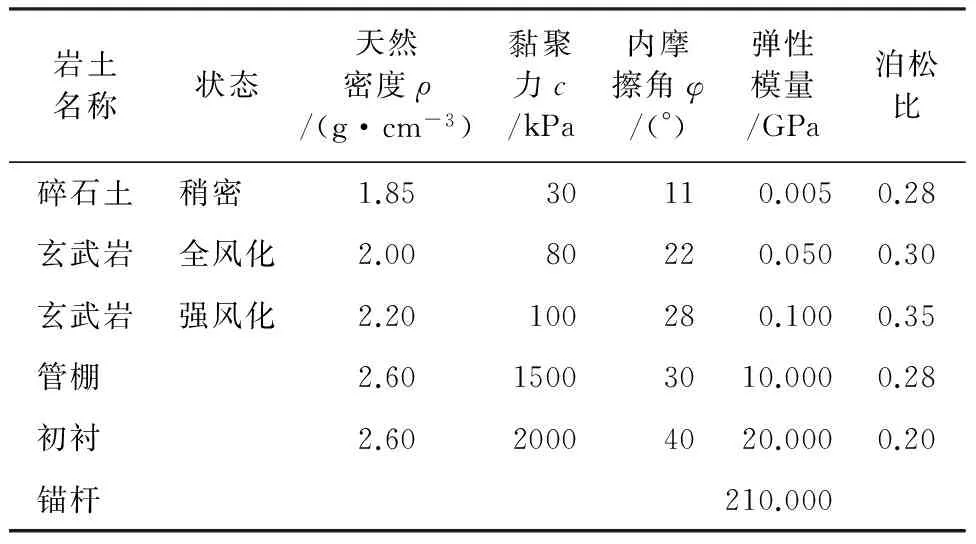
表1 岩土力学参数表
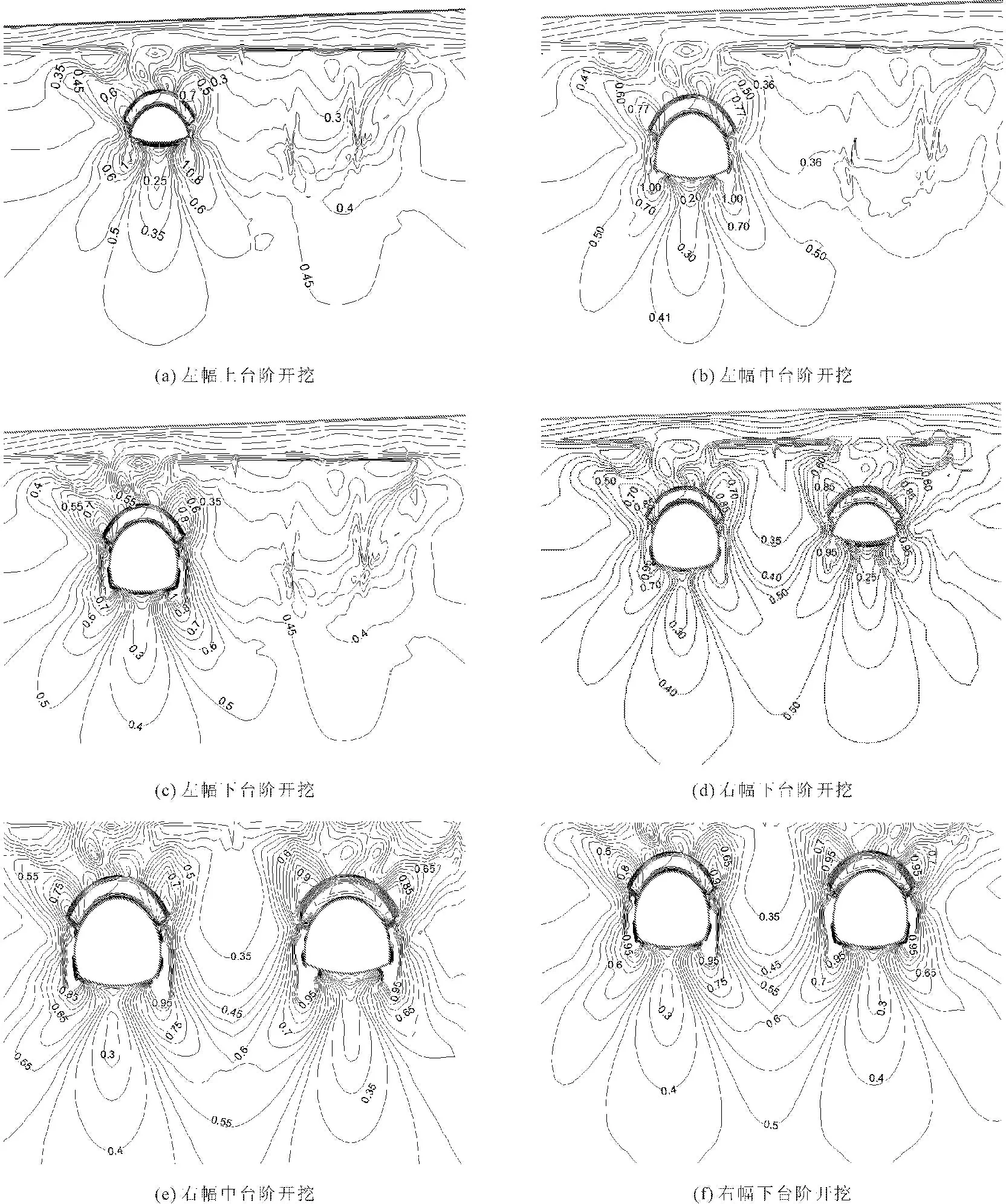
图7不同开挖步下的隧道围岩屈服接近度
图7展示了不同开挖步下的隧道围岩屈服接近度(YAI)分布情况。需要注意的是,这里为了和塑性区相对应,选取1-YAI作为新的屈服接近度指标。因此,塑性区主要是屈服接近度为1的区域,越靠近该区域,危险性程度越高。
从图7中可以看出:
(1) 台阶法开挖时,每级台阶开挖支护后,屈服接近度为1的区域都主要集中在拱脚部位。
(2) 拱顶处由于管棚超前支护和超前小导管注浆的作用,其屈服接近度很小。然而,加固区顶部的周边围岩由于隧道的开挖其屈服接近度急剧增大。
(3) 由于左幅隧道开挖的影响,使得右幅隧道的加固区附近围岩大于左幅隧道相应位置的屈服接近度。
(4) 隧道开挖完毕,右幅隧道大于左幅隧道周边围岩屈服接近度为1的区域,即右幅隧道大于左幅隧道进入塑性的围岩区域,这和塑性区分布图一致(见图8)。
如果将屈服接近度大于0.7的屈服划分为重点关注区域,则该隧道的关注区域如图9所示,即:隧道拱腰周边的围岩。根据隧道支护情况,目前锚杆加固的范围基本涵盖了关注区域的范围,仅在拱脚附近需要加长锚杆的长度。
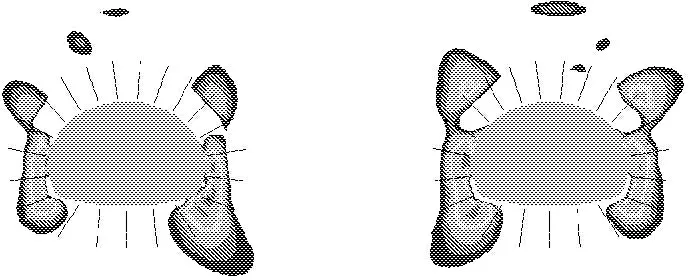
图8 围岩的塑性区分布
图9关注区域
4 结 论
依据周辉等提出的屈服接近度的定义,针对甸头隧道下穿大西公路段,采用平面模型开展了隧道开挖过程中屈服接近度的计算和转移分析,并和围岩的塑性区发展过程相比较,开展围岩的稳定性研究。根据研究结果,提出针对拱脚附近需要加长锚杆的长度,以保证围岩的整体稳定性。
参考文献:
[1] 左亚飞.新建公路工程下穿既有高速铁路桥梁影响的研究[D].北京:北京交通大学,2016.
[2] 周 辉,张传庆,冯夏庭,等.隧道及地下工程围岩的屈服接近度分析[J].岩石力学与工程学报,2005,24(17):3083-3087.
[3] 张国华,陈礼彪,钱师雄,等.大断面小净距大帽山隧道现场监控量测及分析[J].岩土力学,2010,31(2):489-496.
[4] 公路隧道设计规范:JTG D70—2004[S].北京:人民交通出版社,2004.
[5] 朱永全.隧道稳定性位移判别准则[J].中国铁道科学,2001,22(6):80-83.
[6] 吴秋军,王明年,刘大刚.基于现场位移监测数据统计分析的隧道围岩稳定性研究[J].岩土力学,2012,33(S2):359-364.
[7] 李晓红,王宏图,贾剑青,等.隧道及地下工程围岩稳定性及可靠性分析的极限位移判别[J].岩土力学,2005,26(6):850-854.
[8] 万明富,党为民,李云祥.阿家岭隧道围岩稳定性的边界元法分析[J].东北公路,1996(2):68-70.
[9] 王 宇,罗 毅.凌子口隧道围岩稳定性分析评价[J].地质灾害与环境保护,2002,13(3):40-42.
[10] 王 薇,王连捷,王红才,等.青藏铁路昆仑山隧道稳定性分析[J].地球学报,2002,23(4):359-362.
[11] 潘昌实.隧道力学数值方法[M].北京:中国铁道出版社,1995.
[12] Fairburst C. On the validity of the Brazilian test for brittle materials[J]. Int J. Rock Mech in Sci., 1964,1(4):535-546.
[13] 金丰年,浦奎英.破坏接近度的定义及其应用[J].工程力学,1996(S1):626-630.
[14] 杜丽惠,黄丽清.考虑围岩蠕变特性的轴对称有限元非线性分析[J].水利学报,2001,32(1):85-89.
[15] 张传庆.基于破坏接近度的岩石工程安全性评价方法的研究[D].武汉:中国科学院武汉岩土力学研究所,2006.
[16] 李文渊,吴启红.基于JRC-JCS模型的屈服接近度及地下工程围岩稳定性分析方法[J].岩土力学,2012,33(S1):19-24.
[17] 舒谷生,彭文祥.非线性准则下节理岩体稳定性的屈服接近度分析[J].中南大学学报(自然科学版),2010,41(5):1883-1886.
[18] 柳群义,朱自强,钟正强,等.基于Hoek-Brown准则的隧道围岩屈服接近度分析[J].岩土力学,2009,30(8):2447-2451.
[19] 周 蕊,晏华斌,吴 剑,等.基于破坏接近度的滑坡倾斜加载方式破坏相似性研究[J].长江科学院院报,2017,34(3):74-79.
[20] 胡明军.基于破坏接近度的岩质边坡稳定性分析[D].重庆:重庆交通大学,2010.
