正交异性膜结构在冲击荷载作用下的振动解析与数值分析

张 琳，何 玲， 庞 嵩，刘长江

(1.中铁二院工程集团有限责任公司，四川成都 610031； 2. 成都理工大学，四川成都 610059)

张拉平面膜结构主要用于会展中心、停车场和体育馆等公共设施的平面型屋盖结构中[1]。由于这种结构自重轻、刚度小，因而在外荷载作用下容易产生振动，以致膜面松弛变形，甚至导致整个膜结构失效。因此对膜结构的动力设计进行优化控制具有重要意义。

目前，国内外学者对薄膜结构自由振动作了一定的研究。1999年，Vega等对带有内部斜撑的矩形薄膜的自由振动进行了研究，得到了其振动频率的解析解[2]。2002年和2004年，Kang等对倾斜和弯曲复合矩形薄膜的自由振动进行了研究，得到了倾斜度和弯曲度对其振动频率的影响[3]。2009年，Reutskiy发展了一种新的数值分析方法对任意形状的薄膜的非线性振动进行了研究，该方法基于频谱分析系统物理响应的数学模拟[4]。在国内，2010年，林文静等构造六节点三角形单元，用于平面薄膜自由振动的有限元分析，给出了三个典型算例表明，六节点三角形单元的计算结果比ANSYS三角形单元更接近理论解，即六节点三角形单元具有更高的精度[5]。

以上的这些研究都是针对均匀的膜结构进行的研究，且没有进行冲击荷载下膜结构的受迫振动的研究。因此，本文将采用近似解析方法和数值分析对正交异性的平面张拉建筑膜结构在冲击荷载下的无阻尼受迫振动问题进行研究，为膜结构的动力设计提供一定的理论依据。

1 建立振动控制方程

开展正交异性的平面张拉建筑膜结构在冲击荷载下的无阻尼受迫振动问题的理论研究，核心任务是确定冲击荷载，并建立振动控制方程。

1.1冲击荷载

四边固支的正交异性矩形薄膜结构的x方向边长为a，y方向的边长为b，x方向初始拉力为Nox，y方向初始拉力为Noy，冲击荷载为一垂直于膜面入射的小球，其质量为M，初始速度为v0，如图1所示。当冲击点位于膜面上的点(x0,y0)处时，冲击荷载可表示为：

p(x,y,t)=F(t)δ(x-x0)(y-y0)

(1)

其中，F(t)为膜面所受冲击力；δ(x)为Dirac函数。

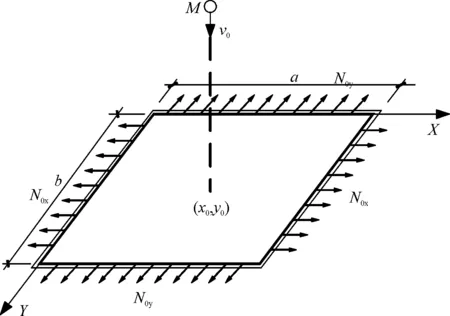
图1 四边固支的正交异性矩形薄膜受小球撞击示意

冲击荷载是在一很短的时间内作用的荷载，因此将小球与膜面的碰撞视为弹性碰撞，根据动量定理建立冲击力F(t)与薄膜挠度w(x,y,t)的关系式，有：

(2)

对式(2)求一次导计算，得：

(3)

1.2 控制方程和边界条件

根据结构动力学达朗贝尔原理[6]和冯·卡门大挠度理论[7-8]，便可以得到正交异性矩形薄膜在冲击荷载作用下的运动和受迫振动控制方程，通过推理获得受迫振动控制方程组简化式：

(4)

(5)

式中：N0x表示x向预张力；N0y表示y向预张力；Nx表示x向拉力；Ny表示y向拉力；w=w(x,y,t)为薄膜挠度；ρ为膜材的面密度。

2 控制方程求解

对已建立的受迫振动控制方程进行求解，得到振动位移函数。设振动位移函数和应力函数的表达式如下：

(6)

(7)

式(6)中:0≤x≤a，0≤y≤b，a和b分别为薄膜的长短边长度；φmn(x,y)和Tmn(t)为未知函数；Tmn(t)为时间的函数，它反映振动随时间变化的规律；m和n取正整数，表示x方向和y方向的正弦半波数或称为节线数。

为简化运算符号，令Tmn(t)=T(t)，φ(x,y,t)=φ，φmn(x,y)=φ(x,y)=φ，Wmn(x,y)=W(x,y)=W=sin(mπx/a)sin(nπy/b

将式(6)、式(7)只取其中的一项进行计算，再将最终得到的结果按照式(6)、式(7)式进行求和计算，即：

w(x,y,t)=T(t)·W(x,y)

(8)

φ(x,y,t)=T2(t)·φ(x,y)

(9)

把式(9)代入式(5)得：

(10)

根据式(10)的结构，设满足式(10)的解有如下形式：

γ1x3+γ2x2+γ3y3+γ4y2

(11)

将式(11)代入式(10)得：

(12)

下面计算冲击薄膜的瞬间，薄膜与小球一起运动的初速度。在冲击时，冲击时间非常短暂，薄膜与小球组成的系统近似为保守系统，动量守恒定理适用。考虑膜面不同点的速度的不同，则有：

(13)

其中，W为薄膜的初始变形函数。v0为小球的初速度，v0′为小球与薄膜冲击点在t=0时刻的初始速度。设薄膜初始变形的形函数为：

(14)

将式(14)代入式(13)，计算可得：

(15)

将式(1)、式(7)和式(8)代入式(4)，由伽辽金法得[9]：

(16)

将应力函数表达式(12)代入式(16)并进行简化得：

(17)

将式(3)代入式(17)并简化得：

(18)

方程式(18)是关于T(t)的非线性微分方程，其精确解析解很难求解。因此，采用L-P摄动法求解非线性方程式(18)的近似解析解，可得：

T(τ)=T0(τ)+εT1(τ)+0(ε2)=

(19)

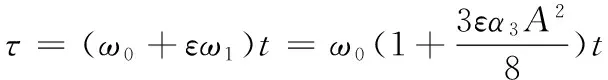
(20)

设在t=0时刻，薄膜冲击点与冲击物体有相同的初速度v0′，即令初始条件为：

(21)

将式(21)代入(20)式得：

(22)

求解可得：

(23)

将式(23)代入式(22)，可得：

(24)

将式(23)、式(24)代入式(20)得：

(25)

将式(25)代入双Fourier级数展开的位移表达式(6)得薄膜受迫振动位移函数：

(26)

3 数值计算与理论推导结果对比分析

为验证理论推导过程和结果的可靠性，采用大型通用有限元分析软件ANSYS中的LS-DYNA计算模块进行数值计算，并将解析理论分析结果与数值计算结果进行比较分析。计算参数：工程中常用的建筑膜材，面密度ρ为1.7 kg/m2；膜材厚度h为1 mm；膜材长宽分别为a=0.4 m和b=0.2 m,x和y方向的弹性模量分别为E1=1.4×106kN/m2，E2=0.9×106kN/m2，膜材预张力为N0x=N0y=10 kN/m，小球质量M为10-2kg。

3.1 位移时程曲线对比

将膜面冲击点无阻尼振动理论分析时程曲线和数值计算时程曲线绘入图2中进行对比。图2中 曲线横坐标单位为秒(s)，纵坐标：理论分析单位为米(m)，数值计算单位为毫米(mm)。

从图2可以看出，理论计算的时程曲线与数值分析的时程曲线很接近，只是冲击点的最大位移理论值略小于数值计算值。

3.2 最大位移值对比

薄膜在小球v0=15 m/s冲击作用下的位移云图如图3所示。从数值计算结果和理论计算结构中读取薄膜的最大位移值，并将其列入表1中对比分析，计算数值计算结果与理论分析结果的相对差。

从表1可以看出，数值计算的最大位移与理论分析最大位移相差较小，最大相对差为仅11.9 %。由此可知，数值计算结果与理论分析结果吻合良好。数值结果与理论结果的相对差值随着小球初速度的增加而减小，且理论计算结果略小于数值分析结果。

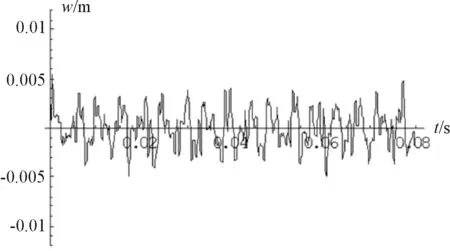
(a)理论分析曲线

(b)数值计算曲线图2 膜面冲击点的无阻尼振动时程曲线(v0=15m/s)

图3 薄膜位移云图(v0=15m/s)

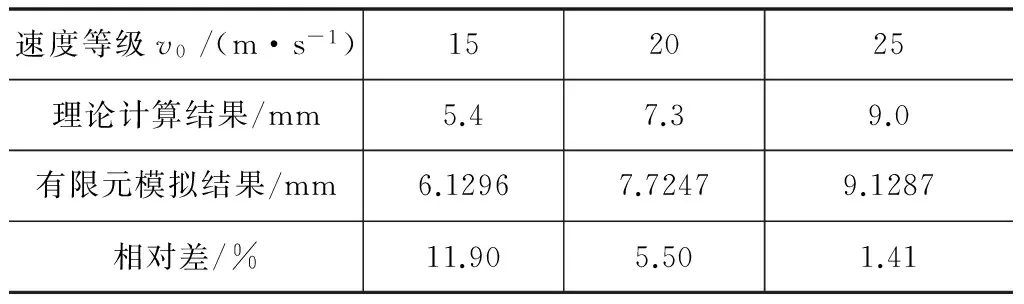
速度等级v0/(m·s-1)152025理论计算结果/mm5.47.39.0有限元模拟结果/mm6.12967.72479.1287相对差/%11.905.501.41

4 结论

本文利用达朗贝尔原理和薄膜大挠度理论，建立了四边固支矩形正交异性膜结构在冲击荷载作用下的非线性无阻尼振动的理论分析模型和控制方程组。采用L-P摄动法求解了所得控制方程租，得到了振动频率表达式和振动的位移函数表达式。采用ANSYS中的LS-DYNA模块进行了数值计算，并通过算例将理论推导公式解析解与数值计算结果进行了比较分析，从而验证了理论分析的准确性。本文建立的正交异性膜结构在冲击荷载作用下的振动解析理论计算方法对膜结构的动力分析和设计具有一定的理论指导意义和实用价值。

[1] 陈务军. 膜结构工程设计[M]. 北京: 中国建筑工业出版社, 2004.

[2] D. A. Vega, S. A. Vera, and P. A. A. Laura. Fundamental frequency of vibration of rectangular membranes with an internal oblique support[J]. Journal of Sound and Vibration, 1999, 224(4): 780-783.

[3] S. W. Kang and J. M. Lee. Free vibration analysis of composite rectangular membranes with an obliqueinterface[J]. Journal of Sound and Vibration, 2002, 251(3): 505-517.

[4] S. Yu. Reutskiy. Vibration analysis of arbitrarily shaped membranes[J]. CMES-Computer Modeling in Engineering & Sciences, 2009, 51(2): 115-142.

[5] 林文静，陈树辉. 平面薄膜自由振动的有限元分析[J]. 动力学与控制学报，2010, 8(3): 202-206.

[6] (美)R. 克拉夫, J. 彭津. 结构动力学[M].2版. 王光远，译. 北京: 高等教育出版社, 2006.

[7] Z.L. Zheng, C.J. Liu, X.T. He, et al., Free vibration analysis of rectangular orthotropic membranes in large deection, Math. Probl. Eng. 2009 (2009) Article ID 634362, 9 pages.

[8] C.J. Liu, Z.L. Zheng, X.T. He, et al., L-P Perturbation Solution of Nonlinear Free Vibration of Prestressed Orthotropic Membrane in Large Amplitude, Math. Probl. Eng. 2010 (2010) Article ID 561364, 17 pages.

[9] C. Shin, W. Kim and J. Chung. Free in-plane vibration of an axially moving membrane [J]. Journal of Sound and Vibration, 2004, 272: 137-54.