考虑稳定路线约束的零散货物拼车配送方案优化
2018-05-09肖文涛宫向阳
肖文涛,宫向阳
(1.中国石油化工股份有限公司大连石油化工研究院,辽宁 大连 116045;2.中国石油化工集团公司信息化管理部,北京 100728)
1 引言
物流配送是物流业务的一个重要环节。为降低物流成本和提高服务质量,需要优化调配车辆和合理选择路线。当前运输车辆逐渐大型化,配送需求逐渐个性化,为调和运输车辆大型化和配送需求零散化之间的矛盾,需要采用相关方法,优化拼装-配送方案。关于车辆路径优化问题的研究成果较多[1-5],但大多是在车型固定或数量确定等前提条件下得出的。随着运输业务外包趋势的发展,多车型、无限量、稳定路线、有限时间约束等复杂要求逐渐增多,现有研究结论不能满足新的优化需求。基于此,本文提出了一种基于稳定路线约束的零散货物多车型拼装配送方案优化方法。
2 问题简介
从远洋物流到陆地物流,从大宗商品、工业产品到农副食品运输,很多行业都存在拼装配送业务[4-7]。本文以某公司为客户配送产品为例,介绍优化需求及求解算法。某公司生产有保质期要求的食品,需要优化车辆选型及配送路线,为客户提供快速配送服务。物流配送业务的主要信息和相关要求如下文所述。
(1)车型信息。可供选用的车型有7种,各种车型无限量租用,其运量上限和费率见表1。各型车辆行驶速度都为50km/h,卸货速度为3t/h。
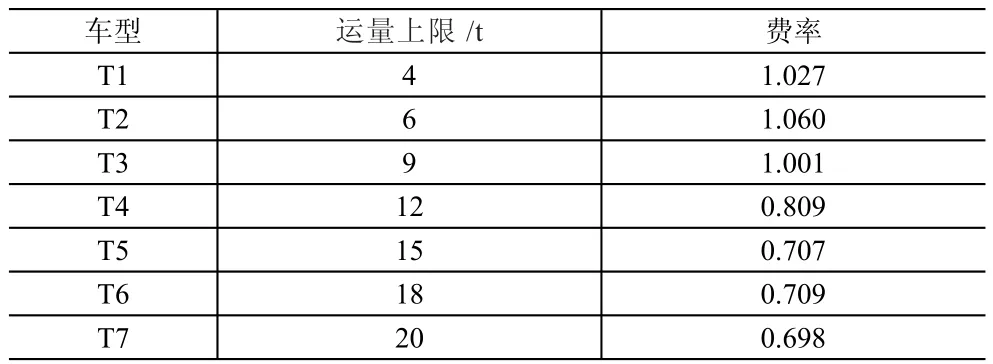
表1 各型车辆运量上限和费率表
(2)客户信息。客户总数共计83个,但由于A8、A31、A34、A46等4个客户已与运输公司约定同车统一配送,因而本文只考虑剩余的79个客户,各客户每次的货物需求量及收货频次见表2。
收货频次可分1、2、4三种类型。其中频次1指该客户每天需接收一次货物,频次2指该客户每两天需接收一次货物,同理频次4指该客户每四天需接收一次货物。
要求参与运输的各车从同一配货中心出发,沿各自的规定路线为沿途客户配送相应的货物。参与运输的车辆为临时租用,在完成最后一站客户的配送任务后即释放资源,停止计费。
3 模型建立

表2 客户需求货物量与收货频次信息
3.1 目标函数
拼车配送优化的决策变量为车辆型号和行车路线,优化的目标为所有参与拼装配送车辆的总运费最小。

式中:N指参与配送的车辆总数;ri指第i号车辆的费率;Vi指第i号车辆的标准计费吨位,单位t;n指第i号车辆所服务的客户总数;指第j-1号客户与第j号客户间的路程(其中0号客户代表配货中心),单位km;指第i号车辆的配送路线的总长度,单位km。
3.2 限制条件
拼车配送方案优化问题的限制条件包含以下几类:
(1)最大载重约束。所有参与拼装配送的车辆的载货总重量不超过最大载重限制,本文中最大允许载重为20t。

式中,vi指第i号车辆的载货量,单位t;vmax指车辆所允许的最大载重,单位t。
(2)最长时间约束。除特殊情况外,所有车辆的路线配送时间不超出最长允许时间限制,本文中路线最长配送时间为2d。

式中,Di指第i号车辆的路线配送时长,单位s;Dmax指路线最长允许配送时间限制,单位s。
(3)稳定路线约束。各车的行驶路线必须保持稳定,沿途所配送客户的频次属性应保持不变或增大趋势。

式中,Fij指第i辆车所服务的第j号客户的频次参数,单位d/次;Fij+1指第i辆车所服务的第j+1号客户的频次参数,单位d/次。
除上述3种主要的限制条件外,零散货物拼车配送优化问题还存在卸货时间约束,也即客户凌晨1:00-5:00期间不支持卸货,在此期间抵达的车辆需等到5点开始卸货;凌晨1:00前未完成卸货的车辆需停止卸货,等到凌晨5:00后继续作业。卸货时间不构成独立的约束条件,而主要通过最长时间约束来影响配送方案优化问题。
4 模型求解
上述车辆路径优化问题属于包含多维度变量组合优化的大规模NP难问题。NP难问题的求解算法主要分为确定性算法和启发式算法两类。对于小规模问题,可以考虑采用确定性算法求解;对于大规模NP难问题,一般采用启发式算法来求解。
4.1 算法简介
启发式算法具有较强的适用性和全局性,已被广泛应用于交通运输领域[8-11]。本文采用改进差分进化(Differential Evolution,DE)算法来求解有稳定路线约束的零散货物拼车配送方案优化问题。DE由R.Storn和K.Price提出[12-13],是一种基于群体差异的自启发式随机搜索算法。DE算法流程如图1所示。

图1 差分进化算法流程图
在车辆型号和数量不定的情况下,应用DE算法不能直接求解拼车配送路线优化问题。多种维度的变量,复杂的约束条件对算法性能构成较大挑战。本文通过改进染色体编/解码方案,提高DE算法的寻优效率,实现对复杂条件约束下的多种维度变量组合优化的大规模NP难问题的求解。
4.2 编/解码方案
应用DE算法优化拼车配送路线时,所采用的编码方案见表3。

表3 基因编码方案
表3中染色体编码需经解读才能生成拼装配送方案。方案解读过程中,可充分利用路线时间限制、车辆最大载重限制等条件,直接生成满足约束的拼装配送方案,减少罚函数的使用。具体方案解读方法如图2所示。
主要步骤如下:
步骤(1):判断所有货物是否已完成拼装配送。若是,转步骤(4);若否,转步骤(2)。
步骤(2):利用编号为i的车辆Ti试装载编号为j的货物。若装货后配送时间超过2天,则认为车辆Ti不能装载j货物,Ti装货结束,统计已装载货物量并选择相应车型,令i=i+1,开始下一辆车的装货,转步骤(1);若装货后配送时间不超过两天,转步骤(3)。

图2 染色体解码流程图
步骤(3):若Ti装载j货物后的总载货量不超过20t,令j=j+1,转步骤(1);若总载货量超过20t,则认为车辆Ti不能装载j货物,Ti装货结束,统计已装载货物量并选择相应车型,令i=i+1,开始下一辆车的装货,转步骤(1)。
步骤(4):结束并输出拼装配送方案。
应用上述染色体编/解码方法,解读表3中染色体所获得的配送路线和车型方案,见表4。

表4 基因编码方案
表4中,针对8个客户共形成了3条拼车配送路线,分别为 A80→A73→A72、A68→A83和 A81→A82→A70,各条路线相应的车型分别为T1、T1和T2。由于在编解码过程中充分利用了约束规则,因而表4中所有行车路线都不违反车辆最大载重限制和路线最大时长限制。但应当注意,上述编解码方法并未设置稳定路线规则,运输方案仍然需要使用罚函数,以淘汰路线不稳定的拼车配送方案。
4.3 分组-合并优化
在客户总数较多时,DE算法的寻优时效会明显降低。因此,建议采用分组寻优,而后合并优化的方法,也即先寻得各组的局部优化方案,而后将各组的局部优化方案合并优化。通过两级优化,在较短的时间内获得满意解。
分组寻优-合并优化的方法可能丢失全局最优解,但却能有效提高算法寻优时效。分组寻优-合并优化方法容易理解和实现,在配送时间约束严格的情况下是值得推荐的一种选择。
分组寻优-合并优化主要包含分组和合并寻优两个环节。在分组环节,可以采用模糊C均值聚类算法等将客户按地理位置分成容易处理的几类,在此不再赘述。
在合并优化环节,可以采用车间相互交互法,进一步优化车型和路线,方法流程如图3所示。
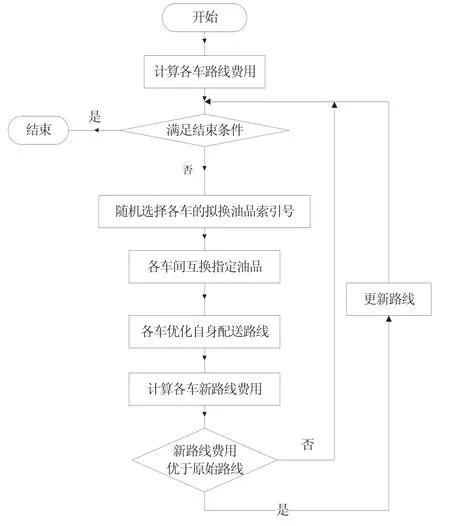
图3 车间交互法流程示意图
在合并优化时,各车之间应尝试相互交换一个或几个货物批次,若出现多个更为经济的配送,则应从最优的开始依次两两交换货物。在此过程中,两辆车间交换货物和各车重新优化自身的配送顺序是循环进行的,直至最终收敛。
值得注意的是,分组-合并优化的方法可能导致丢失最优解,但能够有效提高DE算法的寻优时效,提高使用者对时间消耗的容忍度。
4.4 案例分析
对于上文所述的优化问题,可根据地理位置信息,采用聚类算法预先将客户分成5组,如图4所示。
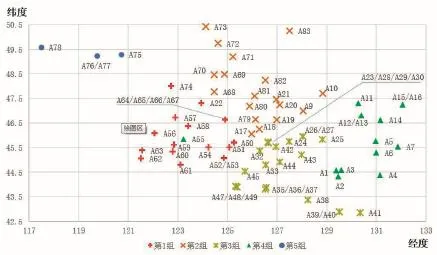
图4 客户地理位置分布图
由于客户A29和A64的需求量都超过了20t,因此需要预先拆分配送。其中将A29客户的需求量拆分成20t和1.07t,将A64客户的需求量拆分成20t和2.94t。对20t的整量部分直接安排载重20t货车进行配送,对A29客户剩余的1.07t和A64客户剩余的2.94t零散部分纳入拼车配送优化中予以考虑。
采用第4节所述算法求解第2节的拼车配送问题。通过分组-合并优化方法,得到最终方案见表5。
最终将所有客户的零散货物需求拼成了28辆车(算上客户A29和A64的2辆20t整车,该方案车辆总数总计30辆)进行配送,其中载重4t的货车13辆,载重6t的货车2辆,载重9t的货车1辆,载重12t的货车6辆,载重15t的货车4辆,载重18t的货车1辆,载重20t的货车1辆。经对比,该方案的总费用比人工方案节省约27.8%。
5 结论
随着运输业务外包化的发展,具有多车型、无限租量、路线稳定等复杂要求的拼车配送优化问题逐渐增多。本文以DE为主体,利用约束条件改进染色体的编/解码方案,利用车间交互法对大规模NP难问题进行分组-合并处理,最终实现了对零散货物拼车配送方案的快速优化。改进算法可能导致丢失最优解,但有效提高了寻优时效。应用改进的DE算法优化了包含79家客户的货物配送方案,最终将79家客户的零散货物拼成30辆车进行配送。所获得的优化方案路线稳定,易于执行,总费用比人工计划节约了27.8%。
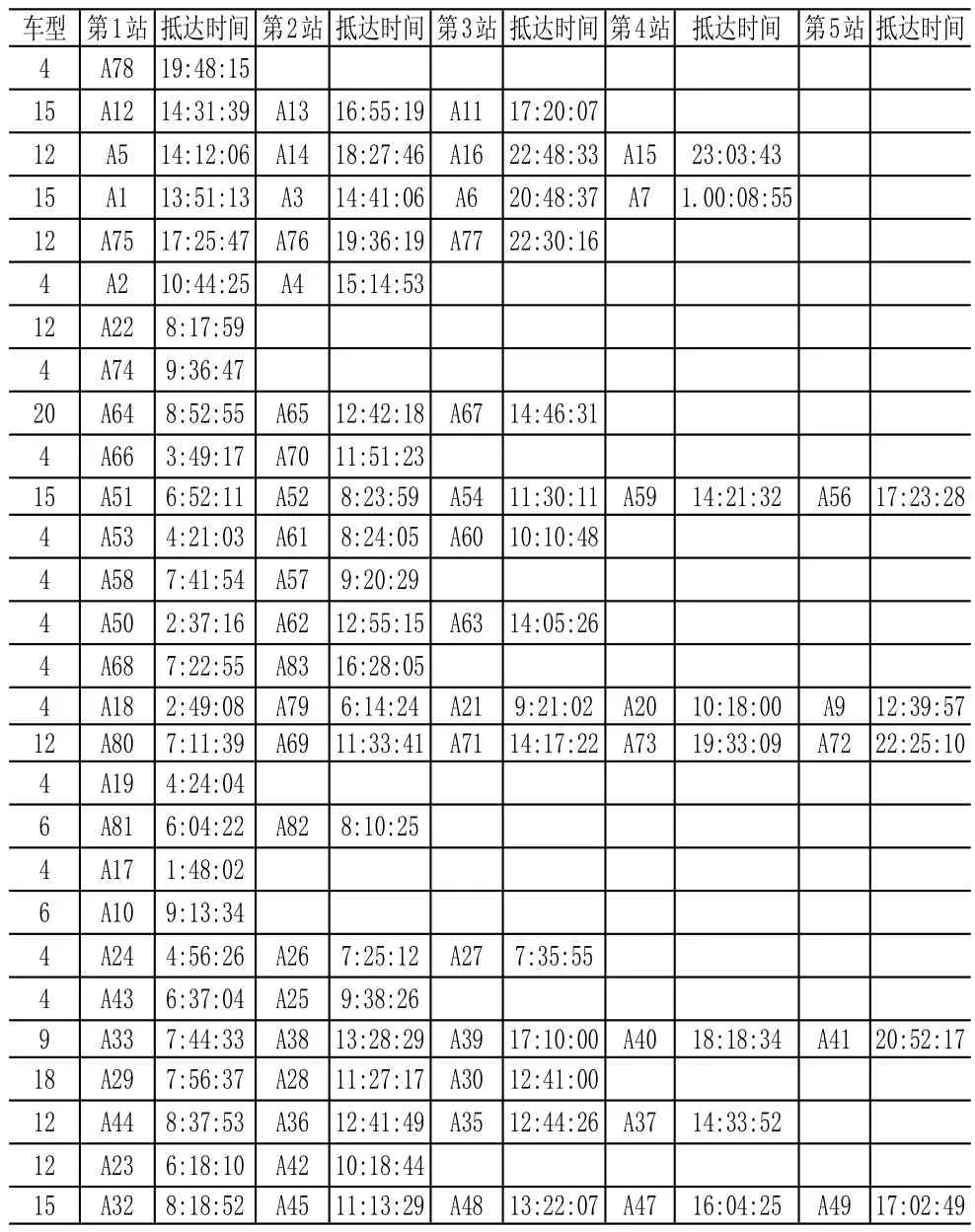
表5 优化配送方案
[参考文献]
[1]林宇肖.考虑油品隔离的成品油城市配送路径优化[D].大连:大连海事大学,2015.
[2]王宇奇,李靖泽.基于改进C-W节约算法的成品油二次配送优化研究[J].科技与管理,2014,16(1):51-55.
[3]强浓,王忠伟.基于遗传算法的物流配送路线优化系统设计与实现[J].物流工程与管理,2013,35(10):109-112.
[4]宋强.城市物流环境下车辆路径问题的研究[J].物流工程与管理,2017,39(2):51-55.
[5]吕圣杰.成品油公路运输配送系统优化策略[J].物流工程与管理,2014,36(11):64-65.
[6]王勇,肖文涛,李雪,等.我国原油远洋运输的运作模式及面临挑战[J].油气储运,2016,35(7):788-792.
[7]肖文涛,徐宁,刘志玲,等.原油采购-远洋运输方案模糊聚类图优化法[J].中国石油大学学报:自然科学版,2017,41(2):176-182.
[8]蔡延光,宋康,张敏捷,等.自适应多目标混合差分进化算法在联盟运输调度中的应用[J].计算机应用,2010,30(11):2 887-2 890.
[9]葛显龙,辜羽洁,王伟鑫.供应链环境下的库存与运输整合优化模型及算法[J].系统工程,2014,33(1):26-32.
[10]闫华,高黎,刘国勇,等.基于多时间窗的油料保障模型[J].计算机应用,2015,35(7):2 096-2 100.
[11]周晓玲,王震,肖文涛.原油远洋拼船运输方案优化研究[J].中国石油大学学报:自然科学版,2016,40(2):174-180.
[12]Storn R,Price K.Differential Evolution-a Simple and Efficient Adaptive Scheme for Global Optimization over ContinuousSpaces[J].TechnicalReport,InternationalComputer Science Institute,1995,(8):22-25.
[13]Storn R,Price K.Differential Evolution-a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J].JournalofGlobalOptimization,1997,11(4):341-359.
