应用于图像分割的改进贪婪蛇算法

， ， ， ，

(1. 淮安信息职业技术学院 计算机与通信工程学院， 江苏 淮安 223003； 2. 河海大学 计算机与信息学院， 江苏 南京 210098；3. 南京信息工程大学 计算机与软件学院， 江苏 南京 210044； 4. 南京师范大学 商学院， 江苏 南京 210023)

为实现一种可以高效地处理凹形图像的贪婪蛇算法，本文中在原始贪婪蛇算法的基础上提出一种改进贪婪蛇算法(improved greedy snake algorithm，IGSA)。IGSA首先对原始图像进行灰度处理，然后使用一种改进的GSA完成初始蛇素的收敛，最后通过一种贪婪算法完成蛇素的最终收敛。

1 基本的贪婪蛇算法

GSA中，蛇素的本质是一组有序点，其连线为最终提取的图像轮廓，因此，GSA也被认为是一种包含多个蛇素点的轮廓逼近表示方法。GSA模型的框架如图1所示。

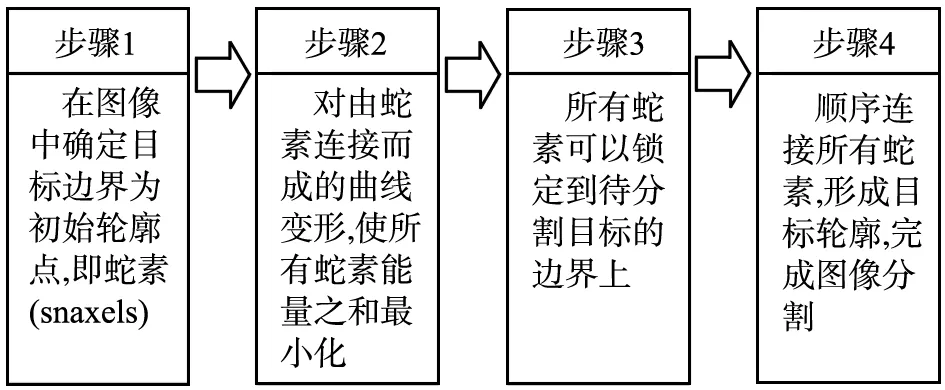
图1 贪婪蛇算法模型框架

GSA的计算目标是通过外力和内力，使初始蛇素最终移动到目标轮廓边缘位置，并确保蛇素之间有序且均匀分布，因此GSA整体上是一类基于图像属性的算法[12]。在GSA中，算法外力主要包括弯曲力和连续力，内力主要包括图像力。

基本的GSA的能量函数形式化描述为

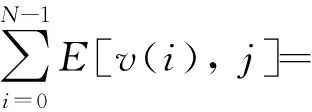
γiEimage[v(i),j]}，

(1)

式中：v(i)表示第i个蛇素；j为i蛇素邻域Gi内的第j个像素，j的取值与蛇素的一步移动距离δ有关；α、β、γ是伸缩参数，用来控制各组成部分的权重关系;Eant为连续力；Ecurv为弯曲力；Eimage为图像力。

蛇素的一步移动距离δ计算公式为

j=i±δk，k∈{1,2}

，

(2)

当k=1时， 蛇素一步移动距离取δ1∈{0, ±1}， 当k=2时，蛇素一步移动距离取δ2∈{0,±1,±2}。当k=1时，第i个蛇素的邻域Gi如图2所示。

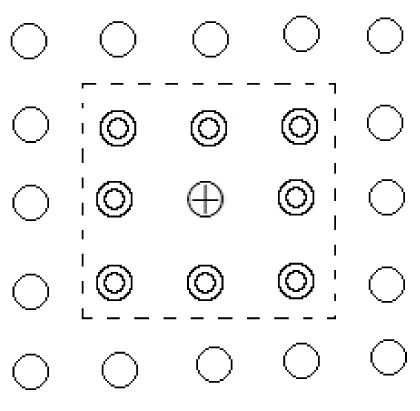
⨁表示蛇素；◎表示Gi内的像素；○表示普通像素。图2 蛇素的邻域Gi

在基本的GSA中，Gi集合由当前蛇素和其周围第1层像素构成，蛇素总数为9。一些改进算法，例如SGSA中[12]，蛇素一步移动距离取δ2，则Gi集合由当前蛇素与其周围2层像素构成，因此，SGSA的一步移动距离δ2∈{0,±1,±2}，其中蛇素总数为25。相较于GSA，SGSA的搜索范围增加，同时也意味着计算开销增大。为保证算法执行速度，IGSA中使用δ1∈{0,±1}、蛇素总数为9的模式。

连续力Econt的能量函数为

(3)

弯曲力Ecurv的能量函数为

(4)

式中 |v(i-1)-2v(i,j)+v(i+1)|表示对i-1、i+1个蛇素与Gi中的像素j进行和向量计算， 如图3所示。

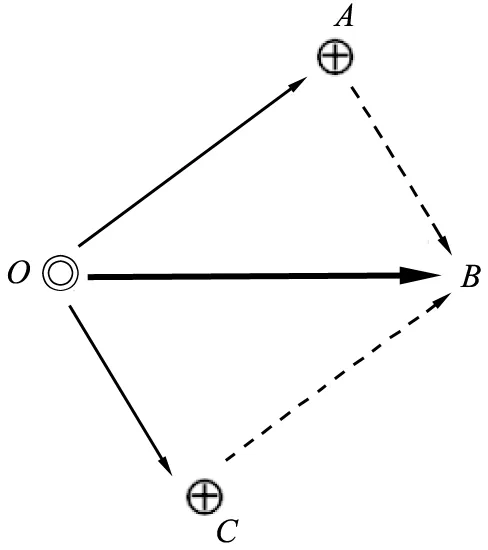
⨁表示蛇素；◎表示Gi内的像素。图3 |v(i-1)-2v(i, j)+v(i+1)|的计算过程

图3显示，GSA通过|v(i-1)-2v(i,j)+v(i+1)|

图像力的具体能量函数Eimage为

(5)

式中：I[v(i),j]表示Gi中第j个像素点的梯度值； min{I[v(i),j]}和max{I[v(i),j]}分别表示Gi所包含的像素的最小和最大梯度值。

在整个能量函数进行极小化的过程中，连续力能量函数使蛇素均匀分布于当前目标轮廓，弯曲力能量函数使其轮廓尽可能平滑，图像力使蛇素尽可能地停留在高梯度像素点。3个力同时作用，蛇素可以在外力的作用下不断向真实具体的轮廓进行移动，内力在保持蛇素拓扑性较好的同时随着蛇素点的移动而不断变化着，最终内力和外力相互制约形成一个较好的轮廓。

2 改进贪婪蛇模型

GSA算法要求初始化的蛇素只有在接近图像边缘的情况下才有比较好的收敛效果，并且无法提取凹形轮廓。为弥补上述不足，本文中提出了一种新的目标轮廓提取算法IGSA。完整的IGSA由3个部分构成，即图像灰度预处理、蛇素初始收敛和贪婪收敛。

2.1 图像灰度预处理

在一些图像分割问题中，原始图像往往存在斑点粗糙、噪点干扰等问题。灰度处理的目的是使原始图像的特征更加明显，使图像边缘化得到加强，去噪、锐化程度也相应地提高。灰度处理公式为

Grv(i), j=Δ1Rv(i), j+Δ2Gv(i), j+Δ3Bv(i), j，

(6)

式中：Grv(i), j表示某个像素点v(i)的灰度值；Rv(i), j、Gv(i), j、Bv(i), j分别表示红色、 绿色、 蓝色通道值；Δ1、Δ2、Δ3为权重系数，实践表明，Δ1=0.299，Δ2=0.587，Δ3=0.114时，图像灰度处理效果较为理想。当图像较大时，为避免浮点运算影响计算速度，对式(6)算法进行优化。具体方法为

(7)

式中k表示位移系数。式(7)相对于式(6)的效率提升效果，将通过实验数据加以验证。

2.2 GSA的改进

根据式(3)、(4)，Econt和Ecurv的取值范围都在(0,1]。前期实验中，通过定量分析发现，I[v(i),j]通常为一个3位实数，|max{I[v(i),j]}-min{I[v(i),j]}|

通常为一个远小于1的实数。相对于Econt和Ecurv，Eimage的取值范围过大，使得综合力E[v(i),j]几乎完全受Eimage影响。为了均衡3个力，本文中对Eimage进行了归一化处理，改进后的图像力公式为

(8)

式中Eimage的取值范围在(0,1]。整个蛇形算法能量函数可以由式(9)表示为

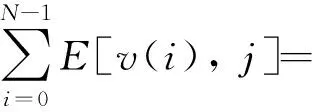
γiEimage[v(i),j]}。

(9)

从直观上看，式(9)为3项相加，而原始GSA中式(1)为加减混合计算。这样的变化，使综合力函数公式更加整洁，可控性更好。

2.3 贪婪策略

2.3.1 观测点选取

当式(9)迭代一定次数后，IGSA完成蛇素的初始收敛。蛇素初始收敛过程可以保证蛇素点依序散落在真实目标轮廓周围，但少量蛇素会因为弯曲力和连续力的综合作用而偏离目标轮廓。图像轮廓界定主要根据图像边界的梯度值，IGSA中使用的贪婪策略主要围绕梯度值完成运算。将初始轮廓视作一个N边形，则该N边形的中心被称为观测点px,y。如图4所示。

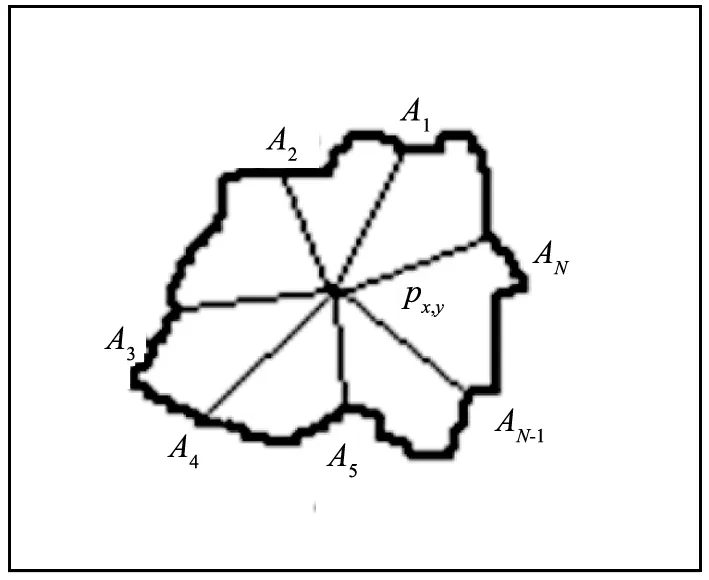
图4 观测点选取

px,y的坐标具有如下性质：

(10)

(11)

式中：A为由Px,y点出发的N条射线与轮廓的交点；Axi、Ayi为A点的坐标。当观测点px,y位于目标轮廓外围时，需要特殊考虑。此时的目标轮廓通常为凹形，对此我们设计出一套方法来解决此问题：

步骤1 以观测点px,y为端点，通过每个蛇素v(i)构造出N条射线L(i)，i=1,2,…,N。

步骤2 对于每条与轮廓相交的射线Li，i=1,2,3,…n，找到其交点并且依次记录，则这N个数据点表示为pxi,yi(i=1,2,3,…,n)，并且算出每条射线与轮廓交点的中点坐标mxi,yi(i=1,2,3,…,n) 如图5所示。

步骤3 此时，由这N/2组成的中点坐标mxi,yi(i=1,2,3,…,n)算出最后的辅助点为

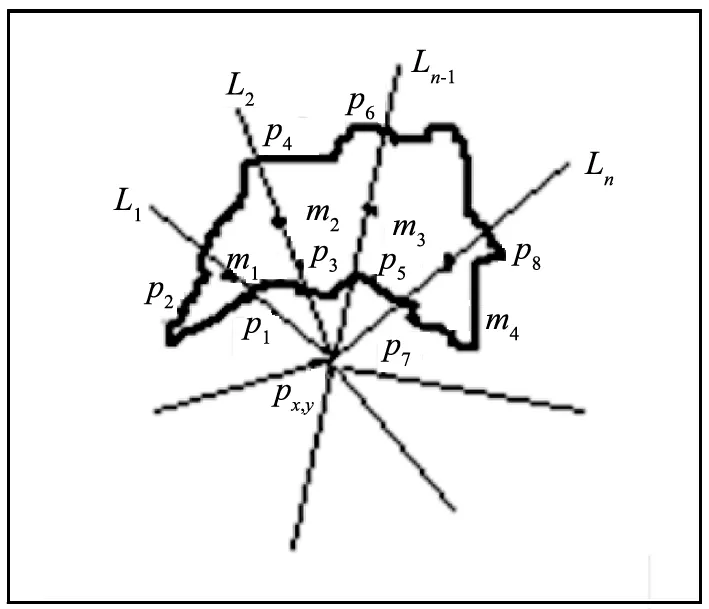
图5 辅助点在外的情况

(12)

(13)

2.3.2 贪婪策略执行过程

当观测点px,y设在一个分辨率M×N的图像中，对依据贪婪策略的曲线收缩步骤如下：

步骤1 其中新的蛇形模型能量函数Eimage从图像边界开始迭代i次后，轮廓已经初步收敛。

步骤2 以观测点px,y作为此当前蛇形模型能量函数Eimage的中心， 构造出n条射线Lj(j=1, 2, …,n)， 从当前辅助点px,y发出到此迭代i次后的轮廓边缘。 此时， 2条相邻直线的夹角为2π/n，如图6所示。

步骤3 对于每条直线Lj(j=1,2,…,n)，定义Pv(i, j)是此直线Lj上的第i个点，计算每个点的梯度Gv(i, j)，选取这条线上梯度最大值max{Gv(i, j)}作为收敛的最终点。

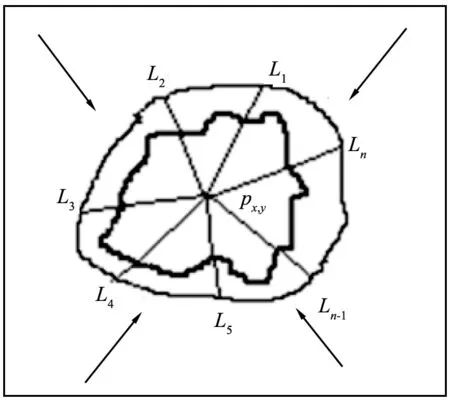
图6 轮廓边缘构造直线

步骤4 将每条直线Lj上的差距最大的值max{Gv(i, j)}连接构造出收敛的轮廓。

3 实验结果与分析

3.1 灰度处理算法优化后的性能测试

以一幅分辨率为2 560像素×1 600像素的图像为例， 经过实际运算后， 整理的实验数据如表1所示。

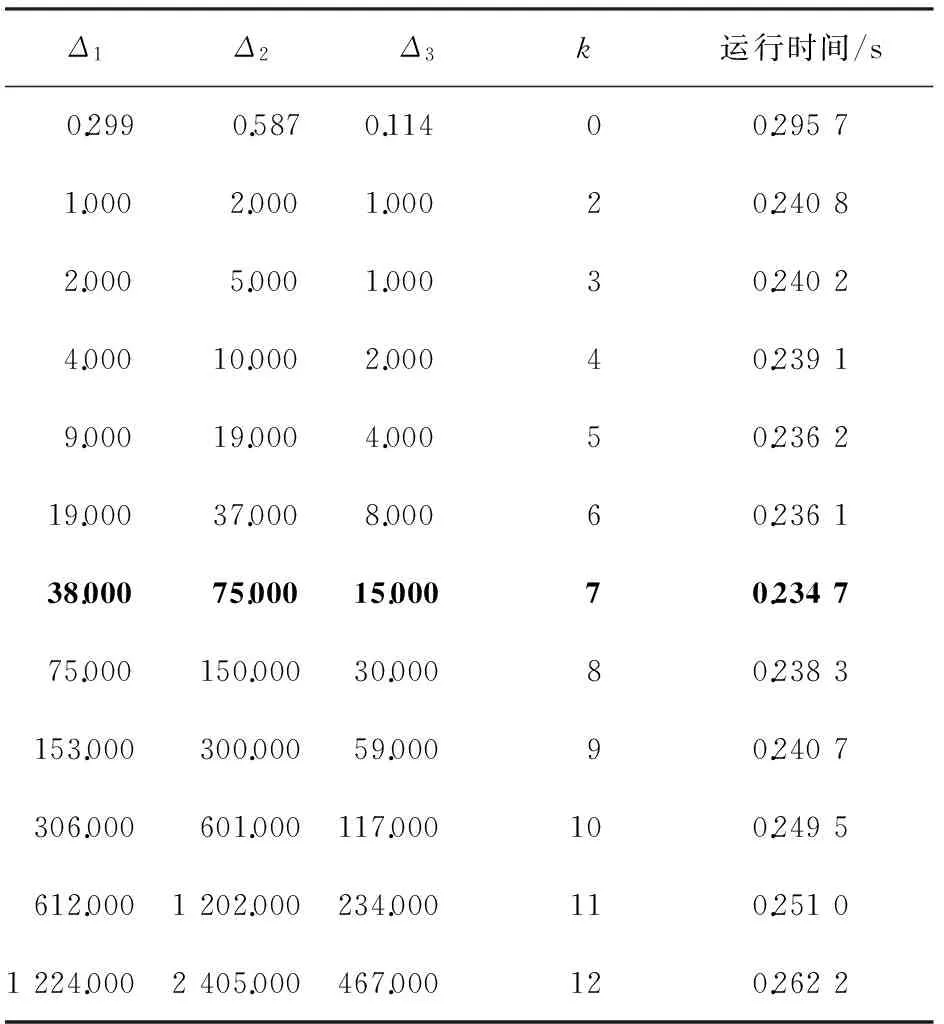
表1 权重系数Δ1、Δ2、Δ3取值对算法运行时间的影响

观察表1可以发现： 当k=0时， 式(7)就退化为式(6)。 同样条件下式(6)在所有参数组合中所耗时间最多。 所有参数组合中，Δ1=38，Δ2=75，Δ3=15，k=7的效率最高。IGSA的灰度预处理则使用上述参数配置。

3.2 IGSA算法目标轮廓提取实验

为了测试IGSA的性能，本文中进行3组实验。对比了IGSA和SGSA这2种算法。2种算法的参数设置如下：α=2.0，β=2.0，γ=1.0，初始化蛇素规模为500，算法迭代次数为150。

图7—9分别为SGSA和IGSA的蛇素收敛效果。

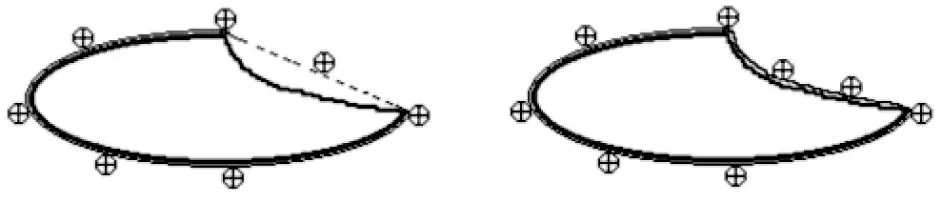
(a) 跳跃贪婪蛇算法 (b) 改进贪婪蛇算法图7 简单凹形几何图形分割效果图

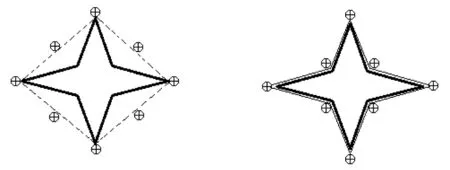
(a) 跳跃贪婪蛇算法 (b) 改进贪婪蛇算法图8 等曲率凹形几何图形分割效果图

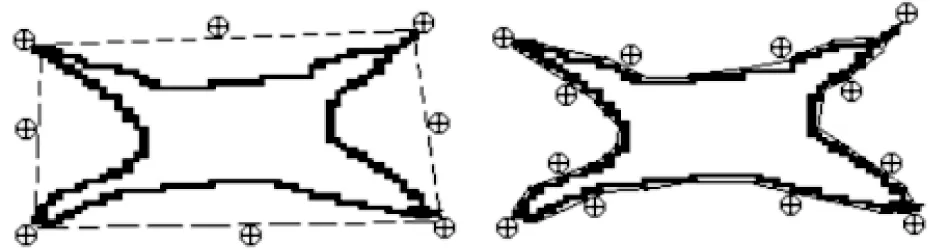
(a) 跳跃贪婪蛇算法 (b) 改进贪婪蛇算法图9 不等曲率凹形几何图形分割效果图

为了便于观察，实验中用“⨁”符号标记出了少量蛇素点位置。图7为一个简单凹形几何图形，拥有一个曲率不大的凹形区域。图8、 9是2个较复杂的凹形几何图形。图8中带有4个曲率相同的凹形区域，图9中带有2个曲率较大的凹形区域和2个曲率较小的凹形区域。上述实验中，IGSA都取得了较好的实验效果，特别是凹形区域的蛇素收敛效果令人满意。

为了进一步验证IGSA处理真实图像分割问题的有效性，本文中特别选取了2组真实图像。图10是一个拥有较大凹形曲率轮廓的真实图像，图11为一个复杂的人脸图像，拥有较复杂的轮廓。在图10中，SGSA只能完成粗糙的图像分割，无法收敛到凹陷区域，而IGSA展示出了较好的凹陷区域收敛能力，分割出的边界轮廓较为精准。图11中，在处理人脸轮廓提取问题上，SGSA虽然可以将整个人脸分割出来，但在细节上IGSA表现出了更好的分割效果。

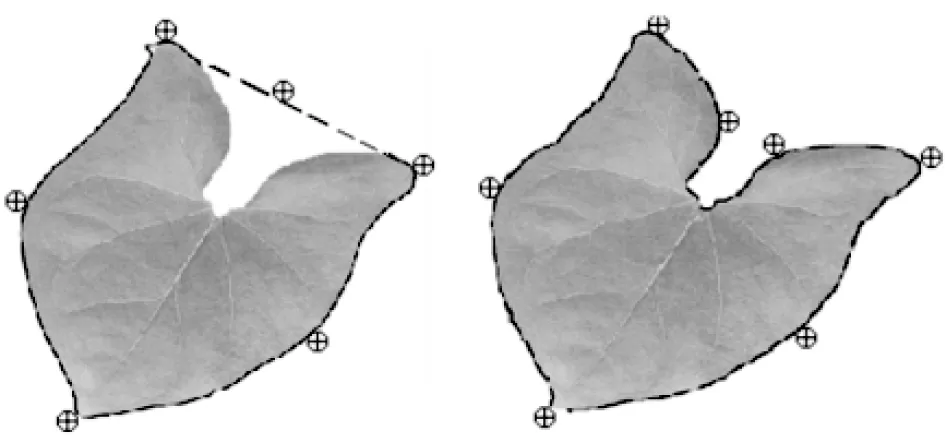
(a) 跳跃贪婪蛇算法 (b) 改进贪婪蛇算法图10 真实图像分割效果图

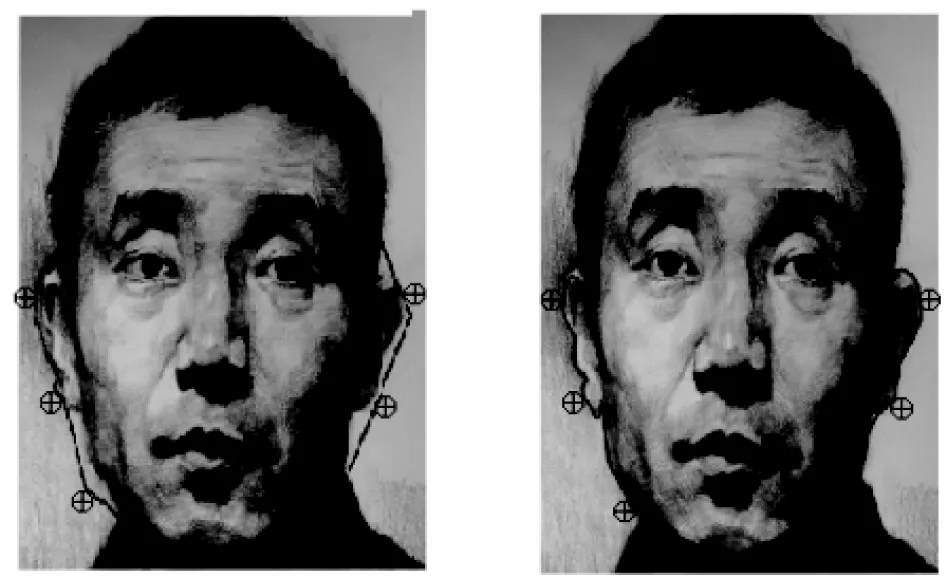
(a) 跳跃贪婪蛇算法 (b) 改进贪婪蛇算法图11 人脸图像分割效果图

综上所述，在处理真实图像分割问题中，相较于SGSA，IGSA有更好的轮廓提取效果，特别是IGSA更善于处理曲率较大的凹形图形。

4 结语

针对传统Snake模型对初始位置敏感以及非凹性的问题，本文中在GSA的基础上提出了一种IGSA。IGSA使用一种高效的灰度处理方法和一类改进的Snake模型收敛策略，并融入了贪婪方法。贪婪策略的使用使得IGSA可以较好地处理凹形图像轮廓提取问题。本文中通过凹形几何图像和真实图像，实验验证了IGSA的有效性和高效性。IGSA虽然取得了较好的图像分割效果，但也存在一些不足，如相较于GSA，IGSA在灰度预处理阶段和最后的贪婪收敛阶段要多占用一些系统开销，但这些开销相对于SGSA中每个蛇素每移动一步都增加计算量的做法还是较低的。另外，为了弥补这一不足，本文中已经通过实验方法对灰度预处理进行了优化。未来，考虑将IGSA算法应用于三维图像分割和人脸识别等一些实际问题。

参考文献:

[1] KASS M，WITKIN A. Snakes: active contour models[J]. International Journal of Computer Vision，1988，1(4):321-331.

[2] 王静文,刘弘. 基于Snake模型的植物叶片面积计算方法[J]. 计算机工程，2013，39(1): 234-238.

[3] LIU C, XIAO Y Y, YANG J. A coastline detection method in polarimetric SAR images mixing the region-based and edge-based active contour models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(7): 3735-3747.

[4] 蒋小波，梁久祯，周世兵. 基于GVF Snake和边界跟踪的主动轮廓图像分割[J]. 济南大学学报(自然科学版), 2015, 29(4): 269-274.

[5] ALMEIDA T M, CAVALCANTE T. Three-dimensional radial active contour model: a 3-D to 1-D image segmentation technique[J]. IEEE Latin America Transactions, 2017,15(2): 365-373.

[6] 沈宋衍，陈莹. 在线学习机制下的Snake轮廓跟踪[J].计算机工程，2015，41(4):195-198.

[7] COHEN L D, COHEN I D. Finite-element methods for active contour model and balloons for 2D and 3D images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(11):1131-1147.

[8] 刘宏申，孙晓娜，汪量. 基于改进Snake的多目标分割算法[J]. 计算机工程与设计, 2014,30 (19):4455-4460.

[9] 周志宇，杨卫成，汪亚明，等. 应用梯度矢量流Snake和灰预测的人脸轮廓跟踪[J].光学精密工程, 2014,19(11)：2744-2752.

[10] XU C Y. Gradient vector flow: a new external force for Snakes[C]//Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition. Washington D C: IEEE Computer Society，1997: 66-71.

[11] 祝世平，高洁. 基于变化检测和改进的GVF Snake模型的运动目标轮廓提取[J]. 光电子激光，2013，24(9):1083-1089.

[12] WILLIAMS D J, SHAH M. A fast algorithm for active contours and curvature estimation[J].CVGIP:Image Understanding, 1992, 55(1): 14-26.

[13] MUSTAFA S, LAM K M, YAN H. A faster converging snake algorithm to locate object boundaries[J]. IEEE Transactions on Image Processing，2013, 15(5): 1182-1191.