多机器人领航-跟随型编队控制

师五喜，王栋伟，李宝全

（天津工业大学电气工程与自动化学院，天津 300387）

在实际工程应用中，由于单个智能体自身能力的局限性，在处理复杂任务或处于复杂环境下仅靠个体行为往往无法解决.人们受到自然界中鱼群、鸟群等生物种群协作完成捕食、迁移等生物集群协作行为的启发，将这种生物集群编队协作的特点运用到多智能体系统中.目前，编队运动问题已在很多领域得到应用，例如在工业领域，人们控制多个移动机器人以特定队形搬运大的物体；在军事上，多个自主式小车被用于编队巡逻或侦察；在警务领域，人们控制多个移动机器人组成弧形包围或捕获入侵者等.

多机器人编队控制是目前国内外研究的热门课题之一.多移动机器人的编队运动，要求多个移动机器人作为一个编队同时运动到目标区域，并在运动过程中始终保持给定队形，同时能安全地避开可能出现的障碍物.这种群体行为控制是解决许多机器人协作问题的基础，它对实现多机器人在分布式空间环境中协同执行任务具有重要意义.编队控制方法有领航-跟随（leader-follower）法[1-5]、虚拟结构（virtual structure）法[6]、基于行为（behavior-based）的方法[7]、人工势场法[8]等.文献[1]提出了适用于2个机器人的距离-方位-方向控制方法和适用于3个机器人的距离-距离-方向控制方法.文献[2]用自适应控制方法，研究了有两个领导者，其余均为跟随者的编队控制方法.文献[3]提出了一种新的针对领航-跟随系统的运动学模型，该模型基于笛卡尔坐标.文献[4]针对车式移动机器人设计了一种领航跟随型编队控制算法.文献[5]通过设计模糊控制器，采用领航-跟随法实现了多机器人的编队控制.文献[6]结合人工势场和虚拟结构法，提出了一种针对多AUV的编队控制算法.文献[7]提出了一种基于行为法的机器人编队控制方法.文献[8]所采用的基于行为的方法可实现分布式控制，但此方法使队形控制的稳定性较差.文献[9]提出了一种基于行为法和领航-跟随法相结合的混合式编队算法，实现了对机器人的编队控制.文献[10]提出了一种基于滑模控制的机器人编队算法.文献[11]综合虚拟结构法和基于行为的方法，提出了一种带队形反馈的分布式编队控制算法.文献[12]设计了一套基于机器人动力学模型的编队控制算法.

以上算法虽然实现了编队控制的目的，但在编队运动过程中，对机器人速度和加速度大小没有限制.而在实际应用中，机器人本身对速度和加速度的大小有一定的限制，当速度和加速度大小超过机器人的截断速度时，机器人只会以自己允许的最大速度运行，这样在编队运动过程中，跟随机器人便不能准确地跟随领航者机器人，完成编队任务.文献[13]设计了一种具有速度与加速度限制的轨迹跟踪控制算法，该算法通过在原轨迹跟踪算法的基础上，增加了速度反馈，从而保证了机器人输入速度和加速度的有界性，但是该算法只是在单个机器人上实现了速度与加速度的限制，在机器人编队控制系统中，不仅仅要考虑到对领航者机器人的速度和加速度限制，而且对于跟随者机器人的速度和加速度大小也需要考虑在内.本文在文献[13]的基础上提出了具有速度和加速度限制的编队控制算法.通过引入2个一阶滤波器作为编队控制器的反馈信号，使得机器人的输入速度和加速度大小均有界.由于该反馈信号及其时间导数的大小完全受限于2个滤波器参数，因此可以通过调整2个滤波器参数的大小来调整机器人输入速度和加速度的大小.文中通过李雅普诺夫理论证明了闭环系统的稳定性，且通过仿真和在3个轮式移动机器人组成的编队平台上验证了本文方法的有效性.

1 机器人模型及问题描述

采用3个轮式移动机器人为研究对象，其中1个为领航者，另外2个为跟随者.对于领航者的移动机器人，其运动学模型只根据自身的位姿信息确定，而对于作为跟随者的移动机器人，其运动学模型建立在与领航者的位姿信息基础之上，通过与领航者的相对位置和角度信息来间接描述其自身的位姿信息.

1.1 领航者运动学模型

领航者机器人模型如图1所示.

图1 领航者机器人模型Fig.1 Leader robot model

假设领航者机器人在世界坐标系中的位姿为（x，y，θ），其中：（x，y）为领航者机器人的位置坐标；θ为机器人在世界坐标系中的方向角；v（t）与w（t）分别为机器人的线速度与角速度，则机器人的运动学模型为：

1.2 跟随者运动学模型

为了描述多机器人系统中各个机器人在队形结构中的位置，以2个机器人为例来说明本文所采用的领航-跟随者队形结构的几何模型.假设任意的跟随者机器人RF，其跟随的领航者机器人为RL，则本文采用的领航-跟随者队形结构模型如图2所示.

图2 领航-跟随者队形结构模型Fig.2 Pilot follower formation structure model

图2中，领航者机器人的线速度用vL来表示，角速度用wL来表示，线速度与水平方向的夹角用θL来表示.跟随者机器人的线速度用vF来表示，角速度用wF来表示，线速度与水平方向的夹角用θF来表示.以机器人两轮轴心连线的中点为参考点，则2个机器人参考点之间的距离为λL-F，领航者机器人前进方向与2个机器人参考点连线的夹角为φL-F.

对于一个领航-跟随编队系统，编队的主轨迹通常由领航者机器人决定，跟随机器人的参考轨迹由领航机器人生成的虚拟机器人轨迹决定[4].假设跟随者机器人与领航者机器人最终达到的距离与角度分别为和，那么虚拟机器人与领航者机器人之间的距离和角度分别为和.在世界坐标系X-Y中，虚拟机器人与领航者之间的位置关系为：

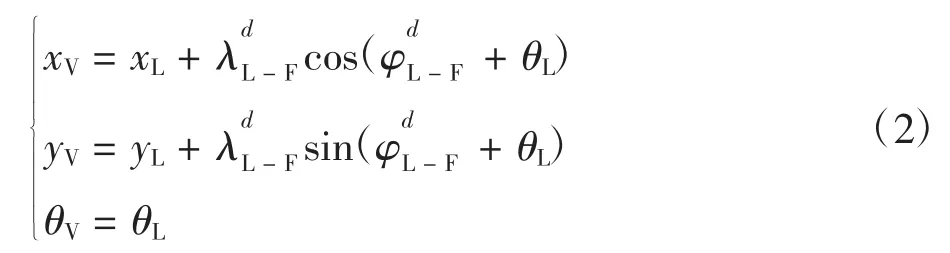
跟随者与领航者之间的位置关系为：

虚拟机器人与跟随者之间的表达式为：

通过转移矩阵，将其转换到跟随者机器人RF自身的坐标系xF-yF下的误差表达式为：

将式（3）和式（4）带入到式（5）中可得

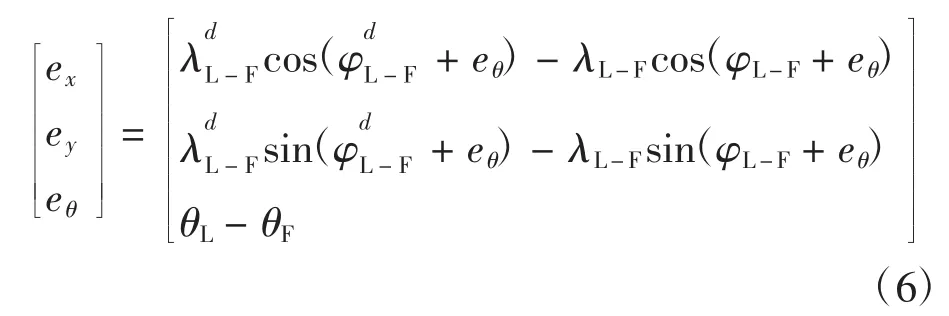
对式（6）两边求导可得[12]：

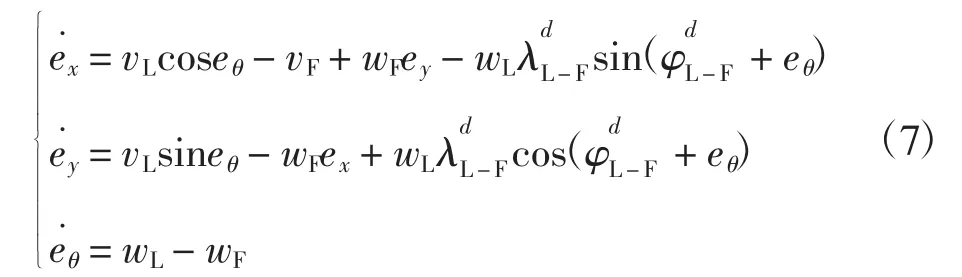
至此，机器人编队控制问题转化为跟随机器人RF对虚拟机器人RV的轨迹跟踪问题，即寻找合适的控制律（vFωF）使得式（7）描述的闭环系统渐近稳定，且

式中：vc、wc、av、aw均为正的常量.

2 控制器设计

文献[13]通过在原轨迹跟踪算法的基础上，添加了2个一阶滤波器，作为输入速度的反馈信号，从而使得机器人的输入速度和加速度有界，且其界限可以通过调整滤波器参数来调整.本文通过借鉴文献[13]的设计方法，通过对机器人编队控制算法进行调整，设计控制器如下：

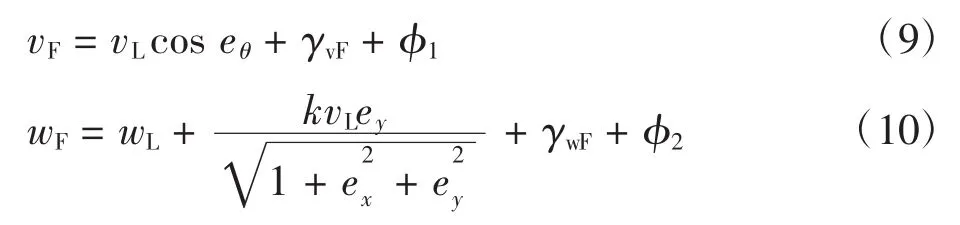
其中k为正反馈参数，

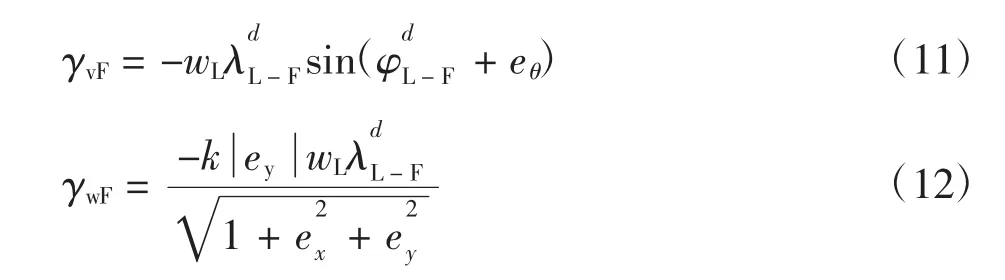
并且φ1和φ2分别为一阶滤波器产生的反馈函数：

其中α1和α2均为正滤波参数，且φ1（0）=φ2（0）=0.注1：与文献[13]所设计的针对单个机器人的轨迹跟踪算法相比，上述控制器引入了2个附加项γvF和γwF.对于基于运动学的多机器人编队控制算法，这2个附加项的引入保证了编队控制算法的稳定性.

定理1对于式（7）描述误差动态系统，设计控制律如式（9）和（10），自适应律采用式（13），则当 t→∞时，ex，ey，eθ均收敛于 0，并且控制律（vFωF）满足式（8）.

为证明以上定理，本文引入如下引理：

引理1[13]：如果一个有界的标量函数z（t）满足当t→∞ 时，z→0并且，其中 （ft）是有界的并且一致连续的，那么当t→∞时，并且f（t）→0.

证明：选取李雅普诺夫函数为：

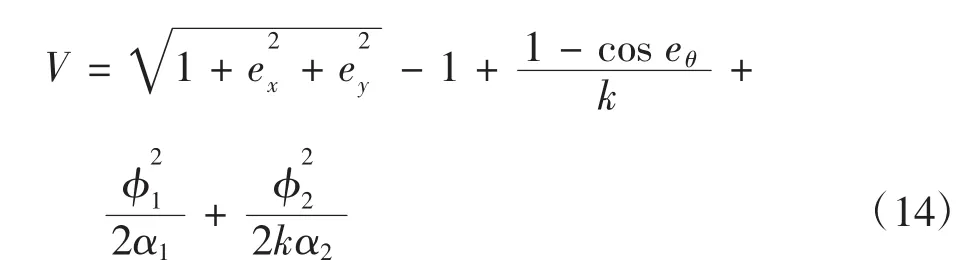
由式（7）、（9）、（10）、（11）、（13）可得

将式（12）代入式（15）可得：

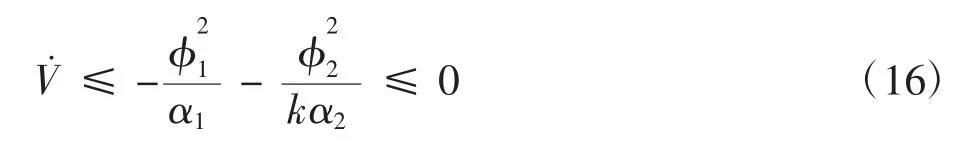
由式（7）和式（10）可得

所以当ey≥ 0，

当ey＜ 0，

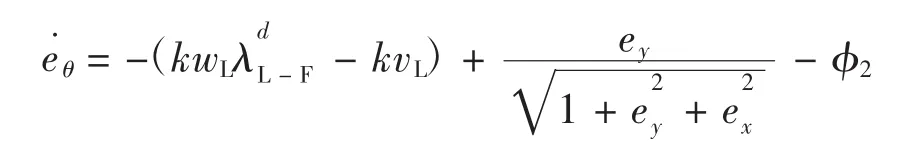
同理可得，当 t→∞，ey→0.

当 t→∞ 时，sin eθ→0，cos eθ可能收敛于 1 或者-1.由于 V（t）是非增的，假设 t→∞ 时，cos eθ→-1，则V（∞）→2/k.由于cos eθ（0）≠-1.所以当k取足够小时，总能满足 V（0）＜ 2/k，即 V（0）＜ V（∞）.这与 V（t）是非增的矛盾.因此当t→∞时，cos eθ→1.综上所述，当 t→∞ 时，ex，ey，eθ将收敛于 0.

下面先证明机器人输入速度和加速度的有界性.

由式（13）可知

由式（13）、式（19）、式（20）可知：

所以φ1和φ2是有界并且一致连续的.

由式（9）和式（19）可得

由式（10）和式（20）可得

由式（9）得

由（17）得

将式（25）代入到式（24）中得

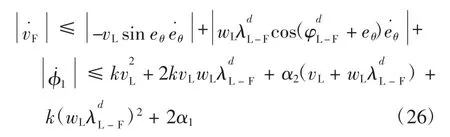
由式（10）得

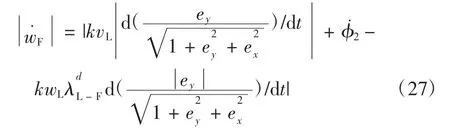
当ey≠ 0时，式（27）可以写为：

由于

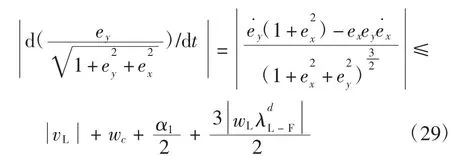
其中由式（8）和式（23）可得

将式（29）代入式（28）可得

当ey=0时

综上所述

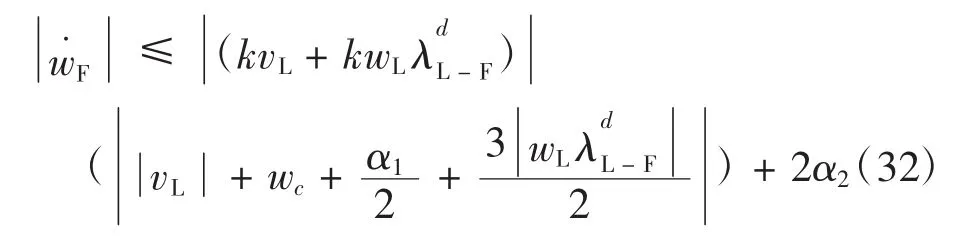
所以控制律（vFωF）满足式（8）.

3 仿真与实验

3.1 仿真

仿真中以3个机器人组成三角阵型队列为例进行验证，根据领航者走出的2种不同轨迹，分别进行了仿真，并且在仿真实验1中进行了速度与加速度有界性验证.仿真实验中，设定

vc=0.65 m/s，wc=1.2 r/s

ac=1.12 m/s2，aw=0.71 r/s2

2个跟随机器人与领航机器人最终达到的距离和角度分别为

仿真1：3个机器人从初始位置先完成三角阵型编队，然后保持编队做椭圆形运动.设领航者机器人的速度为（vL，wL）=（0.1，0.1），通过式（22）、（23）、（26）、（32）可以算得 α1=0.45，α2=0.5，k=3.0.3 个机器人的运动轨迹如图3所示，图3中跟随者1的运动轨迹为绿色虚线，跟随者2的运动轨迹为蓝色虚线.

图4所示为跟随者2的线速度、角速度、线加速度和角加速度.

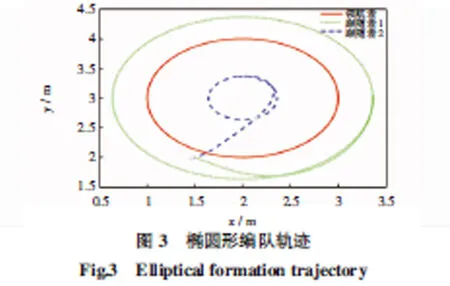
图4 跟随者2的速度和加速度Fig.4 Speed and acceleration of follower 2

由图4可知，其速度和加速度大小小于设定的速度与加速度上限.

仿真2：3个机器人从初始位置先完成三角阵型编队，然后保持编队做直线运动.设领航者机器人的速度为（vL，wL）=（0.1，0），根据式（22）、式（23）、式（26）、式（32）选定参数 α1=0.55，α2=0.1，k=1.0，运动轨迹如图5所示.

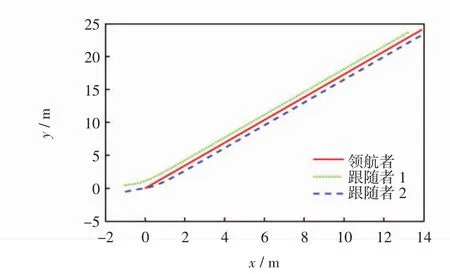
图5 直线形编队轨迹Fig.5 Linear formation trajectory

3.2 实验

以3个机器人组成三角形编队为例，根据领航者机器人运行的轨迹不同，进行了2次验证.

本文的实验平台为3辆小型轮式移动机器人，如图6所示.

图6 实验平台Fig.6 Experiment platform

小车以stm32f103zet6为处理器，2个直流电机为驱动轮，用1个万向轮来保持小车的平衡，3辆小车通过Zigbee模块实现通信，使得跟随者机器人能够实时的获得领航者的位姿信息，从而实现实时跟踪.

对于小车的电机控制，一方面实验要求能够精确的测出小车的运行速度.因此，需要通过编码器测出电机的转速.另一方面，电机要能够精确的实现给定的速度值，因此，小车的电机控制部分采用双闭环PID调速控制.

本次实验需要领航者将位姿信息实时地传递给2个跟随者，因此需要采用通信模块.通信采用Zigbee透传功能，设定领航者的Zigbee模块为协调器，跟随者的Zigbee模块为路由器，协调器只负责发送信息，路由器只负责接受协调器发送的信息，因此，2个跟随者只能接收领航者发送的信息，并且相互之间没有影响.使得跟随者能够准确地，实时地接收领航者的位姿信息.

实验1：3个机器人从初始位置先完成三角阵型编队，然后保持编队做椭圆形运动.设领航者机器人的运行速度，初始位姿以及与跟随者之间期望的位姿都跟仿真1相同.通过串口采集机器人的运动数据，则3个编队机器人的运行轨迹如图7所示.最后，2个跟随者机器人与领航者机器人组成三角阵型，并且保持三角阵型做椭圆形运动.

图7 组成三角阵型并且走出椭圆形轨迹Fig.7 Triangle formation and elliptical trajectory

实验2：3个机器人从初始位置先完成三角阵型编队，然后保持编队做直线运动.设领航者机器人的运动速度，初始位姿以及与跟随者之间的期望的位姿与仿真2相同.则3个机器人的运行轨迹如图8所示，3个机器人组成三角阵型并且走出直线轨迹.

图8 组成三角阵型并且走出直线轨迹Fig.8 Triangle formation and straight trajectory

4 结论

本文提出了一种具有速度和加速度限制的编队控制算法，通过加入2个一阶滤波器，在编队运动控制器的基础上加入了有界的反馈信号.研究结果表明：

（1）通过设定滤波器参数α1，α2的大小，可以设定编队机器人运行速度和加速度的最大值vm和am.

（2）文中证明了闭环系统的稳定性，仿真和实验结果也表明了.编队机器人可以稳定的组成设定的队形并且保持队形运动，且其运行速度和加速度均在设定的范围内，即当 t→∞ 时，位姿误差 ex，ey，eθ将收敛于0.且v＜ vm，a＜ am.

实验中以3个机器人组成的编队系统为研究对象，而实际应用中，经常需要更多的机器人来完成编队.本文研究成果不仅可以应用于3个机器人组成的编队系统，对于更多机器人组成的编队系统也同样适用.

参考文献：

[1]CHEN J，SUN D，YANG J，et al.Leader-follower formation control of multiple non-holomoic mobile robots incorporating a receding-horizon scheme[J].International Journal of Robotics Research，2010，29（6）：727-747.

[2]GUO J，LIN Z，CAO M，et al.Adaptive leader-follower formationcontrolforautonomousmobilerobots[C]//Baltimore，MD，USA：AmericanControlConference.IEEEXplore，2010：6822-6827.

[3]LI X，XIAO J，CAI Z.Backstepping based multiple mobile robots formation control[C]//Edmonton，Alta，Canada：IEEE/RSJ International Conference on Intelligent Robots and Systems.IEEEXplore，2005：887-892.

[4]王保防，张瑞雷，李胜，等.基于轨迹跟踪车式移动机器人编队控制[J].控制与决策，2015（1）：176-180.

WANG B F，ZHANG R L，LI S，et al.Formation control of vehicle based mobile robot based on trajectory tracking[J].Control and Decision，2015（1）：176-180（in Chinese）.

[5]吴垠，刘忠信，陈增强，等.一种基于模糊方法的领导-跟随型多机器人编队控制[J].智能系统学报，2015（4）：533-540.

WU Y，LIU Z X，CHEN Z Q，et al.A leader follower multi robot formation control method based on fuzzy method[J].Journal of Intelligent Systems，2015（4）：533-540（in Chinese）.

[6]潘无为，姜大鹏，庞永杰，等.人工势场和虚拟结构相结合的多水下机器人编队控制[J].兵工学报，2017，38（2）：326-334.

PANG W W，JIANG D P，PANG Y J，et al.Formation control of multi underwater robots based on combination of artificial potential field and virtual structure[J].Acta Armamentarii，2017，38（2）：326-334（in Chinese）.

[7]BALCH T，ARKIN R C.Behavior-based formation control for multirobot teams[J].IEEE Transactions on Robotics&Automation，1999，14（6）：926-939.

[8]YUAN J，TANG G Y.Formation control for mobile multiple robots based on hierarchical virtual structures[C]//IEEE International Conference on Control and Automation.Xiamen：IEEEXplore，2010：393-398.

[9]张捍东，黄鹂，岑豫皖.改进的多移动机器人混合编队方法[J].计算机应用，2012，32（7）：1955-1957.ZHANG H D，HUANG L，CEN Y W.Improved hybrid formation method for multiple mobile robots[J].Computer Applications，2012，32（7）：1955-1957（in Chinese）.

[10]SANCHEZ J，FIERRO R.Sliding mode control for robot formations[C]//IEEE International Symposium on Intelligent Control.Houston：IEEE，2003：438-443.

[11]REN W，BEARD R.Decentralized scheme for spacecraft formation flying via the virtual structure approach[J].Journal of Guidance Control&Dynamics，2012，2（1）：1746-1751.

[12]DIERKS T，JAGANNATHAN S.Control of nonholonomic mobile robot formations：Backstepping kinematics into dynamics[C]//IEEE International Conference on Control Applications.Singapore：IEEE，2007：94-99.

[13]CHEN X，JIA Y，MATSUNO F.Tracking control of nonholonomic mobile robots with velocity and acceleration constraints[C]//AmericanControlConference.Portland：IEEE，2014：880-884.

[14]朱大奇，杜青.基于领航位置信息的AUV三维编队控制方法[J].系统仿真技术，2013，9（3）：193-198.ZHU D Q，DU Q.Three dimensional formation control method of AUV based on navigation position information [J].System Simulation Technology，2013，9（3）：193-198（in Chinese）.

[15]DIERKS T，JAGANNATHAN S.Control of nonholonomic mobile robot formations：Backstepping kinematics into dynamics[C]//IEEE International Conference on Control Applications.Singapore：IEEE，2007：94-99.

[16]王中林，刘忠信，陈增强，等.一种多智能体领航跟随编队新型控制器的设计[J].智能系统学报，2014（3）：298-306.WANG Z L，LIU Z X，CHEN Z Q，et al.Design of a new multi-agent navigation following formation controller[J].Journal of Intelligent Systems，2014（3）：298-306（in Chinese）.