Gurney襟翼增升效应数值模拟

李荣鑫，朱晓军，章越超

（1.北京市第五十七中学，北京100038;2.南京航空航天大学，江苏南京210016；3.航空工业洪都，江西南昌330024)

0 引言

襟翼对机翼的流动控制一直以来都是飞机设计者研究的热点[1]，前缘缝翼和后缘襟翼都是襟翼的应用实例，是机械式的通过增加机翼弯度来提高机翼的有效迎角从而增加升力，目前两段式甚至三段式后缘襟翼已经被使用到大型客机机翼上了。近些年来一种被称为Gurney襟翼的襟翼逐渐进入大众的视野，被应用到航空领域中[2]。Gurney襟翼是指加装在机翼后缘下表面，垂直于翼型弦线，厚度和高度都很小的平板状增升装置[3]。Gurney襟翼的使用是一种被动流动控制手段，直接改变了机翼的形状，如果安装合理，则可以有效提高机翼的气动特性。

目前对Gurney襟翼的研究主要停留在二维阶段，三维情况研究的很少[4]。南京航空航天大学的周翰玮[5]采用数值模拟方法对风力机翼型以及超临界翼型上加装Gurney襟翼的控制效果进行了研究，发现Gurney襟翼不仅具有一定的增升效果还增加了叶片的低速轴扭矩，并有效缩小了大风速下叶片吸力面的分离面积，提升了风力机叶片的气动性能。北京航空航天大学的李亚臣等人[6]对不同形状的Gurney襟翼对NACA0012翼型流场的影响作了相应的实验研究，发现Gurney襟翼的最佳应用场合为中高升力系数情况(如起飞、降落等),在中小升力系数情况下不宜使用。对于Gurney襟翼，高度和安装位置是最重要的两个基本参数，本文主要在NACA0012翼型尾缘加装高度为翼型弦长的0.92%，2%，3.12%，垂直于弦线的Gurney襟翼，基于结构网格采用CFD的方法进行了小迎角下Gurney襟翼对翼型气动特性控制效果和对流场分布改进的数值模拟。然后固定一个Gurney高度，通过改变Gurney安装的不同弦向位置时对翼型气动特性的影响，与经典Gurney襟翼做对比，找出最佳的安装位置。最后基于二维加装Gurney襟翼后的翼型，沿展向拉伸成三维矩形机翼，分析Gurney襟翼对机翼气动特性的影响。

1 数值模拟方法

1.1 控制方程和湍流模型

本文采用不可压缩的雷诺平均N-S方程[7]，可表示为

连续方程：

动量方程：

采用有限体积法进行空间离散，对流项采用二阶迎风格式，扩散项采用中心差分格式，压力速度耦合采用基于压力的Simple算法处理，离散代数方程组采用Gauss-Seidel代数法求解[8]。湍流模型采用Spalart-Allmaras(SA)模型。SA模型是一个相对简单的一方程模型，求解了一个有关涡粘性的运输方程。该模型比较适合具有壁面限制的流动问题，对于有逆压梯度的边界层问题能够给出一个很好的计算结果。常常用于空气动力学问题中，例如飞行器、翼型等绕流流场分析[9]。

1.2 边界条件

翼型、Gurney襟翼和机翼表面采用物面边界条件，满足无滑移、绝热以及物面法向梯度为零的条件[10]。对于机翼，在对称面采用对称边界条件。流场中除了物面，对称边界以外，所有边界条件均采用压力远场边界条件。

1.3 物理模型及网格划分

二维模型采用NACA0012翼型，翼型弦长为1米。计算网格采用C-H型网格，如图1a所示。计算域四周边界距翼型表面距离均为弦长的20倍，吹气口处加密后的网格总数是43586。最内层网格高度为10-5米，y+≈1。

三维模型采用基于NACA0012翼型的有限翼展模型，如图1b所示。翼根弦向截面（z=0）是对称面，半翼展的参考面积是3平方米，计算域半展长是12米，所以翼稍（z=3米）处于流场之中，这样就考虑了翼尖涡的影响。

图1 模型及网格划分

2 二维模型数值模拟结果和分析

2.1 数值模拟算法验证

计算条件为：Ma=0.2，Re=4.6×106。NACA0012 原始翼型数值模拟和实验得到的升力系数值随迎角变化如图2a所示。从图中可以看出，在失速迎角以前数值模拟得到的结果和实验结果吻合得很好，两者升力系数最大误差只有3.7087%。翼型表面压力分布也是验证数值模拟准确性的一个重要参数[11]。当迎角α=10°时，数值模拟结果和实验结果的压强系数分布如图2b所示。从图中可以看出，此时数值模拟结果和实验结果吻合的也很好，由此可见，该方法满足工程应用要求。

图2 数值模拟和实验结果

2.2 不同高度的影响

为了研究不同高度的Gurnry襟翼对翼型气动性能和流场分布的影响，探索Gurney襟翼增升机理，首先固定Gurney襟翼的弦向位置，安装在型尾缘下表面，然后改变Gurney襟翼的高度，如图3所示，依次选为翼型弦长的0.92%，2.08%，2.92%。

图3 不同高度的Gurney襟翼

为保证计算结果的一致性和可比性，边界条件和计算网格均采用2.1节中所给出的安排，画出不同高度情况下的带Gurney襟翼的翼型网格。通过数值模拟可得到不同高度的Gurney襟翼控制效果并与原始翼型做对比。

图4是在后缘加装高度为2.92%倍弦长和原始状态的NACA0012翼型在0度迎角下的压力云图，从图中可以看出，原始状态的NACA0012翼型在0度状态下的上下表面压力分布基本一样，升力为零。但是加装Gurney襟翼之后翼型上面压力减小，下表面压力明显增大，导致下表面压力大于上面压力，这样就产生了升力。图5是在后缘加装高度为2.92%倍弦长和原始状态的NACA0012翼型在0度迎角下的后缘附近流线图，从图5中可以看出，原始状态的NACA0012翼型上下表面的气流在后缘平顺汇合流向下游，但是加装Gurney襟翼之后，在Gurney襟翼前端产生了一个旋涡，在Gurney后端产生了一对反向的旋涡，后端的旋涡比前端的大，可以推断这对旋涡就是翼型升力增加的主要原因。

图5 流线图对比

加装高度为翼型弦长的0.92%，2%，2.92%的Gurney襟翼时，不同迎角下的的翼型升阻力系数如图6所示。

从图中可以看出，在迎角固定情况下，在一定高度范围内，翼型的升力系数和阻力系数都随着Gurney增高而增大。零度情况下原始翼型的升力系数值为零，加装2.92%倍弦长的Gurney襟翼后，翼型的升力系数值增加到0.526358，说明增升效果很明显。随着迎角的变化，各种情况下的升力系数值变化大致相同，升力线斜率并不改变。

图6 升阻力系数变化

2.3 不同弦向位置的影响

由于翼型尾缘厚度很小，可能不适合加装Gurney襟翼，为了研究Gurney襟翼在不同弦向位置时对翼型气动特性的影响，找出最佳的安装位置。本节首先固定Gurney襟翼的高度，取为翼型弦长的2.92%。然后改变Gurney襟翼在弦向的位置，襟翼沿弦线安装位置为80%，90%，100%弦长位置，如图7所示。

图7 不同弦向位置的Gurney襟翼

同样为保证计算结果的一致性和可比性，边界条件和计算网格均采用2.1节中所给出的安排。画出不同位置情况下的带Gurney襟翼的翼型网格，通过数值模拟对比分析在其他位置加装Gurney的控制效果以及和经典Gurney襟翼之间的优劣性。

图8是Gurney在0.8c和0.9c弦向位置时，Gurney襟翼附近流线图。从图中可以看出Gurney襟翼在不同位置时，襟翼前后的流场结构十分相似，都是在前端产生一个分离涡，在后端产生一个反向对涡。但还是有些变化的，襟翼前端分离涡随着襟翼向后缘偏移也向后偏移，襟翼后端反向对涡始终充满襟翼后端至翼型后缘的整块区域，因此随着襟翼向后缘偏移，后端的反向对涡会随着中间区域的缩小而缩小。

图8 流线图对比

Gurney襟翼在80%，90%，100%弦线位置时，不同迎角下的的升阻力系数和压力系数如图9所示。

从图9中可以看出，Gurney襟翼在不同位置时，翼型气动力系数随迎角变化的趋势大致相同。相同迎角下，随着Gurney襟翼向后偏移，翼型的升力系数值不断增大，相应的阻力系数值越来越小，则升阻比也越来越大。0度情况下，增加Gurney襟翼之后，上下表面的压力系数分布开始产生了变化，下表面压强增大而上表面压强减小，因此产生了一定的压差。并且，随着Gurney襟翼向后移动，下表面的正压区域变得更大，从而导致总的升力系数值变得更大。由此可见，Gurney襟翼越向后缘靠近其增升效果越好。

图9 升阻力和压力系数变化

2.4 Gurney襟翼增升机理探索

通过对加装不同高度和不同弦向位置的Gurney襟翼后的NACA0012翼型的气动力系数和周围流场分布的数值模拟，并将计算结果与原始翼型数据作对比分析。

一方面，从外形上来看，在翼型尾缘下面加装Gurney襟翼相当于增加了尾缘的的曲率，也就是增加了翼型的有效弯度，从而增加了绕翼型的典型环量，进而提高了翼型的升力系数；另一方面，从流场结构分布来看，加装Gurney襟翼之后，会在襟翼前端产生一个旋涡，后端产生一对反向旋涡结构，这对旋涡结构会对后缘上表面的气流产生一定的诱导作用，使后缘上表面的气流向下吸附，这样就相当于增加了上表面气流流动的速度，上表面压强会相应的减小，由于Gurney襟翼的存在会对下面气流的流动产生一定的阻碍，并且增加了下表面的路程，使下表面的气流速度减慢，下表面压强增大，从而翼型上下表面会产生一定的压差，增加升力。

3 加装Gurney襟翼对矩形机翼气动特性的影响

基于上述二维模型研究，可知加装Gurney襟翼对翼型的升力系数和升阻力比都有一定的提升。为了了解在三维机翼上加装Gurney襟翼会是什么效果，本节采用基于NACA0012翼型的有限翼展模型，半展长为3米，翼根弦向截面（z=0）是对称面，半翼展的参考面积是3米。在其后缘0.9c处加装高度为2.92%倍翼型弦长的Gurney襟翼，分布在整个机翼的展向。图10是加装Gurney襟翼后的机翼局部示意。

图10 加装Gurney襟翼的矩形翼局部示意图

计算条件和前面二维翼型保持一致，数值模拟加装Gurney襟翼后的矩形翼在不同迎角下的升阻力系数以及流场分布，并与原始机翼作对比。

如图11所示，加装Gurney襟翼后机翼下表面的压力明显比原始状态下的机翼要大，导致机翼上下表面产生一个压力差，引起升力的产生。如图12所示，与二维模型一样有着类似的规律，在相同迎角下加装Gurney襟翼的升力系数和阻力系数都会有一定的增加，随着迎角的增加，升阻力系数增加的趋势大致相同。由此可见，Gurney襟翼对于三维矩形机翼也有相同的增升效果，对流场的改变也跟二维相似。

图11 压力云图对比

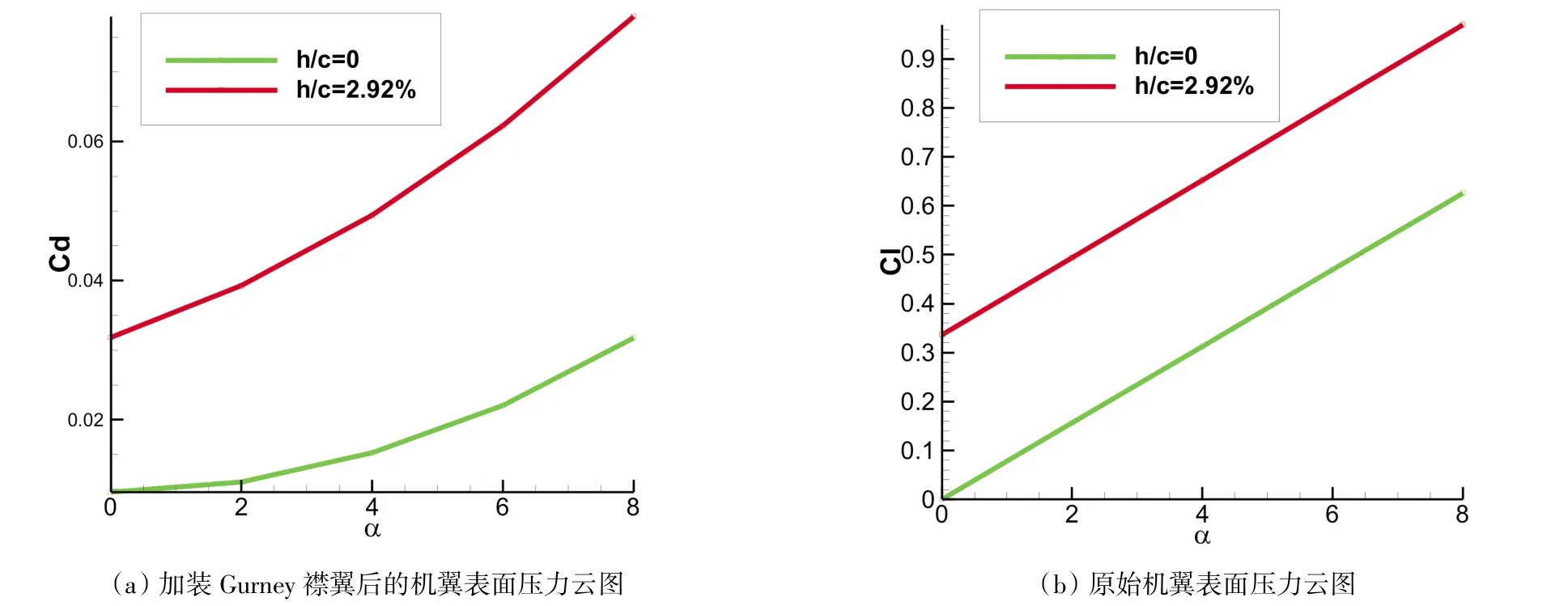
图12 压力云图对比

4 结论

1）采用适当的设置，可以准确地模拟出翼型的气动特性，该方法可满足工程应用的要求；

2)在NACA0012翼型后缘下表面加装Gurney襟翼，改变了翼型的整体外形，通过改变翼型上下表面的压力分布，使翼型升力系数增加，不同高度和不同安装位置都会有不一样的控制效果，在一定高度范围内，随着Gurney襟翼高度增加，升力系数也变得更高，同样的阻力系数也变得更大。相同高度情况下，随着Gurney襟翼向后缘推移，升力系数增大，阻力系数减小，控制效果会更好；

3)在三维有限翼展模型后缘下表面加装Gurney襟翼，同样可以改变机翼的上下表面压力分布，使机翼升力系数增加，在后缘0.9c处加装2.92%倍弦长的Gurney襟翼，在0度状态下升力系数能增加0.33673，不同迎角下增加量大致相同，说明Gurney襟翼对三维机翼的增升效果还是非常明显的。

[1]刘沛清,杨硕.Gurney襟翼对某型客机流动控制数值模拟[J].航空学报,2012,33(9):1616-1623.

[2]Shmilovich A,Yadlin Y.Flow control for the systematic buildup of high-lift systems[J].Journal of Aircraft,2008,45(5):1680-1688.

[3]Fuglsang P,Bak C.Development of the Risφwind turbine airfoils[J].Wind Energy,2004,7(2):145-162.

[4]Tang D,Dowell E H.Aerodynamic Loading for an Airfoil with an Oscillating Gurney Flap[J].Journal of Aircraft,2012,44(4):1245-1257.

[5]周翰玮.Gurney襟翼在风力机上应用的气动数值研究[D].南京航空航天大学,2013.

[6]李亚臣,王晋军,张攀峰.平板/锯齿型Gurney襟翼对NACA0012翼型增升实验研究 [J].航空学报,2003,24(2):119-123.

[7]CHANG T L,RACHMAN A,TSAI H M.Flow control of an airfoil via injection and suction[J].Journal of Aircraft,2009,34(7):291-300.

[8]Meunier M.Simulation and optimization of flow control strategies for novel high-lift configuration[J].AIAA Journal,2009,47(5):1147-1157.

[9]朱一西，陆志良，郭同庆.多段翼型非定常地面效应数值模拟[J].空气动力学学报.2014

[10]郭同庆.复杂组合体跨音速非定常气动力和颤振计算[D].南京航空航天大学.2006.

[11]Christopher L.Rumseya,Susan X.Ying.Prediction of high lift:review of present CFD capability[J].Progress in Aerospace Sciences,38 (2002)145-180.

[12]Shmilovich A,Yadlin Y.Flow control for the systematic buildup of high-lift systems[J].Journal of Aircraft,2008,45(5):1680-1688..

[13]Angelo C,Bert G.Numerical study of the optimization of separation control [R]. 45th AIAAAerospace Sciences Meeting and Exhibit,2007.