红外成像导引头跟踪丢失状态下的控制策略研究

徐辉

（海军驻南昌地区航空军事代表室，江西南昌330001）

0 引言

红外成像导引头因具备昼间/夜间全天时作战能力以及输出导引信号精度高等优点，在对地精确制导武器中获得了广泛的应用。飞行过程中，导引头连续获取目标所在场景的红外图像并对目标进行实时跟踪，由于采用被动工作方式，故隐蔽性好，抗电磁干扰能力强[1,2]。但是由于红外成像导引头不能测距，无法对目标进行定位，一旦在飞行过程中由于云层遮挡等原因造成跟踪丢失情况后，飞行器无法确定目标位置，控制时无导引信号，可能造成飞行失控，为避免出现这种情况，有必要在导引头跟踪丢失后采取相应的控制策略，以保持飞行器朝目标飞行。

目标被动定位算法可以综合利用飞行器上惯导输出的位置信息和导引头测角信息，通过扩展卡尔曼滤波算法（EKF）迭代估算目标位置信息，算法收敛后可以以较高的精度输出其相对位置信息[3,4]。本文针对导引头跟踪丢失情况提出了一种飞行控制策略，在导引头稳定跟踪过程中，通过目标被动定位算法实时估算其相对位置信息，当导引头跟踪丢失后根据估算得到的相对位置信息和惯导输出的飞行器实时位置、速度信息解算理论导引信号，并根据该信号生成控制指令控制飞行器朝目标飞行。

1 跟踪丢失状态下的飞行控制流程

飞行器作战使用过程中，为使载机尽快脱离危险区，提高载机生存概率，通常采用“发射前锁定，发射后不管”方式。典型作战过程如下：发射前载机带弹飞行，发现目标后飞行员通过导引头锁定目标，满足发射条件后发射，导引头稳定跟踪目标并输出导引信号，飞行器根据导引头输出的导引信号生成控制指令朝目标飞行直至命中。

实际飞行过程中，由于受云层遮挡、目标区背景干扰、目标表面特征纹理不明显等原因影响，可能会造成导引头跟踪丢失情况如图1所示。跟踪丢失后，导引头无法输出导引信号，从而导致飞行器飞行失控或明显偏离目标，飞行试验中还可能对地面设施或人员造成危险。

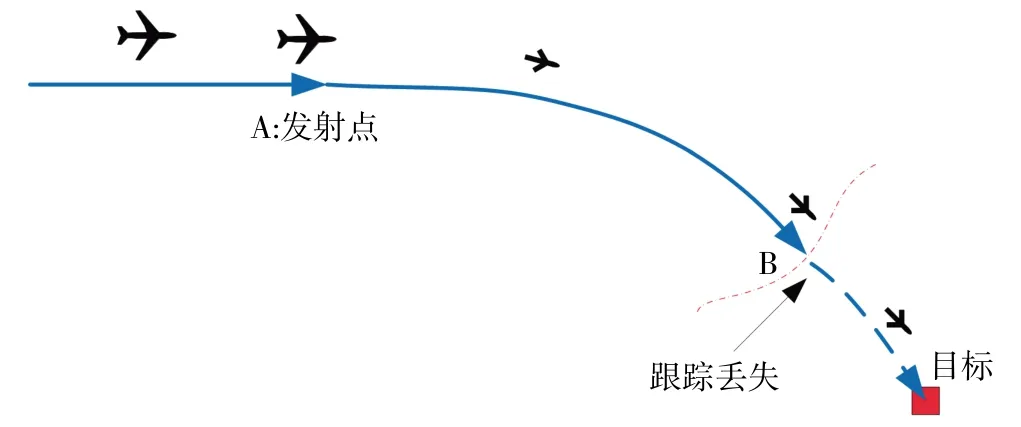
图1 作战使用过程示意

为了在导引头跟踪丢失情况下保持飞行器朝目标稳定飞行，本文提出如下的飞行控制策略：在导引头锁定目标并稳定跟踪过程中，根据导引头输出的导引信号以及飞行器经纬高等信息实时解算目标位置信息，当导引头跟踪丢失后，根据目标位置信息和飞行器位置信息解算理论导引信号，控制系统根据理论导引信号生成控制指令，控制飞行器朝目标飞行直至命中目标或落地自毁。飞行控制流程见图2。

图2 飞行控制流程

2 目标被动定位方法

如图3所示，M为飞行器质心，T为目标点，在目标点处建立测量坐标系MCS，x轴沿初始发射方向，y轴在水平面内与x轴垂直，z轴垂直与x、y轴。设飞行过程中，飞行器上组合导航系统输出的飞行器实时经纬度为λ、φ，惯导输出的飞行器航向、俯仰姿态角分别为α1、β1，测高系统输出的飞行器飞行高度为H（气压高度或大地高度），导引头输出的航向、俯仰框架角分别为αF、βF，根据以上输入信号，采用目标被动定位算法可迭代估算出飞行器在测量坐标系中的位置坐标为(x0,y0,z0)，飞行器与目标点的相对距离为dR、水平距离为dS。

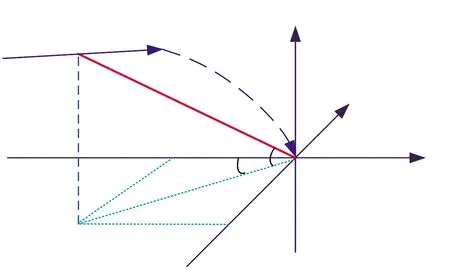
图3 飞行器与目标点的空间位置关系

目标被动定位算法通过扩展卡尔曼滤波算法（EKF）来实时确定其相对位置关系。卡尔曼滤波算法是一种线性系统状态估计算法，在状态空间模型的基础上，通过递推处理，寻求最小均方误差意义下状态矢量的最优估计。对于非线性系统，需要利用泰勒级数展开将非线性函数线性化，然后应用线性卡尔曼滤波理论，构成求解非线性滤波问题的次优滤波算法，即扩展卡尔曼滤波（EKF）[5]。

下面首先建立飞行器运动的状态空间模型，然后采用扩展卡尔曼滤波算法（EKF）来实时估计飞行器的位置。

以飞行器的空间位置和速度作为状态变量：X=[x yzVxVyVz]T，假设两次采样间隔之内（几十毫秒）飞行器匀速运动，则可以建立如下的离散化的系统方程：

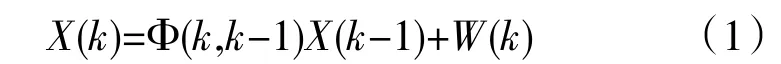
其中，Φ(k,k-1)=表示状态转移矩阵，W(k)表示6×1维的系统噪声向量，T表示采样时间。

以飞行器高度和航向、俯仰视线角作为观测量，则可以建立如下的测量方程：

简记为：Z(k)=h[X(k)]+V(k)。其中，V(k)表示 3×1维的测量噪声向量。

由于测量方程为非线性方程，需要对其进行线性化处理以应用EKF算法：

其中：

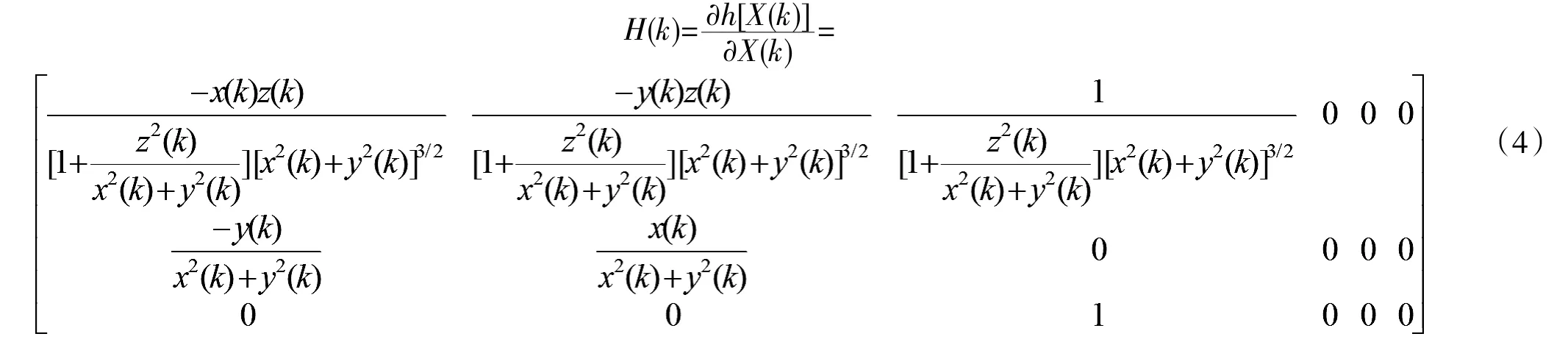
假设系统噪声W(k)和观测噪声V(k)为互不相关的零均值随机白噪声序列，满足如下的噪声统计特性：

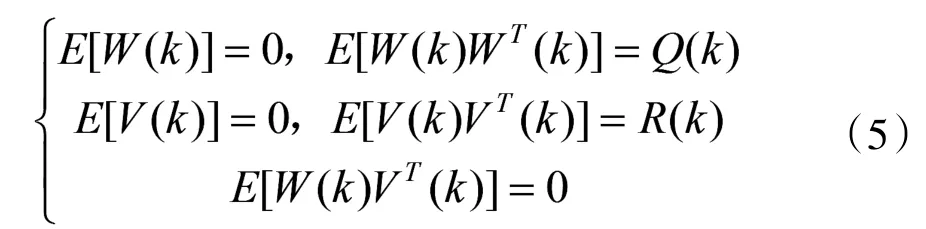
滤波器的初始状态估计值为：X(0)=[x(0)y(0)z(0)Vx(0)Vy(0)V(0)z]T。其中，飞行器的初始位置估计值通过几何定位方法来确定：

初始速度估计值为：

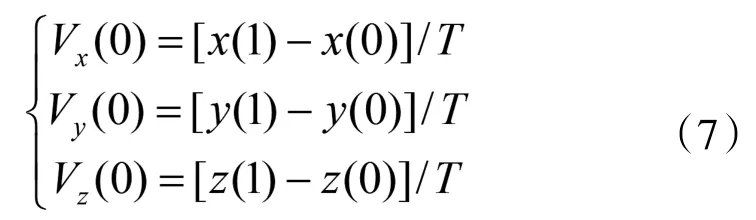
在建立了离散系统状态方程和测量方程并确定了初始状态估计值之后，可以通过以下的EKF递推公式来实时估计系统的状态变量：

状态预测：

协方差阵预测：

Kalman增益：

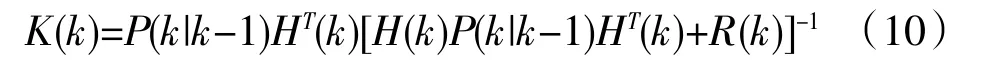
滤波方程：

滤波协方差阵：

3 理论导引信号解算

设飞行器在测量坐标系中的实时位置坐标为(x,y,z)，导引头跟踪丢失时刻飞行器在测量坐标系中的位置坐标为(x0，y0，z0)，飞行器速度在测量坐标系中的分量表示为（Vx,Vy,Vz），则飞行器实时位置坐标为：

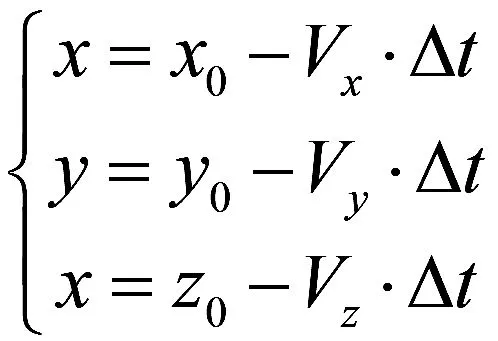
其中，Δt=t-t0,t0表示导引头跟踪丢失时刻。理论视线角速度解算方法如下：

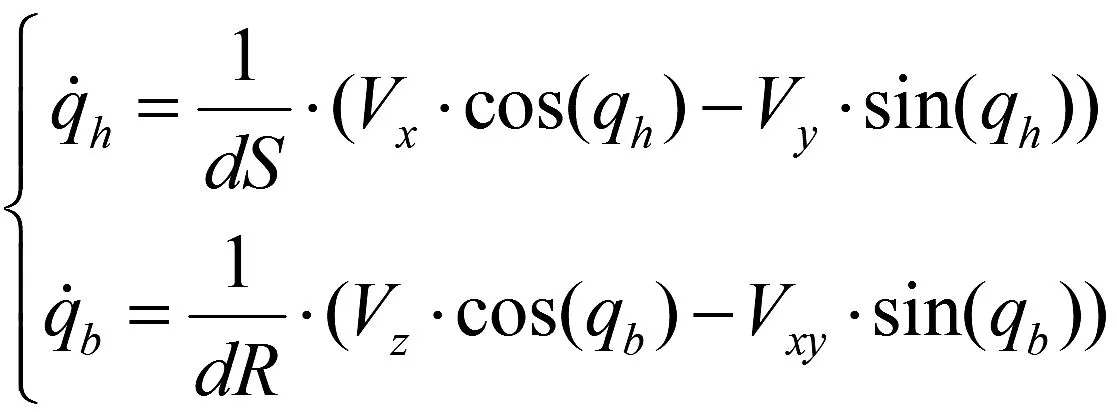
dS、dR分别为弹目水平距离、斜距：

qh、qb分别为弹目实时航向、俯仰视线角信号：

Vxy为飞行器速度在水平面内的分量：

4 仿真验证及结果分析

对导引头跟踪丢失后的控制效果进行数学仿真验证，在数学仿真过程中，假设飞行器发射高度为5000m，射程15Km，飞行器飞行速度300m/s，目标高度1000m。发射后导引头稳定跟踪目标，在距离目标5km处丢失目标。仿真中设惯导系统输出的航向/俯仰姿态角误差为0.25°（1σ），导引系统输出的航向/俯仰框架角误差也为0.25°（1σ），测高系统输出的高度包含常值误差和随机误差两部分，常值误差为飞行高度×5%，随机误差幅值为15m（1σ）。离散系统采样时间为0.02s。

在仿真过程中，首先生成飞行器飞行轨迹的理想坐标数据；在此基础上根据噪声误差模型对飞行高度、飞行器航向/俯仰姿态角、导引头框架角等加入了测量噪声；以高度、角度测量数据为观测量采用目标被动定位算法对目标进行定位；当导引头丢失目标后根据目标被动定位结果解算理论导引信号控制飞行器朝目标飞行。为了验证随机噪声条件下飞行控制效果，根据以上步骤进行了20次仿真，目标定位结果如图4所示。

图4 目标被动定位结果

从仿真结果看，目标被动定位结果收敛。由于初始状态估值误差及噪声的影响，在起始时刻目标定位结果误差较大，之后随着时间的增加滤波结果逐渐收敛，定位误差逐渐减小，在8s之后目标定位结果与实际距离趋于一致，目标定位误差在200m以内。

飞行器与目标点不同距离处导引头丢失目标情况下的命中结果见表1。

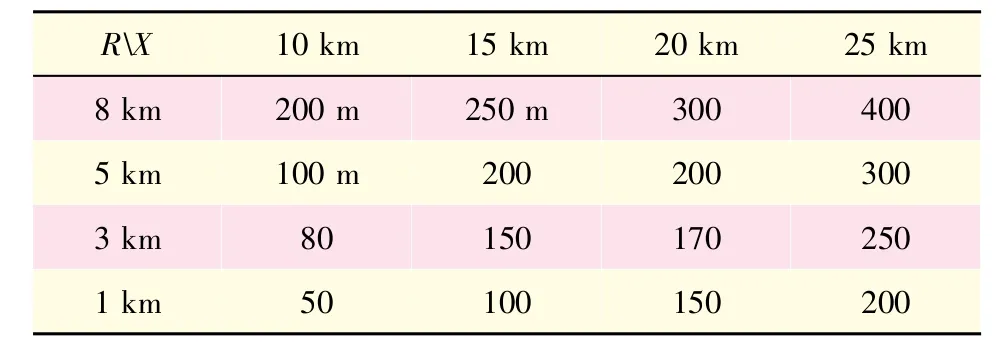
表1 导引头丢失目标情况下的命中效果

从仿真结果看，导引头跟踪丢失情况下的飞行控制稳定。导引头跟踪丢失情况下的命中结果与目标被动定位结果相关，目标定位精度越高，命中精度也越高。相同发射高度条件下，射程越近，目标被动定位精度越高，命中点偏差也越小；导引头跟踪丢失时刻距离目标越近，目标被动定位算法收敛时间越长，定位精度较高，最终的命中精度也越高。

5 结语

在导引头稳定跟踪过程中通过目标被动定位算法实时估算弹目飞行器与目标点相对位置信息，当导引头跟踪丢失后根据估算得到的相对位置信息和惯导输出的飞行器实时位置、速度信息解算理论导引信号，并根据该信号生成控制指令控制飞行器朝目标飞行。给出了目标被动定位算法和理论导引信号解算方法。对导引头跟踪丢失后的控制效果进行了数学仿真验证，并对目标被动定位结果和跟踪丢失情况下的命中精度进行了分析。

[1]包桂秋等.图像导航技术的发展和应用[J].航空计测技术，2003，23(6)：1-4.

[2]孙德波等.惯性/图像组合导航中的双模态双滤波器研究[J].宇航学报，2002，23(5)：5-9.

[3]唐涛等.改进的EKF算法在目标跟踪中的运用[J].光电工程，2005，32(9)：16-18.

[4]王敏.分析预测理论以及在空间位置探测数据处理中的应用 (II)空间位置方程与探测数据分析[J].舰船电子工程，2004(24),5:5-17.

[5]高磊.目标被动定位与跟踪技术[J].航天控制，2003，3：70-74.