边坡爆破对既有高边坡的振动影响分析
2018-05-08■王华
■王 华
(福建省交通规划设计院,福州 350004)
1 引言
随着公路工程不断建设发展,新建边坡临近既有边坡的情况越来越普遍,因此分析新建边坡建设的影响并提出合理的应对措施,是此类边坡工程建设过程中亟需解决的问题。已有文献更多地集中在研究边坡开挖后的长期稳定性问题[1,2]。但是,新建边坡爆破施工易造成既有边坡岩体原有的节理、裂隙进一步扩展,严重时还可能造成岩体沿已有结构面滑移,直接影响边坡的整体稳定性[3,4]。因此,分析爆破振动效应对边坡的影响显得尤为重要。国内有研究者利用有限元法对爆破荷载作用进行数值模拟分析,得到了较为准确的结果,这说明了利用数值模拟方法解决该类问题的可靠性[5,6]。
本文以福建省漳州市某公路工程新建边坡作为研究对象,对临近高速公路匝道高边坡段落范围内爆破施工过程进行三维动力数值模拟分析,确定了爆破荷载在不同位置对既有高边坡的振动影响,制定了安全合理的爆破方案,并对同类工程具有指导意义。
2 爆破振动效应判据标准
我国《爆破安全规程》(GB6722-2014)[9]中,提出了永久性匝道高边坡各频率范围内的安全允许爆破振速如表1所示。根据依托工程情况,采用浅孔爆破施工方案,因此取振动速度的控制值为10cm/s。
3 爆破振动影响数值模拟分析
3.1 工程概况
福建省漳州市某公路工程新建边坡工程与既有高速公路匝道边坡相邻,其交叉位置相互关系具体如图1所示。
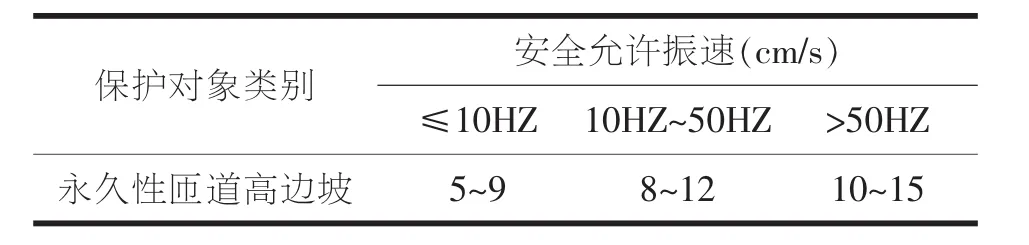
表1 爆破振动安全允许标准
新建公路边坡最大边坡高度为29.6m,共4阶,爆破开挖区域基岩主要以中风化花岗岩和散体状强风化花岗岩为主。既有匝道高边坡的最大边坡高度为35.1m,共4阶,以散体状强风化花岗岩~碎块状强风化花岗岩为主,采用M7.5浆砌片石拱型骨架防护,典型横断面如图2所示。
由于依托工程新建边坡与既有边坡的空间位置关系复杂,且爆破振动荷载作用过程对边坡动力响应有较大影响,因此本文采用基于时程分析的三维动力有限元法进行数值模拟。
3.2 爆破计算模型及参数
基于MIDASGTS NX有限元分析软件,建立三维有限元模型,并施加爆破时程荷载,分析既有匝道高边坡的振速和应力响应。通过调整爆破位置,从而确定满足安全爆破振动速度的爆破距离。

图1 交叉位置相互关系
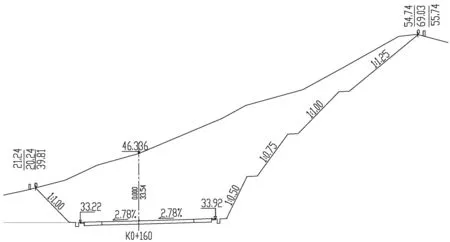
图2 既有匝道高边坡横断面图
计算模型纵向长313m,横向长598m,高度方向长60m,采用三维有限元模型,共划分23468个单元,31810个节点,岩土采用十结点四面体高阶实体单元模拟,如图3~4所示。

图3 边坡开挖前计算模型

图4 边坡开挖后计算模型
3.2.1 本构模型与边界条件
岩土具有复杂的变形特征,且随加载条件的变化而发生变化,本构模型虽然有很多种,但实际上并不存在一种本构模型能模拟实际土体的所有复杂变形特征。一个合理的本构模型应该满足参数易确定性,理论上的严格性和计算机实现的可能性。本文研究的边坡岩体主要由全风化花岗岩和散体状强风化花岗岩组成,可视为各向同性体,计算时采用Mohr-Coulomb强度准则。
由于岩体的动弹性模量Ed都普遍大于静弹性模量Eme,可利用岩体完整性系数Kv得到动弹性模量和静弹性模量的换算关系。按地质纵断图中的描述,取Kv为0.35~0.15,取j为0.2。因此,选定爆破动力分析计算参数如表2所示。
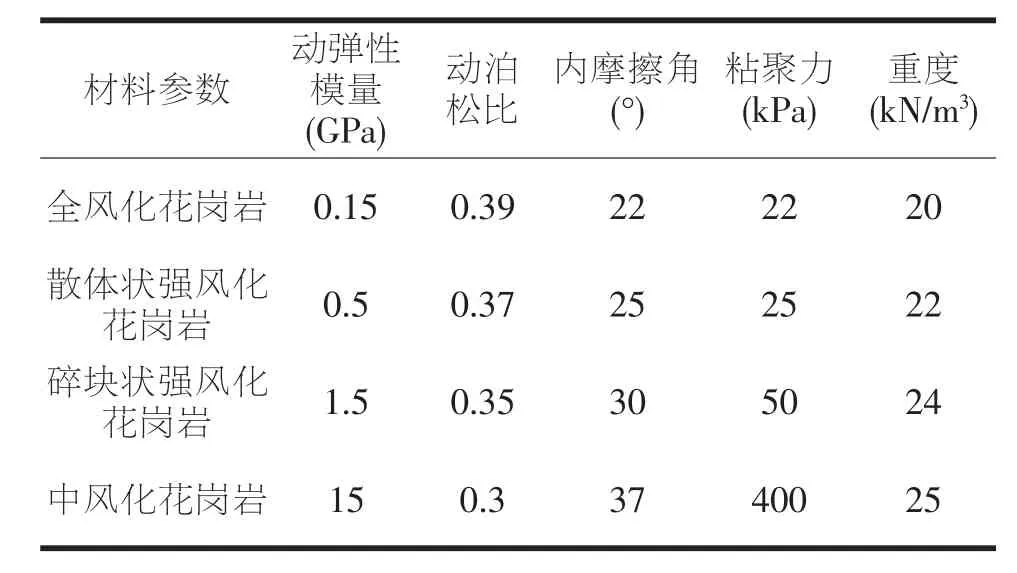
表2 爆破动力分析计算参数
对于动力分析,建立一般的边界条件会由于波的反射作用而产生很大的误差。计算时采用粘弹性边界既可以约束动力问题中的零频分量,能够模拟人工边界外半无限介质的弹性恢复性能,具有良好的稳定性和较高的精度。因此边界条件中除地表为自由边界外,其余边界面均施加了法向曲面弹簧。
3.2.2 爆破等效荷载
浅孔爆破施工方案根据开挖深度分一个或两个台阶进行爆破,边坡采用光面爆破。本次计算拟定炮孔直径45mm,深度H=4m,底板抵抗线Wp=1.45m,超钻深度h=0.2m,孔距 a=2m,排距 b=2m;炸药单耗 q=0.45kg/m3,炮孔方向:中间主炮孔取垂直孔,边坡光面孔与边坡坡率相同。考虑到爆破振速跟炸药量密切相关,为控制振速,单次爆破按纵向小台阶爆破,单次纵向爆破4m,共3个爆孔,单孔装药量5kg,共15kg。
爆破荷载采用美国National Highway Institute里提及的公式,每1kg炸药的爆破压力如下:

式中:Pdet为爆破压力,ρ为炸药比重 (取为1g/cm3),Ve为爆破速度(取为300000cm/s),PB为作用在孔壁面上最大爆破压力,dc为火药直径,dh为孔眼直径。
根据公式(2)求得每1kg炸药的最大爆破压力PB为20.9MPa。为控制振速,考虑施工时按纵向小台阶爆破,单次纵向爆破4m,共3个爆孔,单孔装药量5kg,共15kg。本次计算取单孔爆破压力为104.5MPa,考虑三个孔同时起爆。
由于爆破压力是随时间变化的,计算中采用以下动压力时程公式:
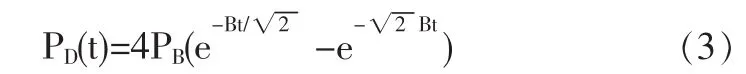
式中:B=16338,为荷载常量。
3.2.3 计算工况
为了分析在边坡不同位置起爆对既有高边坡的影响,本文设计了6种工况,各工况的起爆位置如图5所示。表3列出各工况爆破点距新建边坡与既有边坡交点的距离。
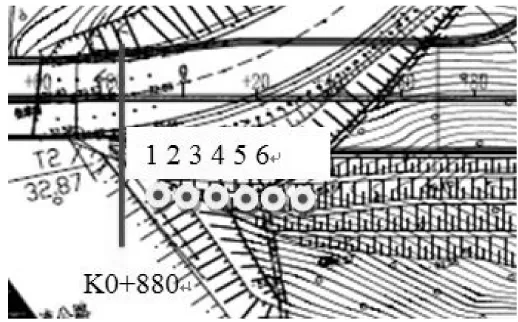
图5 爆破荷载施加位置

表3 爆破荷载施加位置
3.3 数值模拟结果与分析
3.3.1 爆破振动速度结果
计算得到的工况1(爆破点距离既有匝道高边坡最近)既有边坡的最大爆破振动合速度为155.7cm/s,位于爆破点附近新建边坡和既有匝道高边坡的交点处,发生于0.043s时刻。
绘制出不同工况下既有匝道高边坡最大振动速度随距离变化曲线分别如图6、表4所示。经内插可知起爆点距新建边坡与既有边坡交点23m以外时,既有边坡的最大振动速度小于10cm/s,满足《爆破安全规程》允许振动速度要求。
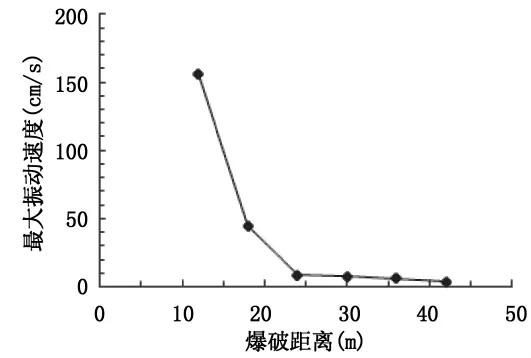
图6 各工况既有匝道高边坡最大振动速度变化曲线
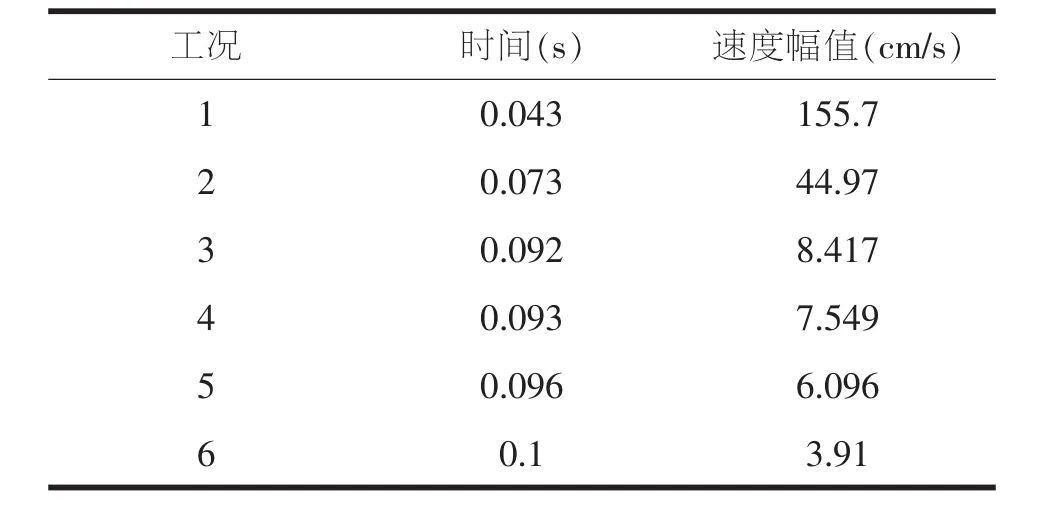
表4 各工况既有匝道高边坡最大振动速度统计表
3.3.2 应力结果
图7~8为计算工况1爆破后,既有匝道高边坡表面监测点的第一主应力(最大拉应力)和最大剪应力结果。当爆破时刻为0.043s时,边坡表面最大拉应力达到最大值,为0.64MPa,最大剪应力为 0.32MPa,已接近或超过M7.5砂浆的抗拉和抗剪强度0.54MPa,说明在工况1爆破作业下,存在浆砌片石开裂脱落、掉块的危险。
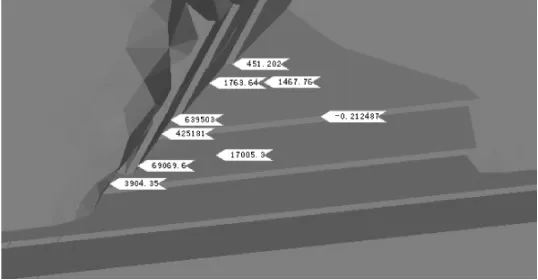
图7 既有匝道高边坡第一主应力横断面图
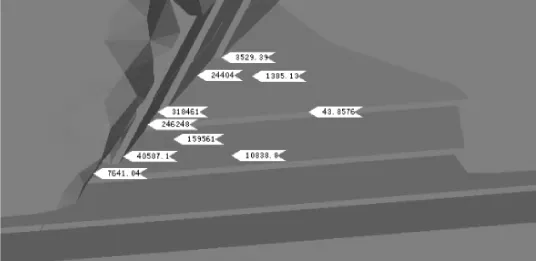
图8 既有匝道高边坡最大剪应力横断面图
计算得到各爆破工况,既有匝道高边坡的最大主应力、最大剪应力结果。绘制出既有匝道高边坡第一主应力及最大剪应力随距离变化曲线分别如图9、10所示。从图中可以看出,最大拉应力和剪应力随距离衰减较快,起爆点距既有匝道边坡(桩号K0+880)18m以外时,既有匝道边坡的浆砌片石砌体破坏风险较小。
4 结论
基于福建省漳州市某公路工程,建立了爆炸荷载作用下临近匝道高边坡的动力响应模型,采取露天爆破开挖,分析不同的爆破位置下边坡的速度场和应力场的分布规律。得到如下结论:
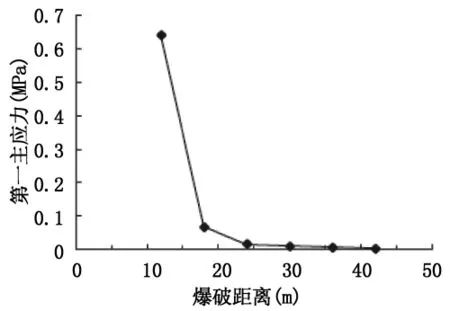
图9 既有匝道高边坡第一主应力随距离变化曲
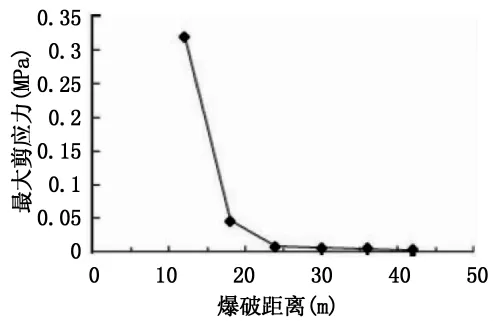
图10 既有匝道高边坡最大剪应力随距离变化曲线
(1)爆源附近区域最大振动速度衰减速率大于较远区域,显指数衰减规律。
(2)新建边坡进行爆破施工对既有匝道高边坡存在岩体开裂、浆砌片石脱落的风险。当起爆点距既有匝道边坡(桩号K0+880)23m以外时,最大振动速度满足要求,匝道边坡的浆砌片石砌体破坏风险也较小。对于类似情况的近接工程,可参考本文的方案进行振动影响分析。
[1]高文学,刘宏宇,刘洪洋,等.爆破开挖对路堑高边坡稳定性影响分析[J].岩石力学与工程学报,2010,29(增 1):2982-2987.
[2]张华其,张松新,周华杰,等.爆破振动对周边建筑物的影响[J].爆破,2007.24(2):98-101.
[3]宗琦,汪海波,周胜兵.爆破地震效应的监测和控制技术研究[J].岩石力学与工程学报,2008,27(5) :938-945.
[4]李宁,姚显春,张承客.岩质边坡动力稳定性分析的几个要点[J].岩石力学与工程学报,2012,31( 5) :873-881.
[5]夏祥,李俊如,李海波,等.爆破荷载作用下岩体振动特征的数值模拟[J].岩土力学,2005,26(1):50-56.
[6]林士炎,李长洪,乔兰,等.爆破震动对高速路边坡影响的数值模拟[J].北京科技大学学报,2003,25(6):507-509.
[7]国家安全生产监督管理总局.GB 6722-2014,爆破安全规程[S].北京:中国标准出版社,2014.
