基于混合模型的油松林分蓄积量预测模型的建立

王少杰，邓华锋，向 玮，黄国胜，王雪军

(1 北京林业大学 林学院，北京 100083；2国家林业局调查规划设计院，北京 100714)

在森林经营中，林分的生产潜力及效益的评价离不开蓄积量的大小估算，林分蓄积量是评价森林数量的主要指标，其大小可以反映经营单位经营森林的状况和水平[1-2]。常见的林分蓄积量模型可分为传统线性和非线性两类[3]，线性模型一般是以常见的林分变量，如林分年龄、林分平均密度、立地质量等为自变量构建的[4-5]；非线性模型主要是选用适应性较强的生长模型为基础模型，并在模型中引入林分变量将模型再次参数化来构建的[6-7]。但建立模型所采用的样地数据多为重复观测的固定样地，数据间存在异方差和时间序列自相关性，因此难以满足传统的回归模型独立等方差的前提要求[8]，且回归模型只能反映林分的总体平均生长状况，无法反映样地水平间的变化规律。而混合模型一方面通过引入随机参数，可以同时体现总体平均效应和个体间的差异，使得模型刻画更为精细；另一方面通过规定不同的方差协方差结构来描述数据间的异方差和自相关性，从而达到提高模型预估精度的目的[9-10]。

近年来，国内外已有一些学者利用混合模型在林业方面进行了研究，如预估林木树高[11-12]、胸径[13]、林分断面积[14-15]和枝条大小[16-17]等，均证明混合效应模型预估精度较仅含固定效应的传统回归模型高。对于林分蓄积量混合模型的研究，国内外基本上多集中在单水平混合模型上，如Fang等[18]利用非线性混合模型方法，通过考虑样地随机效应及自相关性，建立了不同经营措施效应下的美国沼泽松林分蓄积量模型，结果显示，混合模型的预测精度与传统方法相比有很大的提高；Zhao等[19]利用非线性混合模型，对4种不同经营措施处理下火炬松林分蓄积量的生长进行了拟合，得出混合模型能较好地解决重复观测数据不等的问题；李春明[20]基于非线性混合效应的方法，建立了杉木人工林蓄积量联立方程组模型，较好地解决了内生变量间误差传递的问题。而对于嵌套两水平油松林分蓄积量混合模型的研究少见报道。

油松(PinustabulaeformisCarr.)为阳性树种，喜生长在排水良好的酸性土壤中，是北京市主要的造林绿化树种之一，面积7.9万hm2，占北京市森林总面积的25%，在保护生态环境安全方面发挥着至关重要的作用[21]，而目前涉及油松蓄积量混合模型的研究还较少，因此准确预估油松林分蓄积量，提高油松经营管理水平非常必要。本研究基于北京地区油松连续清查数据，将样地按初期的林分密度分为5个水平区间，在建立的油松林分蓄积量基础模型上，又考虑了油松的林分初始株数密度水平效应(后面简称密度水平效应)、油松林分样地效应及嵌套两水平效应，分别构建油松混合效应模型，以期为准确地预估油松林分蓄积量提供方法支撑，从而更好地经营北京地区的油松林分。

1 研究区概况

北京市地处华北平原北端，与天津市、河北省毗邻。北京市气候属于暖温带半湿润大陆性季风型气候，四季分明，气候干燥。降雨分布不均匀，夏季炎热多雨，冬季寒冷干燥。年平均气温9～12 ℃，年平均降水量500～700 mm，受季节性影响，降水主要集中在7-8月，约占总降水量的75%。北京中山区中、下部有大面积的萌生丛和灌丛，局地生长有蒙古栎、辽东栎、油松等次生林；低山区分布有不同种类灌丛，主要为荆条、酸枣；盆地和沟谷地带主要有杨、柳、榆、柿子等。北京市下辖有16个区，在怀柔、密云、平谷、海淀、延庆和平谷等区县都有油松分布。

2 材料与方法

2.1 数据来源

试验采用北京市2001、2006、2011年三期一类连续清查的油松人工林固定样地数据，样地面积为0.066 7 hm2。剔除数据缺失、异常和记录不详的样地，从三期样地中选出每期均有的76块油松样地，共计228块。将76块样地按照初期的林分株数密度(ID)分成Ⅰ(ID<400株/hm2)、Ⅱ(400≤ID<800株/hm2)、Ⅲ(800≤ID<1 200株/hm2)、Ⅳ(1 200≤ID<1600株/hm2)、Ⅴ(ID≥1 600株/hm2)5个水平。从3期76块复测样地中选取相同的56块样地(即168块)数据作为建模数据，剩下20块样地(即60块)数据作为检验数据。数据来源样地详细情况见表1。

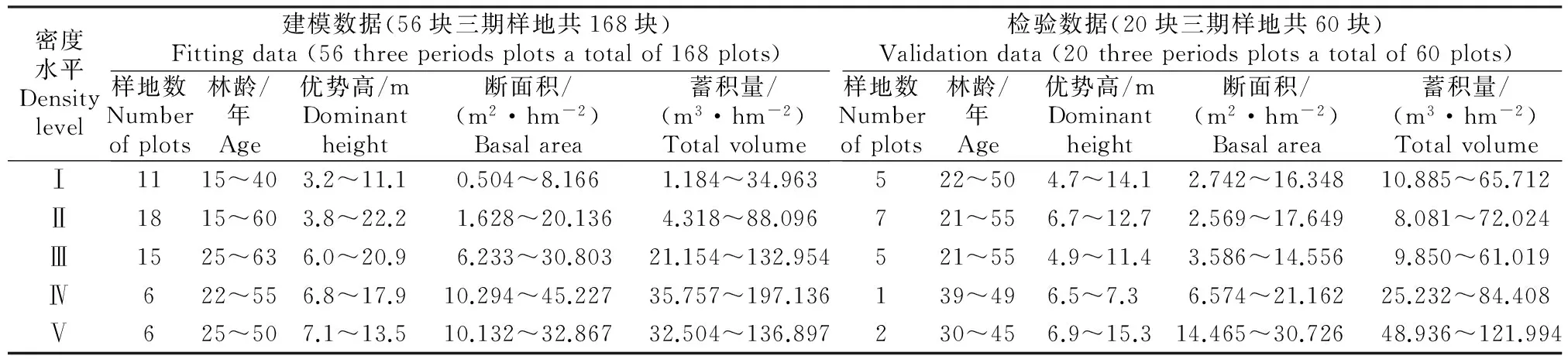
表1 北京油松林分蓄积量预测模型建立数据来源样地的基本情况Table 1 Basic situation of sample plots for constructing Pinus tabulaeformis stand volume model in Beijing

2.2 基础模型

除人为经营影响外，林分蓄积量主要受立地和林分密度的影响。立地为人为不易改变的因子，林分密度可通过经营控制达到预期目标。衡量林分密度的指标有很多，如株数密度、断面积、郁闭度、林分密度指数等，其中断面积易于测定，不仅与林木株数及大小相关，还与林分蓄积量紧密相关。根据这些条件，仿照单株立木材积方程式，选用断面积(G)和优势木高(HT)建立林分蓄积量(V)一般表达式：V=aG×HT。若直接采用上式建模,则模型的误差为乘积误差，为降低模型误差，将表达式两边取对数进行线性变换[22]，为避免模型表达式左边小于0导致拟合的不稳定，参考李春明[20]的方法，用ln (V+1)替换lnV，得到林分蓄积量模型表达式如下：

ln (V+1)=a1+a2lnHT+a3lnG+εv。

(1)

式中：V为样地的林分蓄积量，HT为样地的优势木平均高，G为样地的林分断面积，εv为蓄积量估测误差，a1、a2和a3为待估参数。

2.3 线性混合模型

线性混合模型是通过在线性模型中引入随机效应建立的。线性混合模型包括单水平和多水平线性混合模型，以单水平线性混合模型为例，其形式如下[23]：

(2)

式中：yij是第i块样地第j次蓄积量观测值，m为样地数量，ni为第i块样地连续观测的次数，Xij为(ni×p)维设计矩阵，β为(p×1)维固定参数向量，Zij为(ni×q)维设计矩阵，bij为与样地和区组水平相关的(q×1)维随机参数向量，εij为残差向量，Rij为(ni×ni)维协方差矩阵，D为区组水平间或样地间随机效应向量。

通过(2)式构建单水平线性混合模型，来分析林分初期密度或样地对林分蓄积量的影响。(2)式的单水平线性混合模型可被扩展到嵌套两水平线性混合模型，形式类似于(2)式[13]。此时由于每个林分密度水平中嵌套一定数量的样地，因此将林分密度水平和样地分别作为第1水平随机效应因子、第2水平随机效应，通过构建嵌套两水平线性混合模型，以分析林分密度和样地对林分蓄积量的影响。确定混合模型之前，需要明确以下3个结构[15]。

1)混合模型参数的确定。对基础模型衍生出的混合模型采用极大似然参数估计方法，比较各模型的AIC、BIC和Log-likelihood值，AIC和BIC值越小、Log-likelihood值越大的模型被确定为最优模型。

2)方差协方差结构。数据间的异方差和自相关性问题需要在模型中考虑。林业中，常用下式描述模型的异质性和自相关性[24]：

(3)

式中：σ2为残差的方差值；Gij为描述水平或样地内异方差的矩阵，矩阵形式为对角矩阵；Γij为描述时间相关性的结构函数。

本研究采用3种自相关结构描述林分蓄积量的时间相关性，分别为一阶自回归矩阵[AR(1)]、一阶自回归与滑动平均模型相结合的矩阵模型[ARMA(1,1)]及复合对称矩阵模型CS；采用常见的3种异方差结构，即幂函数(Power)、指数函数(Exp)和常数加幂函数(ConstPower)来消除异方差。异方差结构的表达式如下：

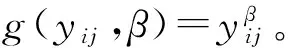
(4)

指数函数：g(yij,β)=exp(βyij)。

(5)

(6)

式中：yij为固定效应参数预测值，δ、β为待定参数。

3)确定随机参数协方差结构。随机参数协方差结构描述水平(样地)间的可变性，研究采用R语言nlme功能中默认的方差结构为随机参数协方差结构，即广义正定矩阵结构。以包括2个随机参数(u、v)的协方差矩阵结构为例，u、v分别为模型参数a1和a3的随机效应参数值，形式如下：

(7)

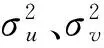
2.4 模型评价与检验指标

(8)

(9)

(10)

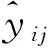
为了避免模型参数过多，评估2个模型中哪个更适合当前数据，利用似然比检验：

LRT=2lg (L1/L2)=2lg (L1-L2)。

(11)

式中：L1、L2分别为模型1和2的最大似然函数。

LRT服从自由度为k1-k2的卡方分布，k1、k2为2个模型的自由度；给定可靠性α=0.05，当LRT大于等于给定α所对应的卡方值，说明2个模型差异显著；反之，说明2个模型不显著，选择随机效应参数少的模型。

3 结果与分析

3.1 油松林分蓄积量基础模型的拟合结果

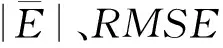
表2 油松林分蓄积量基础模型的拟合结果Table 2 Simulation of Pinus tabulaeformis stand volume basic model

3.2 油松林分蓄积量的单水平线性混合模型

3.2.1 随机效应参数的确定 (1)基于密度水平效应。以5个密度水平作为随机效应，考虑不同随机效应参数组合，对模型进行拟合，拟合结果见表3。表3显示，通过比较AIC、BIC和Log-likelihood值的大小，可知具有随机参数的模型3个指标均优于传统的基础模型；当模型中有1个随机参数时，a3为随机参数时模型拟合精度最高；当模型中有2个随机参数时，a1和a3为随机参数时模型的拟合精度最高；与a1和a3同时作为随机参数的模型相比，a1、a2、a3同时作为随机参数的模型拟合效果无显著提高(P=0.508 1)。因此，将a1和a3同时作为随机参数的模型选为最优基础混合模型。

(2)基于样地效应。与3.2.1的研究方法相同，考虑样地效应，对模型进行拟合，共有7种模型收敛情况，拟合结果见表3。根据3个评价指标及似然比检验结果可知，将a1和a3同时作为随机参数时的模型为最优基础混合模型(表3)，这与基于密度水平效应确定的随机效应参数结果相同。

3.2.2 单水平误差的异方差和时间自相关性 (1)基于密度水平效应。连续观测的数据之间存在异方差，采用3种异方差结构来消除样地间的异方差性，结果见表4。

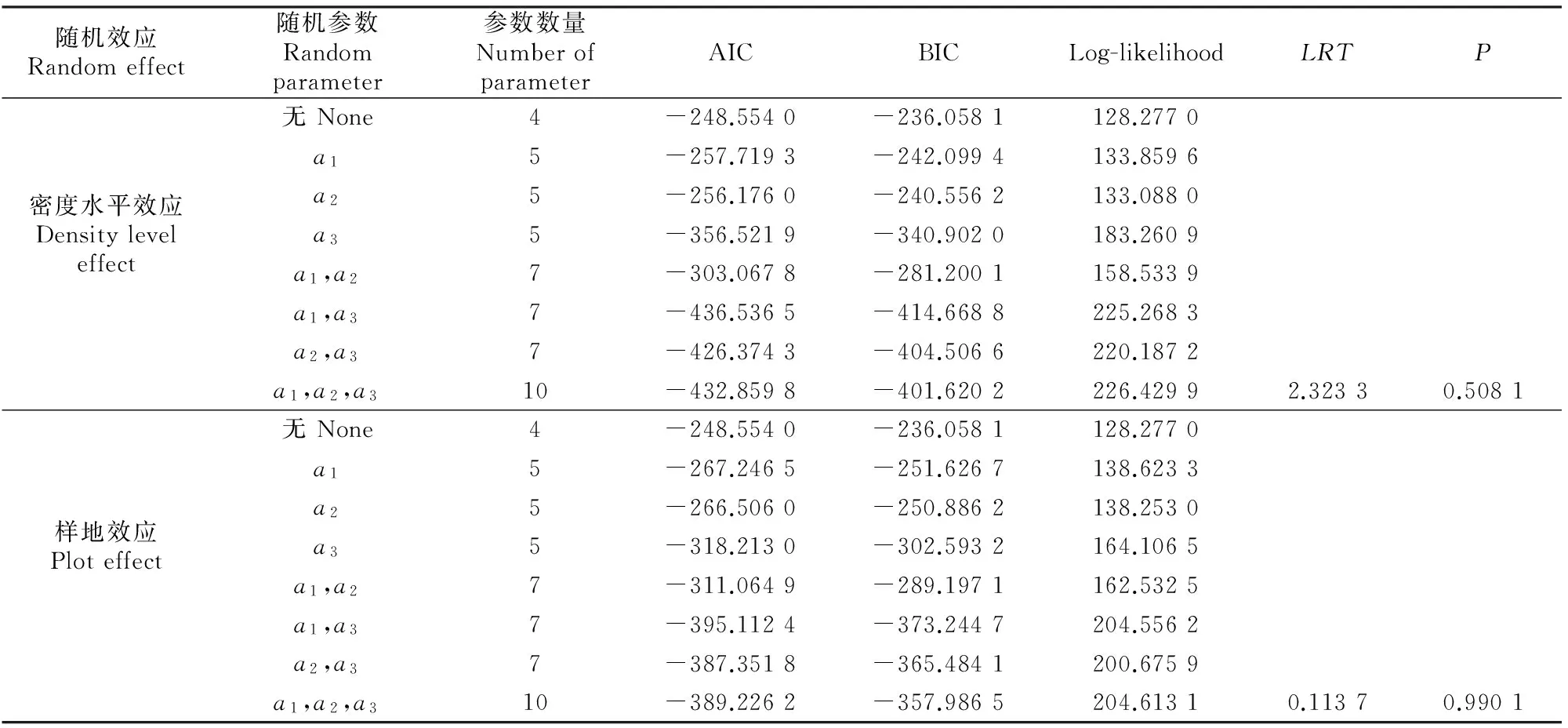
表3 选用不同随机参数时油松林分蓄积量单水平混合模型拟合结果的比较Table 3 Comparisons of single-level mixed models for Pinus tabulaeformis stand volume based on different random parameters

表4 基于不同异方差结构的油松林分蓄积量单水平混合模型模拟结果的比较Table 4 Comparisons of single-level mixed models for Pinus tabulaeformis stand volume based on different heteroscedasticity structures

根据LRT值和P值可知，考虑3种异方差结构的模型和未考虑异方差结构的模型之间差异显著，说明3种异方差结构均可以消除数据间的异方差。比较AIC、BIC和Log-likelihood值，指数函数的AIC和BIC值最小，Log-likelihood值最大，故密度水平效应混合模型选择指数函数描述异方差结构(表4)。图1为消除异方差前后的残差图。其中考虑异方差的残差图(图1-B)大致呈均匀分布，明显优于未考虑异方差结构时的结果(图1-A)，表明指数函数异方差结构较好地消除了数据间的异方差性。

连续观测的数据之间不仅存在异方差，还存在时间序列自相关性。研究采用3种自相关结构描述样地内时间序列相关性(即AR(1)、[ARMA(1,1)]、CS)，拟合结果见表5。根据LRT值和P值可知，混合模型中加入时间序列自相关性后，均能显著提高蓄积量模型的拟合效果，且尤以[ARMA(1,1)]结构拟合结果最好(表5)，因此选用[ARMA(1,1)]来描述油松样地的自相关性结构。

(2)基于样地效应。与密度水平效应相同，用3种异方差结构消除样地间的异方差性，拟合结果见表4。由表4可知，只有指数函数异方差结构收敛，其他2种结构拟合结果均不收敛，说明样地效应混合模型选择指数函数可以消除数据间的异方差性。由图2-A可见，未考虑异方差的残差图随着预测值的增大呈现扩张趋势，显示出了一定的异方差性，且残差图散点分布较散；考虑异方差结构的残差图分布较集中，基本消除了数据间的异方差性(图2-B)。

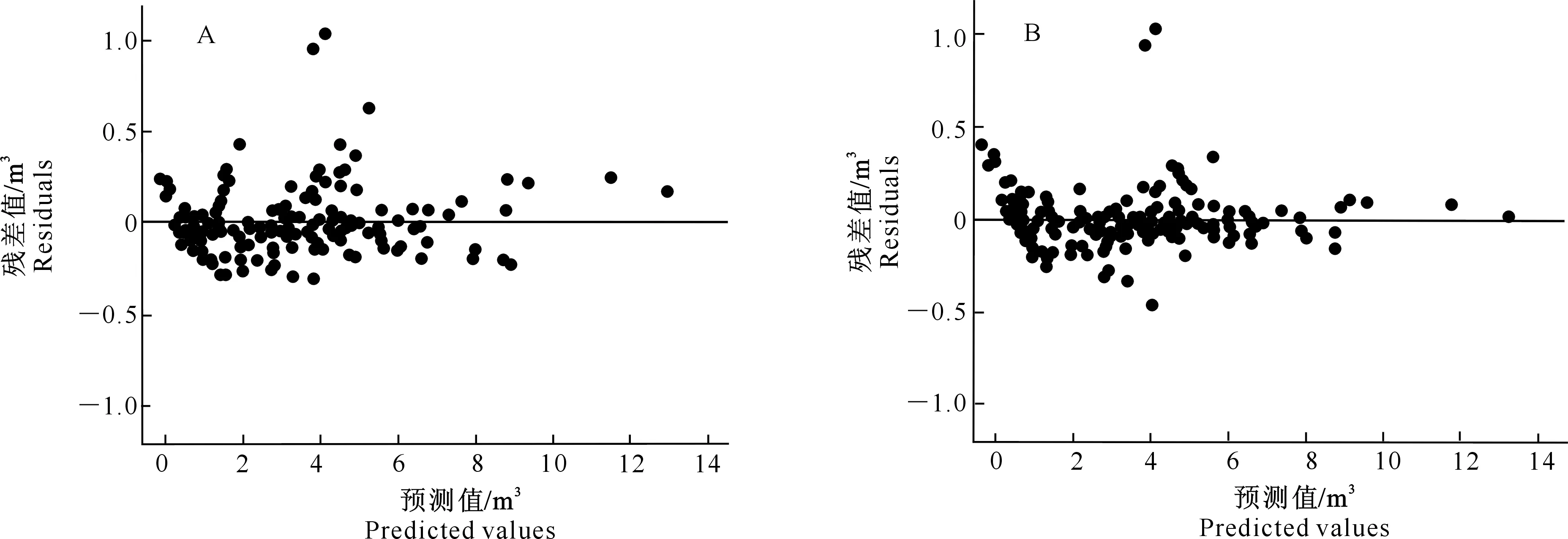
图1 未考虑异方差结构(A)和考虑异方差结构(B)的密度水平效应混合模型的油松林分蓄积量预测值残差分布Fig.1 Residual plots of stand volume predicted values without considering heteroscedasticity structures (A) and considering heteroscedasticity structures (B) based on mixed model of Pinus tabulaeformis stand density level effect

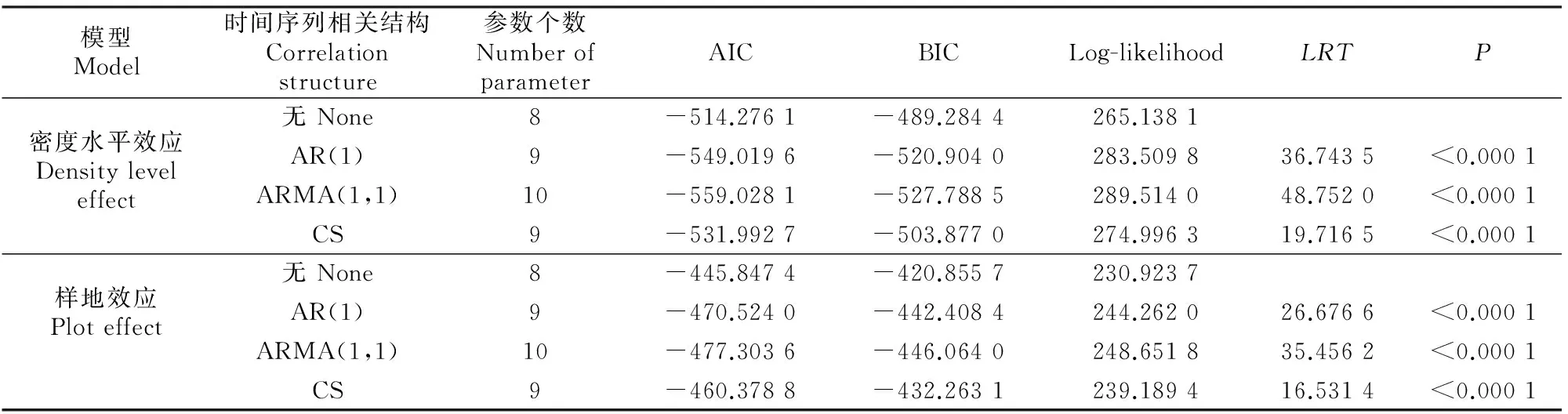
模型Model时间序列相关结构Correlationstructure参数个数NumberofparameterAICBICLog-likelihoodLRTP无None8-514.2761-489.2844265.1381密度水平效应DensityleveleffectAR(1)9-549.0196-520.9040283.509836.7435<0.0001ARMA(1,1)10-559.0281-527.7885289.514048.7520<0.0001CS9-531.9927-503.8770274.996319.7165<0.0001无None8-445.8474-420.8557230.9237样地效应PloteffectAR(1)9-470.5240-442.4084244.262026.6766<0.0001ARMA(1,1)10-477.3036-446.0640248.651835.4562<0.0001CS9-460.3788-432.2631239.189416.5314<0.0001

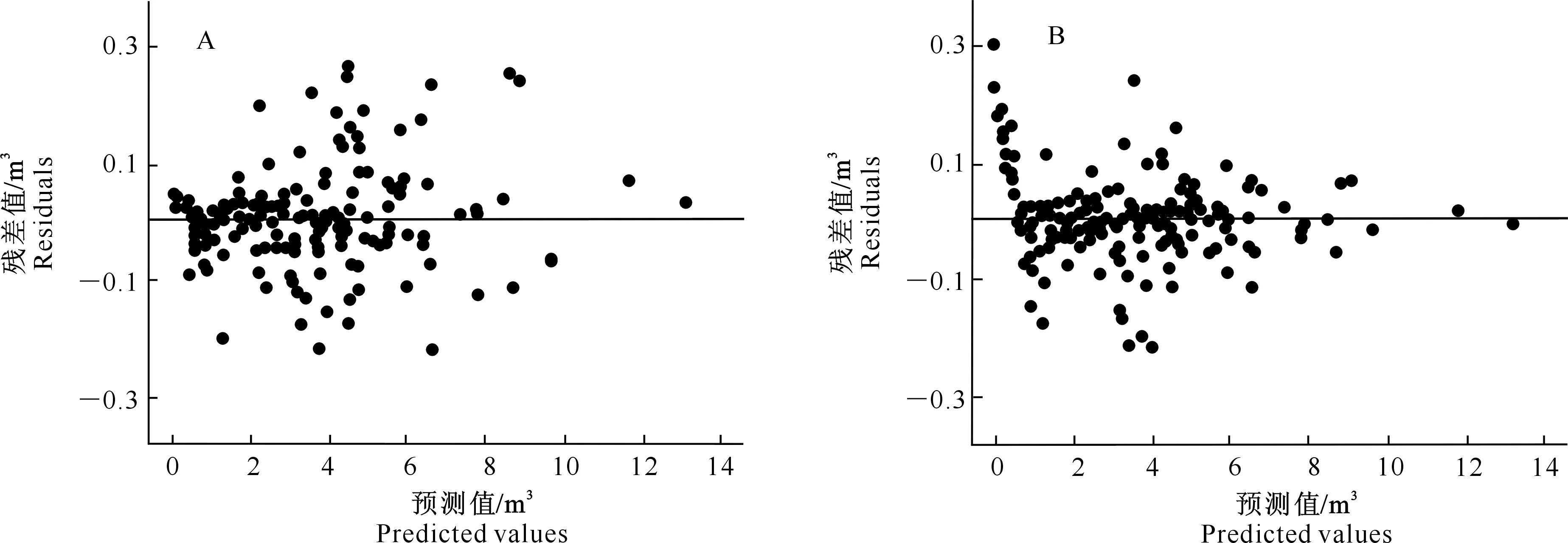
图2 未考虑异方差结构(A)和考虑异方差结构(B)的样地效应混合模型油松林分蓄积量预测值残差分布Fig.2 Residual plots of stand volume predicted values without considering heteroscedasticity structures (A) and considering heteroscedasticity structures (B) based on mixed model of Pinus tabulaeformis plot effect

同样在样地效应模型中考虑时间序列自相关性，由表5的拟合结果可知，时间序列结构加入到模型后，均能够显著提高模型的拟合精度；[ARMA(1,1)]结构的AIC、BIC值分别为-477.303 6和-446.064 0，在3种时间序列结构中最小；Log-likelihood值为248.651 8，在3种时间序列结构中最大，故选择[ARMA(1,1)]结构加入到混合模型中。

3.3 油松林分蓄积量的嵌套两水平线性混合模型

3.3.1 与单水平混合模型拟合结果的比较 根据上述3.2.1的拟合结果，模型中加入2种效应，参数a1和a3为同时含有密度水平效应和样地效应的随机效应参数。对嵌套两水平与2种单水平效应混合模型的拟合结果进行方差分析，结果见表6。由表6可知，嵌套两水平混合模型的3个评价指标最优，且由似然比检验知，嵌套两水平混合模型与单水平混合模型差异极显著(P<0.000 1)。

表6 油松林分蓄积量嵌套两水平混合模型与单水平混合模型拟合结果的比较Table 6 Comparisons of two-level and single-level stand volume mixed model for Pinus tabulaeformis

3.3.2 嵌套两水平误差的异方差和时间自相关性 与单水平混合模型研究方法相同，用3种异方差结构和3种时间序列自相关结构描述样地间的异方差性及自相关性。由于考虑时间序列自相关性后差异不显著，故嵌套两水平混合模型不考虑时间自相关性结构。3种异方差结构中，幂函数结构不收敛，经过方差分析，另外两种结构与未考虑异方差结构有显著差异，其中指数函数结构优于常数加幂函数结构，用其可以更好地消除数据间的异方差性(表7)。

表7 基于不同异方差结构的油松林分蓄积量嵌套两水平混合模型模拟结果的比较Table 7 Comparisons of two-level mixed model for Pinu stabulaeformis stand volume based on different heteroscedasticity structures

3.4 油松林分蓄积量不同模型的参数估计

综合上述分析结果，表8和表9给出了基础模型、单水平(密度水平效应或样地效应)混合模型、嵌套两水平混合模型的各参数估计值及统计量指标。

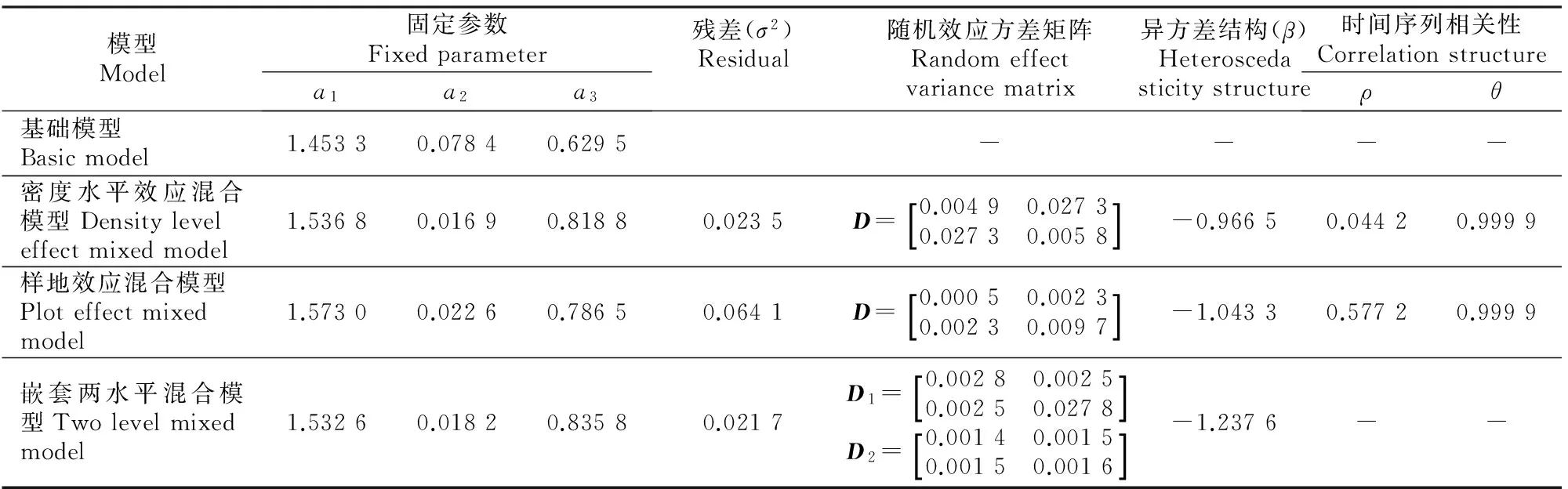
表8 油松林分蓄积量不同模型参数的拟合结果Fig.8 Parameter estimatesfor different models of Pinus tabulaeformis stand volume

表9 油松林分蓄积量不同模型的拟合统计量Fig.9 Fitting statistics for different models of Pinus tabulaeformis stand volume

表10列出了嵌套两水平模型中各密度水平区间的随机效应值。由表10可知，水平Ⅰ对应的随机效应均为负值，且随机效应值v的绝对值最大；水平Ⅲ和水平Ⅳ对应的随机效应均为正值，剩余2个水平的随机效应值均为一正一负。

表11列出了10组样地的样地随机效应值，由于样地数据较多，故本文没有全部给出。由表10和表11可知，嵌套两水平混合模型中样地对应的随机效应绝对值整体小于密度水平对应的随机效应绝对值，且均非常接近0，因此嵌套两水平混合模型中，由样地带来的随机效应影响很小。

表10 油松林分蓄积量嵌套两水平混合模型的密度水平随机效应参数值Table 10 Density level random effects values of two-level mixed model for Pinus tabulaeformis stand volume

表11 油松林分蓄积量嵌套两水平混合模型的样地随机效应参数值Table 11 Plot random effects values of nested two-level mixed model for Pinus tabulaeformis stand volume

3.5 油松林分蓄积量不同模型的检验

采用未参与建模的20块样地的独立样本数据对基础模型、2个单水平混合模型和嵌套两水平混合模型的拟合结果进行检验，基础模型的检验是将变量带入模型中，用固定效应参数求出预估值，并与实际测量值分析比较；混合模型的检验则需利用公式(12)求出每个样地随机效应参数bk的值：

(12)

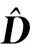
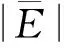
表12 油松林分蓄积量基础模型和考虑异方差结构及时间序列自相关性混合模型的检验结果Table 12 Validation for Pinus tabulaeformis stand volume basic model and mixed model considering heteroscedasticity structures and time series error autocorrelation

由图3可见，混合模型预测值残差分布均优于基础模型，且嵌套两水平混合模型残差图散点分布相对于2种单水平混合模型更加集中。图3进一步证明了表12的拟合结果。

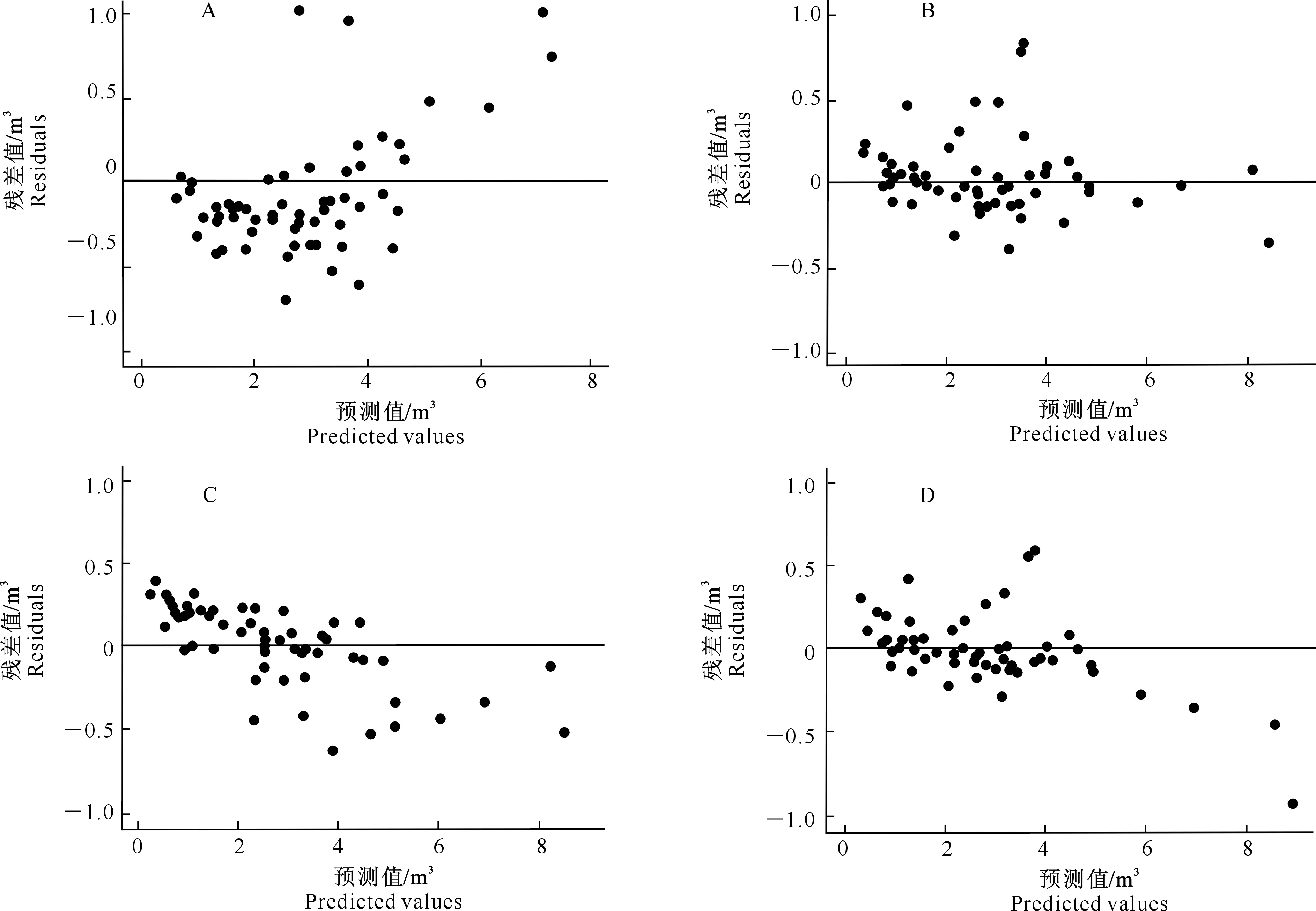
A.基础模型；B.密度水平效应混合模型；C.样地效应混合模型；D.嵌套两水平混合模型 A.Basic model;B.Density level effect mixed model;C.Plot effect mixed model;D.Two level mixed model

4 结论与讨论

本研究利用线性混合模型建立油松蓄积量生长模型，在考虑密度水平效应或样地效应时，a1和a3组合作为随机效应参数时模型拟合效果最好。其中，考虑密度水平效应的混合模型不仅可以描述不同初期株数密度对林分蓄积量生长的影响，而且能针对不同的初期密度林分进行量化分析比较；考虑样地效应的混合模型则可以更加准确地描述不同样地的林分蓄积量生长情况，但密度水平效应混合模型的拟合精度略优于样地效应混合模型；嵌套两水平混合模型的拟合精度高于单水平混合模型，这与符利勇等[13,25]、肖锐等[26]的研究结果一致，且嵌套两水平混合模型还可以分析各密度水平及样地对油松蓄积量的影响程度。在嵌套两水平混合模型中，水平Ⅰ对应的随机效应均为负值，其中v绝对值最大，则该林分初期密度对该水平油松蓄积量负贡献最大，水平Ⅲ和水平Ⅳ对应的随机效应均为正值，则其对蓄积量均为正贡献；样地效应的随机效应值都非常接近0，且样地间相差不大，表明样地间的立地质量、坡向、坡度等无显著差异。

本研究使用的数据为多次测量数据，因此建立的模型中既考虑了随机效应的异方差，又考虑了自相关性。单水平混合模型中，将3种异方差和3种时间自相关性结果引入模型中，利用AIC、BIC及Log-likelihood值评价不同模型的效果，可知无论是考虑密度水平效应还是考虑样地效应，指数函数(Exp)异方差结构和[ARMA(1,1)]相关性结构均显著提高了林分蓄积量的拟合效果，能够较好地描述模型的异方差性和自相关性问题；嵌套两水平混合模型由于考虑自相关性后不显著，仅在模型中考虑了异方差性，但拟合效果优于单水平混合模型。

本研究建立嵌套两水平混合效应模型时，随机效应参数是基于密度水平和样地两种单水平混合效应的研究结果确定的，并未对基础模型衍生出来的其他随机效应组合模型进行分析比较，其随机效应参数的确定是否可以直接基于单水平混合模型的结果，有待进一步研究。另外受数据量的限制，按林分株数密度划分的5个水平区间的样地分布不均匀，第Ⅳ、Ⅴ水平区间样地数较少，可能会对随机效应参数的估计有一定影响，需增加样本数量进一步分析比较。

[参考文献]

[1] 孟宪宇.测树学 [M].北京: 中国林业出版社，2006.

Meng X Y.Dendrometry [M].Beijing:China Forestry Publishing House,2006.

[2] 公宁宁,马履一,贾黎明,等.不同密度和立地条件对北京山区油松人工林树冠的影响 [J].东北林业大学学报,2010,38(5):9-12.

报道中模糊限制语与数字结合，告诉读者在新闻发生时的准确信息，让报道更具有严谨性和客观性，更加精确的传递了相关信息。

Gong N N,Ma L Y,Jia L M,et al.Effects of different stand densities and site conditions on crown ofPinustabulaeformisis plantations in Beijing mountain area [J].Journal of Northeast Forestry University,2010,38(5):9-12.

[3] 李春明.抚育间伐对人工林分生长的影响研究 [D].北京:中国林业科学研究院,2003.

Li C M.Effects of thinning on the growth ofLarixolgensisplantation [D].Beijing:Chinese Academy of Forestry,2003.

[4] 付小勇.云南松林分生长模型研究 [D].昆明:西南林业大学,2006.

Fu X Y.Study on stand growth models forPinusyunnanensis[D].Kunming:Southwest Forestry University,2006.

[5] Fang Z,Bailey R L,Shiver B D.A multivariate simultaneous prediction system for stand growth and yield with fixed and random effects [J].Forest Science,2001,47(4):550-562.

[6] 郎 荣,许建初,Timm Tennigkeit,等.基于样方数据的云南松林分生长模型研究:以云南省保山市杨柳白族彝族乡为例 [J].植物分类与资源学报,2011,33(3):357-363.

Lang R,Xu J C,Tennigkeit T,et al.A study of stand growth model forPinusyunnanensis(Pinaceae) based on plots data:a case study in Yangliu Township,Baoshan,Yunnan Province [J].Plant Diversity and Resources,2011,33(3):357-363.

[7] 高东启,邓华锋,王海宾,等.基于哑变量的蒙古栎林分生长模型 [J].东北林业大学学报,2014，42(1):61-64.

Gao D Q,Deng H F,Wang H B,et al.Dummy variables models inQuercusmongolicagrowth [J].Journal of Northeast Forestry University,2014，42(1):61-64.

[8] 李晓景.闽北天然阔叶林材种结构分析与生长收获预估模型 [D].福州:福建农林大学,2013.

Li X J.Analysis on timber assortment and growth-yield model of prediction for Natural broad-leaved forests in North Fujian [D].Fuzhou:Fujian Agriculture and Forestry University,2013.

[9] 李春明.混合效应模型在森林生长模型中的应用 [J].林业科学,2009,45(4):131-138.

Li C M.Application of mixed effects models in forest growth model [J].Scientia Silvae Sinicae,2009,45(4):131-138.

[10] 唐守正.生物数学模型的统计学基础 [M].北京: 科学出版社,2002.

Tang S Z.Statistical basis of biological mathematical model [M].Beijing:Science Press,2002.

[11] Calegario N,Daniels R F,Maestri R,et al.Modeling dominant height growth based on nonlinear mixed-effects model:a clonalEucalyptusplantation case study [J].Forest Ecology and Management,2005,204(1):11-21.

[12] 王冬至,张冬燕,张志东,等.基于非线性混合模型的针阔混交林树高与胸径关系 [J].林业科学,2016,52(1):30-36.

Wang D Z,Zhang D Y,Zhang Z D,et al.Height-diameter relationship for conifer mixed forest based on nonlinear mixed-effects model [J].Scientia Silvae Sinicae,2016,52(1):30-36.

[13] 符利勇,李永慈,李春明,等.利用2种非线性混合效应模型(2水平)对杉木林胸径生长量的分析 [J].林业科学,2012,48(5):36-43.

Fu L Y,Li Y C,Li C M,et al.Analysis of the basal area for Chinese fir plantation using two kinds of nonlinear mixed effects model(two levels) [J].Scientia Silvae Sinicae,2012,48(5):36-43.

[14] Budhathoki C B,Lynch T B,Guldin J M.Nonlinear mixed modeling of basal area growth for shortleaf pine [J].Forest Ecology & Management,2008,255(8):3440-3446.

[15] 李春明,唐守正.基于非线性混合模型的落叶松云冷杉林分断面积模型 [J].林业科学,2010,46(7):106-113.

Li C M,Tang S Z.The basal area model of mixed stands ofLarixolgensis,AbiesnephrolepisandPiceajezoensisbased on nonlinear mixed model [J].Scientia Silvae Sinicae,2010,46(7):106-113.

[16] Hein S,Mäkinen H,Yue C,et al.Modelling branch characteristics of Norway spruce from wide spacings in Germany [J].Forest Ecology & Management,2007,242(2/3):155-164.

[17] 许 昊,孙玉军,王新杰,等.基于线性混合模型的杉木人工林枝条大小预测模型 [J].南京林业大学学报(自然科学版),2015(2):97-103.

Xu H,Su Y J,Wang X J,el at.Analysis of the branch size for Chinese fir plantation using the linear mixed effects model [J].Journal of Nanjing Forestry University(Natural Sciences Edition),2015(2):97-103.

[18] Fang Z,Baliey R L,Shiver B D.A multivariate simultaneous prediction system for stand growth and yield with fixed and random effects [J].Forest Science,2001,47(4):550-562.

[19] Zhao D,Wilson M,Bruce B E.Modeling response curves and testing treatment effects in repeated measures experiments: a multilevel nonlinear mixed-effects model approach [J].Canadian Journal of Forest Research,2005,35(1):122-132.

[20] 李春明.混合效应模型在森林生长模拟研究中的应用 [D].北京:中国林业科学研究院,2010.

Li C M.Application of mixed effects models in forest growth models [D].Beijing:Chinese Academy of Forestry,2010.

[21] 王少杰,邓华锋,黄国胜,等.基于哑变量的油松人工林和天然林生长模型 [J].森林与环境学报,2016,36(3):325-331.

Wang S J,Deng H F,Hang G S,et al.Dummy variables models inPinustabulaeformisartificial forest and natural forest growth [J].Journal of Forest and Environment,2016,36(3):325-331.

[22] 曾伟生,唐守正.非线性模型对数回归的偏差校正及与加权回归的对比分析 [J].林业科学研究,2011,24(2):137-143.

Zeng W S,Tang S Z.Bios correction in logarithmic regression and comparison with weighted regression for Non-linear models [J].Forest Research,2011,24(2):137-143.

[23] Pinheiro J C,Bates D M.Mixed effects model in S and S-plus [M].New York:Spring-Verlag,2000.

[24] Pinheiro J,Bates D,DebRoy S,et al.Linear and nonlinear mixed effects models [J].R Package Version,2007(3):57.

[25] 符利勇,唐守正,张会儒,等.基于多水平非线性混合效应蒙古栎林单木断面积模型 [J].林业科学研究,2015,28(1):23-31.

Fu L Y,Tang S Z,Zhang H R,el at.Multilevel nonlinear rmixed-effects basal area models for individual trees ofQuercusmogolica[J].Forest Research,2015,28(1):23-31.

[26] 肖 锐,陈东升,李凤日,等.基于两水平混合模型的杂种落叶松胸径和树高生长模拟 [J].东北林业大学学报,2015,43(5):33-37.

Xiao R,Chen D S,Li F R,et al.Simulating DBH and height growth trees for hybrid larch plantation with two-level mixed effect model [J].Journal of Northeast Forestry University,2015,43(5):33-37.