基本养老保险系统集成度的演化博弈分析及仿真研究

杨一帆，周伟岷

(1.西南交通大学公共管理与政法学院，四川 成都 610031;2.西南交通大学国际老龄科学研究院，四川 成都 610031; 3.巴塞罗那自治大学经济学院，西班牙 巴塞罗那 08119)

1 引言

在基本养老保险制度改革中，中央政府、地方政府和参保企业等利益相关主体对政策调整有不同的反应，从1991年国务院颁布《关于企业职工养老保险制度改革的决定》起，养老保险体系从“行业统筹”变为“地方统筹”之后，地区发展不平衡、劳动力流动障碍等多种原因使得统筹层次无法继续向全国统筹提升，造成各统筹地区基金结余状况苦乐不均，制度运行效率低。提高养老保险统筹层次，最终实现全国统筹，需要增强中央政府对养老保险的管理权利，且合理划分中央与地方对基本养老保险的筹资和支付责任，明晰事权与财权的界限，还要鼓励企业在获取利润的同时依照政策规定按时足额缴纳保费[1-2]。那么，如何刻画上述三者通过复杂互动最终达至提升统筹层次的政策目标呢？

当前学者们研究基本养老保险多是在假设基本养老保险服从现收现付制度的原则上，寻找参与者之间的最优化条件。例如，扩展代际交叠模型来描述含有养老保险的经济系统，得出养老保险福利与平均工资的最优比率及政府通过调养老保险税收水平来最大化总效用的情况，进而得出最优的养老保险费率或税率[3]。但这一路径存在难以逾越的约束：经典的个体模型讨论最优化，是通过加总最大化的个体效用来达到社会总效用最大化，进而找到唯一稳定的均衡点，然而，当从个体推移到总体时只能保证连续、零齐次和瓦尔拉斯定律，这三者却不能保证都得到理想中的均衡点。

此外，公共养老保险不同于其他公共服务产品，它更加难以保持不同代际间的协调同步。Hu Shengcheng[4]指出在现收现付体系下，预期投票的机会可能会使当前的纳税人表达出虚假的偏好。若青年和中年人对养老保险系统能否在他们退休时保持在适当水平没有任何期待，那么他们将不愿维持养老保险系统。Browning[5]通过假设只存在一次投票来处理这个问题，Hu Shengcheng[6]则假设选举发生于每一阶段并且之前的政策可以零成本更改来改进这一问题。Sjoblom[7]扩展了Phelps[8]重复投票环境下个体代际间连续存在的隐性契约这一开创性观点：投票发起人定立一项社会契约，其中隐含了一套奖惩系统。年轻的选举人由于自身也期望在老年时期获得相应的回报而同意将资源转移给当期的退休人员，否则会受到将来无养老金的惩罚。以上研究，提出隐性奖惩机制的存在保障了社会养老系统的运行，隐性契约成为养老保险研究的重要方向。然而，当执行契约放置在代际交叠模型中考虑时将不可避免的涉及博弈论，但博弈论的引入会引发结果高度的不确定性，在均衡方面也缺乏清晰的一致性。

基于以上认识，为了构建一个既能体现前文所提及的理论动态机制，同时描述基本养老保险系统中各主体之间复杂交互关系的模型，本文将结合投票理论和演化博弈论，从提高养老保险系统集成度这一目标出发，运用演化博弈模型及其模拟，并设计实验刻画中央政府、地方政府和企业三个利益主体的演化过程，为深化城镇职工基本养老保险改革、增强全国统筹力度提供决策依据。

2 模型设定

2.1 模型假设与描述

由于我国中央政府、地方政府和企业在参与养老保险系统方面已经形成各自相对独立的主体，在构建模型之前，本文提出以下假设来明确养老保险系统参与者的性质：

1)本文将政府划分为中央政府和地方政府并假设当前中国中央政府并非捕食者。(中央领导者在全国的财富体系中掌控着足够的共容利益)Olson[9-10]提出固定强盗逻辑，即无形的手可能会迫使利己主义的领导者做出利他主义的行为。一个流动的强盗因为不会收到下一期投资的残差，故不会顾及经济增长，同时在掌权期间内会榨取所有财富。相反，一个固定的强盗因其政体会存在得足够久而他将通过长期征税来获得之前投资政策的回报故在经济增长中会存在共容利益。据此，可以认为我国中央政府是以增长为导向的集权政府。

2)地方政府对于符合条件的企业而言是潜在的“捕食者”，通过调整养老保险的收益水平，地方政府能够影响企业的活动。这是因为地方政府不仅拥有主要的决策权，对于“捕食”有各自不同的偏好，还享受着由中央政府提供的信息优势。此外，我们还假设当中央政府对捕食有任何控制权时，“猎物”价值的提升将导致地方政府捕食数量的增加。

3)企业是潜在的“猎物”。一般而言，企业遵循

市场经济规律，但当前中国尚未完善的相关法律法规，产权不明晰，大量歧视性政策存在等问题使得企业对于“捕食”敏感。因此被捕食的“猎物”数量会随政策变化、体制改革等做出相应改变。

演化博弈模型能够更好地解释群体演化的动态选择过程，在许多研究领域得到了充分运用，例如，于涛和刘长玉[11]针对政府监管问题，构建政府与第三方两个主体关于产品质量监管的模型，王国红等[12]运用演化博弈模型分析中小企业的竞合与发展，张伟等[13]研究企业改革与社会福利之间的关系，高明等[14]和高宏玉[15]基于演化博弈理论研究环境污染与治理问题等，但当前鲜有文章研究养老保险系统中各主体的演化博弈过程。基于此，本文引入演化博弈模型来刻画养老保险系统中三个参与者的互动关系，依照Zhang Yongjing[16]的方法，改进的 R-M模型[17]设定为：

(1)

(2)

表1给出了模型中各变量的定义。

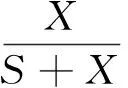
表1 变量描述

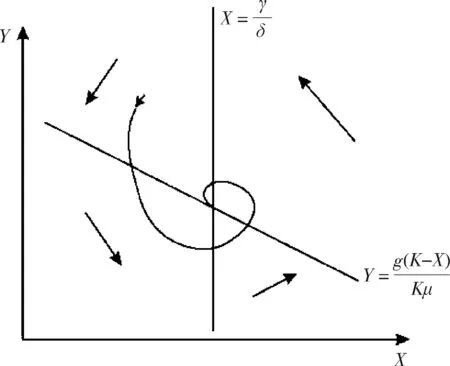
图1 猎物的逻辑增长

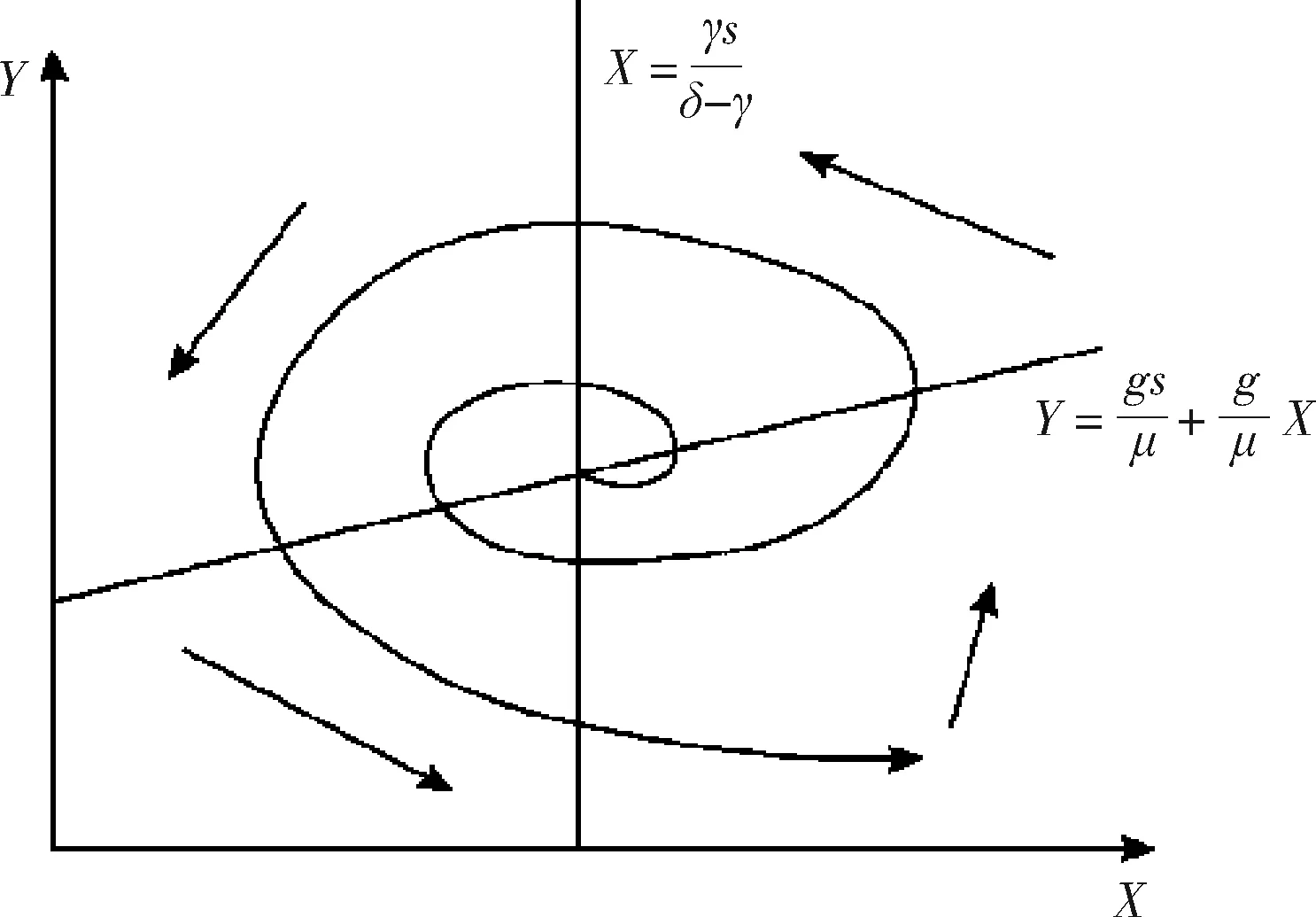
图2 将饱和度引入考虑

图3 将两个函数同时引入

图4描述了一个可导致猎物和捕食者灭绝的不稳定系统。当猎物轨迹的斜率大于0时，捕食者则过于高效，系统将不会正常地维持下去[18]。当猎物的最大密度，即该系统的承载量右移至临界峰值右侧后，猎物的富集将导致捕食者的过度开采，即“富食悖论”。当猎物密度的最大值为K时，X和Y轨迹的交点在临界峰值的左侧，进而演变为一个稳定的系统；但当猎物密度的最大值上升为K′时，交叉点则位于临界峰值右侧，导致猎物处于灭绝的风险。

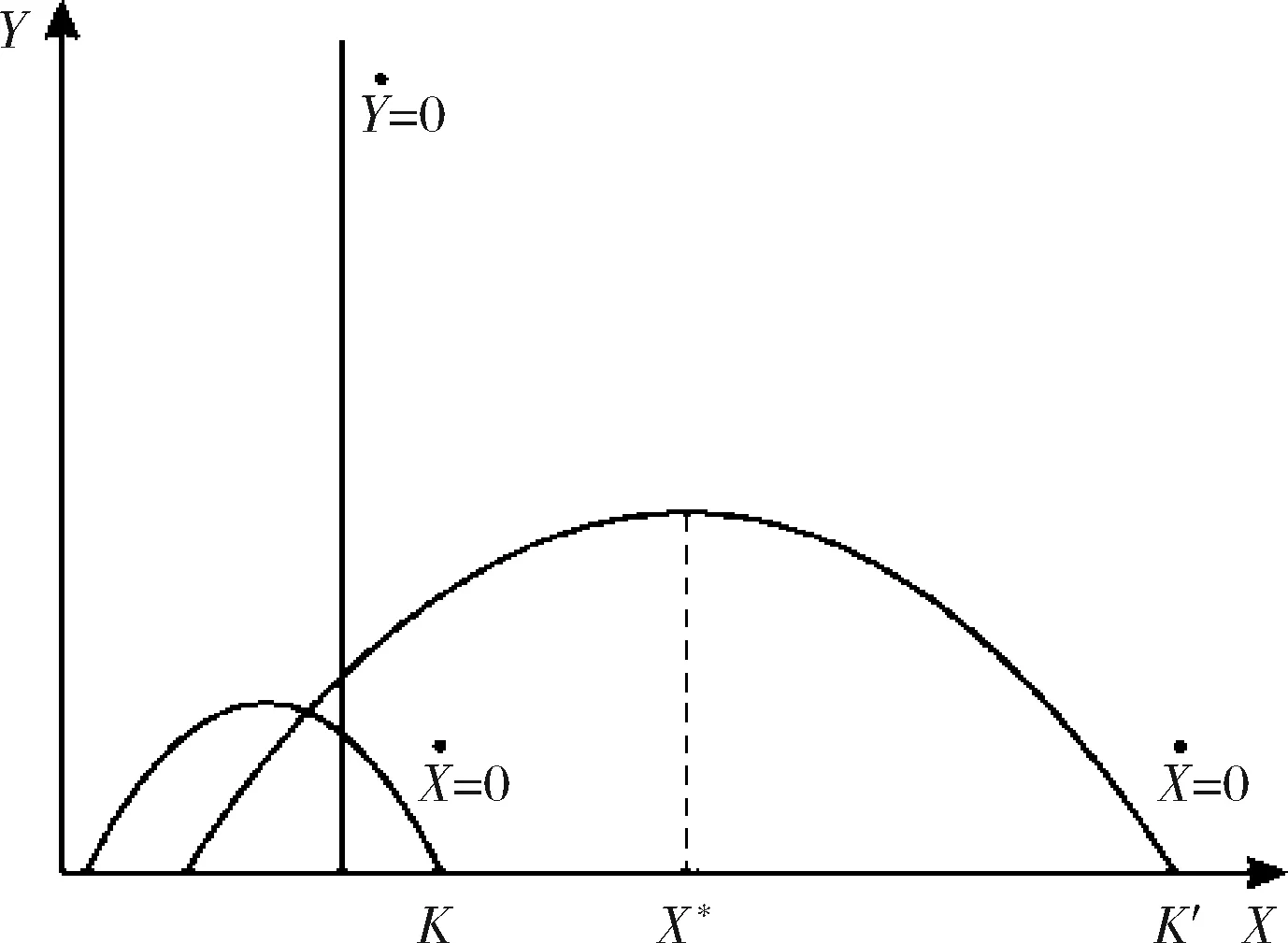
图4 R-M 模型中的富食悖论现象

分析R-M模型的含义之前，需考虑若中央政府打算提升整体水平时(即在保留或不保留地方养老基金的情况下设立国家养老保险系统)，养老保险替代率会如何变化。本文假设统一的国家养老保险系统带来的养老保险替代率不会高于富有省份以前的水平，同时也不会低于贫困省份以前的水平。由此，R-M捕食者—猎物模型的经济影响如下：

1)R-M模型表明总体水平的稳速增长较快速增长更有利。两个参数δ和γ在很大程度上决定了捕食者图像的位置。由于整个系统是受承载能力K约束的，故这一图像的移动应是稳速的而非快速的。若中央政府决定提升总体水平(即提升γ)但市场不能将承载能力调整到相应水平，就会造成不稳定的情况。图3中，若政府决定将捕食者图像往右移至与猎物图像无交点，那么政策便会失灵。另一种与整体水平相关的影响便是更高的总体水平(即更高的γ值)将使捕食者图像右移，这样不仅会增加猎物数量(即企业数量)，而且对经济有稳定作用。

2)更高的养老保险替代率，即更高的待遇充足水平会吸引更多移民，而这便会提升承载能力K。但是，这样也可能会造成被称为“富食悖论”的逆境。图4便描述了这一现象。随着承载能力从K上升到K′，临界值也相应上升。而临界值上升的结果则是捕食者图像将会坐落在临界值左侧，导致经济的不稳定。为避免这一情况，捕食者轨迹必须向右移动。在数理上有两个方法可行，增大S或减小δ。从政策制定的角度看，增大S意味着个体必须从其他地方获取比政府养老福利更多的资助。一个可行的办法则是鼓励商业保险机构更多地参与进来。而减小δ则意味着提升养老基金管理的效率。

3)参数g和μ对于经济的稳定性并无显著影响，因为捕食者与猎物间关系的稳定很大程度上取决于捕食者垂线的位置；其位置并不包含一些经济环境指标，如可能影响g和μ的保护私有财产权指标。但g和μ仍是影响轨迹循环程度的重要决定因素。例如，只考虑猎物的逻辑增长，猎物曲线的斜率为-g/μ。因此更好的经济环境会增加猎物曲线斜率的绝对值，如此也能快速压缩循环轨迹。

2.2 模拟仿真

为了探究城镇职工基本养老保险系统集成度(即中央政府对养老保费的集权化水平)、人口老龄化、养老保险管理效率和个体退休后收入多样性等变量对基本养老保险系统均衡的影响，我们通过调整γ、δ和S等参数，对R-M捕食者-猎物模型进行一系列模拟仿真。

在图5中，纵坐标表示福利水平的程度，横坐标则表示企业的密度，数值仅代表有序数。以福利程度=400，企业密度=600作为起始点开始模拟，如图所示，起初企业的密度增长至某一点，这时地方政府开始提高福利水平，之后企业的密度逐步下滑直到政府明显降低福利水平才停止。这个周期持续收敛至一个特定的点。

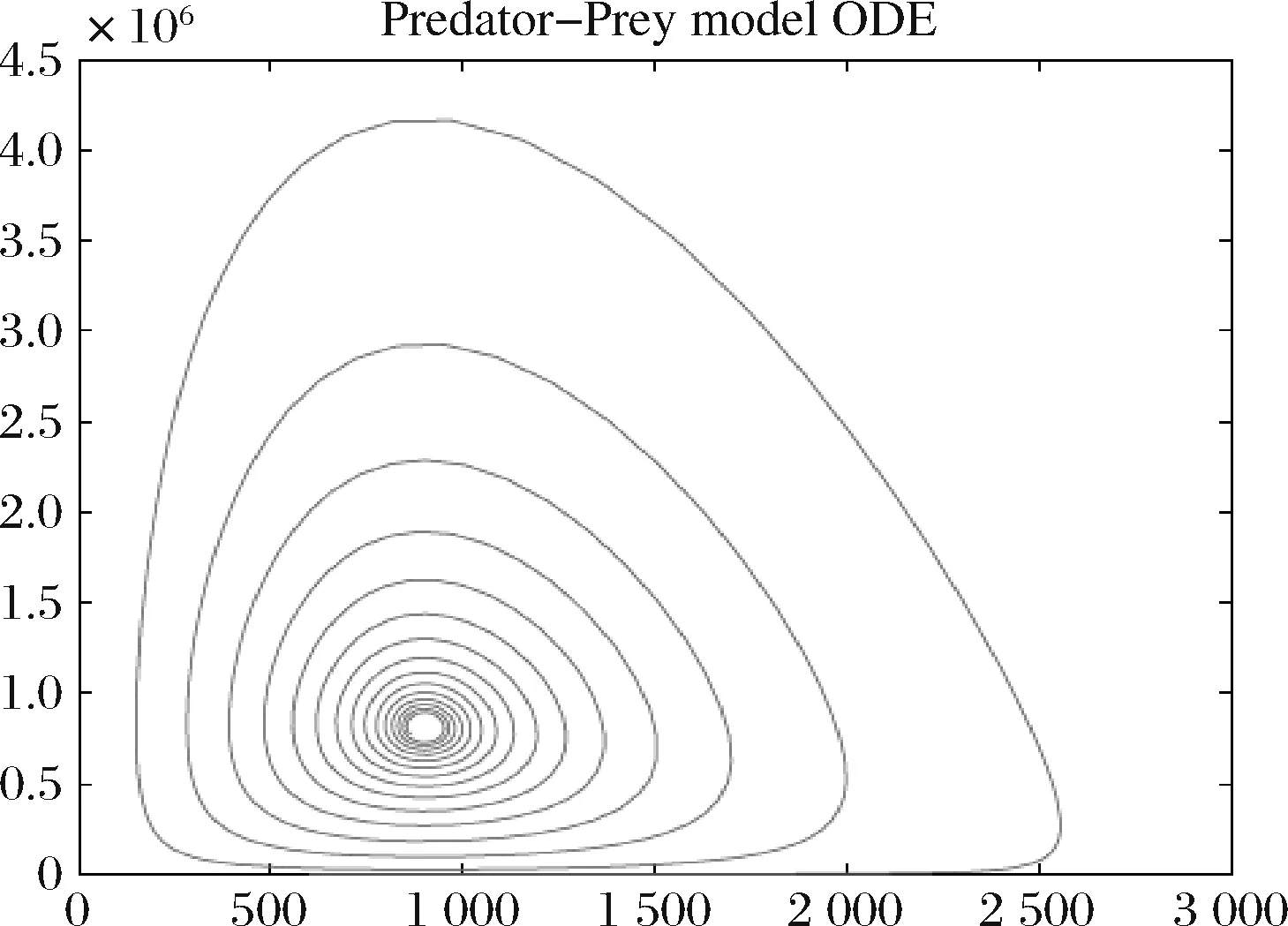
图5 捕食者—猎物模型，K=3000,S=2000,g=0.4,
μ=0.001,δ=0.001,γ=0.9

在只有人口持续老龄化而其他条件都不变时的情况下，由于X代表工作阶段人的密度，较低的g反映出人口的老龄化。如图6所示，系统经济依旧稳定，但工作人口的减少，显著增加了体系负担。简而言之，在人口老龄化导致养老保险体系负担系数较高时，有必要通过降低养老保险替代率来平衡账户[19]。

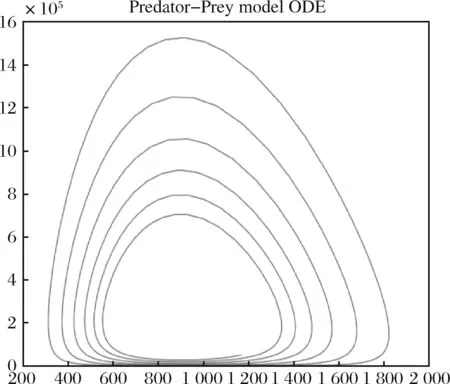
图6 保持其他参数不变，g=0.1

在图7中，γ的增加代表集成度的提升，模拟说明此时将更快地达到恒稳态，也将转化为更快的经济增长。这是因为更高的集成度暗示了统筹层次的提升和地区之间差距的缩小，进而促进劳动力更加自由地流动以及隐性成本的减少。同时这也带来了企业数量的增长，对欠发达地区而言也意味着养老保险替代率的提高，从而加速经济增长。此外，更高的集成度使地方政府制定养老保费的变化更小。

图7 保持其他参数不变，γ=2.0

δ是反映养老保险管理效率的指标，其值越低表明管理水平越高，因为这样下一期地方政府就能分配更多福利来提高养老保险替代率。如图8，若增大δ，即较低的养老保险管理效率，与图5相比，可以发现更低的管理效率意味着更慢的收敛速率[20]。

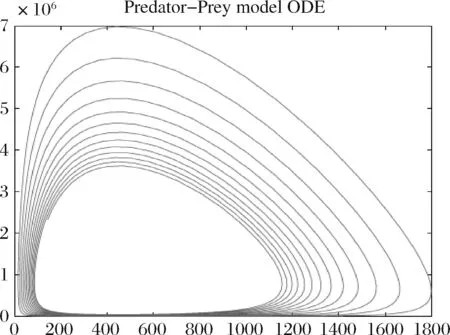
图8 保持其他参数不变，δ =0.002

S代表除基本养老保险计划外的其他资金来源，如商业养老保险或退休后特殊工作收入等。如前文所述，中央政府提升S值的一个可行办法是鼓励商业保险公司加入这一领域(发展养老保险体系第三支柱)，模拟结果(图9)反映出这一举措也能够加速经济的增长。这是因为政府养老保险福利受其覆盖范围和国家财政等限制无法进行过多支付，若退休后的收入来源受到限制，则退休后个体的消费能力也会受到限制。通过引入商业养老保险项目，个人在退休后则可拥有更高收入，进而通过增加消费实现经济的加速增长。

图9 保持其他参数不变，S=10000

3 实验设计与说明

3.1 实验设计

为刻画中央政府、地方政府和企业三个利益主体之间的动态博弈，本文设计含有集成式结构的中央政府和只有分散式结构中央政府的两个投票实验来探究三个重要主体就基本养老保险保费的博弈问题以及提升统筹层次的作用。

实验参与者分别扮演实验组织者，企业，地方政府和中央政府，后三者依据各自角色以利益为导向就基本养老保险的保费进行博弈，每次实验持续20轮，包含4名参与者，他们被随机划分以上四种角色并保持不变。

实验一

首轮实验前，企业的初始工厂数量为15，工厂数量为公共信息。在每一轮，实验组织者仅向企业代表展示企业当期的毛利润π (π为0～10之间的随机数)，仅向地方政府和中央政府代表展示企业当期毛利润可能所在区间(区间为当期毛利润加减0～5之间的随机数，若下界小于0则取0，上界大于10则取10)。之后，地方政府首先就基本养老保险保费向企业提出一个方案。若企业选择接受，则该方案为当期基本养老保险保费缴纳办法，企业按此缴纳保费给地方政府；如果企业选择不接受，则企业向中央政府提出一个方案(以上方案均为公共信息，所有实验参与者均需被告知)，中央政府从地方政府方案和企业方案中选择一个使之成为当期保费缴纳办法，地方政府和企业必须接受该办法，企业依据缴纳保费给地方政府，实验流程如图10所示。

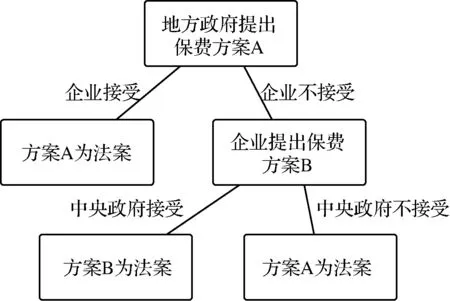
图10 实验一中最终保费的博弈过程

地方政府每期收益为:t*n，其中，t为每轮的最终保费，n为当期工厂数量，缴纳最终保费后，企业将从实验组织者处获得每个工厂进入下期的成本c(进入下期成本为企业当期毛利润乘以0～1之间的随机数)，企业的每期收益为：(π-t-c)*n，若企业的累计收益为正，企业根据盈亏情况，选择增减工厂数量并进入下一期，若累计收益为负，则实验结束。

实验一中的中央政府在每轮实验结束后的收益为：α*R+β*T，其中R为企业累计收益，T为结束时地方政府的累计收益，α和β为固定系数，实验组织者在实验开始前将仅向中央政府告知。

实验二

为了研究提升基本养老保险统筹层次的效果，本文在实验一的基础上加入了集成式结构的中央政府。此时的中央政府有两个责任，其一，中央政府须在地方政府提出缴费方案前，优先提出一个缴费方案，要求企业直接上缴方案所规定的保费给中央政府。但企业一旦接受该方案，则三轮之内不可更改方案内容，也不得撤销方案。其二，比照实验一，即在每一期实验，若企业接受地方政府方案，则中央政府无需任何动作；若企业不接受地方政府方案，并提出自己的方案，则中央政府需从地方政府方案和企业方案中二选一，实验流程如图11所示。

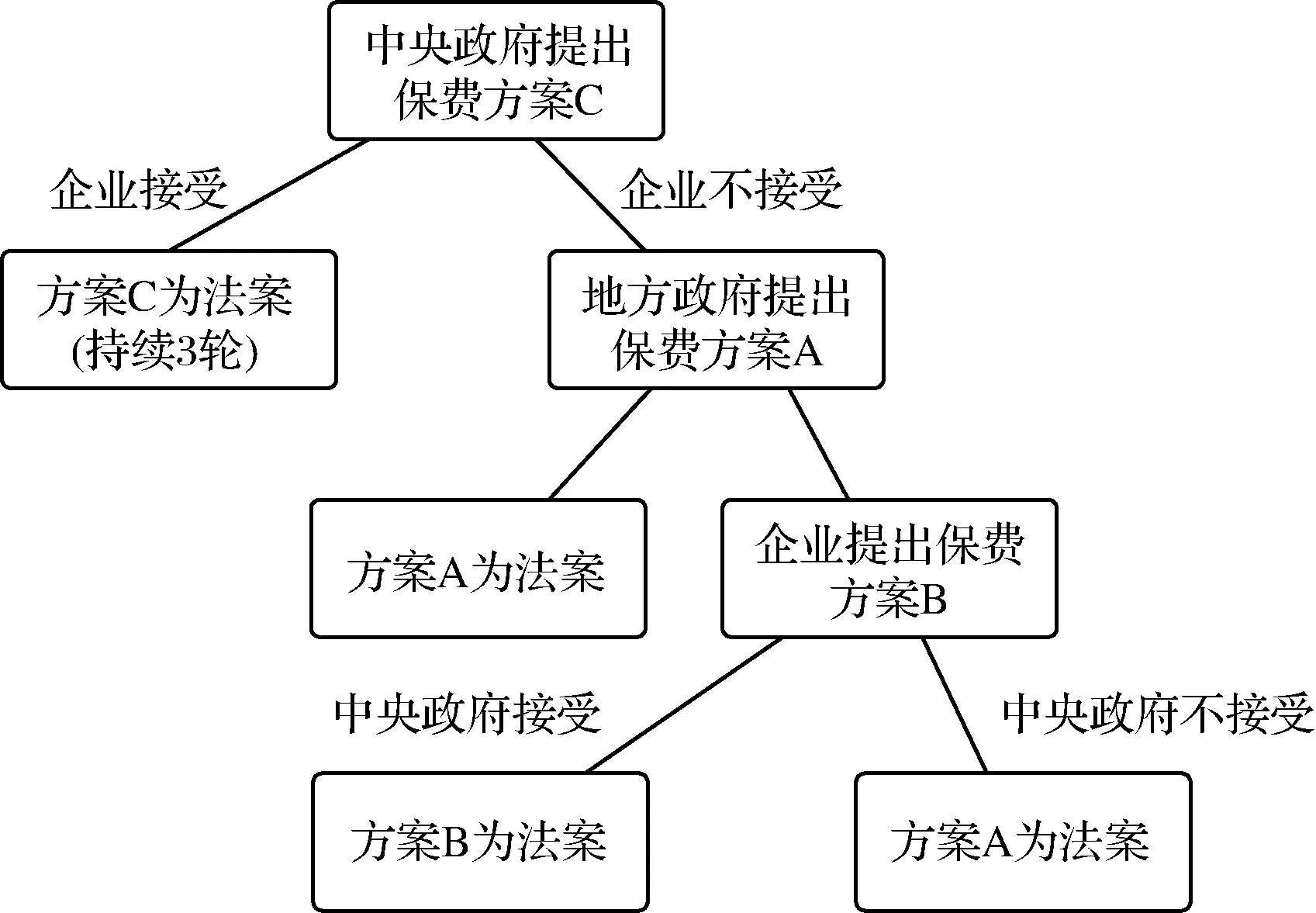
图11 实验二中最终保费的博弈过程

实验二的中央政府收益分为两部分，一是由企业直接支付的保费乘以当期工厂数量，二是在实验结束后，中央政府从地方政府征收的保费及从企业利润中征收的税费，其计算公式为：α*R+β*T+∑t*n。

3.2 实验过程

实验于2017年4月进行，共有48名社会保障专业的硕士研究生参加，他们均对基本养老保险制度和相关基础知识有了解，并提前在实验操作者的介绍和指导下熟悉了实验步骤；实验共有2个，实验一的中央政府为分散式结构，实验二的中央政府包含分散式结构和集成式结构两种。

在正式实验中，本文定义每轮实验初始工厂数量为15，α=β=0.3。企业为了最大化累计收益，需根据盈亏形势来调整其经营策略，选择增减工厂数量，具体增减数量由企业盈亏状况变化和企业家的风险偏好类型决定；地方政府则权衡企业的工厂数量和最终保费，以期达到利益最大化；中央政府需要兼顾地方政府收益和企业收益，实验二的中央政府方案是以地方政府与企业妥协共赢为目的而出现的，因而受以上两个因素共同影响。

3.3 实验结果分析

整理每组20个过程的博弈结果，可以计算出三个主体的累计收益，从而比较中央政府收益、地方政府累计收益和企业累计收益与平均保费之间的关系，如图12所示，运用局部多项式回归估计，得到三个博弈主体各自累计收益随平均保费的变化而变化。在实验一中，由于只存在分散式结构的中央政府：当企业不接受地方政府提出方案时，中央政府从地方政府和企业提出的两个方案中进行选择。因此，企业收益随保费增加而下降，适当的保费水平能使地方政府、中央政府和社会总收益达到最佳，但过低或过高的保费都会导致总收益下降。因而此时政府应保持适当的保费水平，从而保证较高的社会总收益。

图12 实验一各博弈主体累计收益随保费的变化

由于企业在博弈过程中不占优，当保费过高时，企业可以通过放弃工厂来退出养老保险制度，地方政府从而无法得到更高的收益，造成“富食悖论”。从图12中也可以注意到，在稳定系统中使得社会总收益最佳的保费更高，企业累计收益的水平较低。实际上，由于各地方政府与当期企业的博弈结果不同，不仅造成企业缴费的负担过高，还使各地区达成的最佳保费水平不一致，进而存在地区间难以协调的保费水平差异。那么，提升养老保险制度的统筹水平，从地方政府收缴上升为直接由中央政府收缴保费，是否能够增加企业数量，降低保费呢？为此，本文在实验二中加入了中央政府方案，中央政府除行使分散式结构时的权利外，还可以通过集成式结构来提升养老保险系统集成度水平，即直接向企业提出保费方案。

在实验二中，当含有集成式结构中央政府时，养老保险稳定系统收益最佳时的最终保费比实验一更低，企业拥有更多工厂数，累计收益更高，但地方政府累计收益更低，由于中央政府行使集成权力可以向企业直接收纳保费，中央政府累计收益得到了明显提升，如图13。

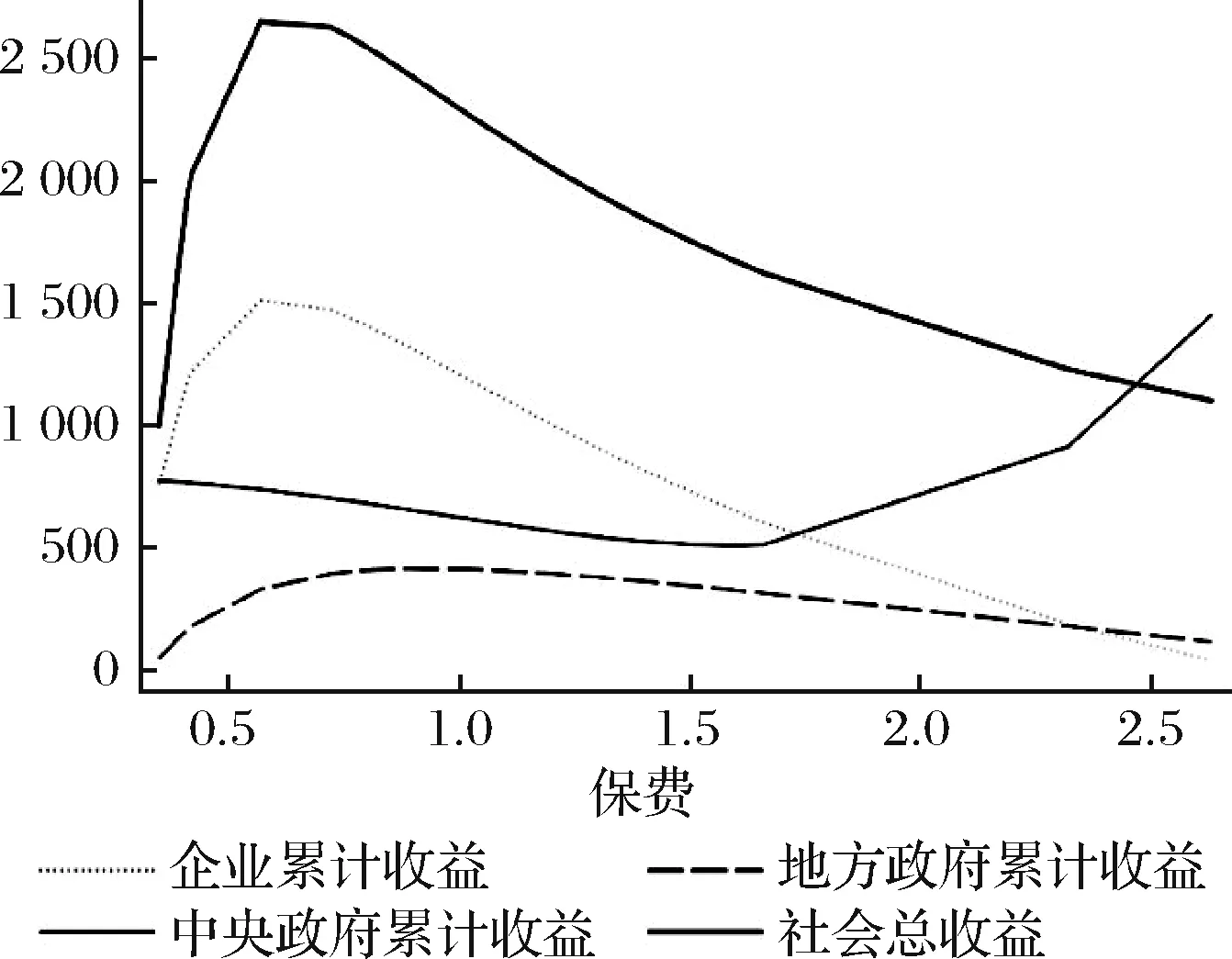
图13 实验二各博弈主体累计收益随保费的变化

实验二的结果与对集成度的模拟结果相一致，即由于加入中央政府方案，当企业接受中央政府直接提出的保费方案时，三轮过程之内保持保费不变，各主体对最终保费的博弈能更快地达到均衡。此外，如图14，中央政府行使集成权可以加速经济增长，但过多的集成次数超出了市场承载力，会降低集成结构的效果。

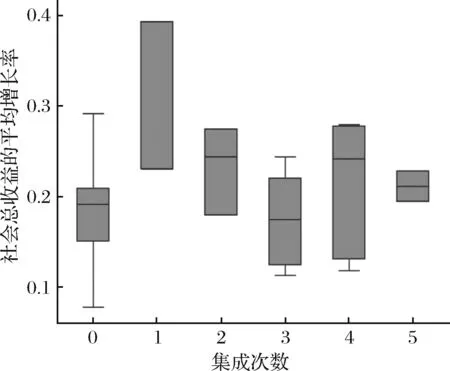
图14 社会总收益的平均增长率与集成次数的关系

4 结语

本文运用改进的R-M模型，将演化博弈理论引入养老保险系统的研究中，结合投票理论，规避传统效用最大化和博弈论方法的缺陷，通过定义基本养老保险系统集成度，探讨中央、地方政府与企业间的制衡，为基本养老保险系统持续改革提供决策依据。模型假设中央政府是以经济增长为导向的集权政府，地方政府为捕食者，企业为猎物，模拟分析表明提升养老保险系统的集成度水平能促进养老保险统筹层次的提高，还能促进经济增长。但过快的集成度进程会超出市场的承载能力从而导致政策的低效性。因此，中央政府应当稳速提升基本养老保险系统集成度，在逐步构建国家养老保险系统的同时给予地方政府和企业足够的时间来对这一改革做出相应调整。另外，提升基本养老保险的管理效率、强化收入替代、降低个体对基本养老保险的依赖程度，鼓励个体通过投资商业养老保险产品来获得退休后更多的福利支持，可以避免经济发展中因“富食悖论”而产生的不稳定波动。

基于对模型的分析，本文构建了投票实验，结果表明：提高系统集成度(即中央政府对养老保费行使集成权)能使系统更快达到均衡，提高养老保险管理效率、多样化退休后收入则可以提高个体退休后待遇充足性，实现经济增长。设计中央政府、地方政府和企业就最终保费进行博弈的实验，结果发现，中央政府行使集成权使得均衡保费更低并提高了社会总收益，但集成速度过快会降低社会总收益增长率。进一步的研究，可以探索养老保险系统对最终保费的演进稳定策略，考虑国有企业或地方政府的多重目标，以设计更细致的投票实验。

参考文献：

[1] 郭磊,苏涛永. 企业年金对养老保险差距的双重影响研究[J]. 公共管理学报,2014,(1):75-89.

[2] 杨方方. 我国养老保险制度演变与政府责任[J]. 中国软科学, 2005，(2):17-23.

[3] Auerbach A J, Feldstein M S. Handbook of public economics[M]. North Holland: Elsevier, 2013.

[4] Hu Shengcheng. On the dynamic behaviour of the consumer and the optimal provision of social security[J]. Review of Economic Studies, 1978, 45(3):437-445.

[5] Browning E K. Why the social insurance budget is too large in a democracy[J]. Economic Inquiry, 1975, 13(3):373-88.

[6] Hu Shengcheng.Social security, majority-voting equilibrium and dynamic efficiency[J]. International Economics Review,1982,23(2):269-287.

[7] Sjoblom K.Voting for social security[J]. Public Choice, 1985, 45(3):225-240.

[8] Phelps E S.Altruism, morality, and economic theory[M].New York: Russell Sage Foundation, 1975.

[9] Olson M. Dictatorship, democracy, and development[J]. American Political Science Review, 1993, 87(3):567-576.

[10] Olson M. Power and prosperity: Outgrowing communist and capitalist dictators[M]. New York: Basic Books, 2000.

[11] 于涛, 刘长玉. 政府与第三方在产品质量监管中的演化博弈分析及仿真研究[J]. 中国管理科学, 2016, 24(6):90-96.

[12] 王国红, 刘隽文, 邢蕊. 竞合视角下中小企业协同创新行为的演化博弈模型研究[J].中国管理科学, 2015,23(S1):662-666.

[13] 张伟, 仲伟俊, 梅姝娥. 基于差异产品的外资渗透、私有化程度与社会福利研究[J]. 中国管理科学, 2016, 24(11):11-18.

[14] 高明, 郭施宏, 夏玲玲. 大气污染府际间合作治理联盟的达成与稳定——基于演化博弈分析[J]. 中国管理科学, 2016, 24(8):62-70.

[15] 高宏玉. 基于前景理论的水污染事件防治行为演化博弈[J].中国管理科学, 2015,23(S1):853-859.

[16] Zhang Yongjing. China's evolution toward an authoritarian market economy—a predator-prey evolutionary model with intelligent design[J]. Public Choice, 2012, 151(1):271-287.

[17] Rosenzweig M L, Macarthur R H. Graphical representation and stability conditions of predator-prey interactions[J]. The American Naturalist, 1963, 97(895):209-223.

[18] Rosenzweig M L. Paradox of enrichment: Destabilization of exploitation ecosystems in ecological time[J]. Science, 1971, 171(3969):385-387.

[19] 谢安. 改革现行养老保险体制应对人口老龄化[J]. 管理世界, 2005,(4):34-34.

[20] 郝勇,周敏,郭丽娜. 适度的养老保险保障水平:基于弹性的养老保险替代率的确定[J]. 数量经济技术经济研究,2010,(08):74-87.

[21] 柳清瑞. 养老保险替代率的自动调整机制研究[J]. 中国人口科学,2005,(03):51-55.

[22] 贾洪波,温源. 基本养老保险替代率优化分析[J]. 中国人口科学,2005,(01):81-87.

[23] 杨立雄,何洪静. 中国城镇职工基本养老保险管理体制创新研究[J]. 中国软科学, 2007,(3):45-52.

[24] 邓晓辉, 李好好. 中国养老保险制度改革的短期政策选择[J]. 中国管理科学, 2002, 10(s1):467-470.