考虑需求波动的单元装配系统构建问题的多目标模型

王 晔，唐加福，赵林度

(1.东北财经大学管理科学与工程学院，辽宁 大连 116025；2.东南大学经济管理学院， 江苏 南京 210096)

1 引言

在全球经济一体化的过程中，制造业的发展扮演着不可或缺的角色。根据德勤公司的2016年全球制造业竞争指数调查的结果显示，制造业对全球的经济发展都起到了关键带动作用，包括基础设施提升、增加就业岗位、对全民GDP以及人均GDP的贡献率等[1]。随着人工智能和高新技术与民用产品的结合，当今市场呈现对产品智能化、多样化的更高需求。在市场需求的变化下，生产制造企业在应对多品种、小批量且生命周期短的产品生产过程中面临巨大的考验，并不断探索应对方式。例如通过供应商和制造商之间的订单分配[2]，平衡生产和库存[3-4]以及协调制造商和销售商[5]等方式实现总体利润最大化，与此同时，制造企业内部生产流程的优化也是提升企业整体竞争力的重要环节。

日本制造企业在20世纪80年代的经济大发展时期由于需求的迅速增长，引进了大批的生产线设备进行大规模生产。然而，90年代经济泡沫破灭的连锁反应导致日本制造业面临前所未有的挑战。由于市场对产品的需求转变，原有的流水线生产方式明显无法应对高技术附加值、生命周期短等特点的产品生产，日本式单元制造模式应运而生[6-8]。日本式单元制造系统(Seru production system)是由以佳能、索尼等日本电子装配业公司的不断探索实践中总结出来的一种先进生产组织方式。它融合了西方传统单元制造、日本精益生产和敏捷制造等生产模式的特点，兼备流水线的高效性、传统单元制造的灵活性以及精益生产的低成本，以应对多品种、中小批量，特别是变批量的生产方式[7-10]。Seru是日语中英文单词cell的发音，源于西方传统单元制造(Cellular manufacturing)中的cell一词。Seru是指为完成一个或多个产品的组装，由一个或多个员工和一些设备组成的一个装配单元，主要实现形式为以装配单元取代原有的传送带，即流水线装配向单元装配的转换[9]。

有关日本式单元装配系统的研究由日本的企业界和学者最先总结归纳[11-12]，并得到了各国学者的广泛关注[7-10]，其中日本式单元构建研究成为研究的重点[13-21]。Kaku等[13]最先提出以最小化总产出时间和总加工时间为目标，构建流水线装配和单元装配混合系统的多目标优化模型，以数值仿真的方法验证模型的有效性并分析了产品种类、批次数量、批次大小以及任务规模对目标函数的影响。Liu Chenguang等[16]考虑由流水线装配向单元装配系统转换过程中的工人培训成本，以最小化培训成本和加工周期为目标进行单元系统的构建。Yu Yang等[17-21]对流水线装配向纯单元装配系统转换的问题进行研究，以最小化总加工时间和最小化工人加工时间以及以减人为目标建模。以上研究的一个共同点是，针对(每天)特定的生产任务(包括产品种类和数量)，在流水线向单元装配转化的生产场景下，给出相应的单元装配系统(混合单元装配线或纯单元装配线)以及生产调度方案。这种单元装配系统的好处是，柔性好，针对任何不同的生产任务(需求)，产品种类和批量大小，均能适应的装配单元系统；然而，该系统的缺点是，由于现实需求的波动(包括产品种类和批量大小)和不稳定，制造企业需要频繁进行生产系统的构建，这样不仅造成资源闲置和浪费(如新添置工作平台、辅助性的移动设施和工具等)，而且单元内部的人员频繁调整，合作不稳定，生产效率受到相应影响。另外，在实际的制造企业中，频繁调整生产线也不容易被接受。Yu Yang等[17-21]虽然提出生产任务的批次种类和批次大小按照相应规律随机生成，但在优化的过程仍是按照已知的任务进行。利用现有的研究成果进行单元系统的构建会产生较高的单元系统重构成本以及工人频繁变动引起的工人满意度下降、管理成本过高等问题。因此，在既要保证系统柔性，同时兼顾效率和稳定性，考虑面向一定周期的单元装配系统的构建具有十分重要的现实意义，不仅丰富和发展单元系统构建的理论，而且也为生产管理者提供更为贴近现实生产环境的单元构建方法。

针对这一不足，本文的主要贡献是讨论需求波动情境下的流水线装配向单元装配系统的转换问题。总加工周期(Make span)的大小直接关系到产品的交货期，通过缩小总加工周期可以直接提升企业在动态多样化的市场上的竞争力。因此本文为避免由于需求波动引起的单元系统重构成本，通过建立考虑需求波动的流水装配向单元装配系统转换方案，决策需要构建的装配单元的数量、工人与装配单元之间的分配方式以及产品批次向单元的分配方法，构建需求波动情境下最小化总加工周期的期望和方差的单元构建多目标优化模型。其中最小化总加工时间的期望值和方差值分别是为了使系统能在需求波动的场景下具备较好的期望性能和较为稳定的表现。任务确定型的流水线装配向单元装配系统转换问题已在文献[18]中被证明为NP-hard问题，不存在多项式时间内求得最优解的精确优化算法。本问题由于考虑了需求的波动性而比原问题更为复杂，因此需采用有效的启发式优化算法对问题进行求解。NSGA-II(Non-dominatedsorting genetic algorithms)算法作为求解多目标优化问题的启发式算法在收敛速度和解的多样性方面均表现出较好的性能，是目前综合性能较好且应用较为广泛的多目标优化算法。本文针对模型的特点采用基于NSGA-II的算法对本问题进行求解，并通过数值实验说明模型和方法的运用规则和相关性质。

2 问题描述与模型建立

2.1 问题描述

Stecke等[9]提出日本式单元装配系统中的单元(Seru)按照理想程度被分为分割式单元(DivisionalSeru)、巡回式单元(RotatingSeru)以及单人单元(Yatai)，其中最理想的状态为单人单元，即每名工人独立组成一个单元，可以直接通过增减单元的数量来应对产品需求的变化。但在实际企业的应用过程中，由于考虑到构建单元的成本及工人在工作中的互相交流等问题，多采用分割式单元和巡回式单元。

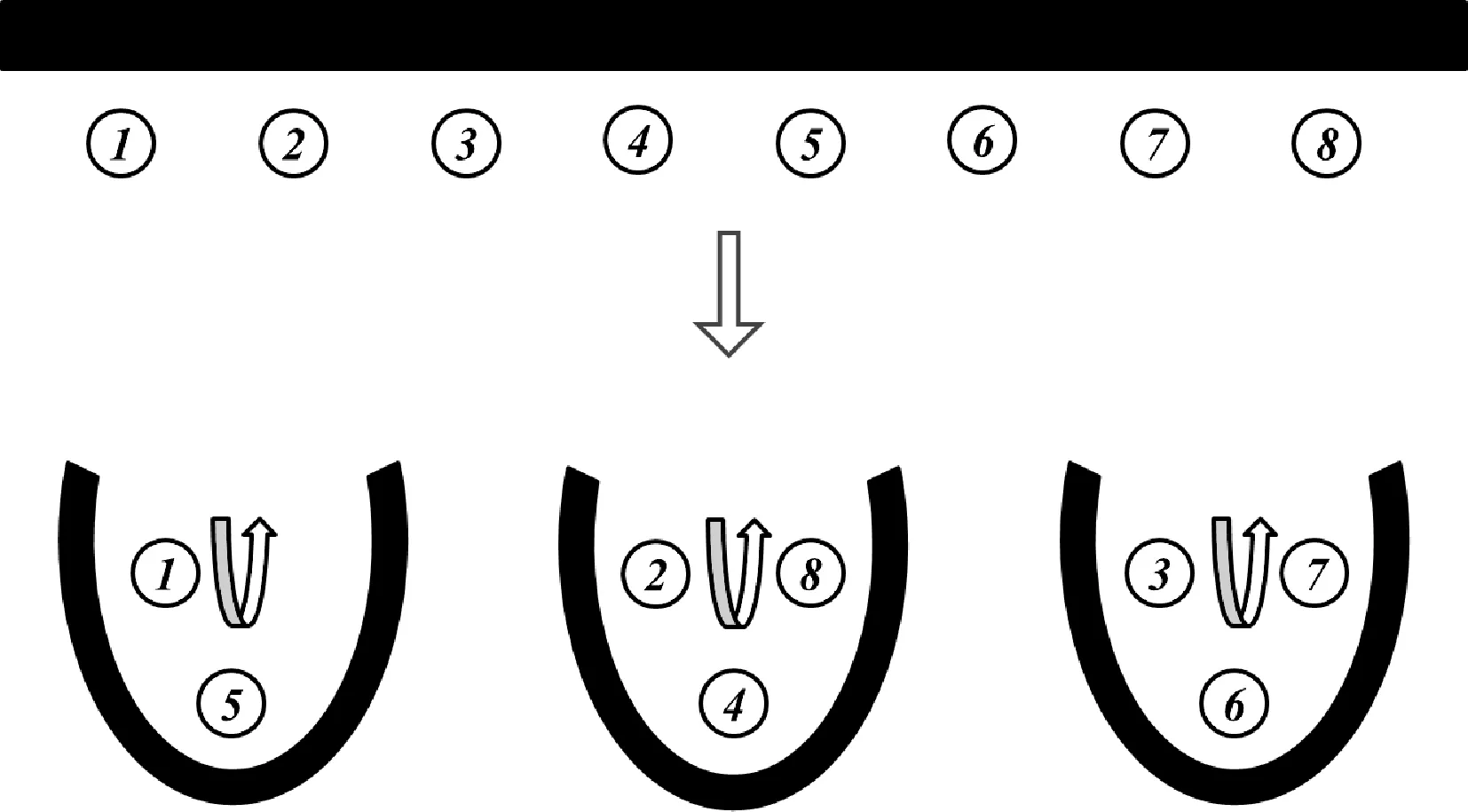
图1 流水线装配向单元装配转化(8名工人)

本文采用巡回式单元作为构建单元装配系统的基本单位，即分配到单元内的每一名工人独立完成所有类型产品所有工序的装配。当多名工人分配到同一个巡回式单元内时，员工各自按顺序完成所分配产品的全部工序，因此巡回式单元也被称为逐兔式单元。由8名工人组成的流水装配线转换成巡回式单元系统的转换方式如图1所示，原流水线上完成第2、4和8号工序的工人被分配到单元2中。

本文考虑在一个需求波动的环境下存在S种需求场景，第s种场景出现的概率为ps，∑ps=1。每种场景下的需求均为N种产品的不同批次组合，每种场景会有M个批次且每个批次只有一种产品类型。在此生产环境下，设计由W个工人组成的流水装配线向纯单元装配转换的构建方案。在生产系统中所有工人均为多能工，即可以独立完成任何一种产品类型的全部装配操作且全部分配到各个单元中。流水线装配的节拍时间T、完成第n种产品的各工序l的标准加工时间Tnl(Tnl≤T)以及工序的先后关系已知。单个批次的产品全部分配到同一个单元内进行加工且批次不拆分。由于工人全部为多能工，每个单元都具备完整加工任何类型产品的能力，因此不存在产品的单元间移动。系统中的基本单位均为巡回式单元，分配到每个单元内的工人数可以不同。通过决策构建单元的数量、每个单元内分配的工人数量以及每种场景下各批次与单元的分配方案，构建最小化总加工周期的期望和方差多目标优化模型。总加工周期期望值最小化可以减小生产的期望交货期，在需求波动环境下提升企业的竞争能力；最小化加工周期的方差保证了在需求变动的环境下系统的稳定性，不会因为需求的波动而造成加工周期的变动幅度过大。每种场景下的批次之间均采用先到先服务(FCFS, First come first service )的调度方式，按照批次顺序依次分配到第一个空闲的单元当中，如果没有空闲的单元就分配到预计最先完成加工的单元中。由8个批次组成的生产任务分配到三个单元中的FCFS调度方案如图2所示，矩形条内的数字代表批次到达的顺序，矩形条的长度代表该批次的加工时间。

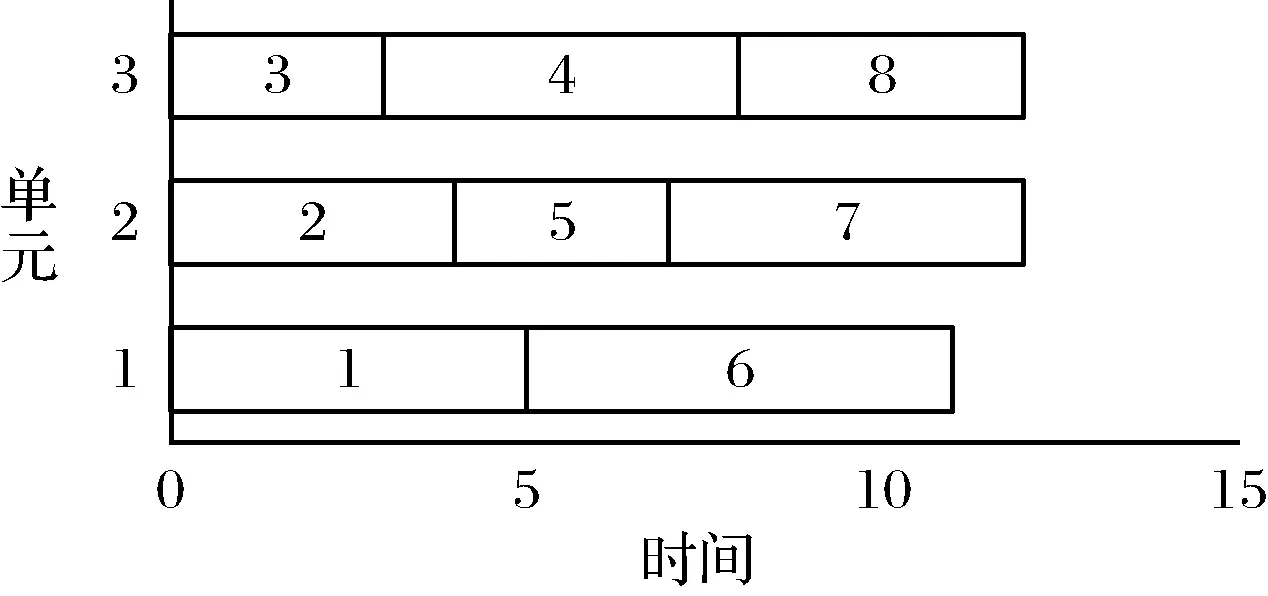
图2 FCFS调度方式实例

2.2 模型建立

模型参数：

L为原有流水线上的工作站即工序的数量，每个工序由一名工人进行操作，总工人数为W，l为工序的索引号，i为工人的索引号，i=1,2,…,W，l=1,2,…,L，W=L；

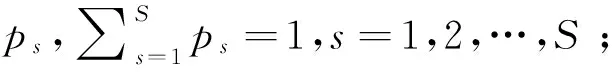
N为生产任务中产品的种类数，n为产品类型的索引号，n=1,2,…,N；

M为每种情境下的批次的个数，m为批次顺序的索引号，m=1,2,…,M；

Vmns=1表示在情境s下的第m个批次的产品类型为n，否则Vmns=0；

Bms为在情境s下的第m个批次的产品数量；

Tnl为第n类产品的第l个工序的标准加工时间；

γil表示工人i对工序l的操作熟练程度；

Stn为第n类产品在单元内的生产准备时间；

SLn为第n类产品在流水线上的生产准备时间；

决策变量：

J为构建单元的数量，1≤J≤W；

Xij为工人分配方案的0-1决策变量，工人i分配到单元j中，Xij=1，否则Xij=0，i=1,2,…,W；j=1,2,…,J；

Zmjks为s情境批次与单元分配方案的0-1决策变量，在情境s下第m个批次以第k个顺序被分配到单元j中则Zmjks=1，否则Zmjks=0，m=1,2,…,M，j=1,2,…,J，s=1,2,…,S，k≤M。

本文研究的流水线装配向单元装配的转换问题中，工人原有的工作为流水线上的某一道工序。对于原有L个工序和W个工人的流水线向单元装配转换问题，在培养流水线单序工人成为全能工的过程中，由于工人学习能力和自身工作经验等原因，工人i对工序l的熟练程度是不同的，以γil≥1表示。γil越接近1时工人i对工序l的操作熟练程度越高，反之γil的值越大表示工人对该工序的熟练程度越低。因此工人i完成第n类产品第l个工序的加工时间为Tnl*γil。在情境s下第m个批次中的单个产品在所分配的单元j中的操作时间TTms如式(1)所示，第m个批次全部产品完成加工的时间TF如式(2)所示。

(1)

(2)

对于每类产品在进行生产之前都需要进行生产环境的重设置，产生生产准备时间。生产过程中，每个单元生产产品的前后两批次产品类别不同时便会产生生产准备时间，当前后加工的两个批次为相同产品类型时则准备时间为0，在情境s下第m批次的生产准备时间TSms如式(3)。第m批次的开始加工时间TBms为上一个批次完成的时间，如果第m批次为所分配单元的第一个进行加工的批次，则开始时间TBms为0，具体表达如式(4)所示。在此基础上，情境s下的总加工时间Make span以该单元装配系统中最后一个完成生产任务的单元总完成时间表示，表达式如式(5)所示。

{(j,k)Zmjks=1,∀j,k}

(3)

(4)

(5)

考虑需求波动的流水线装配向单元装配系统转化最小化Make span均值和方差的多目标模型为：

(6)

(7)

(8)

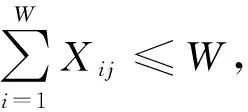
(9)

(10)

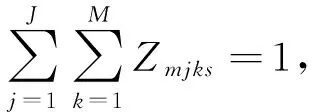
(11)

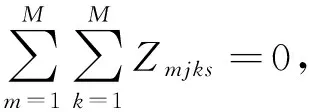
(12)

m=2,3,…,M,∀s

(13)

1≤J≤W

(14)

Xij,Zmjks∈{0,1},∀i,j,k,s

(15)

目标函数式(6)表示最小化各种可能情境下的总加工周期的期望值；目标函数式(7)表示最小化各种可能情境下的总加工周期的方差；约束式(8)表示每名工人只能被分配到一个单元内；约束式(9)(10)表示分配到任一单元内的工人数不超过原有流水线上的总人数，且所有工人都分配到了单元系统当中；约束式(11)表示在任一情境下的每个批次都会被分配也只能被分配到一个单元中，且不能被拆分；约束式(12)表示所有的批次都不会被分配到没有工人的单元内；约束式(13)表示任一情境下的各个批次都要按序进行分配，保证FCFS的调度规则；式(14),(15)是决策变量的取值范围约束。

3 算法设计

本文提出的流水线装配向单元装配转化问题的模型属于多目标优化问题。考虑一个简单的情景，当s=1时，本问题转换为确定性任务的日本式单元构建问题，该问题在Yu Yang等[18]中已经证明为NP-hard问题。因为本问题中s≥1，复杂程度更高，所以本问题也是NP-hard问题，不存在多项式时间内求得最优解的精确算法。对于多目标问题的求解，一般使用加权重的方式将多目标问题转化为单目标问题进行优化求解，但权重方法本身存在求解的劣势[22]。首先多目标之间存在相互制约，如何确定加权系数对问题最终的求解存在较大的影响。其次，由于多目标的帕累托最优集存在多个最优解，运用简单加权重的方式只能求得单个最优解而无法求得全部最优集[22]。针对这一问题，多目标启发式算法成为解决多目标优化问题的主要方法[23-25]，如多目标差异演化算法(Multi-objective differential evolution，MODE)[23],帕累托获取演化策略(Pareto archived evolution strategy，PAES)[24]，NSGA-II[25]等。在这些多目标优化算法中，NSGA-II算法的应用较为广泛并且在各类问题中都表现了很好的准确性和高效性[18, 25]，特别是对多目标帕累托前沿的获取。因此本文根据所研究问题的特征，选择使用基于NSGA-II的优化算法进行求解。

NSGA-II算法是在遗传算法的基础上引入了非支配排序和拥挤距离来评价多目标优化解的优劣，在求解的收敛速度和解的多样性保留方面均表现出较好的性能，是目前综合性能较好且应用较为广泛的多目标优化算法。NSGA-II延续了GA算法在种群的交叉遗传变异以及子代种群的产生方面的思路，但是在具体的个体优劣的评价和适应度的计算方面却有很大的区别。本文的目标函数有两个，分别为：总加工周期的期望和方差。在基于NSGA-II的优化算法中运用非支配排序和拥挤距离评价解的适应值，并进行解的选择。在两个解的对比中，若其中一个解的两个目标函数值均优于第二个解或第一个解的一个目标值优于第二个解而另一个目标值相等时，称第一个解占优于第二个解，或称第一个解支配第二个解。对所有的解进行非支配排序，占优级别越高的解具有更小的级别编码。当非支配级别相同时，为了保证种群中最优解的差异性，更好的解指的是在两个解当中，拥挤距离较大的一个解。拥挤距离是指在解空间中，两个解之间的欧氏距离。结合多目标解的评价机制的同时，运用GA来进行每一代种群的选择、交叉和变异等操作，最终选定最优解的组合。结合本问题的特征，在染色体编码、交叉与变异算子的选择和操作方法上都进行了相应的调整。

3.1 染色体编码

本文目的为求工人组成单元系统的构建方案，因此每条染色体以工人和单元的对应关系为描述对象，采用顺序编码的方式进行编码。对于W个工人的流水线向单元转换的问题中，采用1到2W-1的数字来编码，小于等于W的数字代表工人，大于W的数字代表分割数，以此编码表示工人与单元的对应关系。例如染色体“7264513”表示一个由4名工人的流水线装配向单元装配转化问题中的一个构建方案。其中大于4的数字代表分隔符号，小于等于4的数字代表待分配工人的编号，该染色体表示系统共分割为3个单元，工人2分配到第一个单元，工人4分配到第二个单元，工人1和工人3分配到第三个单元。

3.2 交叉与变异

为了适应本文的编码方式，确保交叉运算后染色体的可行性，本文选择了Davis[26]提出的两点顺序交叉法进行交叉运算。例如染色体1“7264513”和染色体2“3142657”进行交叉运算，采用两点顺序交叉法得到的运算结果为子染色体1“1 2 |6 4 5 |7 3”和子染色体2“7 5 |4 2 6| 1 3”，具体交叉运算的步骤参考Davis[26]。运用该交叉方式可以满足染色体的可行性，免去对染色体调整所产生的运算复杂性。

在变异运算中，针对本问题的特征采取随机选择两点元素互换的方式进行。例如染色体“3142657”进行变异运算，将在染色体中选择随机的两点进行，变异结果为“3642157”。通过两点互换的变异操作可以更改原有单元构建方案中工人的分配方式或者构建单元的数量。该变异方式可以在保证个体可行性的同时丰富解的多样性。

3.3 精英保留策略

每一次迭代根据规模为N的父代种群Pi生成与父代种群规模一致的子代种群Qi，将Pi和Qi合并。由于问题特殊性，编码规则的特征会导致不同染色体编码得到同样的解码结果，例如“7264513”和“6 2 5 4 7 31”两个个体的编码不同，但解码结果是一样的。为了避免优化进入局部最优解，首先将并集进行重复性剔除，即剔除解码相同的个体。在此基础上，运用锦标赛法对全部个体进行非支配排序，按照种群内个体的优劣程度选择最优的N个个体作为新一代的父代种群Pi+1。

3.4 算法步骤

基于Deb等[25]提出的NSGA-II算法，针对本文研究问题的特点，运用的算法步骤如下：

步骤1：随机生成规模为N的初始种群P0；

步骤2：将种群内的个体解码并计算每个个体的各分目标的目标值和适应值；

步骤3：对种群内的个体进行非支配排序和拥挤距离的计算，并按优劣程度排列个体；

步骤4：通过交叉和变异等操作进行GA的运算，生成规模为N的后代种群Q0；

步骤5：将P0和Q0合并为规模为2N的种群P0∪Q0；

步骤6：对P0∪Q0进行解码重复个体的剔除操作；

步骤7：将种群内的个体解码并计算每个个体的各分目标的目标值和适应值；

步骤8：对种群内的个体进行非支配排序和拥挤距离的计算，并按优劣程度排列个体；

步骤9：按序选择最优的N个个体作为新的父代种群P1；

步骤10：重复步骤4到步骤9，直至到达最大迭代次数；

步骤11：输出最终非支配排序解。

4 数值检验分析

4.1 基本算例

上述算法用MATLAB语言编程实现，并在Intel(R) Core i5内存8G的计算机上进行了大量的数据检验计算，取得了较好的效果。下文给出一个具体的算例来说明模型和算法的应用。基于前文提出的考虑需求波动的流水单元转换模型，本文以Yu Yang等[18]提出的Benchmark数据为例，来验证本文提出的模型和算法的效果。由于Yu Yang等[18]的研究没有考虑需求波动的因素，本文在原问题的基础上，对参数进行扩充来适应动态需求场景下的单元系统构建问题。在本文中，假设有5种可能出现的场景，各种场景出现的概率和为1。在一条由6道工序组成的流水线上有6名工人完成5种不同产品的装配。针对每个可能出现的场景随机生成25个批次的生产任务，每个批次内由单一种类的10件产品组成，产品种类随机生成，具体数据如表1所示。表1中的每一列代表可能出现的场景中批次的信息(产品编号)以及可能出现的概率，例如第1列表示场景1中第一个批次是产品类型5，第二个批次是产品类型3，以此类推。最后一行代表5个场景发生的概率分别为0.1，0.4，0.2，0.1，0.2。流水线装配的一个显著特点是各工序的操作时间小于等于流水线的节拍时间，假设原流水线的节拍时间为1.8分钟，而第n类产品的第l个工序的操作时间Tnl在区间[1.4,1.8]上随机产生，如表2所示。表中每一行代表不同产品类型，每一列代表产品加工的工序，例如表中第2行第3列表示第2类产品第3个工序的标准加工时间为1.6分钟。由于先前的工作经验等原因，不同的工人对每道工序的熟练程度γil不同，γil≥1表示工人i对工序l的熟练程度。γil越接近1时工人i对工序l的操作熟练程度越高，反之γil的值越大表示工人对该工序的熟练程度越低。具体数值如表3所示，例如第1行的第4列代表工人1对工序4的熟练程度为1.05，因此如果由工人i操作第n类产品的工序l时装配时间为Tnl*γil。当单元生产的前后两个批次为不同种产品时会产生生产准备时间，由于产品类型的不同，准备时间不完全一致，具体如表4所示，每行为该类产品在单元内和在流水线上的生产准备时间。

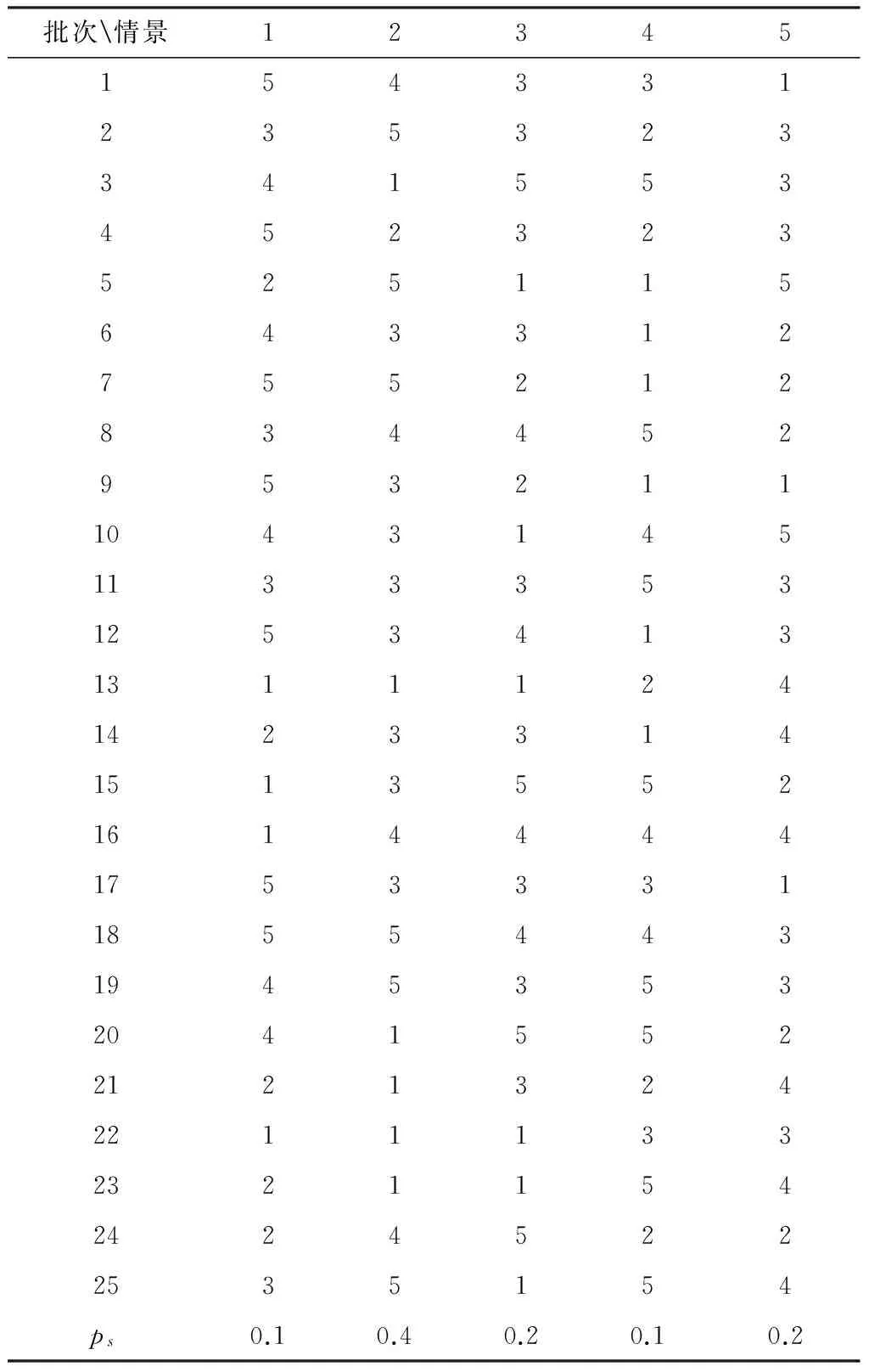
表1 各场景的产品组合和概率

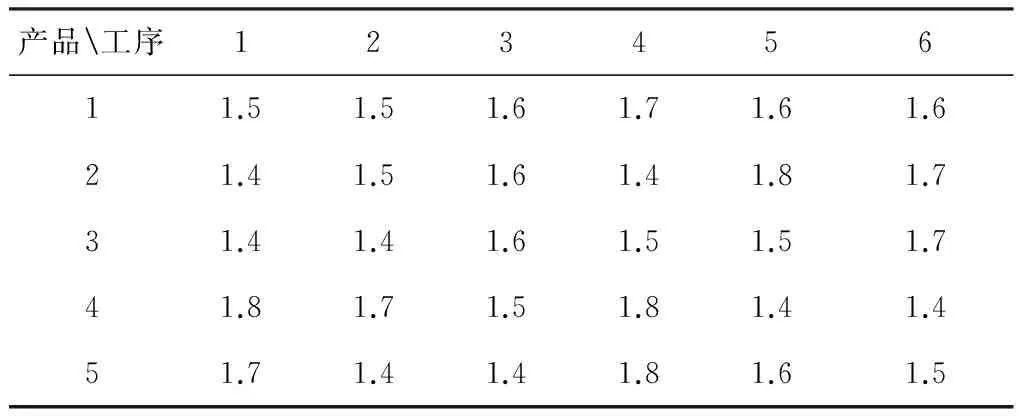
表2 产品在流水线上各工序的操作时间Tnl(min)

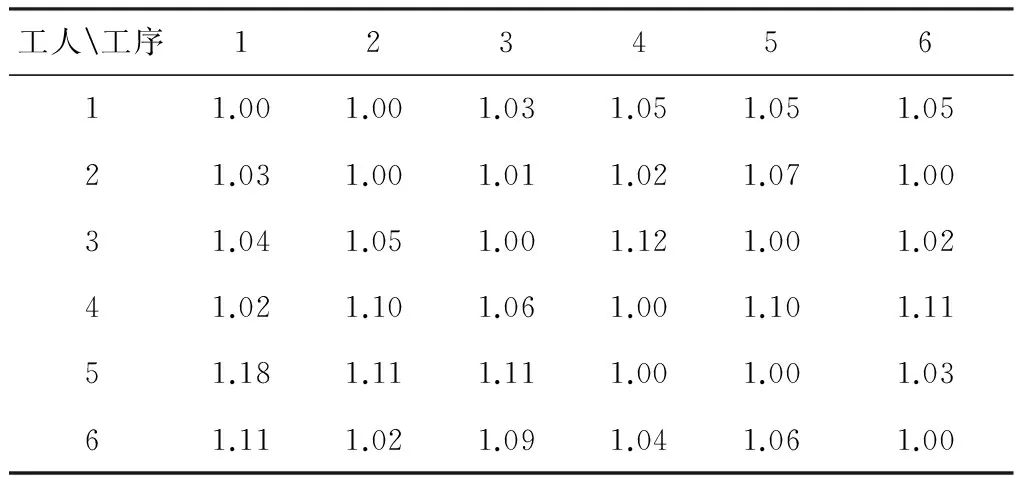
表3 工人对各工序的熟练程度γil

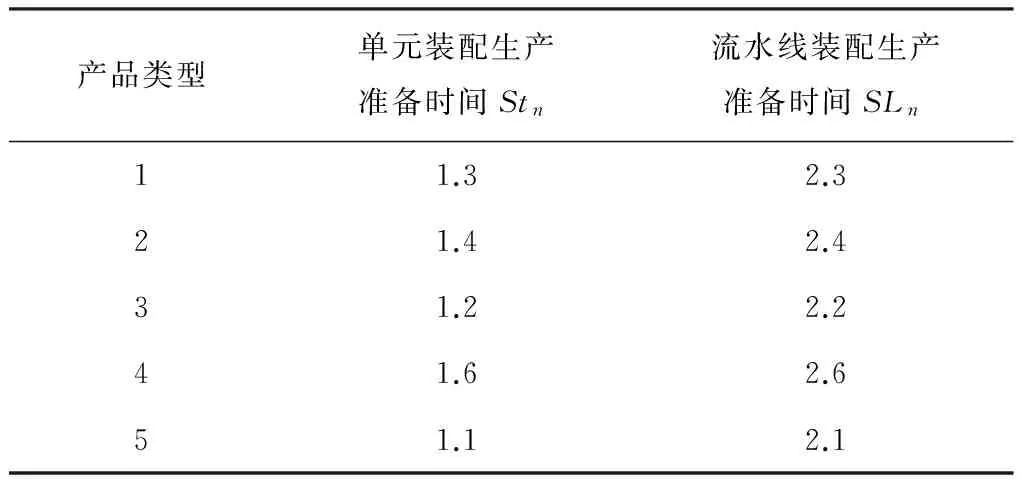
表4 产品生产准备时间(min)

4.2 基本算例的Pareto 解

运用本文提出的算法，种群规模为100，交叉概率为0.8，变异概率为0.2，迭代次数60次。求得由6名工人组成的流水线装配向单元装配系统的转化，考虑需求波动的因素所构建的单元系统有7个帕累托集，如表5和图3所示。运用NSGA-II算法求得的结果与枚举法求得的最优解相一致，证明算法的有效性。表中结果均为帕累托最优集并按照总加工周期的期望值从小到大排列，从表中计算结果可知，总加工周期的期望值较低时将同时具有较高的方差值，即期望值的更优是以波动性更大为代价的。决策者可以根据对总加工周期的偏好选择适合自己的方案进行单元系统的构建。若决策者更关注期望值的降低则选择方案一，若决策者更希望减少场景波动时的变动则选择方案五，即方差较小的方案。

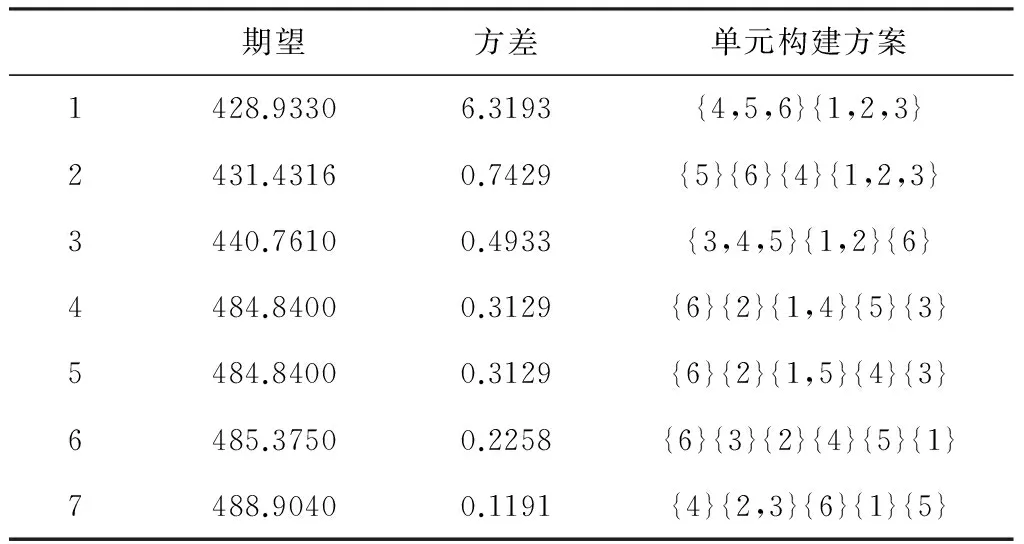
表5 由6名工人构成的流水线向单元转化的帕累托集

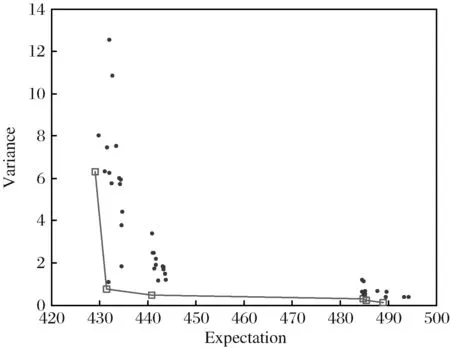
图3 由6人流水线向单元转化的帕累托集

当使用流水线装配方式进行生产时，总加工时间由节拍时间决定。根据流水线装配时间以及换产时间，在可能发生的五种场景下，流水线的总加工时间分别为687.3min；642min；709.7min；698.3min；654.5min，期望值为668.2min。对比运用日本式单元制造的方式，总加工时间的帕累托前沿中最大的期望值只有488.9min。这也证明了运用日本式单元装配系统进行该情境下的生产可以减少总加工时间、提升企业的生产效率。对于大规模算例采用多次运行算法的方式求得帕累托集，本实验对10人，15人和20人的日本式单元构建问题进行求解，由于篇幅有限不一一列举，10名工人流水线向单元转化构建方案帕累托集如图4和表6所示。

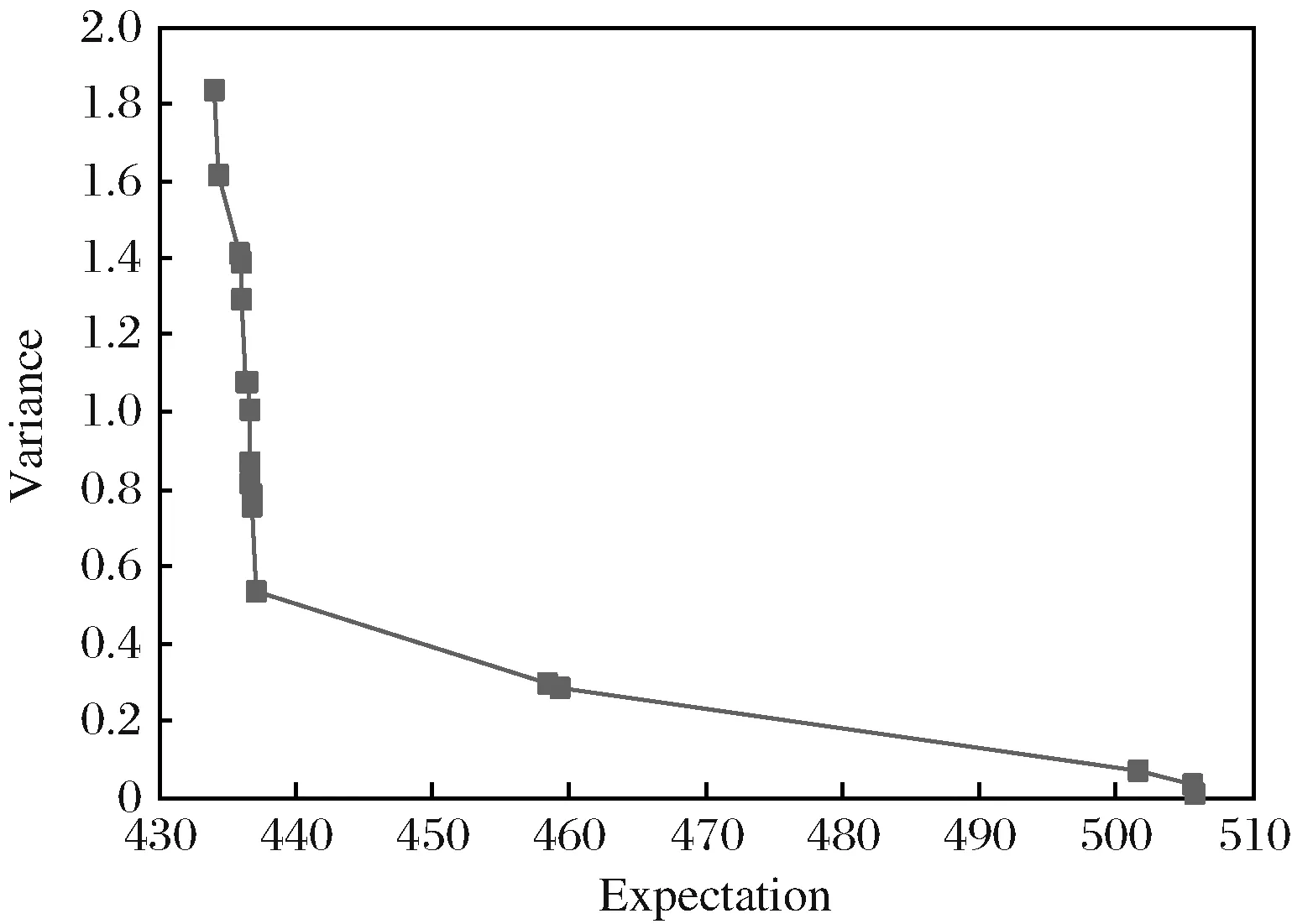
图4 10名工人流水线向单元转化结果的帕累托集

4.3 与任务已知型单元构建方法的比较分析

不考虑需求的波动，面对不同的需求场景时采用任务已知情境下的单元构建方法，构建的单元方案结果如表7所示。由结果可见，虽然在各场景下的最优方案获得了更短的加工时间，但是每种场景的最优情况构建方案中所构建的单元数量以及工人的分配组合各不相同。例如在构建生产系统时为了满足场景1的最优结果需要构建5个单元，而其他场景出现时因为所需单元的数量减少出现有单元空闲的情况，导致生产设备浪费的问题。与此同时，当需求波动时工人需要频繁转换工作所在的单元，且工作的伙伴也在变化。

为进一步分析在生产实践中各因素对构建方案的影响，在6名工人单元构建问题的基本实验基础上通过增加批次大小为5和2的实验，验证批次大小对单元构建方案的影响。实验结果如图4所示，在其他参数不变的条件下，随着批次大小的增加总加工周期的期望和方差均呈现减小的趋势，也就是说当批次大小增加时，单元系统的期望加工时间和稳定性得到提升。企业在进行生产调度的设计过程中，可以通过更改批次容量的方式提升生产系统的效率。

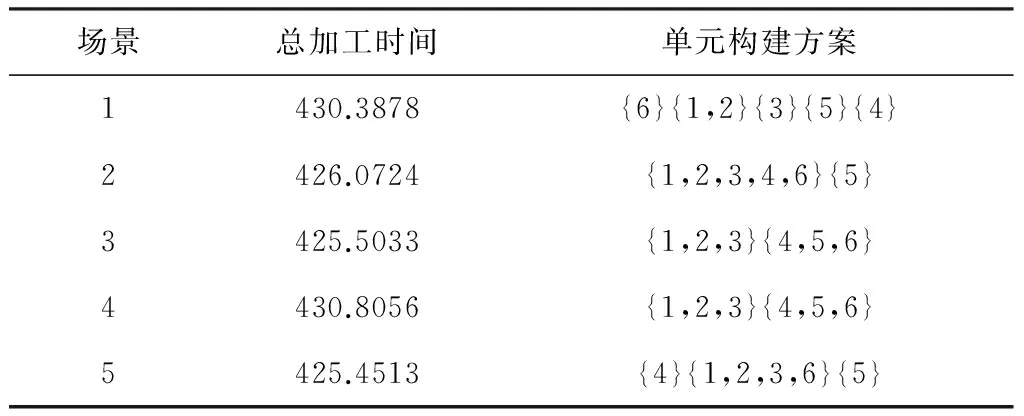
表7 各场景下的最优构建方案

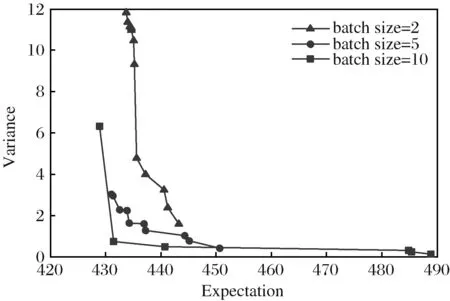
图5 批次大小对总加工周期的影响

5 结语

本文根据日本式单元制造问题的特点，研究需求波动情境下的流水线装配向单元装配的转换问题，以最小化总加工周期的期望和方差为目标函数，构建考虑需求波动的单元装配系统构建问题的多目标模型，决策构建的单元系统中单元的数量以及工人与单元对应关系的分配方案，以期通过构建稳定的单元装配系统应对波动的市场需求。根据问题的特征设计了针对大规模问题基于NSGA-II的启发式算法，并在小规模案例中与枚举法的结果对比验证了算法对模型求解的有效性。在大规模问题的求解问题中，采用了多次运行算法的方法进行求解，并得到较好的结果。通过对比任务确定型单元构建方法在应对需求波动环境时存在的不足分析本研究的重要性，并分析了生产批次大小对系统性能的影响。

参考文献：

[1] DTTL. 2016 Global Manufacturing Competitiveness Index[EB/OL]. [2016-8-1]. http://www2.deloitte.com/global/en/pages/manufacturing/articles/global-manufacturing-competitiveness-index.html.

[2] 徐辉, 侯建明. 需求不确定条件下的制造商订单分配模型[J]. 中国管理科学, 2016，24(3):80-88.

[3] 李稚, 谭德庆. 爱尔朗型按订单装配系统最优生产——库存控制策略研究[J]. 中国管理科学, 2016,24(6):61-69.

[4] 李群霞, 马风才, 张群. 供应链提前期供需联合优化库存模型研究[J]. 中国管理科学, 2015，23(4):117-122.

[5] 叶涛锋, 达庆利, 徐宣国. 需求与提前期不确定下的生产—销售协调[J]. 中国管理科学, 2016，24(10):133-140.

[6] 曹惺璧. 佳能细胞式生产方式[J]. 北大商业评论, 2010，(8):132-137.

[7] Yin Yong, Kaku I, Stecke K E. The evolution of seru production systems throughout canon[J]. Operations Management Education Review, 2008,(2):27-40.

[8] 刘晨光, 廉洁, 李文娟, 等. 日本式单元化生产——生产方式在日本的最新发展形态[J]. 管理评论, 2010,22(5):93-103.

[9] Stecke K E, Yin Yong, Kaku I, et al. Seru:The organizational extension of JIT for a super-talent factory[J]. International Journal of Strategic Decision Sciences, 2012,3(1):106-119.

[10] Villa A, Taurino T. From JIT to Seru, for a production as lean as possible[M]//AguilarMartin J J, YagueFabra J A. Procedia Engineering. AMSTERDAM: ELSEVIER SCIENCE BV, 2013:956-965.

[11] Isa K, Tsuyoshi T. Cell production and workplace innovation in Japan: toward a new model for Japanese manufacturing?[J]. Industrial Relations, 2002,41(4):548-578.

[12] Sakazume Y. Is Japanese cell manufacturing a new system?: a comparative study between Japanese cell manufacturing and cellular manufacturing[J]. Journal of Japan Industrial Management Association, 2005,55(6):341-349.

[13] Kaku I, Gong Jun, Tang Jiafu, et al. Modeling and numerical analysis of line-cell conversion problems[J]. International Journal of Production Research, 2009,47(8):2055-2078.

[14] Kaku I, Murase Y, Yin Yong. A study on human tasks related performances of converting conveyor assembly line to cellular manufacturing[J]. European Journal of Industrial Engineering, 2008,2(1):17-34.

[15] Liu Chenguang, Li Wenjuan, Lian Jie, et al. Reconfiguration of assembly systems: From conveyor assembly line to serus[J]. Journal of Manufacturing Systems, 2012,31(3):312-325.

[16] Liu Chenguang, Yang Na, Li Wenjuan, et al. Training and assignment of multi-skilled workers for implementing seru production systems[J]. The International Journal of Advanced Manufacturing Technology, 2013,69(5-8):937-959.

[17] Yu Yang, Gong Jun, Tang Jiafu, et al. How to carry out assembly line-cell conversion? A discussion based on factor analysis of system performance improvements[J]. International Journal of Production Research, 2012,50(18):5259-5280.

[18] Yu Yang, Tang Jiafu, Gong Jun, et al. Mathematical analysis and solutions for multi-objective line-cell conversion problem[J]. European Journal of Operational Research, 2014,236(2):774-786.

[19] Yu Yang, Tang Jiafu, Sun Wei, et al. Reducing worker(s) by converting assembly line into a pure cell system[J]. International Journal of Production Economics, 2013,145(2):799-806.

[20] Yu Yang, Tang Jiafu, Sun Wei, et al. Combining local search into non-dominated sorting for multi-objective line-cell conversion problem[J]. International Journal of Computer Integrated Manufacturing, 2013,4(26):316-326.

[21] 于洋, 唐加福, 宫俊. 通过生产线向单元转化而减人的多目标优化模型[J]. 东北大学学报(自然科学版), 2013,34(1):17-20.

[22] Srinivas N, Deb K. Muiltiobjectiveoptimization using nondominated sorting in genetic algorithms[M]. Cambridge, Massachusetts: MIT Press, 1994.

[23] Ali M, Siarry P, Pant M. An efficient differential evolution based algorithm for solving multi-objective optimization problems[J]. European Journal of Operational Research, 2012,217(2):404-416.

[24] Knowles J, Corne D. The Pareto archived evolution strategy: A new baseline algorithm for pareto multiobjective optimisation[C]//Evolutionary Computation, 1999. CEC 99. Proceedings of the 1999 Congress on, Washington, DC, USA, July 6-9, 1999.

[25] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002,6(2):182-197.

[26] Davis L. Applying adaptive algorithms to epistatic domains[C]//In Proceedings of International Joint Conference on Artificial Intelligence, Los Angeles, USA: 1985.