步进调频系统的测距精度分析

2018-05-08李建东赵文龙刘清成

空天防御 2018年2期

李建东，王蓉，赵文龙，胡杨，刘清成

(上海机电工程研究所，上海,201109)

0 引言

为获得对以F22为首的典型隐身飞机目标的最佳引战配合效果，通过对宽波束前向探测技术采用的步进调频算法进行研究，合理选择速度补偿参数，可以提高对目标测距分辨率，有利于识别目标闪烁能量中心和边缘部位、估算目标的能量中心和几何中心，为弹目遭遇姿态评估和最佳杀伤效果设计提供依据参数。

1 基于步进调频的一维距离像算法[1]

频率步进无线电引信通过发射一组载频跳变的脉冲串来获得大带宽，回波信号等同于目标的频域响应，只要发射的信号波形有足够的带宽，用常规的逆傅立叶变换处理就能孤立目标的强散射中心，从而实现距离高分辨率。频率步进体制因其实现比较简单、对信号处理的要求不太高等优点适宜在末制导系统中应用。频率步进体制雷达因其接收机瞬时带宽小、对数字信号处理硬件速度要求低等种种优点且波形设计灵活，已成为高距离分辨率雷达技术的发展趋势。

采用步进频信号能产生合成的运动目标距离像。假设包含N个脉冲的步进频脉冲串的脉冲重复频率(PRF)为fPRF，脉宽为τ，初始载频为f0，频率步进间隔为ΔF，则第k个脉冲的载频为步进频的发射信号为

fk=f0+(k-1)ΔF,k=1,2,…,N

(1)

(2)

假设目标静止不动，则距离R0处的目标回波信号为

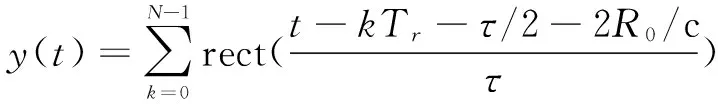
(3)

式中：c为无线电波传播速度。

与本振混频并滤波后，第k个脉冲回波的正交分量为

(4)

其复数形式为

S(k)=I(k)-jQ(k)=Akexp(-jΦk)

(5)

若目标以速度v远离雷达运动，则第k个脉冲的实际探测距离为

Rk=R0+(k-1)vTr

(6)

将式(1)和式(6)代入式(5)，得

[R0+(k-1)vTr])

(7)

目标的高分辨一维距离像可以通过对上式作离散傅里叶逆变换得到，即：

(8)

目标回波视频输出的相位表达式

(9)

将ψi分解为以下四项：

(10)

由于vt是常数，φ1也是常数，因此对合成距离像没有影响；φ2是正常的距离相位关系，包含了目标的距离信息，用来合成正确的目标距离像；φ3是目标速度引起的不同周期子脉冲间的相位变化；φ4是非线性频率变化和目标速度共同引起的不同周期子脉冲间的相位变化。φ3和φ4会破坏脉冲序列间正常的相位关系，导致目标一维距离像峰值的位置偏移和衰减。

若对由于目标运动引起的距离像失真进行补偿，则补偿项相位可表示为

(11)

2 频率步进引信系统的性能参数

频率步进引信系统主要性能参数包括系统距离分辨率、脉冲压缩比、脉冲宽度对应的原始距离分辨单元、最大不模糊距离窗、脉冲宽度与频率变化量的乘积、雷达系统总的相干处理时间、发散因子和时移因子等[2]。

根据某采用高重频脉冲步进频测距体制的引信系统任务指标要求，对引信系统工作参数初步设计如下。

2.1 发射信号带宽

频率步进脉冲串波形是一种量化了的线性调频波形，它通过载频增量在脉冲到脉冲之间的递增，获得大等效调频带宽。当确定系统距离分辨率后，再据此确定波形等效调频带宽。引信测距精度指标要求优于1 m，因此引信系统距离分辨率也必须处于同等水平，故选取发射信号带宽为250 MHz，该带宽下距离分辨率为

(12)

2.2 发射脉冲宽度

发射脉冲宽度决定系统的盲区和作用距离，本项目选取发射脉冲宽度30 ns。

2.3 步进频测距脉冲重频

在近距工作模式下，为降低系统复杂度，步进频测距脉冲重频设计首先要保证测距范围内无模糊工作，其不模糊工作下的重频应小于1.6 MHz。

选取步进频测距脉冲重频暂定为1 MHz，即：脉冲重频Tr=1 μs，对应的脉冲无模糊测距的最大距离150 m。

2.4 步进频发射信号波形设计

对于运动目标来说，通常需要考虑系统总相干处理时间，即脉冲个数N与脉冲重复周期Tr的乘积。如果在系统总相干处理时间内目标离开了天线主波束，回波信息将丢失，因此为了有效地获得一串目标回波，系统总相干处理时间必须小于目标在波束内的驻留时间。这样频率步进雷达波形中脉冲个数的选择需要考虑天线波束宽度以及波束扫描频率等因素的影响。同时，考虑大作用距离下尽量提高信号积累时间以提高系统灵敏度，故步进频调制数N取值应尽可能增大，考虑信号处理时间余量。

本项目步进频调制数N取256，且选用步进频正频率调制方式进行目标距离的测量。一次步进频测距周期内发射信号波形参数如下：发射脉宽τ为30 ns，脉冲重复周期Tr为1 μs，步进数N为256，发射信号带宽250 MHz，单次步进频率Δf为976.6 KHz，τ·Δf<1，满足步进频测距紧约束条件。

3 多普勒耦合修正对引信系统测距精度的仿真分析

根据前述机理分析，为确保步进频测距引信系统测距精度，需要对目标运动引起的距离像失真进行补偿。本项目中根据主动GIF导引头实时测量的弹目接近速度计算获得多普勒耦合修正因子，因此导引头系统速度测量速误差会影响前向引信系统距离测量精度。此外，由于弹目交会段时间极短，通常假设弹道与目标间做匀速直线运动，多普勒耦合修正采用固定速度值进行修正，而实际弹目接近速度在弹目交会过程中是变化的，也存在一定的补偿误差。

根据多普勒耦合效应的数学公式对测速误差影响测距精度情况进行仿真分析，参数设置为R=50 m，f0=35 GHz，v=3 000 m/s，Tr=1 μs，Δf=976.6 KHz，τ=30 ns，仿真结果如图1所示。

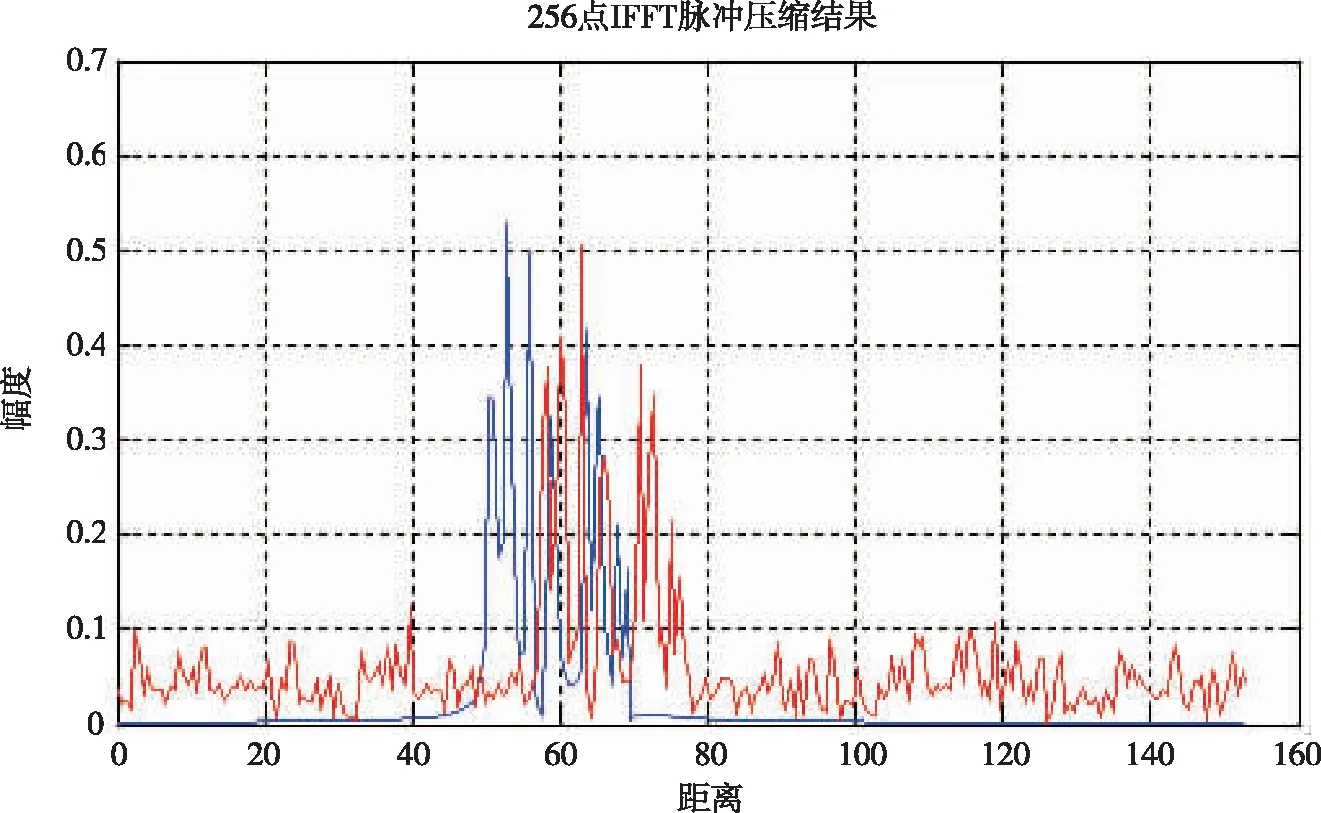
图1 目标距离50 m时测速误差200 m/s回波(红色)及无测速误差回波(蓝色)示意图Fig.1 The contrast of echo (red) with velocity-measurement error (200 m/s)and echo (blue) of no velocity-measurement error (0 m/s) when target distance is 50 m

当IFFT点数为M时，静止目标成像在l0=R/Δr=2NΔfR/c，距离分辨率Δrs=c/(2MΔf)；目标径向运动时距离的偏移因子L=(M/N)·(vNTr/Δr)·(f0/B)=2f0MvrTr/c，实际成像距离为Rvr=(l0-L)Δrs，因此由相对运动引起的偏移距离为ΔR=R-Rvr=(1-N/M)·R+f0vrTr/Δf，当不增加IFFT变换点数时，则由相对运动引起的偏移距离为ΔR=f0vrTr/Δf。

根据上述分析，采用相对速度进行多普勒耦合修正补偿后实际的偏移距离主要由测速误差或者补偿误差引起的，针对本系统测速误差与偏移距离的仿真结果如表1所示。

表1 步进调频测速误差与偏移距离的关系表

续表1

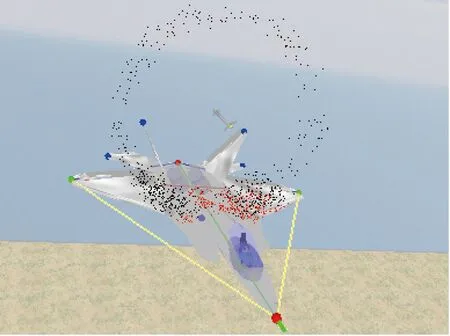
图2 基于一维距离像的引战配合仿真图Fig.2 The simulation figure of fuze-warhead coordination based on range profiles

仿真结果显示测速误差为28 m/s，目标距离偏移1.003 5 m，基本与系统小于1 m的测距精度指标相当。即:系统要满足测距精度指标，则导引头测速误差应不大于28 m/s。图2为测速误差为28 m/s时，基于一维距离像的命中点识别的引战配合效果图，可见在该测距精度条件下战斗部破片飞散区能够很好覆盖设计的命中区。