“平衡”里面学问多——小学跨学科兴趣活动探讨

◆吴云

在教学《怎样使杠杆保持平衡》（冀教版科学五年级下册第6页）之后，学生意犹未尽。一位学生说：“我的直觉是，一边挂得重，和中间靠得近，另一边挂得轻，必须离中间远一些才能把这头拉下来，达到平衡。”细细品味，这与数学的反比例，以及美术的构图均衡不是殊途同归吗?的确，六年级下册数学《反比例》（人教版第47-48页）、三年级下册美术《平平稳稳》（第6-7页）都与“平衡”这一主题有关。能否组织一次兴趣活动，把它们有机结合起来呢？

新版《小学科学课程标准》特别提到：“倡导跨学科学习方式。科学（science）技术(technology)工程(engine)与数学(math)即STEM是一种以项目学习问题解决为导向的课程组织方式。它将科学、技术、工程、数学有机地融为一体，有利于学生创新能力的培养。科学教师可以尝试运用于自己的教学实践。”在实际教学中，找准某一个主题，组织开展学生喜爱的、高效的跨学科整合式兴趣活动，能够有效促进学生核心素养的提升。

有了新课标的支撑，我设计了一堂融科学、数学、美术于一体的跨学科整合式兴趣活动课。活动简要流程、优势分析及实施建议如下：

一、活动简要流程

（一）复习杠杆平衡，沟通数学反比例

1.自由猜想

如图表1，思考：在杠杆的右边的某一格处，挂几个钩码可以平衡？

图表1右边挂几个才平衡

2.动手验证

3.汇报整理

共4种挂法：第一格挂6个，第二格挂3个，第三格挂2个，第六格挂1个。

其中第二格挂3个是左右对称的，无数学分析的价值。其余挂法对应的算式如下：

表格1不同挂法对应的算式

4.数据分析

对比表格1中右边的三个算式。领悟数学的积不变规律和“反比例”关系。

5.尝试运用

如图表2，根据反比例关系，能写出哪些乘法算式？请挂上挂钩码试试。

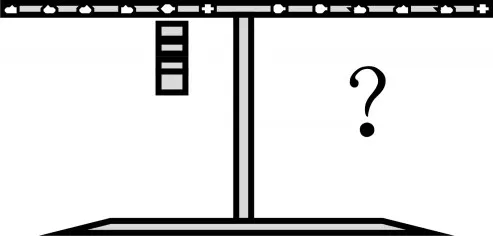
图表2尝试运用

由1×8=8,4×2=8,8×1=8三个算式在相应的位置挂上合适的钩码，实际验证。

6.自主练习

自己挂钩码。运用反比例知识先计算一下在什么位置，挂几个钩码。如果一种挂法都找不出来，也要用数学知识说明理由。

（二）直觉杠杆平衡，沟通美术构图均衡

1.不用计算，你能一眼看出下面杠杆的哪一边重吗？说说为什么。

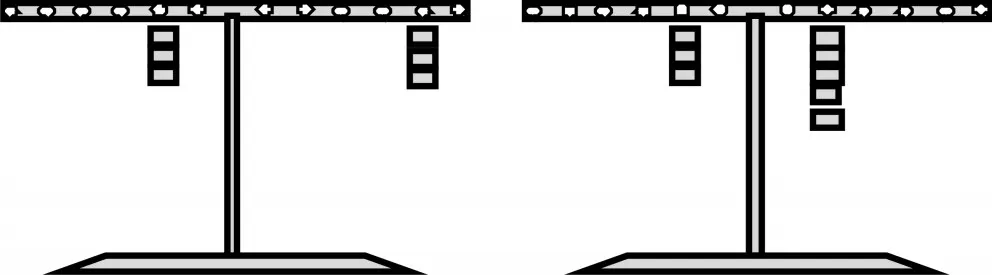
图表3感觉哪边重？

2.看看以下两幅画面，每幅图在平衡上有什么感觉？

图表4每幅图在平衡上有什么感觉？

虽然没有杠杆，没有支点。但我们仍然能感觉到这两幅图都是左边偏重，右边偏轻。这在美术上称为不均衡。均衡的原理，就是根据人的视觉形象，产生重量感的心理反应而发展起来的。可以想象为杠杆的平衡。

在上面两幅图中，可以加上一些图形，让他们不再左重右轻。你能做到吗？

展示学生作品。如：

图表5弥补后的图形举例

3.欣赏图表6。最高的楼房为什么不摆在图片正中间?

图表6楼房图片

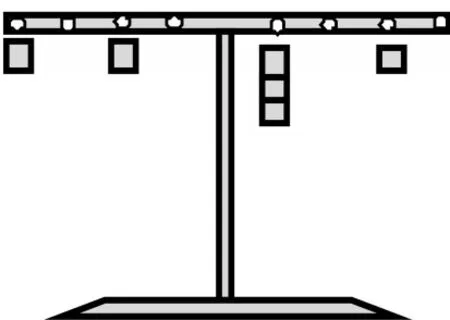
图表7楼房图片的杠杆示意图

（三）回归杠杆原理，沟通学科联系

1.根据上图，画出其杠杆示意图（见图表7）

2.用算式证明楼房图左右均衡的原因

4×1+2×1=1×3+3×1

（四）用自己的话说说杠杆与美术构图均衡、数学知识之间的联系

二、活动优势分析

这堂跨学科整合式兴趣活动课，把五年级科学“怎样使杠杆保持平衡”、六年级数学中“反比例”、三年级美术“平平稳稳”整合起来，各学科知识统摄于“平衡”这一主题，展现其逻辑美、形象美。在有限的活动时间内，学生的认知能力、思维能力得到最有效的培养，显示了跨学科知识整合的鲜活生命力。跨学科整合式兴趣活动的优势有：

（一）有利于提高教学的时间效益

在短短的一节活动课内，把与平衡有关的科学、数学、美术知识融合在一起，一举三得。从时间上看，是非常有效的。试想，如果不打破学科界限，各学科教师在活动中分别进行训练，势必各自为政，必须为本学科的教学做必要的准备，必须分别实施必要的练习，必须分别提炼各自的总结。这样，就会浪费不少组织教学活动的时间，训练也很容易在一些环节上无效重复，时间效益大打折扣。

（二）有利于对某一主题的透彻理解

“1+1＞2”。把科学、数学、美术有关平衡的知识点融为一体，就对“平衡”有了直观的、多角度的、精确的、艺术的理解，由表及里，深入透彻。比如，数学上，我们对反比例的理解仅限于计算的吻合，但有了杠杆这一活生生的实物，真真切切地摆在这里，或平或斜，一目了然，这就向呆板的数学计算注入了强大的活力，学生兴趣陡增，练习成效自然大大提高。在美术构图的均衡的探究中，学生意识到均衡的美实际上来源于杠杆原理，是我们必须遵循的自然法则之一。这就对学生进行了很好的启蒙，万事追根溯源，奥秘就在其中。

（三）有利于发展学生的创新思维

约翰·波拉克认为：创新的本能，是类比思维的力量。创新不是凭空想象,而是由此及彼。创新思维是创新力的核心,而发散思维是创新思维的核心。它内在地包含了逆向思维、横向思维、求异思维等其它思维方式，同时它也是想象、联想、灵感等思维的前提和基础。利用杠杆的平衡条件，联想到数学反比例的规律，联想到美学的均衡，都是发散思维的表现，是培养学生创新能力的良好契机。养成了类比推理的思维习惯，并进行大胆推测和验证，很多困扰发展的问题都可以得到解决。例如，惠更斯提出的光的波动说，就是类比声的波动而发现的；欧姆将其对电的研究和傅立叶关于热的研究加以类比，建立了欧姆定律。鲁班发明锯子，也是类比推理的杰作。

三、活动实施建议

跨学科兴趣活动不是漫无目标的大杂烩玩耍课，必须精心选材，合理把握时机，才能达到最佳活动效果。

（一）要善于发现各科知识内在的相关性

例如，语文课文《五彩池》（人教版四年级上册第162-163页），对“五彩”的成因进行了简要的分析：“石笋表面凝结着一层细腻的透明的石粉。阳光透过池水射到池底，石笋就像高低不平的折光镜，把阳光折射成各种不同的色彩。”正巧，科学教材《七色光》（冀教版三年级下册第30页）就是探究光的折射现象。那么，透明石粉是如何发挥作用的？与彩虹现象中的什么物体类似？教师需认真研究之后才能进行有效整合。只有不断加强教师自身综合素养的提高，善于发现各科知识内在的相关性，才有可能游刃有余地发掘利与整合的知识点，让学生将知识融会贯通，得到最优化发展。

（二）要正确区分各学科相关知识的相似程度

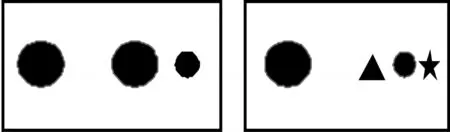
为有效培养学生发散思维，必须为学生呈现有较强相似性的学习材料。迁移较远，跨度较大的学习材料很容易干扰本次活动主题。例如，美术构图的均衡，不仅体现在物体大小、布局上，在色彩，明暗等方面也能体现出来。比如下图：

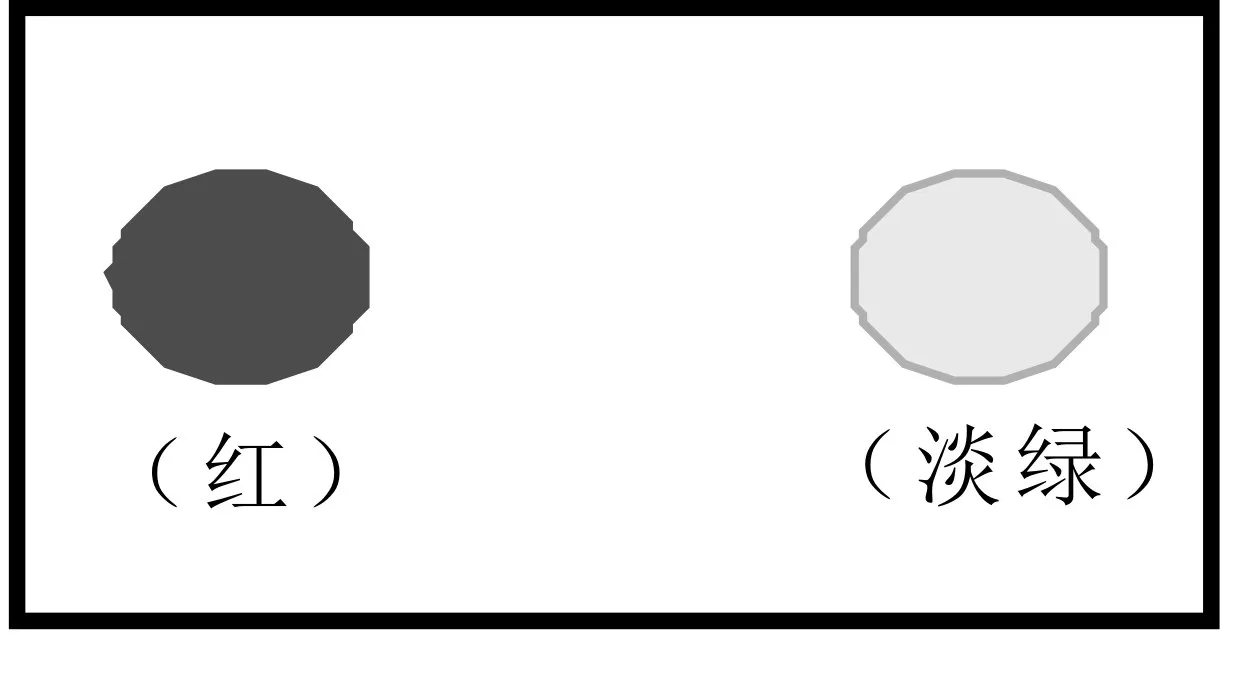
图表8不同色彩对构图均衡的影响

左边一个红色的圆，右边一个淡绿色的圆，它们尽管处于图片左右对称的位置，大小相等，但感觉不平衡。这是色彩的均衡问题。而我们在开展“杠杆平衡”这一主题活动中，重点理解的是由物体大小、位置而产生的的重量感。但在这里，颜色、浓淡等与科学上杠杆的钩码重量上的平衡已经有了较大迁移，需要美术课的进一步学习，借助更加深刻的原理才能进行准确理解。所以，对于相似性不强的知识点，暂不加入，以免影响当前的基本理解。

（三）要准确把握各学科相关知识的难易程度

比如人教版小学二年级数学教材中，《表内乘法二》（第72-87页）已经完成乘法口诀的教学。如果利用杠杆的平衡，引导学生对乘法口诀进行应用，提高学生乘法口诀的熟练程度，也是很有创意的。但是，小学科学教材中，杠杆的教学放在五年级，二年级学生要运用杠杆帮助学习乘法口诀的话，就必须花大量时间对杠杆本身进行熟悉，这就增加了学习的时间成本，也不太符合低年级儿童的年龄特点。因此，利用杠杆对二年级学生进行乘法口诀的训练偏难，不适合开展这一整合式兴趣活动。

再如科学课《怎样使杠杆保持平衡》出现在五年级下册。小学数学《反比例》是六年级下期的知识。但数学方面，五年级的学生已经对积不变规律有了清楚的理解，在知识准备上已经具备探究反比例的条件，因此完全可以在玩中感悟“反比例”这一数学知识。

跨学科整合式兴趣活动是学校课程改革的有益尝试之一。在日常教学活动中，只要教师注重学生的全面发展，注重学生核心素养的提升，多留心于利于整合的知识点，就可以整合出优质高效的跨学科兴趣活动，为课程改革的进展做出实实在在的努力，为学生的终身发展奠定坚实的基础。