基于界栅的日地平动点编队飞行碰撞规避控制研究
2018-05-07张科何振琦吕梅柏王靖宇
张科, 何振琦, 吕梅柏, 王靖宇
(1.西北工业大学 航天学院, 陕西 西安 710072; 2.航天飞行动力学技术重点实验室, 陕西 西安 710072)
航天器编队飞行的研究工作从20世纪90年代末开始就没有间断过,特别是近些年随着小卫星技术的发展,成为了研究热点。目前国际上已经有不少的空间科学实验任务采用航天器编队飞行来实现,比较典型的有美国NASA的A-Train计划、MMS计划[1-2]等。
航天器编队飞行技术的一大特点是多颗小航天器在空间组成特定的构形协同工作,密切联系,以分布方式构成一颗大的“虚拟航天器”(或称为“分布式卫星系统”)[3-5],从而产生系统理论中的“涌现”现象[3-5],在性能上超越单颗航天器系统。
在编队飞行中,由于各种摄动的影响,将会使编队构型产生漂移,而且由于各种硬件、软件故障的问题,都会增加编队飞行过程中航天器碰撞概率。如何避免编队航天器之间的碰撞成为卫星编队飞行设计中必须考虑的重要问题。本文通过微分对策中的界栅理论[4]把相邻2个飞行器的最小距离作为约束集,建立Hamilton函数并得到最优控制律[6-8],构造界栅理论及相应界栅轨迹,划分碰撞区与非碰撞区[6-8],从而实现编队航天器防碰策略设计研究。
1 建立微分对策系统状态方程
假设仅考虑2颗卫星在同一平面内相对运动,即目标星为E,追赶星为P,则多颗卫星以此类推。图1为编队飞行追逃关系模型示意图。

图1 飞行器编队飞行追逃关系模型示意图
(1)
式中,μ1为太阳开普勒常数,μ2为地月系开普勒常数,rp1是由太阳质心指向航天器P的矢量,rp2是由地月系质心指向航天器P的矢量,re1是由太阳质心指向航天器E的矢量,re2是由地月系质心指向航天器E的矢量。F为航天器轨控发动机推力,u和v分别为推力Fp和Fe与X轴的夹角,Mp与Me分别为航天器P与航天器E的质量。
2 最优控制量的求解及界栅的构造
假设航天器P域与航天器E在同一平面内组成追逃模型,星间临界碰撞距离为l,则对策目标约束集D为圆域[9]:
(Xe-Xp)2+(Ye-Yp)2-l2≤0
(2)
当编队航天器间相对距离大于l,则不会发生碰撞,反之则发生碰撞。
根据微分对策理论,Hamilton函数可表示如下:
H(Xp,Xe,Yp,Ye,u,v,γ)=γ1Vxp+γ2Vyp+
γ3-μ1‖rp1‖3+μ2‖rp2‖3Xp+FpMpcosv+
γ4-μ1‖rp1‖3+μ2‖rp2‖3Yp+FpMpsinv+
γ5Vxe+γ6Vye+
γ7-μ1‖re1‖3+μ2‖re2‖3Xe+FeMecosu+
γ8-μ1‖re1‖3+μ2‖re2‖3Ye+FeMesinu=
Hp+He+H0
(3)
式中:γ=[γ1γ2γ3γ4γ5γ6γ7γ8]T∈R8是任意向量;且
Hp(v)=γ3FpMpcosv+γ4FpMpsinv
He(u)=γ7FeMecosu+γ8FeMesinu
H0=γ1Vxp+γ2Vyp-γ3μ1‖rp1‖3+μ2‖rp2‖3Xp-
γ4μ1‖rp1‖3+μ2‖rp2‖3Yp+γ5Vxe+γ6Vye-
γ7μ1‖re1‖3+μ2‖re2‖3Xe-
γ8μ1‖re1‖3+μ2‖re2‖3Ye
因此:
maxuminvH(Xp,Xe,Yp,Ye,u,v,γ)=
minvHp(v)+maxuHe(u)+H0
(4)
令dHp(v)dv=0,即
FpMp(-γ3sinv+γ4cosv)=0
(5)
解得
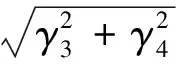

显然有
d2Hp(v*)dv2=-(γ3sinv*+γ4cosv*)>0
(7)
由(6)式、(7)式确定v*是航天器P的最优策略。类似可求得航天器E的最优策略u*,其满足


于是,可得
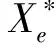

将目标集
∂D={(Xp,Xe,Yp,Ye)|(Xe-Xp)2+
(Ye-Yp)2-l2=0}
写成参数形式:
Xp()=φ1(s)=s1,Yp()=φ2(s)=s2,
Vxp()=φ3(s)=s3,Vyp()=φ4(s)=s4,
Xe()=φ5(s)=s1+lcoss5,
Ye()=φ6(s)=s2+lcoss5,
Vre()=φ7(s)=s3,Vθp()=φ8(s)=s4
式中,s=(s1,s2,s3,s4)T;s5为与x轴正方向的夹角,-π≤s5≤π;为捕获时间。
由界栅构造理论:
∑mi=1γi∂φi(s1,s2,…,sm-2)∂sj=0
γT·γ|∂D=1,(j=1,2,…,m-2)
(10)
由方程组(10)中第一个式子可得:
γ1()+γ5()=0
γ2()+γ6()=0
γ3()+γ7()=0
γ4()+γ8()=0
-γ5()lcoss5+γ6()lcoss5=0
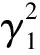
(11)
再结合方程组(10)中第二个式子可得∂D上的单位法线向量为
γ|∂D=(coss58,sins58,coss58,
sins58,-coss58,-sins58,-coss58,-sins58)T
显然Hamilton函数可写成:
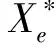
18Qsin(s5+a)-FpMp+FeMe
(12)
式中:
Q={[Vxp-Vxe+(μ1‖re1‖3+μ2‖re2‖3)Xe-(μ1‖rp1‖3+μ2‖rp2‖3)Xp]2+
[Vyp-Vye+(μ1‖re1‖3+μ2‖re2‖3)Ye-(μ1‖rp1‖3+μ2‖rp2‖3)Yp]2}12
a=arctanVxp-Vxe+(μ1‖re1‖3+μ2‖re2‖3)Xe-(μ1‖rp1‖3+μ2‖rp2‖3)XpVyp-Vye+(μ1‖re1‖3+μ2‖re2‖3)Ye-(μ1‖rp1‖3+μ2‖rp2‖3)Yp
以下有3种情况:
1) 当sin(s5+a)>FpMp+FeMe/Q时,则整个目标边界集∂D是NUP,不存在界栅,航天器P与航天器E总可以发生碰撞,整个对策空间都是碰撞区。
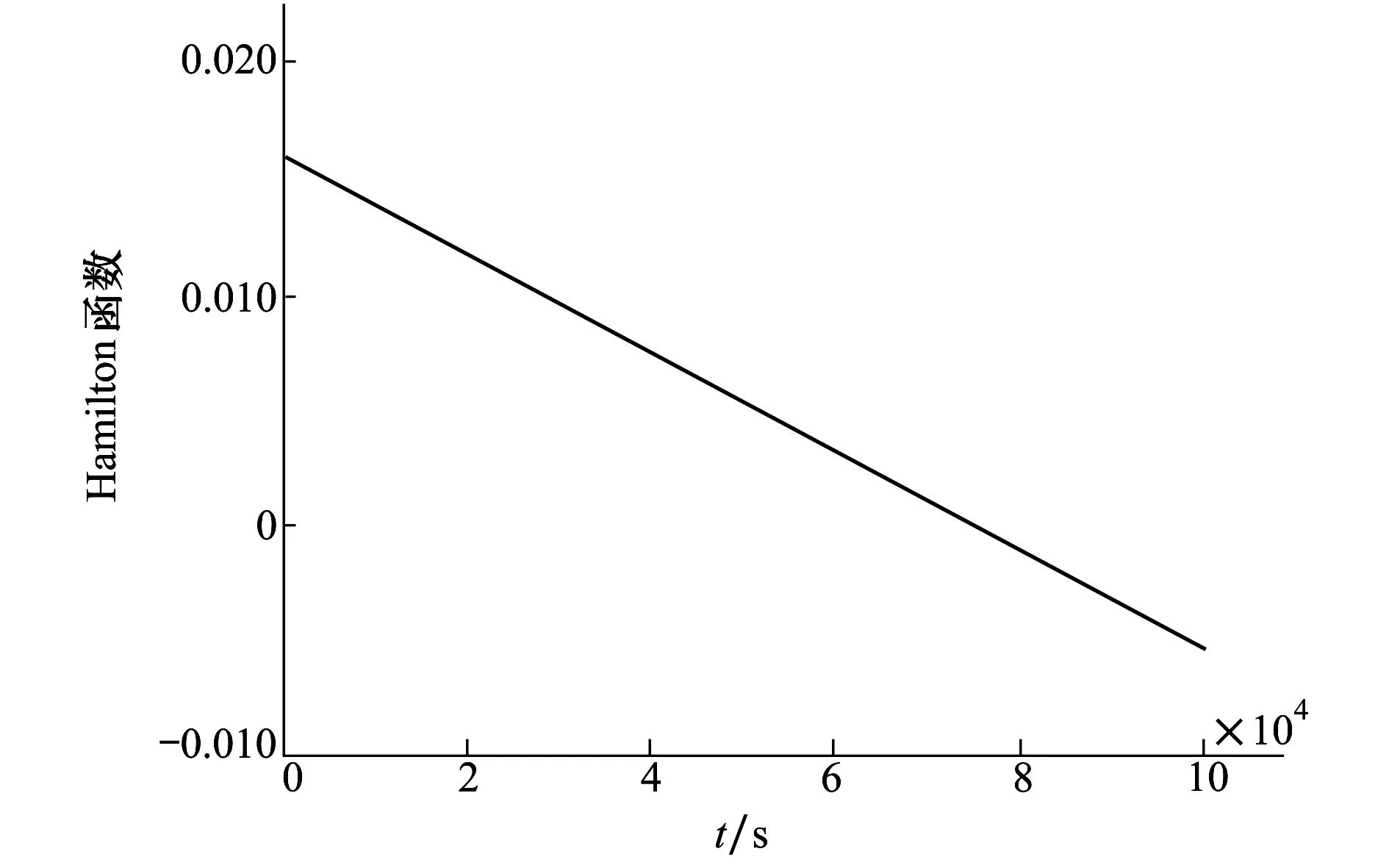
2) 当sin(s5+a) 3) 当sin(s5+a)=FpMp+FeMe/Q时,则整个目标边界集∂D是BUP,在这种情况下,一定存在界栅B。下面以对应于BUP上任意一点s为初始点倒向构造界栅B。 易于得到倒向协态方程组为: dγ1dτ=μ1‖rp1‖3+μ2‖rp2‖3coss5- (coss5Xp+sinYp)μ1‖rp1‖92+μ2‖rp2‖92Xp dγ2dτ=μ1‖rp1‖3+μ2‖rp2‖3sins5- (coss5Xp+sinYp)μ1‖rp1‖92+μ2‖rp2‖92Yp dγ3dτ=-coss5 dγ4dτ=-sins5 dγ5dτ=-μ1‖rp1‖3+μ2‖rp2‖3coss5- (coss5Xe+sinYe)μ1‖rp1‖92+μ2‖rp2‖92Xe dγ6dτ=-μ1‖rp1‖3+μ2‖rp2‖3sins5- (coss5Xe+sinYe)μ1‖rp1‖92+μ2‖rp2‖92Ye dγ7dτ=coss5 dγ8dτ=sins5 (13) 相应的初始条件为: γ1(0)=12coss5,γ2(0)=12sins5, γ3(0)=12coss5,γ4(0)=12sins5, γ5(0)=-12coss5,γ6(0)=-12sins5, γ7(0)=-12coss5,γ8(0)=-12sins5 式中,τ=-t0,倒向状态微分方程组为: (14) 以及倒向初值条件为: 简单的积分可得: 则所求的界栅B为: (17) 即为一个圆,界栅B把对策空间R2分为2个部分,由B围成的圆域(包括B本身)为捕获区,圆域之外的区域为躲避区。 文本仿真实例的初始条件如下: 假设航天器P与航天器E的质量及大小相同,质量均为2 000 kg;航天器P处于幅值为900 000 km的运行轨道上,捕获半径为5 km,以日地平动点L2点附近编队飞行为例,具体的L2点基本常数[10]如表1所示: 表1 日地系统L2点基本常数 航天器P与航天器E在坐标系下的位置与速度[11-12]分别为: Xp(0)=87 028.508 409 km Xe(0)=87 028.618 409 km Yp(0)=-24 739.512 629 km Ye(0)=-23 268.613 245 km Vxp=8.995 877 m/s Vyp=121.605 675 m/s Vxe=8.285 877 m/s Vye=120.924 877 m/s 由于编队飞行时,航天器间距较近,可忽略轨道引力,太阳光压等摄动力影响。对Hamilton函数进行Matlab仿真如图2所示: 图2 Hamilton函数随时间变化曲线 在图2中,可以看到Hamilton函数存在大于0、等于0、小于0的情况,也就是航天器间存在非碰撞区、界栅和碰撞区。 对方程(4)做积分dHpdFp=0可得最优控制推力表达式: γ3Mpcosv+γ4Mpsinv (18) 再将(13)式代入(18)式可得: sins58Mpcosv-coss58Mpsinv= -18Mpcos(s5+v) (19) 经过matlab仿真可得航天器P的控制力Fp随倒向时间变化如图3所示: 图3 航天器P的控制力Fp随倒向时间变化曲线 在图3中,首先,控制力Fp随倒向时间的变化呈先由小变大再由大变小的循环过程,中间有反向的出现,这是由于航天器P在追逃过程中,两航天器的位置发生了改变造成控制力方向的改变。 编队飞行技术是深空探测方向的一个重要研究方向,本文将任意2个航天器间的最小距离作为临界距离,运用微分对策中的界栅理论将整个对策空间分为碰撞区与非碰撞区,碰撞区与非碰撞区的重叠部分即为界栅。通过对界栅区域的构造,能够保证航天器间不发生碰撞。经过实例仿真证明该方法简单可行。 参考文献: [1] Lian Yijun, Gerard Gómez, Josep J Masdemont, et al. Station Keeping of Real Earth-Moon Libration Point Orbits Using Discrete-Time Sliding Mode Control[J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(10): 3792-3807 [2] Josep Virgili Llop. Autonomous Optical Navigation for Orbits around Earth-Moon Collinear Libration Points[J]. Acta Astronautica, 2013, 86(5/6): 119-125 [3] 徐明. 平动点轨道的动力学与控制研究综述[J]. 宇航学报, 2009, 30(4): 1299-1313 Xu Ming. Overview of Orbital Dynamics and Control for Libration Point Orbits[J]. Chinese Journal of Astronautics, 2009, 30(4): 1299-1313 (in Chinese) [4] Daren Lee, Krishna Dev Kumar, Manoranjan Sinha, et al. Fault Detection and Recovery of Spacecraft Formation Flying Using Nonlinear Observer and Reconfigurable Controller[J]. Acta Astronautica, 2014, 97(4/5): 58-72 [5] Lü Jing, Li Junfeng, Lu Qishao, et al. Periodic Orbits Based on Geometric Structure of Center Manifold around Lagrange Points[J]. Astrophys Space, 2012, 340:17-25 [6] 李登峰. 微分对策及其应用[M]. 北京: 国防工业出版社, 2000 Li Dengfeng. Differential Games and Applications [M]. Beijing, National Defense Industry Press, 2000 (in Chinese) [7] Lin W. Distributed UAV Formation Control Using Differential Game Approach[J]. Aerospace Science and Technology, 2014, 35(3): 54-62 [8] Andrea L′fflitto. Differential Games, Partial-State Stabilization, and Model Reference Adaptive Control[J]. Journal of the Franklin Institute, 2017, 354(1): 456-478 [9] 张秋华, 孙毅, 黄明明, 等. 近地共面轨道上两飞行器在径向连续小推力下的追逃界栅[J]. 控制与决策, 2007, 22(5): 530-534 Zhang Qiuhua, Sun Yi, Huang Mingming, et al. Pursuit-Evasion Barrier of Two Spacecrafts under Minute Continuous Radial Thrust in Coplanar Orbit[J]. Control and Decision, 2007, 22(5): 530-534 (in Chinese) [10] 熊攀. 日地L2平动点编队飞行高精度位置保持建模及控制[D]. 哈尔滨: 哈尔滨工业大学, 2011 Xiong Pan. Modeling and Control of High Precision Postion Keeping for the Sun Earth L2 Point Formation Flying[D]. Harbin, Harbin Institute of Technology, 2011 (in Chinese) [11] Korobtsev Iv, Goryashin Ve, Eselevich Mv. Results of Tracking a Spacecraft in the Vicinity of the L2 Libration Point of the Sun-Earth System[J]. Journal of the Franklin Institute, 2017, 61(2): 153-159 [12] He Zhenqi, Zhang Ke, Lü Meibai. Research on Control Method of Keeping Flight Formation by Using SDRE on the Sun-Earth Libration Points[J]. Advances in AstronomAdvances in Astronom, 2017, 1(1): 5-16




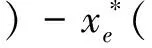
3 实例仿真与分析


4 结 论
