钻杆供电直流电法超前探测快速反演

刘 磊

(中煤科工集团西安研究院有限公司，西安 710077)

0 引言

直流电法超前探测是解决煤层巷道掌子面前方探测的一种常用方法[1-3]。传统方式在迎头前方布置三个供电电极，供电电极之后以一定间距布置若干个接收电极，供电电极分别供电，得到三条电位差曲线并计算相应视电阻率曲线。通过“交汇”方法进行迎头前方电阻率分布一维解释[4-5]。数值模拟结果表明，迎头采用点电极供电方式对前方激励有限，巷道内可测量异常幅度较小[6]。“交汇”处理方法过程相对简单，运用较多。由测量数据到电性分布属于地球物理反问题，求解反问题需要建立待反演物理量变化梯度与测量数据之间的近似线性关系，即计算雅克比矩阵，不断获取模型修正量，通过反复迭代最终获得反演结果。对于直流电法反演的研究一般集中于地面情况，从最初的一维到目前的三维反演都有文献论述[7-8]。

直流电法反演研究文献很多，shima H在1987年提出了地面电阻率成像的概念，将待成像区域网格化，试图建立单元电阻率与视电阻率的近似线性关系，后来又尝试将电位表示成级数和，但对于高阻体和电导率急剧变化的模型遇到了困难[9-10]。毛先进利用格林函数导出2.5维问题中研究区域电位满足的边界方程，将电位表示成电阻率的显示形式，分析空间电位与单元电阻率之间的关系，克服了shima H方法中的问题[11]。李克借鉴医学上成像方法，沿着等位线修正电阻率，随着深度变大，等位线逐渐平缓，分辨率变差[12]。底青云与李克采用了类似的方法，不同之处在于借鉴地震射线追踪方法，沿着电流线修正电阻率，同样存在精度不高的问题[13]。物探异常幅度大小取决于供电源和接收装置距离待探查异常区的距离，本文提出一种采用掘进钻杆供电的方法，将激励电流传输至迎头前方，增大对异常体的激励程度。在巷道内接收，对待探测区域进行柱状剖分，建立剖分单元电阻率与异常电位差之间的近似线性关系，改变供电钻杆供电深度，形成不同供电状态下的线性代数方程组，最终得到迎头前方电阻率分布情况。

1 钻杆供电超前探测基本原理

均匀全空间点电源电位表达式有比较简单的形式[14]：

(1)

其中，R是点电源与观测位置之间的距离，ρ是介质电阻率。

根据JAMES R.WALT的研究成果，低频短距离条件下，由于供电钻杆与围岩介质存在明显的电导率差异，供电电流基本垂直于钻杆均匀流出，在钻杆长度方向上不存在流动的电流，钻杆可视为线电源[15]。线电源全空间的点位表达式为[16]：

(2)

(x0,y0,z0)是源点的坐标，x,y,z是计算点坐标。L为线源长度，线状源供电下电位等值线在平面上(z=0)的形态如图1。

图1 线电源(钻杆供电模式下)电位平面分布Figure 1 Line power supply (under drill stem power supply mode) potential plane distribution

全空间中，点电源的电位等值线为以供电点为圆心的同心圆，在供电点附近，电流密度梯度大，电位值衰减快。对于超前探测问题，在巷道掌子面供电方式下流经掌子面前方的电流密度小，对异常体激励有限。采用钻杆供电后，开孔点(对应于点电极供电处)前方电流分布均一性增强，强度也大大提高。

实现超前探测电阻率反演，需要量化电阻率变化与测量电压之间的关系。现行反演方法中，一般将待反演区域离散化并给定初始模型，根据单元电阻率梯度变化与观测数据之间的关系获得模型修正量，经过多次迭代求取最小二乘意义下的解，这种方法在未知变量较少的情况下收敛速度快，计算量小，但容易陷入局部最优解。当未知参数较多时，确定梯度方向的计算量以待反演参数个数的平方增加，而且导致模型修正量求解方程的病态性大大增加，带来求解的不稳定性，反演过程可能提前终止。

最小二乘意义下的反演过程中，梯度方向的计算实际是为了寻求某种线性关系，通过解方程更正模型。直流电场中，电位与单元电阻率关系复杂，异常电位与单元电阻率关系更有规律。全空间点电源供电下电位计算模型如图2。

图2 全空间点电源电流场中的导电球体模型Figure 2 Conductive sphere model in full space point power supply current field

点电源供电下异常球体的电位表达式为[14]：

Pn(cosθ)]

(3)

公式(3)可以看出，总电位由两部分构成：正常背景电位值和由于电流激励异常体产生的异常电位值。总场在形式上表示成如下形式：

U=U0+U1

(4)

U0是全空间背景电位，U1是异常电位，背景电位仅与全空间电阻率值和供电点、接收点之间的距离有关，异常电位形式复杂，是一个无穷级数，在形式上可进一步分解：

(5)

其中，Yn是一个与阶数和相对位置关系有关的量，qn是描述异常体和围岩电阻率差异的量。Yn在一定的观测方式下，可视为常数，异常电位只与异常体和围岩电阻率差异相关，对qn表达式做等价变换：

(6)

异常体与围岩电阻率往往相差较大，以u12的常用对数为自变量，d,r,r0均为常数情况下，qn的变化规律如图3所示：

图3 不同阶数u12与qn的关系Figure 3 Relationship between u12 and qn at different orders

图3可以看出，异常体电阻率在0.1～10变化时，异常电位值与u12存在近似的线性关系，在能获取背景电阻率的条件下，可以通过纯异常场电位差值尝试建立相对简单的近似意义下的线性代数方程组，相比需要求解雅克比矩阵及其逆矩阵的反演过程，节省极大计算量，能实现电阻率的快速反演。

2 钻杆供电超前探测反演方程

在超前探测原理一节阐述了异常电位的计算方法和反演实现基础，井下超前探测要考虑全空间因素，实现反演成像，还需要对观测数据和电阻率分布之间的具体联系做进一步明确。

图4 钻杆供电、巷道接收模式探测示意图Figure 4 A schematic diagram of prospecting under drill stem power supply and roadway receiving mode

图4展示了钻杆供电超前探测方法的施工原理图，接收电极预先放置在掌子面后方，钻杆不断向前钻进，在不同钻进深度分别供电，采集测量电位差。

由于巷道施工空间限制，采集数据观测方位十分有限，采集数据量也无法满足三维反演要求(数据量小)，井下超前探测完全的三维反演难以实现。钻杆供电条件下，钻杆钻进方向和接收数据在同一直线上，围绕该直线，异常位置对于观测数据有等值特征，将三维空间进行柱状剖分(图5)，剖分方案如下。

图5 钻杆供电、巷道接收迎头前方空间剖分示意图Figure 5 A schematic diagram of front space subdivision under drill stem power supply and roadway receiving mode

将钻孔开孔点之前的空间，以钻杆为轴心进行柱状剖分，这种剖分方式与供电、接收之间的关系最为契合。反演时，对异常体定位只考虑钻进和径向两个方向，三维空间利用对称关系简化为二维分布(图6)。

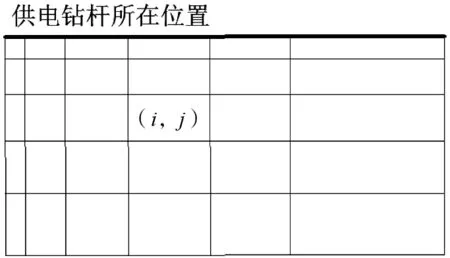
图6 三维空间剖分对应的伪二维反演网格Figure 6 3D space subdivision corresponding pseudo-2D inversion grid

伪二维反演网格采用不均匀剖分方式，远离开孔端逐渐放大网格间距。反演网格绕钻进方向旋转360°即为开孔点前方的三维空间剖分形式，点电源球状异常体电位表达式可以看出，供电电流激发条件下，异常体类似于一个次生“源”，产生的异常电位叠加于背景电位之上。线电源背景场可采用离散方式进行点电源积分叠加，不同网格单元产生的异常电位值也可以采取类似方式叠加到异常场中。将二维反演网格绕轴旋转30°,各单元均对应一部分空间体积，该空间体积用等效球体替代，将该空间体积的异常响应作为网格单元的异常响应，通过钻进深度的改变建立线性代数方程组，具体过程如下。

①对反演网格按照先行后列的顺序依次编号，记为m行，n列。

②在钻杆钻进至0.5m时(近似为0m)，采用“无穷远”电极和钻杆作为供电电极向地下供电，按照网格编号顺序分别计算电阻率差异10倍下1、2号电极之间的异常电位差，形成1行，m×n列数据。

③计算各网格对应的等效球体对2、3号电极之间的异常电位差贡献，新一行数据续接第一行，…,以此类推，计算所有网格对第24、25电极间的异常电位差，形成24行，m×n。

④钻杆钻进至10，20,……100m,依次重复步骤②-③形成新的24行，m×n列矩阵并续接；最终形成24×钻进深度个数，m×n列的总体反演矩阵。

⑤采用小四极方式，测量背景电阻率，从测量数据中减去不同供电状态下背景电位大小，得到纯异常电位；形成反演方程：

(7)

求解方程，可以得到电阻率分布的二维反演结果。

3 模型测试

为验证反演方法可行性，用正演模拟方法生成模拟数据，将设定模型与反演结果进行对比，通过对比结果对反演成像方法优劣进行评价。超前探测过程中，断层、陷落柱是比较常见的构造导水通道，采空区和老窑巷道是比较常见的储水空间，陷落柱和采空区分别是比较典型的点状、面状构造，分别用陷落柱和采空区两种模型，说明钻杆供电超前探测反演效果。

3.1 陷落柱模型超前探测反演

按图4所示的施工方法，在巷道中布置25个接收电极，间隔4m，以开孔点为坐标原点，设立模型如(图7)。

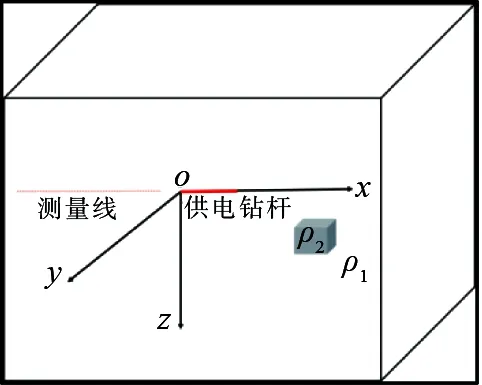
图7 钻杆供电-巷道接收陷落柱超前探测示意图Figure 7 A schematic diagram of drill stem power supply roadway receiving subsided column advanced prospecting

接收电极与钻杆在同一直线上，接收位置-2m至-98m，间距4m，，异常体为边长为15m的正六面体，中心坐标(35,20,0)，围岩电阻率100Ω·m，异常体电阻率10Ω·m，钻杆钻进深度为：0(点电极供电)、10、20、…,100m共11个深度。在各个钻进深度下，异常电位差如图8。

图8 陷落柱纯异常电位差曲线与钻进深度关系Figure 8 Relationship between subsided column pure abnormal potential difference curve and drilling depth

图(8)中每条曲线为特定钻进深度下的纯异常电位差曲线，接收数据按顺序排列，0m钻进深度接收数据编号1-24，10m钻进深度接收数据编号25-48，依此类推。数据编号为横坐标，异常电位差值为纵坐标。每条接收曲线都随编号的增加而减小，最大幅值先增大后减小，钻进深度与异常距离迎头前方距离相近时，纯异常电位差幅值最大。对计算数据按前文所提供方法反演，得到电阻率相对分布如图9。

图9 陷落柱模型反演结果Figure 9 Subsided column model inversion result

反演结果中，等值线值表示实际电阻率与背景电阻率比值的常用对数，为无量纲量，负值表示反演电阻率低于背景，正值对应高阻，绝对值大小反映偏离程度。陷落柱反演结果可以看出，反演结果异常体形态与实际存在差距，异常形态呈“豆瓣”状，图9中黑色虚线框标明了异常体在模型中的平面位置，反演异常中心与实际模型一致，分布范围有所扩大。对比反演网格不难得出结论：反演网格剖分形式决定了结果分辨率，反演网格逐渐放大方式符合分辨率随接收距离变大而减小的规律，在一定程度上平衡反演矩阵中元素数量级差异，减小反演矩阵条件数，提高稳定性，同时造成距离迎头较远处分辨率降低，分辨率与稳定性难以同时兼顾。

3.2 采空区模型超前探测反演

陷落柱是典型点状构造，反演异常中心与模型中心对应良好。采空区是巷道掘进中常见的人为遗留隐患，采空区在平面上呈面状分布，空间分布如图10所示。

图10 采空区超前探测模型示意图Figure 10 A schematic diagram of worked-out area advanced prospecting model

供电、接收方式与陷落柱探查相同，采空区模型为厚度5m的板状体，x方向30～70m，y方向10～50m，围岩电阻率100Ω·m，异常体电阻率10Ω·m。钻杆钻进深度：0(点电极供电)、10、20、…,100m共11个深度。各钻进深度下，异常场电位差如图11。

图11 采空区纯异常电位差曲线与钻进深度关系Figure 11 Relationship between worked-out area pure abnormal potential difference curve and drilling depth

采空区纯异常电位差曲线与陷落柱类似，在钻杆钻进至采空区边界时，纯异常电位幅度最大，采空区与陷落柱在模型设计上，只有分布范围差异，激发方式和接收方式并无显著改变，异常电压响应只在数值上存在差异，规律上变化不明显。对数据进行处理(图12)。

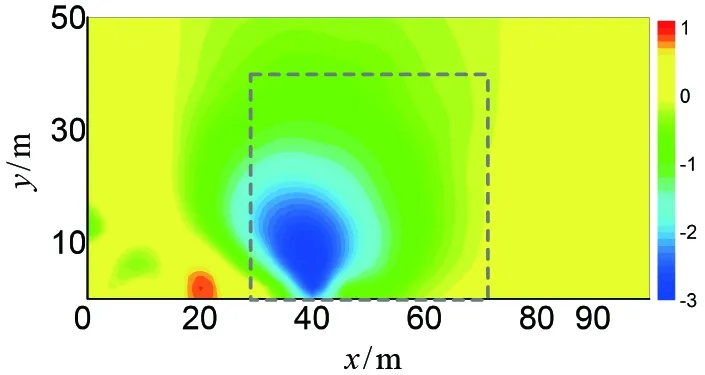
图12 采空区模型的反演结果Figure 12 Worked-out area model inversion result

图12为图10采空区模型的反演结果，图中黑色虚线框为模型中采空区设定位置，蓝绿色区域为数据反演结果，与陷落柱反演结果不同，采空区模型反演并没有明确的异常中心，反演结果异常最突出处为采空区靠近开孔点一角，其它位置异常幅度减弱，总体可大略判断范围，但分辨率不高。

3.3 采空区超前探测实例

为了验证探测方法的可行性和实用性，针对采空区模型开展了一次实验，在山西某矿工作面巷道掘进过程中，迎头前方约50m处存在已知采空区，采空区范围明确。采用本文所陈述的方法，利用钻杆供电，在巷道中布置接收电极16个采集电压数据，对测量数据进行反演，得到的反演结果和实际情况对照如图13。

图13给出了山西某矿实际采空区超前探测反演结果，紫色方框为该矿已知采空区，坐标原点为钻孔开口位置，蓝绿色区域为反演异常区域，从反演结果可以看出，反演异常区对实际采空区的反映效果与数值模拟类似，反演结果异常最大值处位于采空区边界靠近钻杆位置，偏离钻杆更远区域分辨率变差，但反演结果总体能体现采空区位置。

4 结论

①直流电场激发情况下，低阻/高阻异常体激发的异常场幅度在较大范围内和其本身电阻率与背景电阻率比值的常用对数有近似线性关系，这构成了根据异常电位差进行快速反演的基础。

②从正演模拟结果看到，固定供电状态时，纯异常电位差远离异常体时快速减小，通过推进钻杆，增加供电深度方式，可以提高异常幅度。增加对异常激励，有助于辨识异常。

③超前探测反演结果分辨率和可靠性对反演网格的要求相互矛盾，该矛盾主要由观测方式缺陷造成，数据测量在同一直线且远离异常体，在本质上不利于取得好的处理效果。

④采用钻杆供电方式，能提升对异常体激励，基于这种探测方式的二维反演方法虽在结果上并不能完全吻合模型，但突破了常规一维解释的局限，对异常体在钻进方向和径向两个方向的位置都有了更为精确的定位。

参考文献:

[1]岳建华,李志聃.煤矿井下直流层测深方法与原理[J].煤炭学报，1994,19(4):422-429.

[2]岳建华，李志聃.矿井多极距偶极剖面法及其应用[J].煤田地质与勘探，1994,22(3):47-50.

[3]程久龙，王玉和，于师建.巷道掘进中电阻率法超前探测原理与应用[J].煤田地质与探,2000,28(4)：60-62.

[4]刘青雯.井下电法超前探测方法及其应用[J].煤田地质与勘探,2001,29(5)：60-62.

[5]韩德品,程九龙,李丹.超前探测灾害性含导水地质构造的直流电法[J].煤炭学报,2010,35(4):635-639.

[6]黄俊革,王家林，阮百尧.坑道直流电阻率法超前探测研究[J].地球物理学报,2006,49(5):1529-1538.

[7]吴小平,徐果明.利用共轭梯度法的电阻率三维反演研究[J].地球物理学报,2000,43(3):420-427.

[8]王兴泰,李晓芹.电阻率图像重建的“佐迪”反演及运用效果[J].物探与化探，1995,20(3)：228-233.

[9]Shima,H,Sakayama,T.Resistivity tomography:Anapproach to 2-Dresistivity inverse problems[C].Expanded Abstracts of 57th Annual Internat SEG Mtg,1987.59-61.

[10]Shima H.Two-dimensional automatic resistivity inversion technique using alpha centers[J].Geophysics,1990,55(6):682-694.

[11]毛先进,鲍光淑.一种适于电阻率成像的正演新方法[J].地球物理学报,1998,41(增刊)385-393.

[12]李克.医学用电位成像技术在地球物理反演中的应用[J].物探化探计算技术,1997,19(3):193-201.

[13]底青云,王妙月.电流线追踪电位电阻率层析成像方法初探[J].地球物理学报,2001,44(6):843-850.

[14]李金铭.地电场与电法勘探[M].北京：地质出版社，2005：60-72.

[15]JAMES R.WAIT,DAVID A.HILL. Theory of Transmission of Electromagnetic Waves Along a Drill Rod in Conducting Rock[J].Transactions on Geoscience Electronics,1979,19(2):21-24.

[16]徐凯军，李桐林.垂直有限线源三维地电场有限差分正演模拟[J].吉林大学学报(地球科学版)，2006，36(1)：137-147.