基于MATLAB的曲柄滑块机构的动态静力分析

李 宗，姚锦涛刘 康

（长安大学公路养护装备国家工程实验室，陕西 西安710064）

0 引言

由于曲柄滑块机构之间是低副连接，在承受同样载荷的条件下压强较低，因而可以传递较大的动力，并且曲柄滑块机构加工制造比较容易，能获得较高的精度，所以在内燃机、冲床、空压机中有广泛的应用[1]。文献[2]分别以matlab和adams为研究平台，在matlab中建立数学模型对曲柄滑块机构进行仿真，在adams中将曲柄连杆机构进行柔性化对其进行仿真分析，并对两种仿真分析方法进行比较。文献[3]应用adams完成了对曲柄滑块机构的运动学和动力学仿真。文献[4]建立了以工作行程最小传动角最大为目标的多维变量优化数学模型，采用matlab优化工具箱对曲柄滑块机构进行优化设计。文献[5]针对TH50型码垛机器人采用动态静力学方法将瞬时惯性力系转化为静力系，通过机器人整体及其子系统的力系平衡方程建立了机器人的动态静力学模型。并用matlab进行求解分析，分析结果表明了数学模型的正确性。该分析方法为分析曲柄滑块机构提供了方法。

随着构件的速度的提高，构件的惯性力不能被忽略。因此需要将构件的惯性力计入静力平衡方程中。这种方法称为动态静力分析。动态静力学分析中要计入惯性力，而为求出惯性力需知道构件的加速度。因此在动态静力学分析中首先要进行运动分析。在进行运动分析时，是假定原动构件按某种理想的运动规律来运动的。为此，本文建立了曲柄滑块机构的动态静力学分析数学模型。通过实例在matlab中编程完成对特定条件下的曲柄滑块机构的动态静力学分析。

1 曲柄滑块机构的数学模型

图1为曲柄滑块机构，曲柄的角速度为ω1，曲柄长度为l1，曲柄质量为m1，质心与其回转中心A重合，连杆长度为l2，连杆质心S2在铰链B，C的连线上，连杆质量为m2，对其质心的转动惯量为J2，滑块质量为m3，其质心与铰链C重合。图2为曲柄滑块机构各构件受力图。

图1 曲柄滑块机构简图

图2 曲柄滑块机构各构件受力图

根据图1有如下表达式：

上式中，l3为点AC之间的长度。

对（1）中的角θ进行求导有：

对（2）求导有：

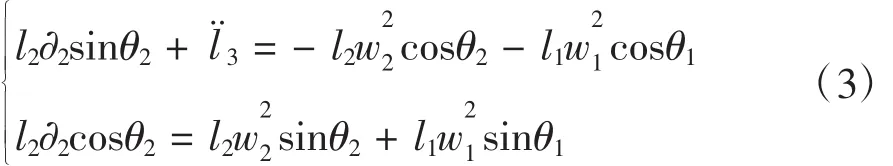
由于

对（4）式求导有

对（5）式求导得：

根据图2对构件分别列出力平衡方程和力矩平衡方程：

构件1

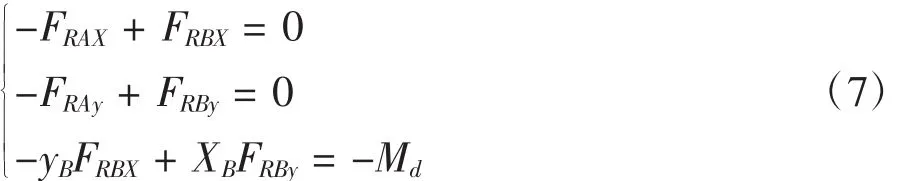
构件2

构件3

将方程组（7）、（8）、（9）写成 AR=B 的形式即为一个8×8已知矩阵，其元素与构件质心的位置有关。将曲柄的运动周期360°分成360等份，对每隔1°的360个离散位置分别求解方程，得到铰链A中的约束反力FRAX，FRAy和滑块导路中的约束反力FRDy.将B、C以及质心的位置用坐标表示为：

yB=l1sinθ1xB=l1cosθ1

ys2=（l2-z）sinθ2xs2=l1cosθ1+zcosθ2

yC=0 xC=l1cosθ1+l2cosθ2

所以系数矩阵就可以用曲柄以及连杆的长度和θ1、θ2表示。

xB-xs2= l1cosθ1-l1cosθ1-zcosθ2

xC-xsc2=（l2-z）cosθ2

摆动力即为：

2 对已知曲柄滑块机构的仿真分析

已知曲柄的角速度为w1=100 rad/s，曲柄长度为l1=50.8 mm，连杆长度为l2=203 mm，到铰链B的距离是50.8 mm.连杆质量为m3=1.36 kg，对其质心的转动惯量为J2=0.010 2 kg·m2，滑块质量为m3=0.907 kg.

通过对曲柄滑块机构建立的数学模型，通过方程组（9）、（10）、（11）得到的求解矩阵是一个 8×8 的矩阵。由于matlab具有强大的数学计算能力、简单高效的编程语言、强大的图像功能并可以进行矩阵运算、绘制函数和数据，以及强大的工具箱和方便的应用程序接口功能。同时matlab还可以进行动态系统建模、仿真。因此可以在matlab中编写求解函数。由于需要将曲柄的运动周期360°分成360等份，对每隔1°的360个离散位置分别求解方程，因此在编写matlab函数时需要用到for循环，由于在matlab的编程中是用弧度表示的，因此在编程的时候需要将角度转化成弧度。通过运行求解函数得到的求解曲线分别如图3所示。

图3 竖直方向的摆动力

从图3中可以看到，当θ1为0～30°时，竖直方向的摆动力为负且竖直方向的摆动力的绝对值逐渐增大，并在角为30°时在图中形成一个极值点；θ1为30°～120°时，竖直方向的摆动力逐渐增大，并在120°时，竖直方向的摆动力达到最大；θ1为120°～240°时，摆动力逐渐减小，并在240°时竖直方向的摆动力达到负向最大；当θ1为330°时，竖直方向的摆动力与30°时的摆动力大小相等，方向相反；在θ1为360°时，竖直方向的摆动力为0，在0～360°的范围内，形成一个闭合的曲线。

3 结束语

本文对曲柄滑块机构进行了动态静力分析，对一般情况下的曲柄滑块机构建立了数学模型。并在matlab中建立了求解函数，完成了对特定情况下的曲柄滑块的求解。当需要准确的估计惯性载荷的影响时，静态分析已经不能满足要求，因此动态静力分析为这种要求下提供了一种思路。

参考文献：

[1]何毅斌，胡荣博，刘 慧，等.基于ADAMS的曲柄滑块机构运动仿真研究[J].湖北工业大学学报，2014，29（4）：40-42.

[2]刘 俊.曲柄滑块机构动力学研究[J].上海电机学院学报，2006，9（4）：24-28.

[3]王 颖，张维强.基于ADAMS的偏置曲柄滑块机构的运动学及动力学仿真研究[J].科学技术与工程，2010，10（32）：8042-8045.

[4]金熙哲，王玉新，郭为忠，等.传动角最优的曲柄滑块机构多变量优化设计[J].上海交通大学学报，2007，41（4）：561-564.

[5]李金泉，段冰蕾.TH50型码垛机器人动态静力学分析[J].北京科技大学学报，2011，33（4）：504-508.