太阳能硅片多线切割张力控制改进研究

管永强，林罗刚，朱 阳

（台州广播电视大学高职学院，浙江 台州318000）

太阳能电池以其不消耗燃料和水等物质，使用中对环境无污染的优势，有望成为2l世纪的重要新能源之一。近年来，光伏电池产业发展迅速，块状光伏电池（一般指晶体硅光伏电池）作为目前市场上的主导产品，可分为单晶硅和多晶硅两种太阳能电池[1]。传统的硅片切割机效率低、损耗大的缺点严重制约了硅片加工行业的发展。多线切割同时可以进行几百个切片的加工，它通过缠绕在导向轴上的切割线的运动，采用研磨原理，速度快、精度高、损耗低。多线切割时，重点考虑断线故障率外，另一个质量问题是切痕的最小宽度与形位误差如平行度、角度等的精度，这些都取决于切割线的振幅和频率[2]。如果对切割线的张力控制得当，将在很大程度上解决上述问题。因此，有必要对多线切割的张力进行建模分析，找到张力控制中的问题并加以改进，从而提高多线切割的效率与精度。

1 张力原理分析

1.1 张力形成原理

在线切割过程中，材料受到牵引力，当考虑阻力等各项因素时，如图1所示，将在材料上产生张力。假设切割线张力为F0，左侧收料卷上线速度为ω1，右侧放料卷上线速度为ω2，当材料处于线弹性范围内时，可以由胡克定理得到F0[3]，F0对传送时间t求导，可以得到

式中，ε为原料的弹性模量；δ为材料的横截面积；L为原料初始牵引长度；t为原料传送时间。

图1 张力形成示意图

式（1）表明，线张力变化量与速度变化量是同向的，因此要想实现张力的控制，可以通过对速度差的调节即可，当张力需要恒定时，即调节速度差为0.

1.2 切割线的张力模型

切割机走线系统的控制目标是如何使切割线工作时具有恒定的张力。切割线绕在导线轮上，取包角为dα的任一段研究，卷辊对其产生的弹力为dp，对其产生的摩擦力为线密度为μdp，材料的线密度为ρ，如图2所示。

图2 切割线的张力模型

根据张力递增定律，在dP方向上有

在μdP方向上有

联立（2）和（3）可得

计算表明，摩擦系数μ与包角β是决定卷辊两侧张力差的主要因素。

2 切割线张力的特点分析

控制切割线上的张力保持恒定，首先可以减少切割线振动的振幅与频率，其次可以减少切割线与被切件的接触应力。与纺织业、光纤、电缆等的张力相比，切割线的张力有以下四个特点[4]：

（1）张力小。由于硅片原料价格昂贵，为了减少损耗，切割线的直径一般选用φ0.10 mm～φ0.16 mm，因此，切割线抗拉强度有限，常用张力设置如表1所示，一般在30 N上下。

表1 常用切割线张力设置

（2）张力设置要求精确。多线切割机工作时，由于切割线与工件之间的接触应力随切割线的曲率增大而增大，因此，操作时，首先要根据工件的力学强度来设置张力。其次，还要根据工件的尺寸来调整切割线的进给速度，这就需要控制切割线张力与进给速度之间的合理对应关系[5]。如果切割线张力偏大，会导致断线故障加剧，甚至有可能损坏切割机的机械系统，如果张力偏小，则效率低下，导致成本偏高。所以，多线切割机使用时，需要多方面综合考虑，精确设置合理张力。

（3）控制精度要求高。为了保证被切工件整体的厚度差异在合理的范围内，就必须使互相平行的切割线之间的张力保持致，也就必须精确控制张力的波动。

（4）张力波动的频率较高。多线切割机的切割线速度一般在400～1 000 m/min之间，由于多种因素的影响，使切割线的张力随着抖动而产生相应波动，通过对切割线张力进行信号频谱图分析，如图3所示，除了在低频段外，张力信号的衰减在全频域内都很小，信号的频带也比较宽。

图3 切割线张力信号频谱分析

3 常用张力控制方法缺陷

国内外同类产品对张力的控制多采用张力锤控制或直接式控制[6]。

3.1 张力锤控制

图4为多线切割机放线侧机械结构示意图。其原理是将一个可以在滑槽内上下移动的张力锤加在收/放线轴和加工轴间，通过张力锤的重力产生压力，并用来协调主电机与放线电机的转速。这实际上是一种开环控制。

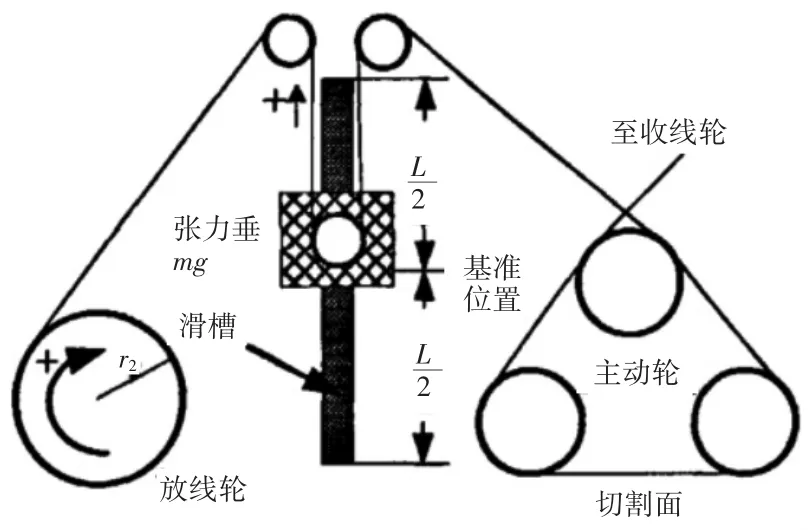
图4 多线切割机放线侧机械结构示意图

如果张力锤的质量为m，速度为VG，则可得到切割线张力F为[7]

3.2 直接式控制

直接式控制属于闭环系统控制，工作原理如图5所示。

图5 直接式控制示意图

这种直接控制方式主要用于振动频率较低的大张力场合，如绞车等，都有许多成功的案例。但多线切割机中，由于系统的运动误差、机械相关机构的跳动误差及负载效应，切割过程中张力电机产生各种不稳定现象如鸣叫、来回震荡等。

4 张力控制改进方案

由于张力锤开环控制的抗干扰能力差，直接控制的稳定性又不可靠，因此可以考虑通过机电一体化设计，降低执行机构的惯性从而降低张力振幅，实现对张力的高精度控制[8]。

4.1 结构的改进

图6所示为改进结构，用一个长为L0、角速度为ω的相对质量较小的张力摆杆（质量设为mL）替换了原来较重的张力锤，原来的张力电机换成交流伺服电机，可以对张力摆杆实施直接的转矩控制。

图6 结构改进示意图

根据动力学方程计算得到改进后的切割线张力为

式中，mL为张力摆杆质量；L为张力电机轴线到摆杆重心的距离；L0为张力摆杆长度；I为摆杆与转子的等效转动惯量；M为张力电机产生的力矩；ω0为张力电机角速度。

如果将电机转子的转动惯量等效成张力摆杆，设等效质量为mM，假定改进前后系统的加速度相同，则得到改进后切割线的张力振幅比例系数为

4.2 样机测试

以XQ300A中型多线切割机为测试样机，伺服电机采用YASKAWA公司的∑Ⅲ系列，改进后切割线的张力振幅下降为γ，得到γ曲线如图7所示。

图7 改进后张力下降的百分比曲线

试验切割单晶硅、蓝宝石等材料时，原重锤质量为6 kg左右，张力为29.3 N左右，改进后，在加速度相同的情况下，张力振幅下降了96.7%，克服了开环控制的缺陷。因此，改进方案能够保证多线切割机高效、稳定地工作，同时实现成本低、精度高的要求。

5 结束语

虽然在结构上的改进能有效控制切割线张力，但后续的检测手段还需进一步完善，如张力传感器的初始化设置问题、如何调整张力偏差等。此外，多线切割机的多电机系统如何协调控制、排线机构如何均匀收线等，对多线切割机来说均非常重要。本设计谨为后续更为完善的多线切割机设计开一先河。

参考文献：

[1]李海涛.太阳能利用研究进展[J].科技创新与应用，2016（9）：38-39.

[2]汪世益，阮超波，丁 卫.多线切割机张力扰动因素分析研究[J].机械工程与自动化，2013（1）：4-6，9.

[3]贺敬良，杜开勋，王学军.高速线切割系统张力控制研究[J].制造业自动化，2011（17）：6-8，13.

[4]张 悦.基于DSP的多线切割机张力控制系统的设计与开发[D].沈阳：东北大学，2012.

[5]朱 广.超声波振动辅助多线锯加工设备开发及实验研究[D].杭州：浙江工业大学，2015.

[6]樊尚春，乔少杰.检测技术与系统[M].北京：航空航天大学出版社，2005.

[7]吴高华.多线切割机控制系统的设计与研究[D].北京：北京印刷学院，2014.

[8]张 鹏，杨瑞峰，张学良，等.复合张力模糊控制系统设计[J].计算机测量与控制，2014（6）：1766-1769.