变速恒频双馈电机最大风能追踪控制策略

李姗姗

（江苏建筑职业技术学院机电工程学院，江苏 徐州221116）

0 引言

能源危机和环境恶化随着全球经济的高速发展，能源消耗日益增大，已经成为人类面临的两大难题。风能和太阳能由于取之不尽，用之不竭，被认为是最好的洁净绿色能源。亿万年形成的地下资源，其储量是非常有限的，且不能再生。随着全球化经济活动的加剧，能源消费的速度也在迅猛地加快，甚至超过了其潜在的开采能力，在世界范围内出现了实质性的能源危机，由此引发了人们的忧虑。如何科学有效地利用资源实现可持续发展，己经成为21世纪全球性的核心议题。

文章分析了风力发电机的运行特性，建立了双馈发电机数学模型和制定了磁场定向矢量控制策略，研究了最大风能追踪控制方法，利用双闭环PI调节控制技术实现了有功功率和无功功率解耦控制[1]。采用双PWM变换器实现了能量的双向传输。其中，转子侧变换器通过双馈发电机的矢量控制实现最大风能捕获，以及定子输出无功的独立调节；转子侧变频器与电网间的能量交换通过网侧变换器的直流环节来完成。通过Matlab/Simulink平台搭建完整的系统仿真模型，其仿真结果验证了所提控制策略的正确性和有效性。

1 风力机运行特性分析

从贝茨理论可知，风机实际捕获功率如下：

式（1）中，ρ为空气密度；v为即未扰动风速；S为在迎风情况下风机的扫掠面积；Cp为风能利用系数，Cp是叶尖速比λ和桨叶节距角α的函数，即有Cp（λ，α）。

上式中，Rw为叶片的半径；ωw为叶片旋转的角速度；nw为叶片的转速。

风力机的特性曲线如图1所示。图1为一簇风能利用系数Cp的无因次性能曲线[1]。

图1 变桨距风力机性能曲线

如果桨叶节距角α保持不变，Cp则跟叶尖速比有关，则用一条曲线来描述定桨距风力机Cp（λ）的性能。一个特定的风力机，仅有一个最佳叶尖速比—λopt（使得Cp最大），其相应的Cp称为最大风能利用系数，用Cpmax表示。

从风机的功率与转速关系的曲线来分析，建立了如图2所示的风机仿真模型。

图2 风机仿真模型

变速恒频风力发电环境中，双馈电机是风力机的负载，风机的输出作为双馈风力发电机的输入。若用状态方程对DFIG进行描述，通常将拖动转矩作为本模型的输入变量。所以在构建此风机的仿真模型时，其输出变量为机械转矩，此转矩为风机输出的机械功率变换所得。

2 最大风能追踪控制过程

变速机组最大风能捕获的目的是：在机组运行时可以最大程度地利用风能。风速一定的情况下，风力机获得的功率将功率系数来决定。一个特定的风力机，有一个最大的Cp值，同时也有一个最优的λopt值。

从公式（2）可知

当风速已知，并且风机特性曲线也已知的情况下，其最优转速很容易得知，为了实现最大风能捕获，可以对转速进行直接控制，以使机组运行在最优转速下。这种控制方法由于原理简单、目标明确，便于在实验室环境下来实现。但是由于风速变化情况比较复杂，目前还没有发现可以广泛应用的精确测量仪器，所以最大风能追踪的效果会因风速检测的误差而降低，即现场中的风速检测就成了本方法难以克服的困难[2]。

图3为在v1＜v2＜v3不同风速下风力机的输出功率和转速的关系曲线。

图3 定桨距风力机功率转速关系曲线

将每条功率—转速曲线上的最大功率点连线起来，可以从图3中得出最佳功率曲线—Pmopt曲线。从Pmopt曲线上可以得出其输出最大功率Pmmax，其表达式可以用式（4）来表示。

假设系统运行在风速v2下，最佳功率曲线的B点为风力机的稳定运行点，其对应的w2为此风速下的最佳转速和其对应的P2为最佳机械功率。即发电机的输入机械功率与系统的输出功率相等。若在某一时间点，风速升高至v3，风力机立刻由B点跳至D点运行，其输出的机械功率从P2突然升高到PD.但是由于控制系统的调节过程滞后，以及大机械惯性的作用，发电机会依然运行在风速v2曲线下的B点上，可以看出系统的输出功率小于系统的输入功率，由于输入和输出功率的不平衡，从而使发电机转速立刻升高。在这一系列变化过程中，双馈发电机沿着速度为v3下的功率波形CD运行，而风机沿着速度为v3下的最佳功率波形CB运行。当双馈风力发电系统的最优功率曲线运行到C点，风机的功率曲线也运行到C时，两个曲线相交，此时功率重新达到平衡状态，这时DFIG系统稳定运行在最佳转速w3，同时风力机输出最佳机械功率P3.

3 双馈电机转子侧定子磁场控制策略

DFIG发电系统的控制对象为输出的有功功率和输出的无功功率。通过磁场定向以及坐标变换后，DFIG定子侧电流可被分解成互相解耦的有功分量与无功分量，分别对这两个物理量进行控制即可以实现有功功率与无功功率的解耦[3]。

DFIG在m-t坐标系下的方程式为：

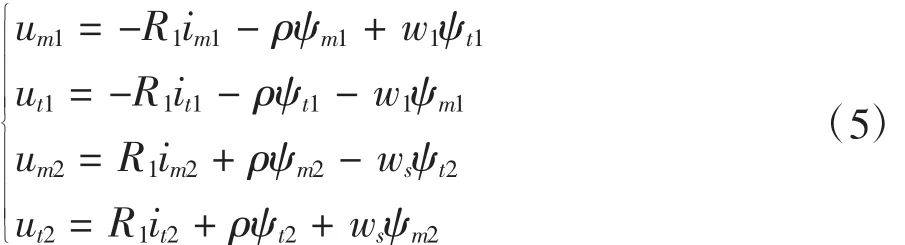
式中：um1，ut1为定子电压 m、t轴的分量；um2，ut2为转子电压 m、t轴的分量；im1，it1为定子电流 m、t轴的分量；im2，it2为转子电流 m、t轴的分量；ws=w1-wr为在m-t坐标系下转子的相对角速度。

DFIG定子输出功率方程为

定子磁场定向时，定子磁连ψ1与m轴方向一致，有约束条件：ψm1= ψ1；ψt1=0.

当DFIG接到理想电网上时u1为常数。将um1=0、ut1=-u1代入式（6）可得

通过DFIG转子侧变换器可以实现对P1、Q1的控制，从而推导出转子电流和转子电压与it1、im1的之间的关系如下：

公式（9）为实现转子电压和转子电流解耦控制的解耦项；

公式（10）为Δum2和Δut2为补偿项，是为了消除转子侧电压与转子侧电流交叉耦合的。

转子电压被分解为解耦项和补偿项后，其控制得到了简化，控制精度和动态相应的快速性得到了保证。

图4 DFIG矢量控制框图

整个控制系统采用双闭环结构，其外环为功率控制，其内环为电流控制。在外环控制中，用有功功率计算模型计算得出，用无功功率模型计算得出，将功率反馈值P1与进行比较，Q1与进行比较，通过PI功率调节器计算其差值，得出其定子电流的无功分量参考值和定子有功分量参考值和.再将进行计算分别得出转子侧电流的无功分量参考值和转子侧电流的有功分量参考值，再将和im2和it（2转子电流反馈量）进行比较，通过PI电流调节器对其差值进行调节，输出其电压分量um′2和，将电压分量再加上电压补偿分量△um2、△ut2后即可得出转子电压指令进行坐标变换，然后得到DFIG的转子电压在两相静止α2β2坐标系下的控制参数.依据物理量进行空间电压矢量脉宽调制，然后将其输出信号对双馈电机变换器进行驱动，从而实现对DFIG的控制。

4 仿真结果及其分析

变速恒频风力发电系统的Matlab/Simulink仿真模型如图4所示，其中包括DFIG模型与两个三相桥式PWM变频器模型和两个控制模块以及相关的测量模块等。系统中部分物理模型的参数设置如下[4]：

电网为线电压幅值是220 V，频率是50 Hz的三相正弦交流电。

双馈电机参数如下：额定功率为PN=2.2 kW，定子额定电压是220 V/50 Hz，同步转速n1=1 500 r/min，极对数 p=2，r1=0.435 Ω，r2′＝ 0.816 Ω，L1=0.002 H，L2′=0.002 H，Lm=0.063 9 H，转动惯量 Jg=0.089 kg·m2.

风机的参数如下：额定功率为PN=2.2 kW，最大风能系数为Cpmax=0.44，最佳叶尖速比λopt=9.6，叶片半径R=2 m，风力机与DFIG轴间变速齿轮箱增速比为N=3.84.

双PWM型变换器的参数如下：直流环节的电容C=0.008 F，直流环节的电压udc=540 V，进线电抗器L=0.005 H，等效电阻为0.01 Ω，开关频率为1 kHz.

由式（3）和（4）可得：

在风速为7.2 m/s时，系统的仿真如图5所示。

图5 亚同步速DFIG相关输出波形图

当风速为7.2 m/s时，则双馈电机在亚同步发电状态下工作，根据最大风能捕获的控制原理，发电机输出的有功功率约为1.5 kW，从图5（a）中的有功功率波形可知，仿真结果与按式（7）计算的理论值相符合。从图5（b）中相电流和相电压的波形可知电压幅值和频率始终与电网保持一致，原因是定子侧的电压接在了电网上；电流侧的波形有些脉动，原因是电流受逆变电路的影响，所以产生了脉动，因此导致无功功率以及功率因数的波形也产生了波动。

在风速为8.5m/s时，系统仿真结果如图6所示。

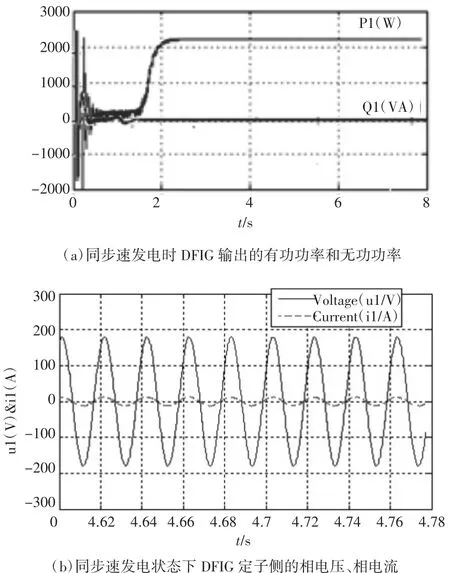
图6 同步速DFIG相关输出波形图

在风速为8.5 m/s时，按照最大风能捕获的控制原理，双馈电机工作在同步发电的状态，此时双馈电机相当于一个同步发电机，转子的励磁系统是提供直流励磁的，其输出的有功功率大概为2.2 kW，从图6（a）图的有功功率波形可见，仿真结果跟按照式（7）计算的理论值相吻合。从图7（b）图的定子电压ua的波形和定子电流ia波形可知，物理量ua与物理量ia的频率都是50 Hz，并且ua与ia几乎同相位，原因是双馈电机定子输出的无功功率很小。

在风速为10.5 m/s时，系统仿真如图7所示。

图7 超同步速DFIG相关输出波形图

当风速为10.5 m/s时，DFIG工作在超同步发电状态，根据最大风能捕获控制原理，风力机输出的有功功率约为4.3 kW.从图7（a）可知发电机定子侧输出的有功功率约为3 500 W，与理论计算值相符；无功功率在零附近波动直到稳定。通过对图5（b）和图7（b）中定子相电压和相电流的幅值大小的对比可知，由于将其接在电网上，所以发电机定子侧的电压的幅值、频率始终保持与电网一致，从而其输出量出现了恒频的特性，但随着风速的增大以及输出功率的增加，电流的大小也随之增大。

根据最大风能捕获原理，总结如下：第一，从定子侧电压和电流的波形可知，定子侧的电压幅值以及频率始终保持恒定，并且电流频率也保持恒定，但其幅值随着风速（电机转速）的变化而发生变化，其功率因数较高；第二，当定子电流或其有功功率发生变化的时候，在定子侧的无功功率却保持了恒定，即双馈发电机的有功功率以及无功功率实现了独立解耦；第三，由于双PWM变频器的协调控制，既可通过双馈发电机的励磁电源为转子馈入能量，又可将多余的转子能量回馈到电网上，从而实现了转子侧功率因数的双向流动。

5 结束语

本文从风力机的特性出发，分析了最大风能追踪的原理，从双馈电机的结构出发，分析了定子磁场定向矢量控制的方法，从而实现了定子侧的有功功率以及无功功率的解耦控制。本文建立了变速恒频风力发系统的仿真模型，并且对此系统进行了全面的仿真研究，通过控制转子侧的电压幅值和相位以及频率，实现了有功功率、无功功率和转矩的控制，从而使控制变得简单并可行。随着风速的变化，DFIG机组能可靠地进行追踪控制，并且可以最大程度地将风能转化为电能，显著地提高了风力发电机组的效率以及风能利用率。

参考文献：

[1]陈伯时.电力拖动自动控制系统：运动控制系统[M].3版.北京：机械工业出版社，2003：56-70.

[2]武喜春，马志云.双馈电机稳态分析与仿真[J].电机电器技术，2000（5）：12-15.

[3]刘其辉.变速恒频风力发电系统运行于控制研究[D].杭州：浙江大学，2005.

[4]刘其辉，贺益康，卞松江.变速恒频风力发电机空载并网控制[J].中国电机工程学报，2004，24（3）：6-11.