深水自升式平台波流载荷分析研究
2018-05-07蒙占彬王西录樊敦秋田海庆
蒙占彬 ,王西录 ,樊敦秋 ,田海庆
(1.钦州学院机械与船舶海洋工程学院,广西 钦州535011;2.中国石油海洋工程公司钻井事业部,天津300280;3中石化胜利石油工程有限公司钻井工艺研究院,山东 东营257000)
0 引言
作为海洋油气勘探开发应用最普遍的装备,自升式平台有多条可移动升降的支撑桩腿,如图1所示。当平台拖航到达海上工作地点就位后,其支撑桩腿将下降至海底,然后开始将平台提升到海面以上足够的高度,以避免在发生风暴时,波浪、海流对平台的破坏。根据桩腿结构型式不同一般分为壳体式桩腿自升式平台和桁架桩腿自升式平台。壳体式桩腿适用水深范围不超过60 m[1],受到桩腿强度和刚度的限制,深水自升式平台都采用桁架桩腿。

图1 自升式平台图片
桁架桩腿作为自升式平台的主要承载结构,由弦杆(含齿条)、水平撑及斜撑等组成,如图2所示,其支撑平台主体在海上进行作业,不仅承受平台自重,还受到波浪、海流等环境载荷作用[2]。国内外许多文献论述了海洋环境载荷计算的理论方法[3-8],本文对深水桁架桩腿自升式平台所受的波流载荷进行分析研究。

图2 桁架桩腿结构
1 波流载荷计算
1.1 波浪载荷
在海洋工程结构物波浪载荷计算中,将结构物根据特征尺度D与波长L的比值分为小尺度物体和大尺度物体。一般以D/L≤0.2作为小尺度物体;D/L>0.2称为大尺度物体。大尺度物体必须考虑绕射效应,即物体的自由表面效应和相对尺度效应。由于自升式平台桁架桩腿属于小尺度构件,可采用Morison公式进行波浪载荷计算:

式中:Fw为垂直作用于单位长度构件上的波浪力;FD为单位长度上的拖曳力;FI为单位长度上的惯性力。

式中:ρ为海水密度;CD为拖曳力系数;A为单位长度构件在垂直于矢量方向上的投影面积;un为与构件轴向垂直的相对速度矢量。

式中:CM为惯性力系数;V为构件单位长度的排水体积;u˙n为垂直构件轴线水质点加速度分量。
1.2 海流载荷及波流耦合计算
海流速度随时间变化缓慢,因此在工程设计中,为简化起见,海流被当作稳定的流动,对平台的作用仅仅是拖曳力[3]。深水自升式平台桁架桩腿水下构件受到的海流载荷可按式(4)进行计算。

式中:us为流速;其余符号意义同式1、2.
在实际工况中,因为海流载荷和波浪载荷是同时作用在结构上的,所以在实际计算中需要考虑波流耦合作用,波流耦合下拖曳力计算公式如下:

式中:Fd为垂直作用于单位长度构件上的拖曳力;其余符号意义同式1~4.
1.3 桩腿构件的水动力系数
深水自升式平台桁架桩腿波流载荷计算的关键是选取合适的波流载荷拖曳力系数CD和惯性力系数CM,可以由势流理论并结合其截面形状和运动方向来计算确定。但在实际情况中,系数CD和CM还与构件表面的粗糙度、雷诺数以及周围结构的间隔相关,因此可以通过试验或者根据以往的经验进行确定。
CCS《海上移动平台入级规范》(2012)对圆柱形构件仅给出了参考值范围:CD=0.6~1.2,CM=1.3~2.0.SNAME(美国船舶与海洋工程协会)对圆管构件(D<1.5 m)的水动力系数给出了推荐值如表1所示。

表1 圆管构件的水动力系数
桁架桩腿水平撑、斜撑、内撑均为圆管构件,拖曳力系数CD和惯性力系数CM可按表1推荐值进行选取。目前,常用的桁架桩腿弦杆截面如图3所示,为非圆管截面,其系数不能按照表1推荐值进行选取。

图3 弦杆截面示意图
船级社相关规范对于图3所示桁架桩腿弦杆水动力系数取值也未给出具体推荐值,目前部分设计与评估中采用SNAME相关推荐值。
对于图3所示截面弦杆,相对于特征尺度Di=D+2tm,SNAME推荐拖曳力系数CDi可按下式进行计算:

式中:θ为波浪入射角度,如图3所示;CD0为管构件的拖曳力系数,按表1取值;CD1为相对于投影直径W,在垂直于齿条板的水流方向上的拖曳力系数,可按下式进行取值:

对于图3所示桁架桩腿弦杆,SNAME推荐惯性力系数CMi=2.0,等效面积π/4,可应用于所有水流入射角度和构件表面状况。
2 桁架桩腿波流载荷数值计算模型
对自升式平台桁架桩腿波流载荷进行数值计算时,可以采用桁架桩腿“详细模型”和“等效模型”。
2.1 详细模型
桩腿弦杆、斜撑、水平撑等所有构件分别使用自己的莫里森特征值来建立模型,如式6~7所示:

式中:CD为拖曳力系数;D为构件直径;CDi为独立构件i的拖曳力系数;Di为独立构件i的等效直径。

式中:CM为惯性力系数;A为构件面积;CMi为独立构件i的惯性力系数;Di为独立构件i的等效直径。
2.2 等效模型
桁架桩腿的一个节距的水动力模型由一个位于实际桩腿几何中心位置处的垂直管构件来进行等效,相应的等效莫里森特征值:

其中:
式中:CDe为等效惯性力系数;Ce为桩腿的等效直径,建议取;CDei为独立构件i的拖曳力系数的等效值;CDi为独立构件i的拖曳力系数;Ci为构件i的特征尺度;li为构件i节点中心到节点中心的长度;s为桩腿一个节距的长度;αi为水流动方向和构件i轴线投影到一个水平面后之间的夹角,如图4所示;βi为构件i从水平面倾斜的角度,如图4所示。
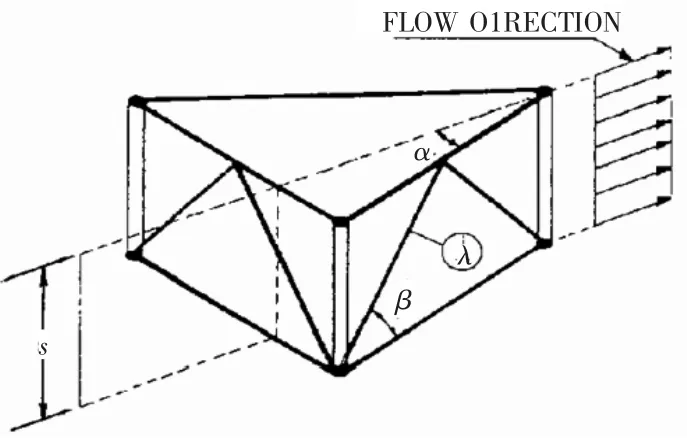
图4 桁架桩腿波流载荷计算模型
对于水平和垂直构件,CDei可进行适当简化。
对垂直构件(如弦杆):

对水平构件(如水平撑、水平内撑):

式中:CMe为等效惯性力系数;Ae为桩腿单位高度上的等效面积,可计算为(∑Aili)/s;CMei为独立构件i的惯性力系数的等效值;CMi为独立构件i的惯性力系数;CMi为独立构件i的等效面积,Ai可计算为πD2i/4.
3 算例分析
3.1 平台参数与作业环境条件
以某深水自升式平台桁架桩腿为例,采用“详细模型”与“等效模型”计算波流载荷,并对结果进行对比分析。该自升式平台为三桩腿型式,作业工况下的可变载荷为4 500 t,自存工况可变载荷为2 900 t.
平台在不同作业水深下,作业工况和自存工况的环境参数见表2.计算工况与相应水深、波高、周期、流速等参数如表2所示。

表2 计算工况与相应参数
3.2 计算模型
采用ANSYS软件建立桩腿等效模型,利用PIPE59单元模拟等效桩腿。建立的等效桩腿模型和详细桩腿模型如图5所示。

图5 桩腿计算模型
3.3 计算结果
对不同水深与不同波浪、海流工况下桩腿波流载荷进行计算,相应的计算最大波流载荷如表3所示。

表3 桩腿等效模型波流载荷计算结果

表4 桩腿详细模型波流载荷计算结果
将不同工况下采用桩腿“详细模型”和“等效模型”计算的波流载荷结果进行分析,如图6所示。


图6 不同工况计算波流载荷对比分析
从图6可以看出:采用桁架桩腿“等效模型”计算的波流载荷较“详细模型”计算的波流载荷要小,约为“详细模型”计算的波流载荷的80%左右。
4 结论
本文进行了桁架桩腿自升式平台波流载荷计算方法及计算模型分析研究,得到以下结论:
(1)桁架桩腿属于小尺度构件,其波流载荷可采用Morison公式进行计算;
(2)可采用“详细模型”与“等效模型”计算波流载荷,“等效模型”建模方法较“详细模型”简单;
(3)采用桁架桩腿“等效模型”计算的波流载荷较“详细模型”计算的波流载荷要小,约为80%左右;建议在桁架桩腿波流载荷计算中采用“详细模型”进行计算。
参考文献:
[1]汪张棠,赵建亭.自升式钻井平台在我国海洋油气勘探开发中的应用和发展[J].船舶,2008,19(1):10-15
[2]朱亚洲,孙承猛,王 凯,等.风暴条件下自升式平台桩腿强度对节距敏感性分析研究[J].船舶,2015,26(5):51-58.
[3]孙东昌.海洋自升式移动平台设计与研究[M].上海:上海交通大学出版社,2008:74-75.
[4]Watanabe E,Maruyama T,Tanaka H,et al.Design and construction of a floating swing bridge in Osaka[J].Marine structures,2000,13(4):37-58.
[5]聂孟喜,王旭升,王晓明,等.风浪流联合作用下系统系泊力的时域计算方法[J].清华大学学报(自然科学版),2005,44(9):14-17.
[6]邹志利,曹慧军.风浪流作用下系泊船系缆力和碰撞力的数值模拟[J].中国海洋平台,2002,17(2):22-27.
[7]Bisht R S,Jain A K.Wind and wave induced behaviour of offshore guyed tower platforms[J].Ocean engineering,1998,25(7):51-59.
[8]Datta T K,Jain A K.Response of articulated tower platforms to random wind and wave forces[J].Computers&Structures,1990,34(1):137-144.
