系列平行图和Meredith图的无循环边着色

张卫标，谢德政

(1.商丘学院 计算机工程学院，河南 商丘 476000；2.重庆大学 数学与统计学院，重庆400044)

1 引言和预备知识

本文考虑有限、无向的简单图.设图G=(V，E)，分别用 V(G)、E(G)、Δ(G)和 δ(G)表示图 G 的顶点集、边集、最大度和最小度，EG(v)、dG(v)和NG(v)分别表示G中与顶点v关联的边集、顶点v的度和与v相邻的顶点的集合.图G的无循环边着色是一个映射c：E(G)→C={1，2，…，k}，满足

(i)c(uv)≠c(vw)，uv、uw∈E(G)；

(ii)图G中不含双色圈.

图G的无循环边色数是指对图G进行无循环边着色所用的最少的色数，记作a′(G).

图G的无循环边着色是在无循环着色的基础上研究的，Alon等[1]提出猜想：对任意图G，有a′(G)≤Δ(G)+2，并且证明了a′(G)≤64Δ(G).之后，关于图的无循环边色数取得了很多成果[2-8].文献[2]证明了a′(G)≤16Δ(G).文献[3]证明了对于非正则连通图G，当Δ(G)=3时，a′(G)=3或4.文献[4]证明了对任意伪 Halin 图 G，当 Δ(G)≠3 时，有 a′(G)= Δ(G).文献[5]证明了对任意平面图 G，a′(G)≤Δ(G)+25.文献[6]对几类特殊图证明了Alon猜想.文献[7]证明了完全二部图 Kp2，p2满足a′(Kp2，p2)≤Δ(Kp2，p2)+2，p为奇素数.文献[8]研究了一些星图的无循环边色数.本文基于图的结构性质，利用数学归纳法和构造法研究系列平行图和Meredith图的无循环边着色.

定义1[9]在图G的边uw上插入一个顶点v(v∉V(G))，得到的图 G*称为 G的一个剖分图，其中V(G*)=V(G)∪{v}，E(G*)=E(G){uw}∪{uv，vw}.如果 H1、H2是同一个图的剖分图，则称这2个图是同胚的.

定义2[9]若图G不含与K4同胚的子图，则称图G为系列平行图(series-parallel graph)，简称为SP图.

定义3设(u，v)是图G的以顶点u为起点，以顶点v为终点的一条路，若从顶点u开始依次用颜色α、β给路(u，v)上的边交替着色，则这样的路称为双色路(u，α，β，v).

定义4设c是图G的一个边着色，(u，v)是图G的以顶点u为起点，以顶点v为终点的一条双色路(u，α，β，v)，若 c(uu′)=c(v′v)= α 或 β，其中 uu′、v′v是路上的边，则称这条路为关键双色路(u，α，β，v).

定义5[9]设Petersen图的外圈顶点集和内圈顶点集分别为{p0，p1，p2，p3，p4}和{t0，t1，t2，t3，t4}.与 pi、ti相对应的完全二部图Kk-1，k(k≥2)的二分划分别为Xi、Yi和 Ui、Vi，其中：

i=0，1，2，3，4.按如下方式用Kk-1，k(k≥2)取代Petersen图的每个顶点，连接

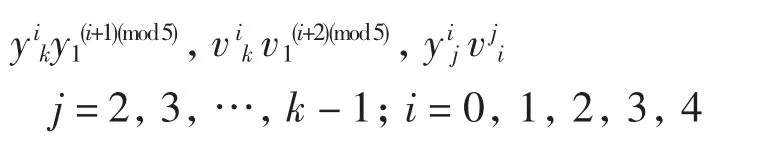
得到的k正则图称为Meredith图，记为Gk.

引理[10]设G是最小度不小于2的SP图，则下述情况至少有一种成立.

(1)G中存在2个相邻的2度点.

(2)G中存在一个3-圈xuvx，使得dG(x)=2，dG(u)=3，dG(v)≥3.

(3)G中存在一个4-圈uxvyu，使得dG(x)=dG(y)=2，且min{dG(u)，dG(v)}≥3.

(4)G中存在含顶点y的3-圈xyux和zyvz，使得dG(x)=dG(z)=2，dG(y)=4，且min{dG(u)，dG(v)}≥3.

2 主要结果

定理 1设图 G 为 SP图，Δ(G)=5，δ(G)≥2，则a′(G)≤6.

证明对图G的边数|E(G)|使用数学归纳法.设C={1，2，…，6}，由引理知|E(G)|≥7.当|E(G)|=7时，由图的结构可知结论成立.设当|E(G)|＜m(m≥8)时，结论成立，下面证明当|E(G)|=m时，结论成立.

(1)若图G中存在2个相邻的2度顶点x、y，NG(x)={u，y}，NG(y)={v，x}，构造新图G*=G-{x}+uy.显然|E(G*)|＜ m，由归纳假设，G*可以用 6种颜色进行无循环边着色，设为c*，下面将c*扩充为图G的一个无循环边着色c.令c(ux)=c*(uy)，c(xy)=α，α∈{1，2，…，6}{c(ux)，c(yv)}.由于 c(ux)≠c(yv)，因此边ux、xy、yv不着双色，故在图G中不存在关键双色路(u，c(ux)，c(yv)，v)，这样即得图 G 的一个无循环边着色c，故a′(G)≤6.

(2)若图G中存在一个3-圈xuvx，使得dG(x)=2，构造新图 G*=G-ux.显然Δ(G*)=5，下面证明当dG(v)=5时，结论成立，则当dG(v)＜5时，结论自然成立.

事实上，由归纳假设，G*可以用6种颜色进行无循环边着色，设为 c*，下面将 c*扩充为c.令c(ux)=μ，μ∈{1，2，…，6}{c*(uv)，c*(vx)，c*(uy)}，因为u是一个3度顶点，y是与u相邻的另一个顶点.这样在G中无双色圈，即得图G的一个无循环边着色c，故a′(G)≤6.

(3)若图G中存在一个4-圈uxvyu，使得dG(x)=dG(y)=2，且min{dG(u)，dG(v)}≥3.若uv∈E(G)，则与(2)类似可证结论成立.若 uv∉E(G)，令 G*=G-{y}+uv.显然 Δ(G*)=5，下面证明当 dG(u)=5 且dG(v)=5 时，结论成立，则当 dG(u)＜ 5 或 dG(v)＜ 5时，结论自然成立.

事实上，由归纳假设，G*存在一个用了6种颜色的无循环边着色c*，下面扩充c*为c.令c(vy)=c*(uv)，c(uy)=γ，γ∈{1，2，…，6}{c*(uz)}，其中uz∈EG(u).因为c(ux)≠c(uy)≠c(vy)，即在G中无双色圈，即得图G的一个无循环边着色c，故a′(G)≤6.

定理 2设图 G 为 SP图，Δ(G)≥5，δ(G)≥2，则a′(G)≤Δ(G)+1.

证明对图G的边数|E(G)|和最大度Δ(G)做双重数学归纳法.设 C={1，2，…，Δ(G)+1}，由图的结构性质有|E(G)|≥Δ(G)+2.当|E(G)|= Δ(G)+2时，结论显然成立.当Δ(G)=5时，由定理1得结论成立.设当|E(G)|＜ m(m ＞ Δ(G)+2)或 Δ(G)＜ n(n≥6)时，结论成立.下面证明当|E(G)|=m或Δ(G)=n时，结论成立.

(1)若图G中存在2个相邻的2度顶点x、y，NG(x)={u，y}，NG(y)={v，x}，设 G*=G-{x}+uy.显然 Δ(G*) = Δ(G)且|E(G*)|＜ m，由归纳假设 G*可以用Δ(G*)+1种颜色进行无循环边着色，设为c*，下面扩充c*为c.令c(ux)=c*(uy)，c(xy)=ρ，ρ∈{1，2，…，Δ(G)+1}{c(ux)，c(yv)}，由于 c(ux)≠c(yv)，因此边ux、xy、yv不着双色，故在图G中不存在关键双色路(u，c(ux)，c(yv)，v)，即得图 G 的一个无循环边着色c，故a′(G)≤Δ(G)+1.

(2)若G中存在一个3-圈xuvx，使得dG(x)=2，令 G*=G-ux.显然 Δ(G*)=n 且|E(G*)|＜ m，由归纳假设，G*可以用Δ(G)+1种颜色进行无循环边着色，设为c*，下面扩充c*为c，c是一个Δ(G)+1种颜色的无循环边着色，证明当dG(v)=Δ(G)时，结论成立，则当dG(v)＜Δ(G)时，结论自然成立.

事实上，令 c(ux)= τ，τ∈{1，2，…，Δ(G)+1}{c*(uv)，c*(vx)，c*(uy)}，因为u是一个3度顶点，y是与u相邻的另一个顶点.这样在图G中无双色圈，即得图G的一个无循环边着色c，故a(′G)≤Δ(G)+1.

(3)若 G 中存在一个 4-圈 uxvyu，使得 dG(x)=d(Gy)=2，且min{d(Gu)，d(Gv)}≥3.若uv∈E(G)，则与(2)类似可证.若 uv∉E(G)，令 G*=G-{y}+uv.显然 Δ(G*)=n且|E(G)*|＜m，下面证明dG(*u)=Δ(G)且dG(*v)=Δ(G)时，结论成立.

由归纳假设，G*存在一个用Δ(G)+1种颜色的无循环边着色c*，扩充c*为c.令c(vy)=c(*uv)，c(uy)=φ，φ∈{1，2，…，Δ(G)+1}{c(*uz)}，其中uz∈E(Gu).因为 c(ux)≠c(uy)≠c(vy)，这样在 G 中无双色圈，即得图G的一个用了Δ(G)+1种颜色的无循环边着色c，故a(′G)≤Δ(G)+1.

定理3设Gk是Meredith图，则a(′Gk)=Δ(Gk).

证明由于完全二部图Kk-1，k是Gk的一个子图，故 a′(Kk-1，k)≤a′(Gk).设 X、Y 是完全二部图 Kk-1，k的二分划，其中 X={x1，x2，…，xk-1}，Y={y1，y2，…，yk}.设

EKk-1，(kx)i={ei，1，ei，2，…，ei，k}i=1，2，…，k-1构造完全二部图Kk-1，k的边着色h：E(Kk-1，)k→{1，2，…，k}.设C=(ci)j(k-1)×k，D=(di)j(k-1)×k，其中：

在图Kk-1，k中，令h(ci)j=dij，容易验证h为图Kk-1，k的一个无循环边着色.

下面只需给出Gk的一个无循环边着色c：E(Gk)→{1，2，…，k}.对Meredith图中的每一个完全二部图 Kk-1，k均用同样的方式 h 进行着色，c|Kk-1，k=h，然后对 Kk-1，k中的 k-1 度顶点 w 的关联边 e(e∉E(Kk-1，k))进行着色，c(e)={1，2，…，k}{c(EKk-1，(kw))}.此时，在Gk中，任意以2个这样的边为起始边和终边的路之间至少有2条着不一样颜色的边，故不会形成双色圈.这样就得到了Meredith图的一个无循环边着色，所以a(′Gk)=Δ(Gk).

参考文献：

[1]ALON N，SUDAKOV B，ZAKS A.Acyclic edge coloring of graphs[J].Journal of Graph Theroy，2001，37(3)：157-167.

[2]ALON N，ZAKS A.Algorithmic aspects of acyclic edge colorings[J].Algorithmica，2002，32(4)：611-614.

[3]BASAVAARAJUM，CHANDRANLS.Acyclicedgecoloringof subcubic graphs[J].Discrete Mathematics，2008，308(24)：6650-6653.

[4]张卫标，段志霞.伪Halin图的无循环边着色[J].河南师范大学学报(自然科学版)，2010，38(2)：13-15.ZHANGWB，DUANZX.Acyclicedgecoloringofpseudo Halin-Graphs[J].JournalofHenanNormalUniversity(NaturalScience)，2010，38(2)：13-15(in Chinese).

[5]BASAVARAJU M，CHANDRAN S，COHEN N，et al.Acyclic edgecolorings of planar graphs[J].Siam Journal on Discrete Mathematics，2011，24(6)：463-478.

[6]WANG T，ZHANG Y.Acyclic edge coloring of graphs[J].Discrete Applied Mathematics，2014，167(4)：290-303.

[7]VENKATESWARLU A，SARKAR S，ANANTHANARAYANAN SM.On acyclic edge-coloring of complete bipartite graphs[J].Discrete Mathematics，2017，340(3)：481-493.

[8]SHANASBABU P，CHITHRA A V.A note on acyclic edge colouring of star graph families[J].American Journal of Computational Mathematics，2015，5(3)：253-257.

[9]阎立军，王淑栋，马芳芳.系列平行图和Meredith图的关联着色[J].高校应用数学学报，2008，23(4)：481-486.YAN L J，WANG S D，MA F F.Incidence colorings of series-parallel graphsandMeredithgraphs[J].AppliedMathematicsAJournalofChinese Universities，2008，23(4)：481-486(in Chinese).

[10]吴建良.系列平行图的列表颜色[J].山东大学学报(自然科学版)，2000，35(2)：144-149.WU J L.List edge-colouring of series-parallel graphs[J].Journal of Shandong University(Natural Science Edition)，2000，35(2)：144-149(in Chinese).