二次规划问题的比例时滞神经网络的全局渐近稳定性

程崇新，周立群

(天津师范大学 数学科学学院，天津 300387)

二次规划问题普遍存在于现实生活中，而神经网络具有内在大规模并行运算的特点，其在解决优化问题上具有巨大的潜力.Tank等[1]首次提出了解决线性规划问题的神经网络(TH网络).由于网络运行过程中时滞不可避免，相关学者提出了多种时滞神经网络来精确求解线性二次规划问题[2-5].文献[2]研究了Lagrange神经网络的收敛特性.文献[3-4]研究了常时滞Lagrange神经网络及其收敛性，并将其应用于求解二次规划问题.文献[5]研究了变时滞Lagrange神经网络求解二次规划问题.

比例时滞是一种客观存在的无界时变时滞，比例时滞系统在物理、电子与计算机科学、生物等领域发挥着重要的作用.文献[6]将比例时滞引入了细胞神经网络(CNNs).比例时滞神经网络的最大优点就是可以根据比例时滞因子的大小及网络允许的最大时滞控制网络的运行时间.目前关于比例时滞神经网络动力学行为的研究，已取得了许多成果[6-15].文献[6-9]通过构造特殊的Lyapunov泛函，利用矩阵理论及不等式技巧等方法研究了几类递归神经网络的散逸性和指数稳定性等.文献[10-13]通过构造不同的时滞微分不等式研究了具比例时滞的CNNs和杂交双向联想神经网络的全局指数稳定性，得到了一些时滞依赖与时滞独立的稳定性条件.文献[14]应用固定点定理探讨了一类具比例时滞脉ˇ冲递归神经网络的全局指数稳定性.文献[15]利用公式等研究了一类递归神经网络输入状态的均方指数稳定性.

本文提出一类比例时滞Lagrange神经网络，来求解二次规划问题的最优解.得到该网络全局渐近稳定的充分条件，该条件结构简单且易于验证.本研究所得结果是文献[5]结论的推广，将有界时滞推广到无界的比例时滞.

1 比例时滞神经网络模型

考虑如下二次规划问题

其中：u为设计变量；Q∈Rn×n为半正定矩阵，c∈Rn，A∈Rm×n，b∈Rm，并假设可行域 Ω ={u∈Rn|Au-b=0}非空.

Lagrange 函数 L(u，v)为

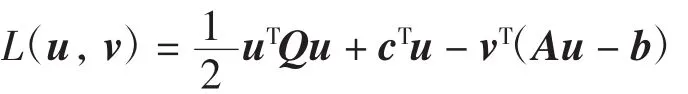
其中v∈Rn为Lagrange乘子.

由文献[16]可知，u*是二次规划问题(1)的解，当且仅当存在 v*，使得(u*，v*)满足如下 Lagrange条件

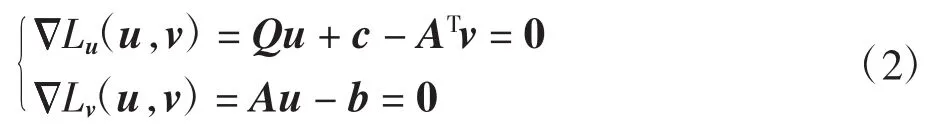
其中L为L的梯度.令

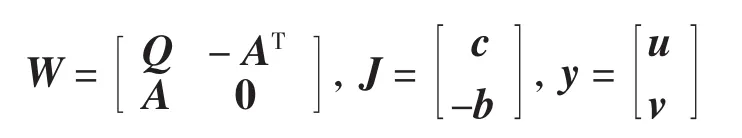
则解决问题(1)的Lagrange神经网络为

若W奇异，则网络(3)的解不稳定.为此，在网络(3)中考虑比例时滞的作用，得到如下比例时滞Lagrange神经网络

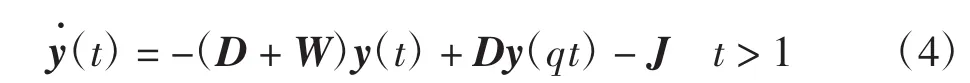
其中：D∈R(n+m)×(n+m)；q为比例时滞因子，满足0＜q≤1，(1-q)t是时滞函数，当q≠1，t→∞时，(1-q)t→∞.初始条件为 y(s)= φ(s)，s ∈[q，1]，φ(s)∈C([q，1]，Rn+m)(从[q，1]到Rn+m的所有连续向量函数构成的集合).

注1容易看出，当q=1时，网络(3)是网络(4)的特殊形式，且网络(3)和(4)具有相同的平衡点.因此可利用网络(4)来求解问题(1)的精确解，网络(4)的平衡点就是问题(1)的精确解.

注2文献[5]研究的是有界时变时滞神经网络.而本文的比例时滞神经网络(4)考虑的是一种无界时滞，所以更具有实际意义.

由文献[17]可知，u*是问题(1)的最优解，当且仅当存在 v*，使得 y*=(u*，v*)T是网络(4)的一个平衡点.

做非线性变换

则可将网络(4)等价地变换成如下形式

其中τ=-ln q＞0.初始条件为y(s)=ψ(s)=φ(es)，s∈[-τ，0]，ψ(s)∈ C([-τ，0]，Rn+m).

注3易知网络(4)和(5)具有相同的平衡点，且它们是等价的，因此网络(4)和(5)平衡点的稳定性一致.

设x*是网络(5)的一个平衡点，对网络(5)作变换 z(t)=x(t)-x*，则网络(5)变成如下形式

网络(6)相应的初值为 z(s)= ψ(s)-z*= ξ(s)，s∈[-τ，0].于是网络(5)平衡点的稳定性等价于网络(6)零解的稳定性.

定义1称系统(6)的零解是全局渐近稳定的，如果对任意初值 ξ(t)，t0≥0，满足

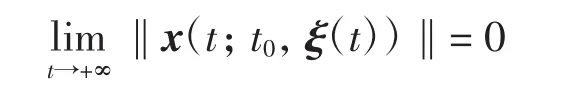
定义2称系统(4)的平衡点y*是全局渐近稳定的，如果对任意初值 φ(t)，t0≥1，满足

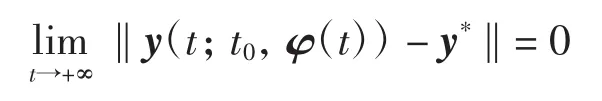
引理(Schur补定理) 对于矩阵Q=QT，R=RT，线性矩阵不等式

2 主要结果

定理若存在对称正定矩阵P、Q、R和S，使得如下不等式成立

则系统(6)的零解是全局渐近稳定的.其中：

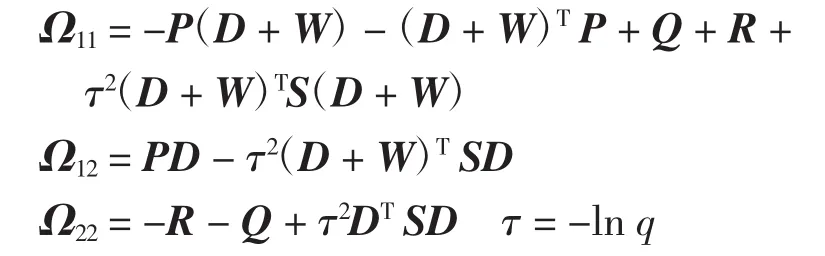
证明考虑如下正定的Lyapunov泛函

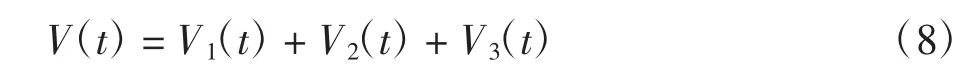
其中：

对式(8)求导

结合式(8)～式(11)可得

其中：Ω 如式(7)定义，ξ(t)=[z(t)Tz(t- τ)T]T.

林雪川表示，自己抓着黎永兰继续往河边走去，在走了一段路之后，黎永兰咬了林雪川的左大臂，林雪川于是顺势左右手一起往黎永兰的头上打去，黎永兰就往后面倒下，脑部着地。

当 z(t)≠0，z(t- τ)≠0 时，由 Ω 的定义和式(12)可知(t)＜ 0.当 z(t)≠0，z(t- τ)=0 时，由式(12)和引理可得

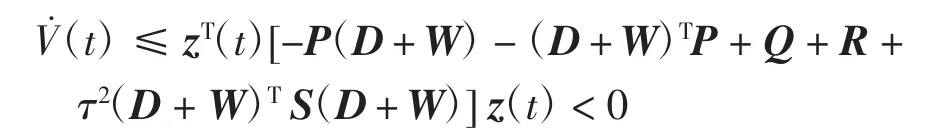
当 z(t)=0，z(t- τ)≠0 时，由式(12)和引理可得

综上可得，对每个 z(t)≠0 或 z(t- τ)≠0，都有，且当且仅当时，同时当‖z(t)‖→+∞ 时，V(t)→+∞，即 V(t)是径向无界的.因此，由Lyapunov稳定性理论可知，网络(6)的零解是全局渐近稳定的，从而网络(4)的平衡点y*是全局渐近稳定的.

3 仿真研究

算例考虑形如式(1)的二次规划问题，其中：

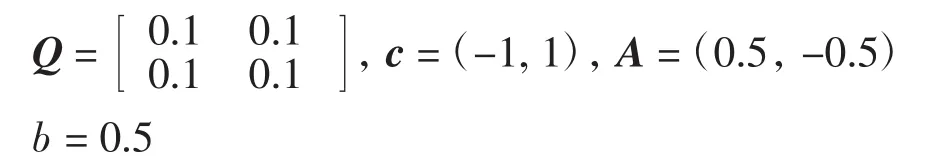
该优化问题具有唯一平衡点u*=(0.5，-0.5)T.

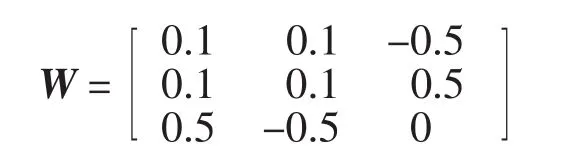
-W有3个特征值，分别为0.2、0.7071i、－0.707 1i.使用Lagrange网络模型(3)来求解优化问题(1)，利用Matlab得到时间响应曲线，见图1，可以看出神经网络呈现不稳定的趋势，显然系统的平衡点是不稳定的.

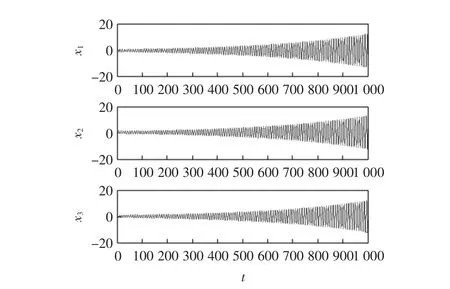
图1 模型(3)求解算例的时间响应曲线Fig.1 Time response curves of example solved by model(3)

现在考虑系统(6)，取q=0.5，由Matlab Toolbox计算，P、Q、R、S如下

由此得到

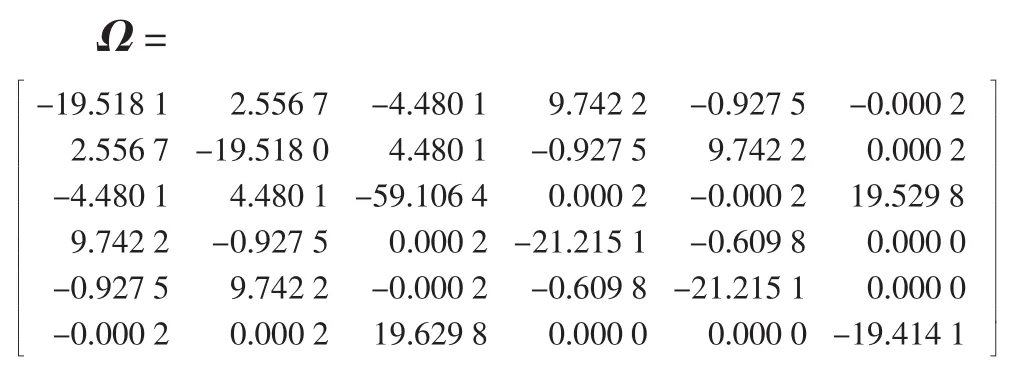
这里Ω的特征根为 λ(Ω)=-67.966 0，-31.676 1，-28.5371，-12.490 1，-10.249 1，-9.068 6，可得Ω＜0，满足定理的条件，因此系统的平衡点是全局渐近稳定的，其平衡点为(0.5，-0.5，-2)T.利用 Matlab得到时间响应曲线，见图2.可以看到该网络收敛到最优解u*=(0.5，-0.5，-2)T.

图2 当q=0.5时，模型(6)求解算例的时间相应曲线Fig.2 Time response curves of example solved by model(6)when q=0.5

注4本文的算例与文献[5]中的算例相比，除时滞项和初值不同以外，其他参数都是一致的.文献[5]的时滞项是有界时滞，而本文的时滞项是无界的时变时滞，因此文献[5]的结果不能直接应用于本文.

参考文献：

[1]TANK D W，HOPFIELD J J.Simple neural optimization networks：An A/D converter，signal decision circuit and a linear programming circuit[J].IEEE Transactions on Circuit Systems，1986，33(5)：533-541.

[2]WANG J，WU Q，JIANG D.A Lagrangian network for kinematic control of redundant robot manipulators[J].IEEE Transactions on Neural Networks，1999，10(5)：1123-1132.

[3]LIU Q S，WANG J，GAO J D.A delayed Lagrangian network for solving quadratic programming problems with equality constraints[J].Lecture Notes in Computer Science，2006，3971(14)：369-375.

[4]JIANG M H，FANG S L，SHEN Y，et al.Improved results on solving quadraticprogramming problems with delayed neural network[J].Lecture Notes in Computer Science，2007，4493：292-301.

[5]井元伟，张锐，王占山.二次规划问题的变时滞神经网络模型的全局指数稳定[J].控制与决策，2010，25(6)：921-928.JING Y W，ZHANG R，WANG Z S.Global exponential stability of neural network models with time-varying delay for quadratic programming problem[J].Control and Decision，2010，25(6)：921-928(in Chinese).

[6]ZHOU L Q.On the global dissipativity of a class of cellular neural networks with multi-pantograph delays[J].Advances in Artificial Neural Systems，2011，doi：10.1155/2011/941426.

[7]周立群.具比例时滞高阶广义细胞神经网络的全局指数周期性[J].系统科学与数学，2015，35(9)：1-13.ZHOU L Q.Exponential periodicity of high-order generalized cellular neural networks with proportional delays[J].Journal of Systems Science and Mathematical Sciences，2015，35(9)：1-13(in Chinese).

[8]ZHOU L Q.Delay-dependent exponential stability of cellular neural networks with multi-proportional delays[J].Neural Processing Letters，2013，38(3)：347-359.

[9]YU Y.Finite-time stability on a class of non-autonomous SICNNs with multi-proportional delays[J].Asian Journal of Control，2017，19(1)：87-94.

[10]周立群.一类无界时滞细胞神经网络的全局指数稳定性[J].工程数学学报，2014，31(4)：493-500.ZHOU L Q.Exponential stability of a class of cellular neural networks with unbounded delays[J].Chinese Journal of Engineering Mathematics，2014，31(4)：493-500(in Chinese).

[11]周立群.具比例时滞杂交双向联想记忆神经网络的全局指数稳定性[J].电子学报，2014，42(1)：96-101.ZHOU L Q.Global exponential stability in hybrid bidirectional associative memory neural networks with proportional delays[J].Acta Electronica Sinica，2014，42(1)：96-101(in Chinese).

[12]LIU B W.Global exponential convergence of non-autonomous cellular neural networks with multi-proportional delays[J].Neurcomputing，2016，191：352-355.

[13]ZHOU L Q，ZHANG Y Y.Global exponential stability of cellular neural networks with multi-proportional delays[J].International Journal of Biomathematics，2015，8(6)：1-17.

[14]ZHOU L Q，ZHANG Y Y.Global exponential stability of a class of impulsive recurrent neural networks with proportional delays via fixed point theory[J].Journal of the Franklin Institute，2016，353(2)：561-575.

[15]ZHOU L Q，LIU X T.Mean-square exponential input-to-state stability of stochastic recurrent neural networks with multi-proportional delays[J].Neurocomputing，2017，219：396-403.

[16]BAZARAA M S，SHERALI H D，SHETTY C M.Nonlinear Programming：Theory and Algorithms[M].New York：John Wiley，1993.

[17]XIA Y S，WANG J.A general projection neural network for solving monotone variational equalities and related optimization problems[J].IEEE Transactions on Neural Networks，2004，15(2)：318-328.