2016年阿塞拜疆奥赛试题的下界估计与推广

安徽省滁州中学 (239000)

王潇轩

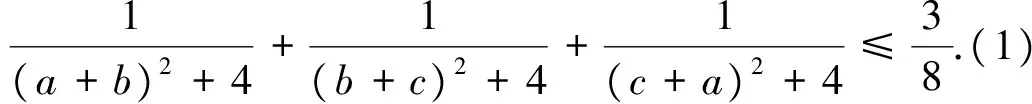
文[1]中两位老师给出该试题的证明，在微博上，安振平老师提出类似问题：

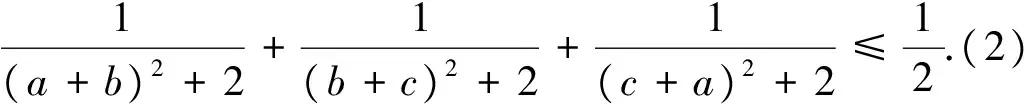
本文首先给出式(1)的下界，再将式(1)(2)作统一推广.

定理1 已知a,b,c是满足ab+bc+ca=3的正数，则

证明:式(3)等价于128+16(a+b)2+16(b+c)2+16(c+a)2-(a+b)2(b+c)2(c+a)2>0，

只需证明16[(a+b)2+(b+c)2+(c+a)2]-(a+b)2(b+c)2(c+a)2>0，

易证(a+b)2+(b+c)2+(c+a)2>(a+b+c)2，从而只需证16(a+b+c)2-(a+b)2(b+c)2(c+a)2>0，等价于证明4(a+b+c)-(a+b)(b+c)(c+a)>0，齐次化得

4(a+b+c)(ab+bc+ca)-3(a+b)(b+c)(c+a)>0，

等价于证明ab(a+b)+bc(b+c)+ca(c+a)+6abc>0，此为显然.

定理2 已知a,b,c是满足ab+bc+ca=3的正数，λ≥2，则

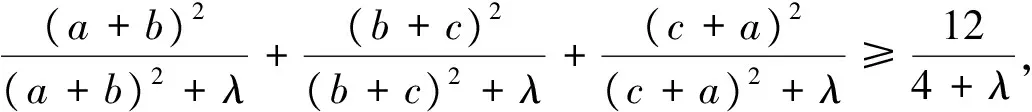
只需证明

等价于证明(4+λ)(a+b+c)2≥3[(a+b)2+(b+c)2+(c+a)2+λ(ab+bc+ca)]，

整理后知，上式等价于证明(λ-2)(a2+b2+c2-ab-bc-ca)≥0，结论显然成立.

[1]李加军,王永昌.赏析几道2016年数学奥林匹克竞赛试题[J],中学数学研究(江西),2016,10:48-50.