基于权重组合学习的无参考立体图像质量评价

潘达，史萍

(中国传媒大学 理工学部，北京 100024)

1 引言

在过去的几年里，3D电影、电视等立体视觉内容越来越多地出现在人们的日常生活当中。立体图像的质量评价方法不仅在3D视频的传输与接收中发挥重要作用，而且也是3D图像压缩的关键组成部分。在现有的立体视觉质量评价数据库中，根据左右视图失真类型和失真程度的不同，立体图像可分为对称失真立体图像和非对称失真立体图像。其中对称失真立体图像是指左右视图的失真类型和程度完全一致，他对应的质量评价是3D-IQA中首要解决的任务，因此，如何构建对称失真立体图像的质量评价模型是研究立体图像质量评价的关键。

在以往研究中，IQA可以分为全参考图像质量评价(FR-IQA)[1，2]和无参考图像质量评价(NR-IQA)[3，4]。文献[1]改进了SSIM在单视图质量评价的方法，并且基于双目竞争原理，建立了一种基于激励模型的立体图像质量评价。文献[2]引入了基于大型数据库学习的多尺度字典，在前向评估阶段，通过计算稀疏特征相似度和全局亮度相似度来估计图像质量。文献[3]提出了一种立体无参考的图像自然质量指数，他采用支持向量机训练相关的自然场景统计特征。文献[4]提出了一种无参考的深度质量评价策略，用于衡量单目和双目之间的相互作用关系，结合左右眼分数综合给出立体视觉质量分数。

尽管传统的3D-IQA方法表明，先利用优异的2D-IQA模型计算出左右单视图分数，再采用简单的平均策略也能较好地预测对称失真的立体图像质量，但左右视图之间的相关性还没有得到充分的考虑。根据实验分析，人在观看视频时，存在一种叫双眼竞争的现象，即一只眼睛会比另一只具有明显的主导优势，这说明3D图像质量感知不仅与左右眼之间的视差有关，还与双眼机制相关。受此启发，本文提出了一种端到端权重组合的无参考立体图像质量评价的深度学习网络。该网络的主要特点如下：1.深度网络将立体视觉特征作为整体评估，融入了左右视图的相关性特征；2.提出的加权集成网络能够根据图像失真情况，自我优化左右视图的能量分布。

2 立体视觉质量评价方法

众所周知，左右视图之间的相关性在3D图像感知中起着重要作用，单独计算左右视图的失真质量就缺少了对左右眼相关性的度量。因此，本文着重讨论并考虑如何将左视图与右视图结合起来进行整体质量评估。文献[4]中的理论推导表明，立体图像的质量感知可以概括为：

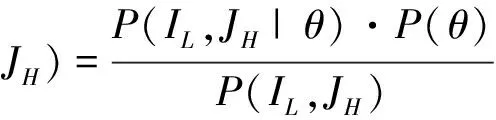
(1)

其中IL，IR分别表示左视图和右视图，θ表示3D-IQA的主观分数，P(θ)表示主观分数的先验概率分布，P(IL，IR|θ)表示在主观得分θ下，关于左视图和右视图的条件概率分布，P(IL，IR)表示3D图像的先验联合概率分布。根据贝叶斯推理，方程(1)可重新表示为：

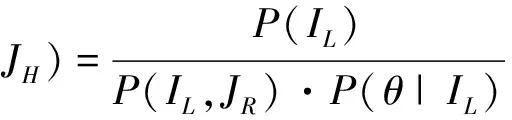
(2)

基于双眼竞争理论，人的左眼和右眼对相同光线刺激有不同的反应，这意味着在图像质量评价过程中有一只眼睛占主导地位。因此，本文改进了公式(2)：

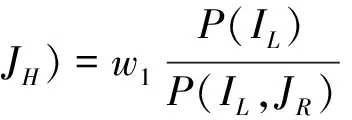
(3)

w1和w2代表左右视图的权重，本文设计了一种权重网络用以表达左右眼在评价3D图像质量中的能量分布。整个权重网络结构共6层，第一层和第三层是核大小分别为7×7和5×5的卷积层，在每个卷积层之后是2×2的最大池化层，第五层和第六层分别是大小为1024和2048个节点的全连接层。为了将网络输出值约束在0到1之间，我们选择sigmoid作为最后一层的激活函数。除最后一层外，其他层之后都选择ReLU作为激活函数。实验部分可以证明，本文提出的权重组合网络可以根据左右视图的失真内容学习自适应的能量分布。

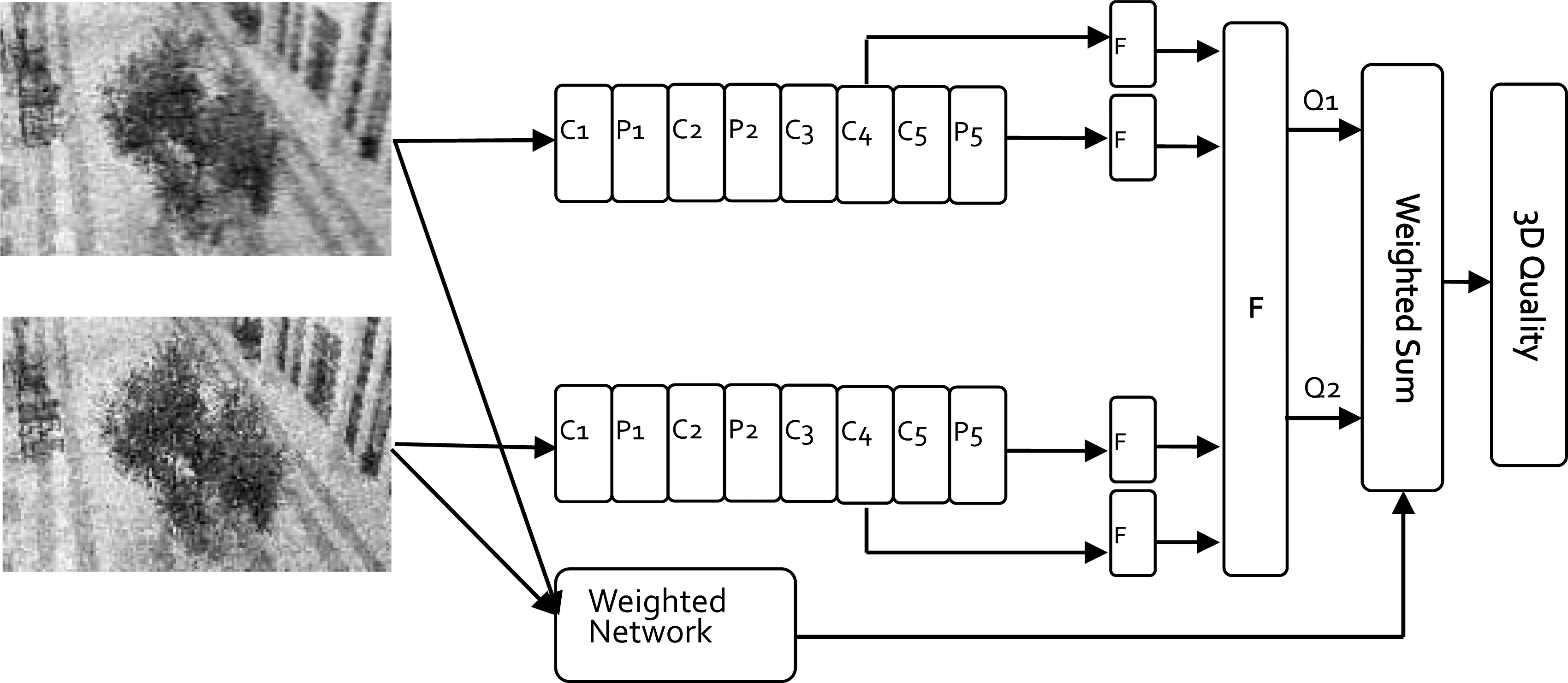
图1 本文提出的深度网络模型。C表示卷积层，P表示池化层，F表示全连接层

3 实验结果与分析

本章所有实验都在三个公开的3D-IQA数据库上进行测试，这三个库分别为LIVE 3D Phase II，Waterloo-IVC Phase I和Waterloo-IVC Phase II。这些库都包含参考图和失真图，并且图像失真覆盖不同的类型和程度。本文采用皮尔逊线性相关系数(PLCC)和斯皮尔曼相关系数(SROCC)来计算主观评分与客观评分之间的相关性用以比较各个IQA方法的性能。具体来说，PLCC是用以评估质量预测的准确率，而SROCC表示质量预测的单调性。IQA模型计算出的PLCC和SROCC的值越大，就表明该模型的性能越好。在本文所有实验中，我们将数据库的80%用于训练，剩下的20%做测试。为了避免数据划分带来的性能偏差影响，我们做了5轮交叉验证实验，整个数据库随机均分为5等份，我们将其中的一份用于测试，其余的四份用于训练，整个过程重复5次，以确保没有划分偏差。最终的质量评价分数是平均每次迭代计算的分数。

图像的最终质量评价分数是将原图中裁剪的所有224×224图像块分数取平均。为了测试图像块采样策略对最终效果的影响。本实验允许图像块重叠采样，将原始失真图像按照水平和竖直方向划分为不同数量的采样块。我们比较了三种图像划分的策略：5×5，16×10和25×15。例如，对于16×10，水平步长为(w-224)/(16-1)，w表示图像宽度。表1展示了不同数量图像块的性能比较，从表1中我们可以看出，25×15的采样组合方式性能最优。

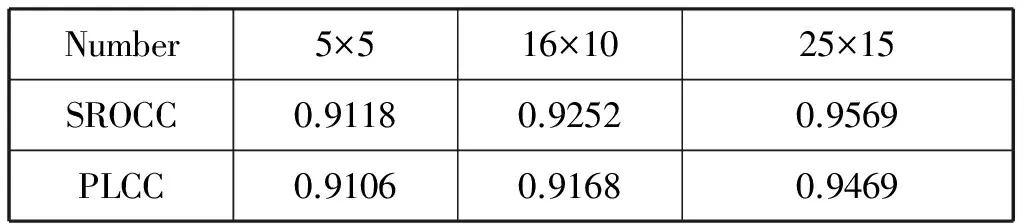
表1 在Waterloo-IVC Phase II数据库上不同数量图像块的性能比较

表2展示了本文提出的深度质量评价模型与其他方法的比较结果，其中，Mean-Net表示对左右两个分支网络预测结果直接求均值。从表2中可以看出，本文提出的方法很好地符合人的主观感知特性，而且其性能明显优于其他基于2D-IQA的方法。其中的Mean-Net均值网络比其他2D-IQA方法都高出了3%，这意味着立体质量评估深度网络能够充分表达对称失真图像的视觉感知。引入权重网络后，本文提出的方法在PLCC和SROCC两个方面都取得了最好的性能，主要是因为通过深度权重网络计算出的能量分布，能够很好地表现左右眼之间的相关性。这些结果也证明了我们提出的权重集成学习深度网络可以很好地评估对齐失真在立体视觉图像中的状态。

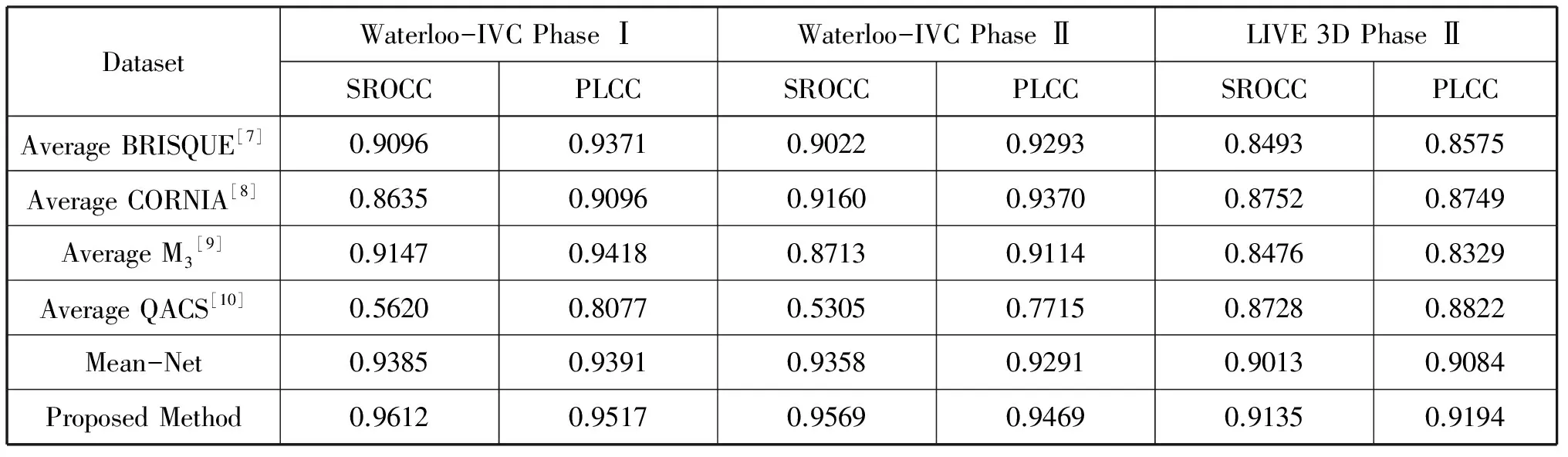
表2 各方法在3D图像数据库中的性能比较

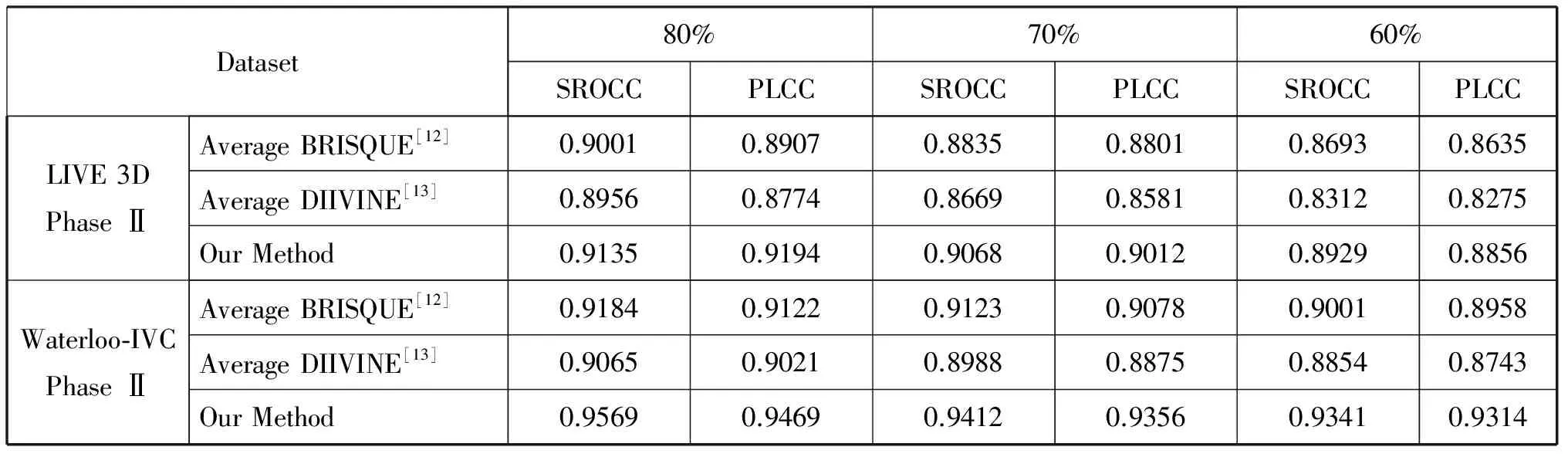
表3 数据集不同划分下的性能比较

表3展示了在三种不同的数据划分下，LIVE 3D Phase II和Waterloo-IVC Phase II两个图像库的性能结果。本文将数据集划分为80%的训练集和20%的测试集。另外两种数据的划分为70%和60%样本用于训练深度网络，其余图像用于测试。本文对每一种划分类型都随机10次，以其均值作为最终结果。结果表明，随着训练图像数量的下降，所有方法的质量评价性能都降低。但是本文提出的方法只轻微下降了0.8%，而其他方法都显着下降了4%，这证明了本文提出的方法相比其他方法，对训练图像数量的依赖性更小，在小型数据集上也能有较好的性能。

4 总结

本文提出了一种无参考的对齐失真立体图像的质量评价深度网络模型。该深度网络不仅考虑了左右视图之间的相关性，还设计了一种基于双目竞争理论的加权集成学习网络。在各个数据库上的结果表明，本文提出的方法优于其他方法，取得了与主观感知的高度一致性。

[1]Wang J，Rehman A，Zeng K，et al.Quality prediction of asymmetrically distorted stereoscopic 3D images[J].IEEE Transactions Image Processing，2015，24(11)：3400-3414.

[2]Shao F，Li K，Lin W，et al.Full-reference quality assessment of stereoscopic images by learning binocular receptive field properties[J].IEEE Transactions Processing，2015，24(10)：2971-2983.

[3]Su C C，Cormack L K，Bovik A C.Oriented correlation models of distorted natural images with application to natural stereo pair quality evaluation[J].IEEE Transactions Image Processing，2015，24(5)：1685-1699.

[4]Shao F，Tian W，Lin W，et al.Toward a Blind Deep Quality Evaluator for Stereoscopic Images Based on Monocular and Binocular Interactions[J].IEEE Transactions on Image Processing，2016，25(5)：2059-2074.

[5]Bianco S，Celona L，Napoletano P，et al.On the use of deep learning for blind image quality assessment[J].Signal Image & Video Processing，2016(3)：1-8.

[6]Liu W，Anguelov D，Erhan D，et al.SSD：Single Shot MultiBox Detector[C].European Conference on Computer Vision，2016：21-37.

[7]Mittal A，Moorthy A K，Bovik A C.No-reference image quality assessment in the spatial domain[J].IEEE Transactions Image Processing，2012，21(12)：4695-4708.

[8]Ye P，Kumar J，Kang L，et al.Unsupervised feature learning framework for no-reference image quality assessment[C].IEEE Conference on Computer Vision and Pattern Recognition，IEEE Computer Society，2012：1098-1105.

[9]Xue W，Mou X，Zhang L，et al.Blind image quality assessment using joint statistics of gradient magnitude and laplacian features[J].IEEE Transactions Image Processing，2014，23(11)：4850-4862.

[10]Xue W，Zhang L，Mou X.Learning without human scores for blind image quality assessment[C].Computer Vision and Pattern Recognition，2013：995-1002.

[11]Krizhevsky A，Sutskever I，Hinton G E.ImageNet classification with deep convolutional neural networks[C].International Conference on Neural Information Processing Systems，2012：1097-1105.

[12]Mittal A，Moorthy A K，Bovik A C.No-reference image qualityassessment in the spatial domain[J].IEEE Transactions Image Processing，2012，21(12)：4695-4708.

[13]Saad M A，Bovik A C，Charrier C.Blind image quality assessment：A natural scene statistics approach in the DCT domain[J].IEEE Transactions Image Processing，2012，21(8)：3339-3352.