纯电动汽车经济性换挡规律驱动力波动控制研究

梁晓华， 孙虎儿， 武 超

(中北大学 机械工程学院， 山西 太原 030051)

0 引 言

国内外对纯电动汽车机械式自动变速器(AMT)换挡规律、 换挡策略和换挡品质进行了广泛研究[1]， 当AMT采用经济性换挡规律时， 换挡前后车轮驱动力有较大波动， 严重影响驾驶者对车辆舒适性的体验， 减弱整车动力性能.

目前， 国内外学者对两挡ATM换挡策略进行了相关研究， 并且在机械式两挡变速器换挡过程的控制方面做了大量的工作[2]. 但是对于纯电动汽车电机转矩估测和经济性换挡规律造成的驱动力波动研究较少. 文献[2]仅从ATM换挡过程进行了分析. 文献[3]以机械式两挡变速器为研究对象， 分别对动力性换挡规律和经济性换挡规律展开研究， 利用模糊控制原理使车辆能够对工作模式自动识别， 使车辆兼顾了动力性与经济性的换挡规律. 文献[4]对经济性换挡规律进行研究， 在静态经济性换挡规律的基础上进行修正， 同时验证了静态的修正方法. 文献[5]提出了支持向量机的纯电动汽车经济性换挡控制， 并对控制策略的可行性进行了验证.

为了消除换挡前后的驱动力波动， 本文针对经济性换挡规律制定了驱动力补偿策略. 通过预测驱动电机输出转矩， 得到整车驱动力大小， 分析出消除驱动力波动的补偿转矩. 由于电机电流与电机输出转矩具有较强的关联度， 设计出基于径向基神经网的驱动电机输出转矩估测模型， 通过电机电流预测转矩， 解决了纯电动汽车电机转矩不便测量的问题. 驱动力波动控制策略极大地减弱了经济性换挡规律造成的机械式变速器换挡前后驱动力波动的影响.

1 经济性换挡规律波动分析

电机具有恒转矩和恒功率区， 为保证车辆具有连续的驱动力输出， 应该使变速器在一挡和二挡下的输出转矩特性曲线至少有一个交点[6]. 车速与驱动力曲线形成的纯电动汽车驱动特性曲线如图 1 所示，ve1为一挡时驱动电机额定转速下的车速，ve2为二挡时驱动电机额定转速下的车速.

为使驱动电机在高效率区间工作， 当驱动电机分别以一挡和二挡运行时， 在不同油门踏板开度下， 随着车速的变化电机效率值不同， 可以拟合出电机效率曲线， 由于两挡位效率曲线存在相同点， 则可拟合出经济性换挡规律， 但是经济性换挡规律会造成整车动力性能差.

如图 1 所示， 当车速ve2≥vN≥ve1， 进行一挡换二挡时， 驱动力由A点跳跃至B点， 随后延BC方向变化， 图中ABC区域无法利用驱动特性， 影响了车辆驾驶的舒适性和整车动力性. 当车速ve2≥vN≥ve1时， 换挡车速越小， 驱动力波动越大， 换挡前后驱动力波动越明显. 同样， 二挡切换一挡时， 降挡后整车驱动力由D点升至E点， 换挡前后驱动力也会出现明显波动.

图 1 某油门开度下驱动力曲线Fig.1 Tractive effort curve for the opening of a certain throttle

2 估测驱动电机转矩与驱动力

2.1 转矩估测模型

电机的电流在一定程度上可以反映驱动电机的转矩， 但由于电机的功率因素等复杂条件的影响， 电机的转矩与电流存在非线性的关系.

设非线性关系模型为[7]

y(k+1)=f[y(k),y(k-1),…,y(k-n),

u(k),…,u(k-m)]+ω(k+1).(1)

在实际应用中将模型表示为

f(x)=f0,i(x)+Δfi(x),(2)

式中：i∈{1,2,…,N}，f0,i(x)为第i个工况下的粗略估计； Δfi(x)为未知函数， 即转矩估计的不确定项.

根据纯电动汽车的动力学可得， 在第i个工况下利用电流估测转矩f0,i(x)的粗略估计为

(3)

式中：k为系数；U为电池实际电压；u为车速；r为车轮半径；y为传动比.

2.2 转矩估测不确定项逼近

由于神经网络具有任意精度逼近任意非线性函数的特点， 本文采用神经网络逼近转矩估测的不确定项[8].

(4)

高斯基函数选择[9]

(5)

式中：ci为第i个高斯基函数的中心；σi为高斯基函数的宽度.

2.3 网络学习算法

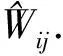
2.3.1 中心调整算法

中心调整算法以最小距离为指标， 具体步骤如下：

1) 初始化中心ch(0)， 1≤h≤H， 给出初始学习率α(0).

2) 计算第k步的最小距离

lh(k)=‖x(k)-Ch(k-1)‖,

1≤h≤H,h≠q.(6)

3) 求最小距离结点

q=arg[minlh(k),1≤h≤H],(7)

式中： arg[]表示取结点号.

4) 更新中心

Ch(k-1), 1≤h≤H,h≠q,(8)

Cq(k)=Cq(k-1)+α(k)[x(k)-Cq(k-1)].(9)

5) 重新计算第q结点的距离

lq(k)=‖x(k)-Cq(k)‖.(10)

6) 修正学习率

(11)

2.3.2 网络权值调整算法

权值视为一个向量,

Wj(k)=[W1j(k),W2j(k),…,Wij(k)]T,(12)

式中： 1≤j≤N.

设在第k步时中间层的输出向量为

φ(k)=[φ1(l1(k),ρ),…,φH(lH(k),ρ)]T.(13)

第k步， 第j个估计输出为

(14)

根据递推最小二乘法， 网络权值的调整算法为

Wj(k+1)=Wj(k)+P(k)·φ(k)·ηi(k),(15)

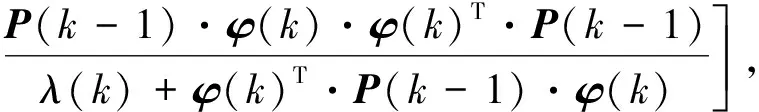
式中：P为误差方差阵；λ为遗忘因子.

2.4 整车驱动力计算

纯电动汽车的整车质量和车型保持一定时， 可以通过驱动电机输出转矩T推算出整车驱动力F， 即

(17)

式中：η为传动效率；yi为i挡位传动比；r为车轮半径.

2.5 仿真实验

根据文献[11]， 应用车辆仿真软件AMESim建立纯电动汽车整车动力系统仿真模型， 如图 2 所示. 动力系统仿真模型包括： 车辆动力学模型、 蓄电池模型、 整车控制器、 驱动电机模型和两挡机械式变速器模型[11-13]. 纯电动汽车及变速器仿真模型基本参数如表 1 所示.

表 1 纯电动汽车仿真模型基本参数

获取AMESim仿真模拟数据中的电机电流和驱动电机的输出转矩， 经过大量数据训练后[14]， 利用MATLAB进行神经网络估测驱动电机转矩.

仿真模拟纯电动汽车在复杂路面以一挡和二挡时的运行， 并分别获取其以一挡和二挡运行时驱动电机的电流和实际驱动电机的输出转矩， 得出实际转矩和估测转矩曲线， 如图 3 和图 4 所示.

图 2 纯电动汽车整车动力系统的仿真模型Fig.2 Simulation model of the power system of pure electric vehicle

图 3 一挡时复杂路面运行估测转矩和实际转矩Fig.3 Estimation of torque and torque for complex pavement in 1 gear

图 4 二挡时复杂路面运行估测转矩和实际转矩Fig.4 Estimation of torque and torque for complex pavement in 2 gear

通过对估测得到的转矩与实际驱动电机转矩进行比较可知， 估测转矩的最大偏差为4.662 N·m， 误差率为0.086， 且对驱动电机电流为 10 A 以上的转矩进行估测， 其估测误差率小于 0.09.

3 驱动力波动控制策略

3.1 驱动力波动控制流程

纯电动汽车以经济性换挡规律模式运行时， 驱动力波动控制流程如图 5 所示.

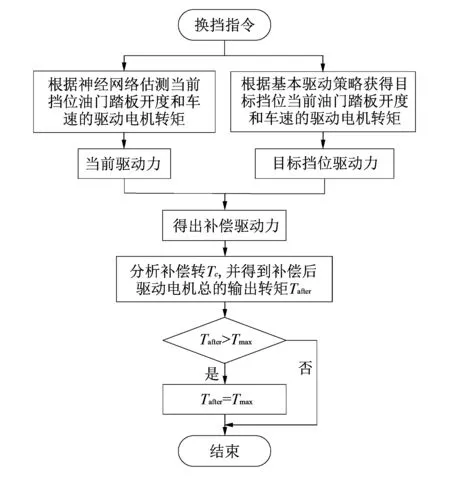
图 5 驱动力波动控制流程图Fig.5 Flow chart of tractive effort fluctuation control

3.2 升挡驱动力波动控制

如图 1 所示， 当车辆在车速满足ve2≥vN≥ve1进行升挡时， 会产生驱动力波动. 为使升挡后的驱动力从A点连续变化到B点， 减弱驱动力波动[15]， 则需要补偿的驱动力为

FcA=Ft_A-ft_B,(18)

式中：Ft_A,Ft_B分别表示车速为uup时一挡和二挡的驱动力.

二挡时， 驱动电机的转速nc_B为

(19)

式中：s为系数.

于是驱动电机转速为nc_B时的补偿转矩为

(20)

3.3 降挡驱动力波动控制

当二挡降一挡时， 如图 1 所示， 整车驱动力由D点上升至E点， 造成驱动力冲击波动. 为避免大的冲击现象， 在油门踏板开度一定的情况下， 驱动力随车速能够缓慢连续变化到E点， 可以减弱换挡的动力冲击， 车辆需要补偿的驱动力为

Fc_E=Ft_E-Ft_D,(21)

式中：Ft_E为车速在udown时一挡的驱动力；Ft_D为车速在udown时二挡的驱动力.

二挡时， 车速udown对应的电机转速nc_E为

(22)

可以得到在当前油门踏板开度情况下， 电机转速为nc_E时的补偿转矩为

(23)

综上所述， 驱动转矩的补偿策略就是对变速器挡位为二挡时的基本驱动策略进行补偿. 补偿后驱动电机总的输出转矩Tafter为

Tafter=Tb+Tc,(24)

式中：Tb为基本驱动策略的电机转矩；Tc为转矩补偿策略确定的补偿转矩.

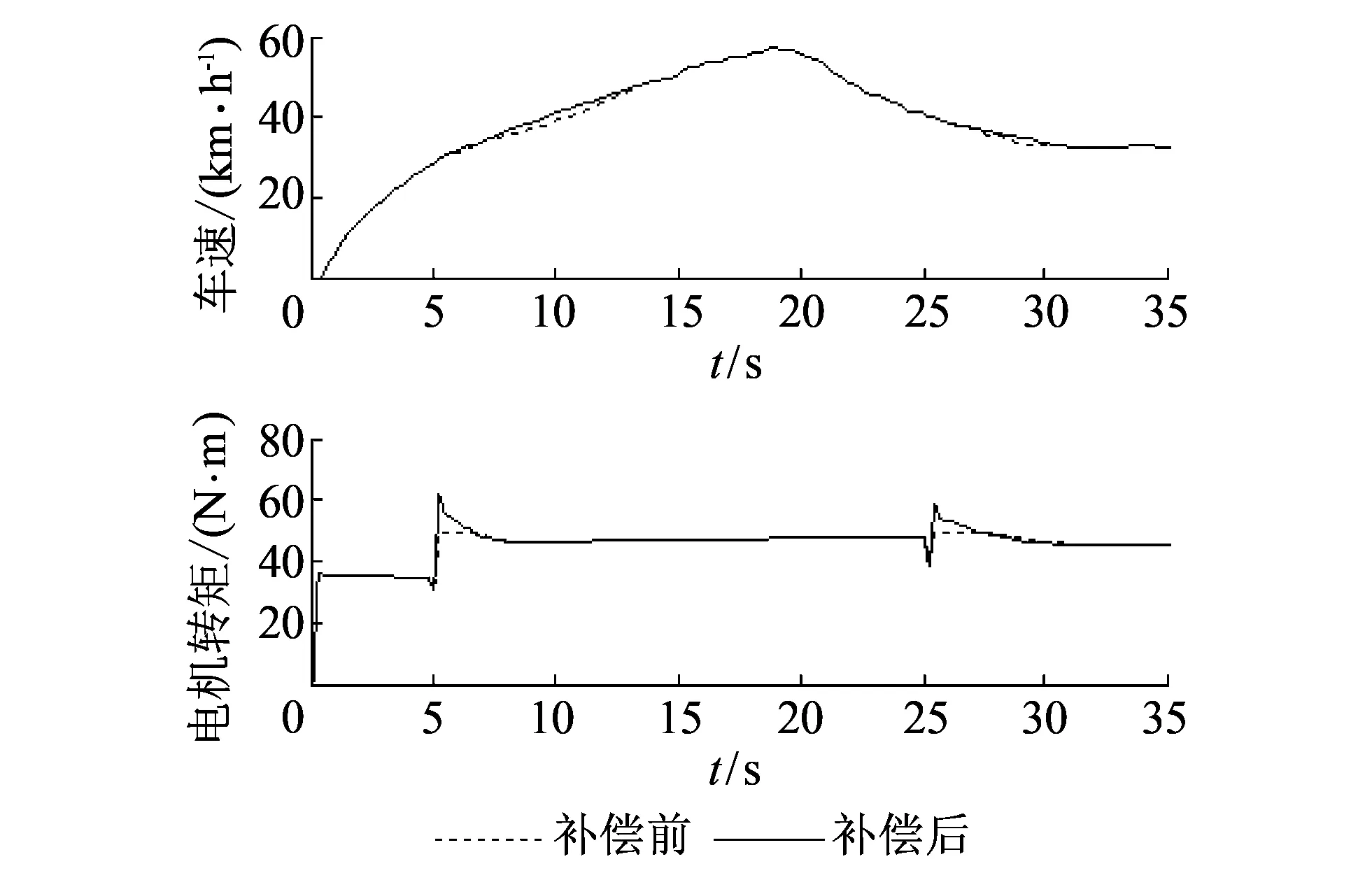
当驱动电机的最大转矩Tmax

Tc=Tmax-Tb.(25)

通过以上分析， 可得到补偿后的驱动控制策略图， 如图 6 所示. 由于驱动电机最大功率的限制， 导致补偿转矩随油门踏板开度的增大而减小.

图 6 补偿后的驱动控制策略图Fig.6 Drive control strategy after compensation

4 仿真验证

通过系统仿真模型对驱动力波动控制策略的性能进行测试， 油门踏板开度为40%且坡度为0%时的升挡仿真结果如图 7 所示. 通过对比使用驱动力波动控制策略前后的升挡车速曲线[16]， 发现在换挡时， 由于驱动力波动控制策略能够消除升挡前后的驱动力波动， 所以图 7 中补偿后的车速曲线变化更平滑， 整车舒适性和动力性都有所改善.

图 8 所示的起步和减速仿真模拟情况为： 车辆以油门踏板开度为30%起步， 在车速为30 km/h 时升挡， 车速加速到60 km/h， 当遇到10%的坡度时， 车速降低， 在车速为35 km/h时降挡. 在驱动力波动控制策略作用下， 图 8 中补偿后的车速曲线变化更平滑， 通过使用驱动力波动控制策略， 整车舒适性和动力性都有所改善.

图 7 升挡控制仿真模拟Fig.7 Simulation of up-shift

图 8 起步和减速仿真模拟Fig.8 Simulation of start and deceleration

5 结 论

针对经济性换挡规律造成纯电动汽车换挡前后驱动力波动现象的分析， 提出了驱动力波动控制策略. 利用驱动电机转矩估测算法求得电机当前驱动转矩， 对纯电动汽车的驱动力进行计算. 然后利用纯电动汽车的驱动力波动控制策略， 对二挡的基本驱动控制策略进行转矩补偿， 以此来消除或抑制换挡前后的驱动力波动.

利用AMESim软件建立纯电动汽车动力系统仿真模型， 通过仿真实验， 得到驱动电机电流和输出转矩数据， 通过大量的数据训练神经网络估测驱动电机转矩算法， 并与实验得到的驱动电机的转矩进行比较, 电机电流在10 A以上得到的估测转矩误差率小于0.09. 然后利用纯电动汽车的动力系统模型， 对驱动力波动控制策略进行验证， 结果表明， 通过使用驱动力波动控制策略， 能够减小换挡前后车轮驱动力的波动， 使换挡前后的车速平滑过渡， 整车动力性和驾驶舒适性得到了改善.

参考文献：

[1] 叶杰， 赵克刚， 黄向东， 等. 纯电动汽车无动力中断二速变速器的电机协调换挡控制[J]. 汽车工程， 2016, 38(8)： 989-995.

Ye Jie， Zhao Kegang， Huang Xiangdong， et al. Motor coordinated shift control for a two-speed uninterrupted shift transmission of pure electric vehicle[J]. Automotive Engineering， 2016， 38(8)： 989-995. (in Chinese)

[2] Liu H， Lei Y， Li Z， et al. Gear-shift strategy for a clutchless automated manual transmission in battery electric vehicles [J]. SAE International， 2012， 5(1)： 57-62.

[3] 孙冰， 熊会元， 于丽敏， 等. 两挡AMT换挡模式对电动汽车性能影响的研究[J]. 机械传动， 2015， 39(10)： 43-47.

Sun Bing， Xiong Huiyuan， Yu limin， et al. Research of the effect of two-speed AMT shift mode on electric vehicle performance[J]. Journal of Mechanical Transmission， 2015， 39(10)： 43-47. (in Chinese)

[4] 江昊， 赵韩， 黄康， 等. 纯电动汽车经济性换挡规律仿真研究[J]. 汽车工程 ， 2015， 39(10)： 43-47.

Jiao Hao， Zhao Han， Huang Kang， et al. A simulation study on the shift schedule of electric vehicle aiming at fuel economy[J]. Automotive Engineering， 2015， 39(10)： 43-47. (in Chinese)

[5] 晏伟清， 赵韩. 基于支持向量机的纯电动汽车经济性换挡控制[J]. 合肥工业大学学报， 2016， 39(4)： 451-456.

Yan Weiqing， Zhao Han. Economic shift strategy of pure electric vehicle based on SVM[J]. Journal of Hefei University of Technology， 2016， 39(4)： 451-456. (in Chinese)

[6] 周云山， 杨克锋. 两挡纯电动汽车传动系换挡规律及速比优化研究[J]. 机械传动， 2015， 39(12)： 12-16.

Zhou Yunshan， Yang Kefeng. Research of the shift schedule and ratio optimization for the transmission system of a two-speed electric vehicle[J]. Journal of Mechanical Transmission， 2015， 39(12)： 12-16. (in Chinese)

[7] Liu D， Yang G H. Neural network-based event-triggered MFAC for nonlinear discrete-time processes[J]. Neurocomputing， 2018， 272： 356-364.

[8] Alexandridis A， Chondrodima E， Giannopoulos N， et al. A fast and efficient method for training categorical radial basis function networks[J]. Transactions on Neural Networdks and Learning Systems， 2017， 28(11)： 2831-2836.

[9] Jing Y H， Yang G H. Neural-network-based adaptive fault-tolerant tracking control of uncertain nonlinear time-delay systems under output constraints and infinite number of actuator faults[J]. Neurocomputing， 2018， 272： 343-355.

[10] Talkhoncheh M K， Shahrokhi M， Askari M R. Observer-based adaptive neural network controller foruncertain nonlinear systems with unknown control directions subject to input time delay and saturation[J]. Information Sciences， 2017， 418： 717-737.

[11] Sorniotti A， Holdstock T， Pilone G L， et al. Analysis and simulation of the gearshift methodology for a novel two-speed transmission system for electric powertrains with a central motor[J]. Automobile Engineering， 2012， 226(7)： 915-929.

[12] Tseng C Y， Yu C H. Advanced shifting control of synchronizer mechanisms for clutchless automatic manual transmission in an electric vehicle[J]. Mechanism and Machine Theory， 2015， 84： 37-56.

[13] Hu J J， Ran H L， Pang T. Parameter design and performance analysis of shift actuator for a two-speed automatic mechanical transmission for pure electric vehicles[J]. Advances in Mechanical Engineering， 2016， 8(8)： 1-15

[14] 陈清洪， 秦大同， 叶心. AMT汽车动态模糊神经网络三参数换挡策略研究[J]. 汽车工程， 2010， 32(6)： 506-509.

Chen Qinghong， Qin Datong， Ye Xin. A study on the three parameter shift schedule of AMT vehicle based on dynamic fuzzy neural network[J]. Automotive Engineering， 2010， 32(6)： 506-509. (in Chinese)

[15] 傅洪， 王艳静， 冯超， 等. 一种纯电动汽车的电机-变速器动力系统[J]. 汽车工程， 2016， 38(8)： 996-1000.

Fu Hong， Wang Yanjing， Feng Chao， et al. A motor transmission power train for pure electric vehicles[J]. Automotive Engineering， 2016， 38(8)： 996-1000. (in Chinese)

[16] Kouroussis G， Dehombreux P， Verlinden O. Vehicle and powertrain dynamics analysis with an automatic gearbox[J]. Mechanis and Machine Theory， 2015， 8： 109-124.