橡胶弹簧隔振特性及其影响因素研究

黄雪涛， 李战芬， 王海霞， 钟 兵

(1. 山东交通学院 汽车工程学院， 山东 济南 250357； 2. 太原工业学院 网络中心， 山西 太原 030008)

0 引 言

橡胶弹簧隔振系统具有隔振效率高、 抗冲击能力强、 稳定性好等特点， 在工程机械和轨道交通隔振领域有着广泛的应用前景. 然而， 橡胶弹簧隔振特性的研究涉及到橡胶的材料非线性、 大变形非线性及橡胶弹簧复杂的静、 动态特性， 研究的难度较大. Schmidt等[1]建立了橡胶弹簧的力学模型； Karlsson等[2]探讨了橡胶弹簧的黏弹性模型； Sasso等[3]进行了橡胶材料等双轴拉伸试验； Ho等[4]构建了橡胶弹簧力学系统的数学模型； Liu等[5]研究了基于模型自适应控制的主动隔振技术； Platz等[6]研究了主动隔振和被动隔振的不确定性； Li等[7]基于微分技术的隔振系统进行了动力学分析； 黄雪涛等[8]研究了低速载货汽车橡胶垫块的减隔振技术； 胡振娴等[9]研究了汽车前悬架橡胶连接件的时域响应； 高俊等[10]研究了层叠式PVDF混合隔振器的隔振性能； 李玉龙等[11-12]研究了金属橡胶隔振系统的混沌响应及金属橡胶消极减振系统的响应特性； 王小莉等[13]研究了基于开裂能密度及裂纹扩展特性的橡胶隔振器疲劳特性预测技术； 杨俊等[14-15]研究了橡胶弹簧的动态特性， 构建了弹性橡胶垫的非线性模型. 前人的研究主要集中在橡胶力学特性及力学模型的构建上， 对橡胶弹簧隔振特性及其影响因素研究的相对较少. 本文以橡胶弹簧的隔振特性为研究对象， 采用理论推导、 仿真分析和试验验证相结合的方法， 研究橡胶弹簧的隔振特性及其影响因素， 为橡胶弹簧隔振系统的设计开发提供技术支撑.

1 橡胶弹簧本构方程的建立

橡胶弹簧的本构方程是描述橡胶弹簧各部件之间应力应变关系的物理方程. 橡胶弹簧由顶部的弹簧板和底部的橡胶块组成， 设橡胶弹簧的总应变为ε， 弹簧板和橡胶块的应变分别为ε1和ε2， 橡胶弹簧的总应力为σ， 橡胶块和弹簧板的弹性模量分别为E1和E2， 橡胶块的黏弹性系数为η1， 则橡胶弹簧的本构模型如图 1 所示.

橡胶弹簧的应力应变关系可以表示为

(1)

则其本构方程为

(2)

图 1 橡胶弹簧的本构模型Fig.1 Constitutive model of rubber spring

2 橡胶弹簧隔振特性的理论计算

橡胶弹簧的隔振特性是表征系统的输出与输入比值的物理量. 为了研究的方便， 假设施加在橡胶弹簧上的激励为正弦载荷， 而橡胶弹簧用单自由度有阻尼系统来表示， 则由振动学知识可知， 其输出激励也为正弦载荷. 橡胶弹簧隔振系统的隔振原理如图 2 所示.

图 2 橡胶弹簧的隔振原理Fig.2 Vibration isolation principle of rubber spring

橡胶弹簧隔振系统的绝对传递率为

(3)

橡胶弹簧隔振系统的动力放大系数为

(4)

相对阻尼系数可以表示为

(5)

式中：A为激励幅值；λ为激励与响应的频率比；U为响应幅值；FT为响应力幅值；F0为激振力幅值；C为橡胶弹簧的粘性阻尼系数；k为橡胶弹簧的刚度；m为橡胶弹簧隔振系统的质量.

由式(4)， 式(5)可知， 影响橡胶弹簧隔振特性的因素主要包括激励条件、 橡胶弹簧隔振系统的质量、 橡胶弹簧的刚度及阻尼.

3 橡胶弹簧隔振特性的仿真计算

橡胶材料为典型的非线性黏弹性材料， 为了研究橡胶材料的应力应变关系， 利用万能试验机对指定的橡胶材料进行单轴拉伸、 双轴拉伸和平面拉伸试验， 得到橡胶材料的力学特性数据如图 3 所示.

图 3 橡胶材料力学特性数据Fig.3 Mechanical property data of rubber material

依据橡胶弹簧的具体结构参数和橡胶材料的力学特性， 利用大型有限元仿真软件ABAQUS构建橡胶弹簧隔振系统的有限元仿真模型， 如图 4 所示.

图 4 橡胶弹簧有限元模型Fig.4 Finite element model of rubber springs

为了研究橡胶弹簧的隔振特性， 对橡胶弹簧隔振系统施加正弦位移激励， 其大小可以表示为

X(t)=X0sin(ω0t+φ0),(6)

式中：X(t)为位移激励；X0为位移激励的幅值，X0=1 mm；ω0为位移激励的角频率，ω0=62.8 rad/s；φ0为位移激励的初相位，φ0=0. 橡胶弹簧隔振系统的动态响应如图 5 所示.

由图 5 可知， 橡胶弹簧的动态响应也近似为正弦曲线， 其振动幅值为0.26 mm， 故橡胶弹簧隔振系统的绝对传递率为0.26.

图 5 橡胶弹簧动态响应Fig.5 Dynamic response of rubber spring

4 橡胶弹簧隔振特性的影响因素

影响橡胶弹簧隔振特性的因素主要包括激励条件、 橡胶质量、 刚度及阻尼. 为了研究这些因素对橡胶弹簧隔振特性的影响规律， 结合试验仿真方法， 研究正弦激励下橡胶弹簧动态响应的变化规律.

4.1 激励条件对隔振特性的影响规律

为了研究橡胶弹簧隔振特性随激励条件的变化规律， 保持橡胶弹簧隔振系统的质量、 刚度、 阻尼不变， 得到不同激励频率下的橡胶弹簧绝对传递率如表 1 所示.

表 1 不同激励频率下橡胶弹簧的绝对传递率

橡胶弹簧绝对传递率随激励频率的变化关系如图 6 所示.

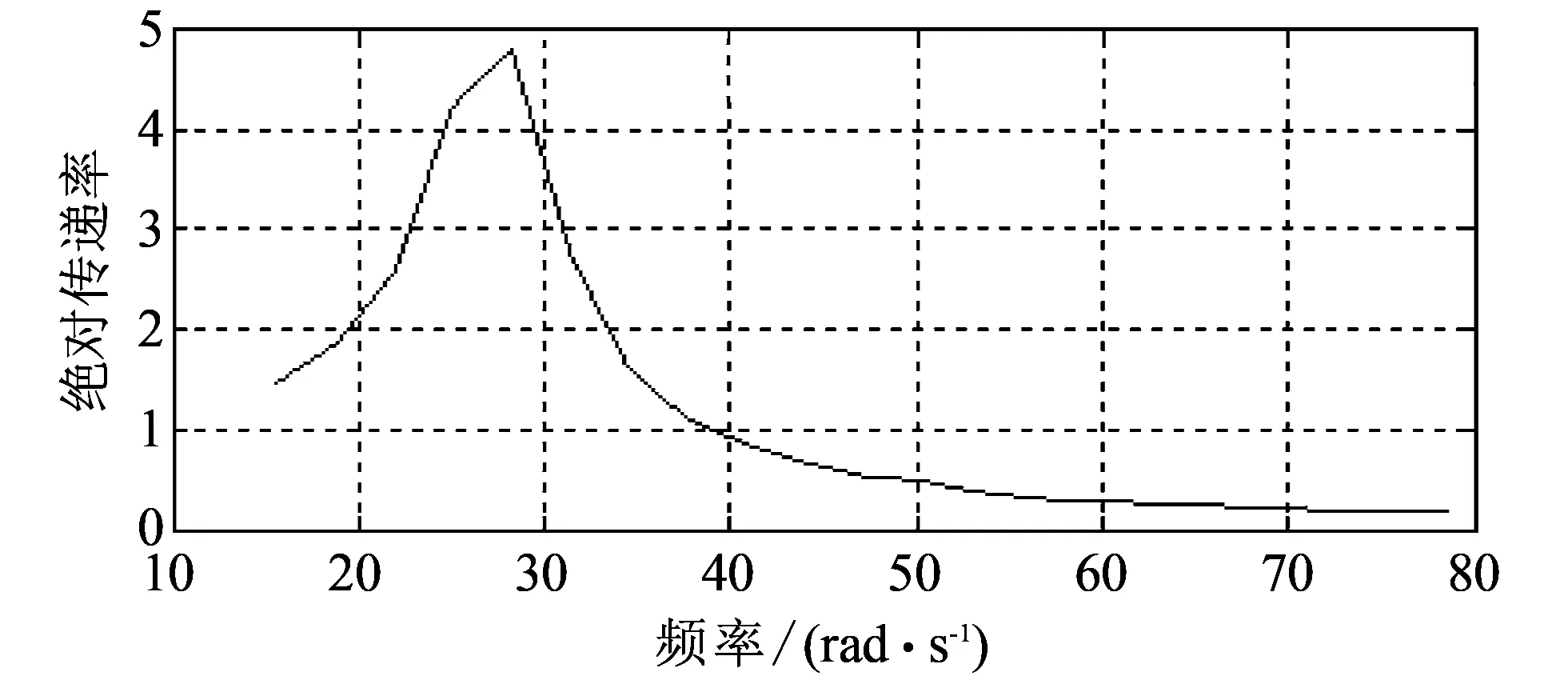
图 6 橡胶弹簧绝对传递率随激励频率的变化规律Fig.6 Absolute transmissibility changing rule of rubber spring following excitation frequency

4.2 质量对隔振特性的影响规律

为了研究橡胶弹簧隔振特性随系统质量的变化规律， 保持激励条件、 刚度、 阻尼不变， 得到不同质量下橡胶弹簧的绝对传递率如表 2 所示.

表 2 不同质量下橡胶弹簧的绝对传递率

橡胶弹簧绝对传递率随质量的变化规律如图 7 所示.

图 7 橡胶弹簧绝对传递率随质量的变化规律Fig.7 Absolute transmissibility changing rule of rubber spring following quality

4.3 刚度对隔振特性的影响规律

为了研究橡胶弹簧隔振特性随刚度的变化规律， 保持激励条件、 质量、 阻尼不变， 得到不同刚度下的橡胶弹簧绝对传递率如表 3 所示.

表 3 不同刚度下橡胶弹簧的绝对传递率

橡胶弹簧绝对传递率随刚度的的变化规律如图 8 所示.

图 8 橡胶弹簧绝对传递率随刚度的变化规律Fig.8 Absolute transmissibility changing rule of rubber spring following stiffness

4.4 阻尼对隔振特性的影响规律

为了研究橡胶弹簧隔振特性随阻尼的变化规律， 保持激励条件、 质量、 刚度不变， 得到不同阻尼下的橡胶弹簧绝对传递率如表 4 所示.

表 4 不同阻尼下橡胶弹簧的绝对传递率

橡胶弹簧绝对传递率随阻尼的变化规律如图 9 所示.

图 9 橡胶弹簧绝对传递率随阻尼的变化规律Fig.9 Absolute transmissibility changing rule of rubber spring following damping

由以上分析可知， 橡胶弹簧的绝对传递率随橡胶弹簧的刚度增加而增大； 随橡胶弹簧的阻尼增加而增大； 随橡胶弹簧隔振系统的质量增大而减小； 随激励频率的变化较复杂， 当激励频率小于28.3 rad/s时， 绝对传递率随着激励频率的增加而增大， 当激励频率为28.3 rad/s时， 绝对传递率最大， 而当激励频率大于28.3 rad/s时， 绝对传递率随着激励频率的增大而减小.

5 结 论

本文研究了橡胶弹簧的本构模型， 构建了橡胶弹簧隔振特性的理论模型， 测试了橡胶材料的力学特性， 建立了橡胶弹簧隔振系统的仿真模型， 进行了橡胶弹簧隔振特性的仿真计算， 探讨了橡胶弹簧隔振特性随激励条件、 橡胶弹簧隔振系统质量、 橡胶刚度、 阻尼的变化规律， 为橡胶弹簧隔振系统的设计开发提供了理论指导和技术支撑.

参考文献：

[1] Schmidt A, Gaul A. Finite element formulation of visco-elastic constitutive equations using fractional time derivatives[J]. Nonlinear Dynamics, 2002, 29(1-4)： 37-55.

[2] Karlsson F, Persson A. Modelling non-linear dynamics of rubber bushings-parameter identification and validation[D]. Skaner: Lund University, 2003.

[3] Sasso M, Palmieria G, Chiappinia G, et al. Characterization of hyperelastic rubber-like materials by biaxial and uniaxial stretching tests based on optical methods[J]. Polymer Testing, 2008, 27(8): 995-1004.

[4] Ho C, Langn Z Q, Billings S A. Design of vibration isolators by exploiting the beneficial effects of stiffness and damping nonlinearities[J]. Journal of Sound and Vibration, 2014, 333(12): 2489-2504.

[5] Liu L, Tan K K, Guo Y， et al. Active vibration isolation based on model reference adaptive control[J]. International Journal of Systems Science, 2014, 45(2): 97-108.

[6] Platz R, Enss G C. Comparison of uncertainty in passive and active vibration isolation[J]. Model Validation and Uncertainty Quantification, 2015, 3: 15-25.

[7] Li S, Fang B, Yang T Z, et al. Dynamics of vibration isolation system obeying fractional differentiation[J]. Aircraft Engineering and Aerospace Technology, 2012, 84(2): 103-108.

[8] 黄雪涛, 顾亮, 吕唯唯. 轻型载货汽车减振技术分析及优化设计[J]. 振动·测试与诊断, 2013, 33(2): 315-318.

Huang Xuetao, Gu Liang, Lü Weiwei. Vibration reduction technology analysis and optimal design on light truck[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 315-318. (in Chinese)

[9] 胡振娴, 顾亮. 汽车前悬架橡胶连接件的变形量时域响应[J]. 北京理工大学学报, 2010, 30(6): 651-654.

Hu Zhenxian, Gu Liang. Time response of front-suspension mount deflection[J]. Transactions of Beijing Institute of Technology, 2010, 30(6): 651-654. (in Chinese)

[10] 高俊, 季宏丽, 裘进浩. 基于层叠式PVDF作动器的混合隔振器的设计与特性研究[J]. 振动与冲击, 2015, 34(9): 141-148.

Gao Jun， Ji Hongli， Qiu Jinhao. Design and characteristics analysis of hybrid isolator based on laminated PVDF actuator[J]. Journal of Vibration and Shock, 2015, 34(9): 141-148. (in Chinese)

[11] 李玉龙, 白鸿柏, 何忠波， 等. 金属橡胶非线性减振系统混沌特性研究[J]. 北京理工大学学报, 2016, 36(5): 491-497.

Li Yulong, Bai Hongbai, He Zhongbo, et al. Chaotic Response of metal rubber vibration nonlinear isolation system[J]. Transactions of Beijing Institute of Technology, 2016, 36(5): 491-497. (in Chinese)

[12] 李玉龙, 白鸿柏, 何忠波. 金属橡胶消极减振系统复杂响应特性研究[J]. 振动与冲击, 2016, 35(4): 87-92.

Li Yulong, Bai Hongbai, He Zhongbo. Complex response characteristics of a passive metal-rubber vibration isolation system[J]. Journal of Vibration and Shock, 2016, 35(4): 87-92. (in Chinese)

[13] 王小莉, 上官文斌, 曾祥坤， 等. 基于开裂能密度及裂纹扩展特性的橡胶隔振器疲劳特性预测[J]. 振动与冲击, 2016, 35(6): 70-74.

Wang Xiaoli, Shangguan Wenbin, Zeng Xiangkun, et al. A method to predict fatigue performances of rubber isolator based on the cracking energy density and the fatigue crack growth characteristic of rubber material[J]. Journal of Vibration and Shock, 2016, 35(6): 70-74. (in Chinese)

[14] 杨俊. 橡胶弹簧动态特性研究[D]. 成都： 西南交通大学, 2015.

[15] 杨俊, 池茂儒, 朱旻昊， 等. 轨道车辆用弹性橡胶垫非线性模型研究[J]. 振动工程学报, 2016, 29(2): 291-297.

Yang Jun, Chi Maoru, Zhu Minhao, et al. The non-linear constitutive model of elastic rubber mat for rail vehicles[J]. Journal of Vibration and Shock, 2016, 29(2): 291-297. (in Chinese)