地学环境变量支持的土壤全钾含量自适应曲面建模——以青海湖流域典型地区为例

王胜利, 刘 伟, 张连蓬, 赵卓文, 朱寿红

(江苏师范大学 地理测绘与城乡规划学院, 江苏 徐州 221116)

土壤全钾含量在植物体中有着重要作用，可以激活植物体中的酶，促进新陈代谢；还可以提高作物抗旱、抗病、抗寒和抗倒伏能力，进而提高产量[1-2]。我国钾肥资源匮乏，耕地中近30%土壤缺钾。在南方地区土壤全钾含量不足已成为限制农业可持续生产的主要因素之一。因此，研究土壤全钾含量的空间分布特征，不仅对扩大或平衡土壤有效养分库具有重要意义，还能为土地资源的可持续利用和区域生态的健康发展提供理论依据[3-5]。从20世纪70年代开始，国外学者如Laslett[6]，Gotway等[7]对土壤空间变异规律展开广泛的研究；国内学者如傅伯杰[3]、胡正义[4]、黄翀[5]等对土壤养分、土壤属性和土壤污染的空间变异进行研究，取得了大量的研究成果。青海湖流域作为典型的生态系统敏感区，对其土壤全钾含量进行研究对扭转该地区钾含量亏缺、探明钾素总量具有一定的现实意义[8-10]。

由于土壤属性空间异质性和空间变异的复杂性，究竟何种插值方法最优，学术界并没有一个统一的认识[11-20]。比如对于Kriging，IDW 和Spline 三种常用的插值方法，研究人员做了大量的试验比较，但结论并不一致。一部分研究成果表明Kriging的模拟效果好于IDW[11-12]和Spline[12]，而另一部分研究结论恰恰相反[10,15]。有时插值方法的精度优势也往往是相互混淆的[11-13]。如张文龙等[14]通过对文登市土壤有机质空间变异性进行研究，发现普通克里格法(OK)中的Tetraspherical模型在模拟土壤有机质空间分布特征时优势明显。谢云峰等[15]对土壤Cd污染的插值模型对比，认为OK中的Exponential模型同样适合评价土壤属性的分布特征。赵巧丽等[16]通过比较不同插值方法评价土壤全氮含量的模拟误差，得出径向基函数法(RBF)插值模型优于IDW和OK。文雯等[9]以黄土丘陵小流域为研究区，马静等[17]以会宁县为研究区，分别比较了OK，IDW和RBF三种插值模型在模拟土壤有机碳含量和土壤速效钾含量在空间分布上的差异，结果表明，OK优于另外两种插值方法。对比以上研究发现，目前对土壤属性曲面建模的研究主要集中在讨论单一全局插值模型的预测精度，且预测结果有较大不确定性，整体插值精度有待进一步提高。

此外，地学环境变量对土壤属性的空间分异也有较大影响。如Triantafilis等[21]应用土壤电导率数据作为辅助数据估计土壤盐分含量。Kuriakose等[22]采用坡度、高程、土地利用等来预测土壤厚度。朱阿兴等[23]通过建立土壤—环境推理模型，基于土壤—环境关系模型的土壤相似度模型和对该模型进行赋值的推理技术模拟土壤图。张海涛等[24-25]利用RK，OCK和GWRK模型对土壤有机质空间分布进行预测，取得较好的效果。刘高焕等[5,26]基于NDVI、河流距离和高程研究黄河三角洲地区的盐渍化，指出结合环境要素的插值模型模拟效果更好。以上研究表明，利用与土壤属性密切相关的辅助变量，均能有效提高插值精度；但这些模型本身也存在一些不足，如贝叶斯模型还需进一步融合软数据；GWR模型在环境变量数目不足时，难以建立合理的回归模型等[5]。

针对上述问题，本文选取青海湖流域复杂地貌类型区为研究对象。以土地利用类型、土壤类型、草地类型和地貌类型等环境变量为辅助信息，构造多个基插值模型；自适应的筛选各个基插值模型最优模拟区域，进行有效集成，构造一个地学环境变量支持的多模型集成插值曲面模型(ASM-SP)，模拟青海湖流域部分地区土壤全钾含量的空间分布。结果表明，ASM-SP不仅考虑了土壤全钾含量空间布局与环境变量之间的相关关系，并将得到的最优区域进行自适应筛选，能较好地解决复杂地貌类型区单一全局插值模型模拟精度不足的问题。

1 研究区概况与研究方法

1.1 典型区域自然概况

青海湖流域(36°15′—38°20′N，97°50′—101°20′E)处于冻土地带，流域内地貌复杂、四周环山、湖泊河流密布，土壤植被类型繁多。土壤全钾丰缺程度会影响到植被覆盖度、地上生物量和生物多样性，对农业和畜牧业的发展有着决定性影响[27]。研究区位于青海湖流域西南部，在地质构造运动和长期外营力的综合作用下形成了复杂多样的地形地貌特征，主要包括刚察、海晏和共和三个地区，除去青海湖，总面积约为2 100 km2，海拔高度从3 043～4 516 m，有大量的农牧业活动，包括高山、丘陵、台地和冲击平原等，属于典型的复杂地貌类型区。

1.2 样品采集与分析

根据已有研究基础和研究区地形复杂度，采用空间分层组合抽样方式进行采样[28-29]，完成样点布设与优化，以获取研究区土壤全钾空间变异的全局特征和局部细节特征。如对台地、冲击平原等地形复杂度较小地区，采用规则格网采样；对山地、丘陵等地形复杂度较高地区，采用选择性采样；对丘陵和平原之间的过度地带，采用组合采样。由青海省环境监测中心人员提供采样协助，于2013年9月收集了110个青海湖流域典型地区土壤表层(0—30 cm)样点数据，在采样站点，记录采样位置的土壤样品、海拔、土壤类型、地貌类型和土地利用类型等信息，每个站点在0—5 cm，5—15 cm，15—30 cm依次取样三次，将野外采集的土壤样本带回实验室后，每个样本经过风干、研磨和过2 mm筛的流程后再进入试验分析阶段，最后测定本次研究所使用的土壤全钾含量，取三次平均值作为记录样本值。

1.3 数据处理

在ArcGIS 10.2软件中通过GNSS 将野外分层采样点的经纬度坐标与青海湖流域的空间分布坐标相连接，将测得的数据导入青海湖流域的点位表中，分别添加到四种地学要素类型图中，得到研究区土地利用类型图、土壤类型图、草地类型图、地貌类型图(附图3)。本研究主要采用0—30 cm土层的土壤全钾含量值作为研究对象。通过对OK，RK，GWRK和OCK 4种空间插值方法与ASM-SP的预测精度对比分析，筛选适合复杂地貌类型区的最优曲面建模方法。

1.4 地学要素筛选

大量研究表明[5,9,18,26,30]，利用地学要素作为辅助信息可以有效提高土壤属性插值精度和制图效果。土壤全钾空间变异性驱动因子主要包括：气候、母质、地形地貌、土壤类型、土地利用类型、草地类型、施肥、土地管理措施等[2]。依据该理论，考虑到本次研究主要针对自然景观类型区，排除施肥和土地管理措施两个驱动因子；结合数据的可获得性和前人研究成果[5,18,30]，选取土地利用类型、土壤类型、草地类型、地貌类型和坡度5个地学要素作为辅助变量。

为了筛选对土壤全钾空间分布具有显著影响的地学要素，利用SPSS软件对土壤全钾含量与上述5个地学要素进行方差分析，选取具有显著特征的地学要素作为辅助环境变量，融合RK，GWRK，OCK和ASM-SP模型进行插值。表1的方差分析结果表明：在本研究区，坡度与土壤全钾的空间分异之间不存在较强的相关性，原因在于研究区的坡度多数小于8°；而由于研究区范围较大，且样本空间较小以及样本空间分布不均匀，导致破碎度较大的草地类型没有足够的土壤采样点。最终，坡度和草地类型被排除在外。所有地学环境数据集通过ArcGIS 10.2制作，并重新采样为30 m分辨率。

表1 不同地学要素类型之间土壤全钾的方差分析

注：*0.05显著水平；**0.01显著水平。

1.5 融合地学环境信息的自适应曲面建模方法

传统的土壤属性插值方法有OK[9,18]、RK[18,25]、OCK[24,26]和GWRK[24-25,27]，OK利用区域化变量的原始数据和变异函数的特点，确定实测值参数对预测值的加权值大小，再对预测值做出最优的线性无偏估计，但其基于二阶平稳假设且需获得准确的半方差函数使其难以准确地描述土壤全钾的空间变异[30]；RK和OCK综合考虑了影响全钾空间变异的多种环境因子，但由于研究区地学环境要素分布比较破碎，导致没有足够多的采样点来估计相对准确的半方差函数；GWRK是GWR方法的延伸，用GWR局部拟合替代RK的全局拟合后，再将采样点处的模拟残差进行OK插值，使得拟合效果更加准确[5]。对全钾含量进行半变异分析，得到插值时的各参数值和拟合模型，其中块金值较小，表明自身随机性误差引起的变异性不大；N/S比值小于30%，S/N+S比值接近于1，表明全钾含量具有较强的空间相关性，拟合的最优模型为指数模型[9]。

总体来说，OCK，RK及GWRK等虽然精度获得不同程度提升，但在空间变异规律的详尽程度方面仍有待深入研究，且其精度势必还需进一步提高。本文的ASM-SP法根据空间相关与变异理论，在结合影响土壤全钾空间分异的地学环境变量进行插值的基础上，进一步将不同插值结果的最优区域自适应筛选集成，从而更准确刻画土壤全钾随周围地学环境要素类型而改变的突变边界，同时自适应集成的策略也使模拟精度获得了进一步的提升。土壤全钾的预测值和与其密切相关的地学环境变量之间的关系可表示为：

S(xi,l,k,yj,l,k)=trend(Geox,y)+r(xi,l,k,yj,l,k)

(1)

式中：S(xi,l,k,yj,l,k)为第l种地学要素的第k种类型的土壤全钾采样点预测值，其中(xi,yj)为采样点坐标，i和j分别表示坐标的行列号；trend(Geox,y)是描述(xi,yj)处第l种地学要素的第k种类型S的趋势值，其中Geo(x,y)是描述(xi,yj)处与土壤全钾密切相关的地学环境信息；r(xi,l,k,yj,l,k)是描述(xi,yj)处S的第l种地学要素的第k种类型中第i行、第j列栅格点土壤全钾的残差值[30-34]。基于以上理论，ASM-SP的流程图见图1，模拟过程如下：

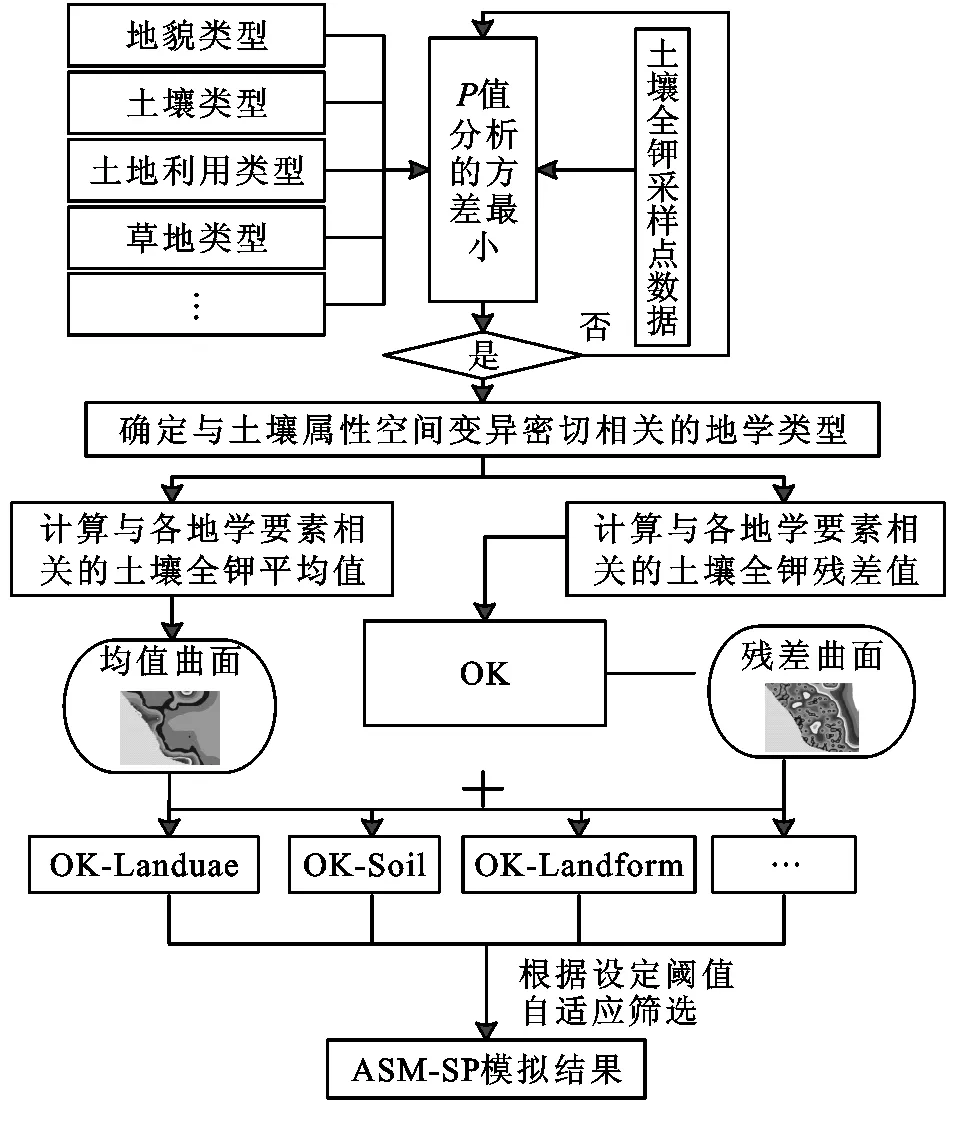
图1 ASM-SP方法的流程图

(1) 应用方差分析或线性混合模型等方法，分析哪些要素对土壤全钾的空间分异具有显著影响，并确定与土壤全钾空间分异密切相关的地学环境要素类别l；

(2) 依据采样点实测值，以及与土壤全钾空间分异密切相关的地学环境信息，利用多元回归或均值模型计算土壤全钾每种类型趋势以及每个土壤全钾采样点对应的残差值r(xi,l,k,yj,l,k)；

(3) 依据计算出的与各地学要素相关的土壤全钾趋势，得到研究区土壤全钾趋势面trend(Geox,y)；

(4) 依据采样点处的残差值，用OK模拟得到土壤全钾的残差曲面r(xi,l,k,yj,l,k)；

(5) 将趋势面和残差曲面相加得到与地学环境变量相关的土壤全钾插值曲面S(xi,l,k,yj,l,k)，由此构建OK-Landform，OK-Landuse，OK-Soil等一系列辅助地学环境变量的插值曲面模型Mi；

(6) 进行自适应筛选。首先利用Mi对整个研究区进行模拟得到模拟曲面，用采样点土壤全钾实测值减去预测值得到模拟误差，根据获得的模拟误差，用OK等线性插值构建误差曲面Si，计算每个网格点上土壤全钾的模拟误差，判断误差ei是否满足|ei|<ε，如果满足，则标记该网格点为聚类点，其中ε为误差阈值。之后根据标记点的空间位置，将满足精度阈值要求的区域聚类，Ri1，Ri2，Rik等为Mi插值模型的聚类空间。最后用Ri1，Ri2，Rik等空间范围掩膜对应的Mi插值曲面得到携带真值的聚类空间Ri1s，Ri2s，Riks，经过集成和No Data区域的填充，得到ASM-SP模拟的空间分布图。

1.6 插值结果的精度检验

插值精度采用独立验证进行评价[30]。随机将110个采样点分为80个插值点和30个验证点；利用80个插值点对验证点值进行预测；对比验证点的预测值和实测值。根据预测值和实测值的拟合程度评价插值模型的优劣[6, 12, 30]。评价指标包括ME，MRE，RMSE，AC、相关系数、回归系数和决定系数，其中ME，MRE，RMSE和AC的数学公式如下[9,15]：

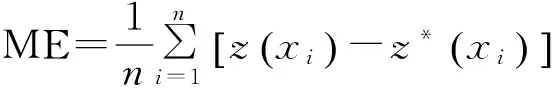
(2)

(3)

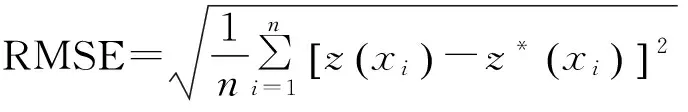
(4)

式中：z(xi)为土壤全钾含量的预测值；z*(xi)为土壤全钾含量的实测值；n为验证点的个数。

(5)

式中：PE为潜在误差变化(Potential error variance)；z*和z分别是实测值和预测值；o是实测值的均值。AC的取值范围从0到1，值越大表示预测结果越好；ME和RMSE的值越小，插值误差越小，精度越高；MRE可以克服量纲的影响，MRE越小，精度越高[15]。

2 模拟结果与分析

2.1 土壤全钾含量的统计特征

从研究区110个表层土壤全钾含量的统计结果分析可以看出(图2)，土壤全钾含量的值介于1.4065%～2.3464%之间，平均值为1.9588%，K-S检验结果表明全钾含量总体上服从正态分布。土壤全钾含量的变异系数为10.99%，表明研究区土壤全钾含量的空间变异度处在中等水平[15]。

2.2 精度分析

为了评价ASM-SP模拟土壤全钾含量空间分布的精度，本文比较了OK，RK，GWRK，OCK和ASM-SP5种插值方法的模拟效果(表2)。发现RK，GWRK，OCK和ASM-SP模拟的土壤全钾含量的ME比未结合地学信息插值方法(OK)的模拟效果更接近于0，说明采用结合地学信息插值方法的模拟结果有较好的无偏性。从MRE来看，ASM-SP最小，为89.69%，较OK，RK，GWRK和OCK分别降低7.05%，4.33%，3.24%和6.18%。类似地，RK，GWRK，OCK和ASM-SP的RMSE都要明显小于OK，其中ASM-SP的RMSE最小，为0.058 6，较OK，RK，GWRK和OCK分别降低45.07%，41.57%，20.81%和26.93%。ASM-SP的AC、回归系数和相关系数分别达到0.990 3，1.023，0.960 8，表明其回归曲线可以较好的模拟预测值与实测值的关系，插值效果优于其他插值方法；虽然OCK的回归系数大于GWRK，但其较低的相关系数和决定系数表明其预测效果逊色于GWRK，见图3。

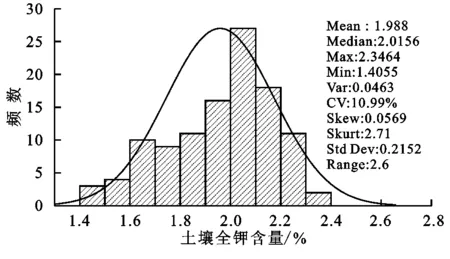
图2 全部样点的土壤全钾含量的描述统计和

总的来说，ASM-SP的模拟精度较高，原因在于它在插值过程中考虑了地学要素与土壤全钾之间的相关性，更能准确地刻画土壤全钾随地学环境要素变化而突变的边界；其次，将得到的最优区域进行自适应曲面建模，可以较好地提高研究区土壤全钾空间变异的预测精度。OCK插值效果提高原因在于其利用变量本身的空间自相关和协同变量协同相关进行预测，在一定程度上提高了精度，但是OCK仅依赖于变量自身的分布趋势，忽略了外界环境要素的影响；RK和GWRK更加重视地学环境要素的影响，其插值效果依赖于环境要素显得更加准确合理，但并没有对插值结果进行更进一步的自适应筛选，模拟精度逊色于ASM-SP。

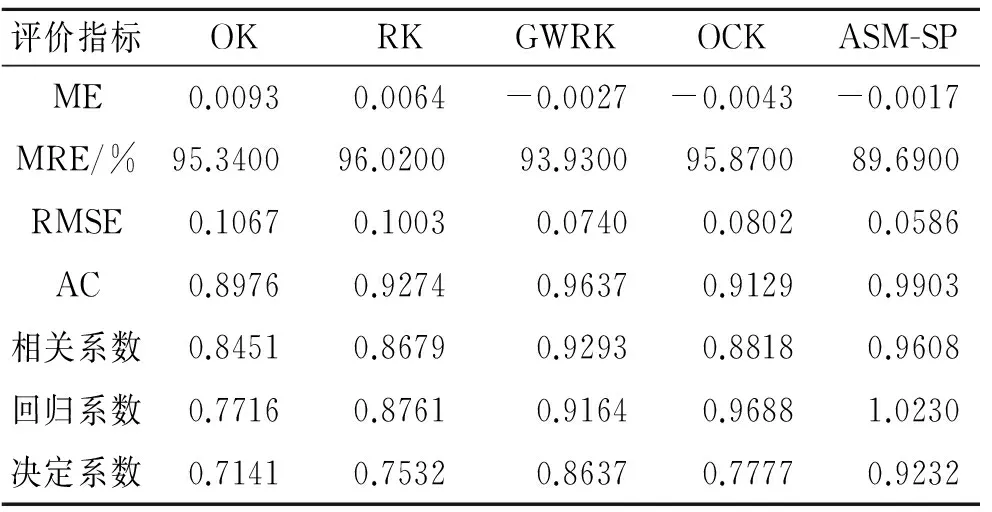
表2 OK，RK，GWRK，OCK和ASM-SP之间的精度对比

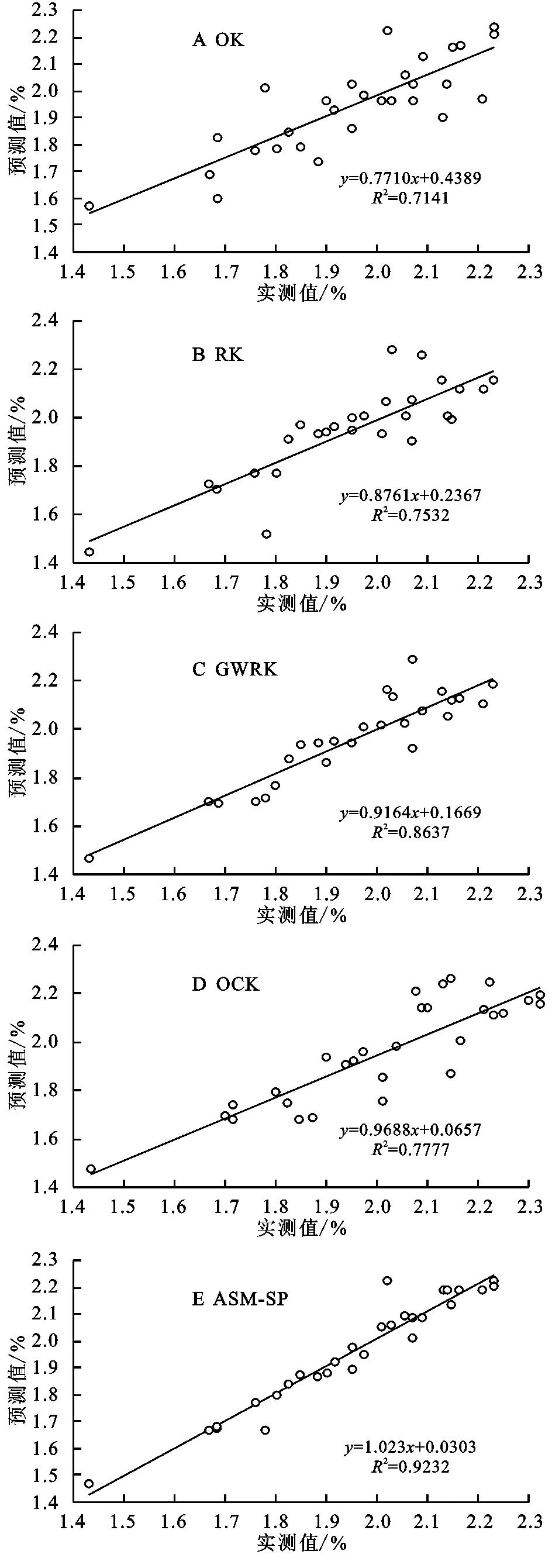
图3 研究区土壤全钾含量实测值与预测值模拟曲线

2.3 不同方法预测效果对比

为了得到5种插值方法的模拟效果，本文对比了OK，RK，GWRK，OCK和ASM-SP土壤全钾含量的插值效果图(图4)。

可以看出，OK和OCK的模拟曲面较为平滑，难以准确描述土壤全钾的局部变化信息，具有弱“牛眼”效应，其中OK的插值范围在这5种插值方法中最小(1.41～2.35)，原因为克里金插值的平滑效应，使刻画的变异程度较真实值小，此结论和多数的研究结果类似[15-22]；RK为全局性的插值方法，所有的插值点被用来计算模型的回归系数，且回归系数在插值过程中保持不变，如RK模型中土地利用类型的系数0.827是唯一的；而GWRK为局部性的插值方法，利用插值点周围有限个样点来计算该点的回归系数，逐步获取每个插值点的环境要素系数，利用OK对随机性残差插值使其更能揭示因空间非平稳性所掩盖的局部变化，本研究区中GWRK模拟精度优于RK，但如何更加重视变量在空间上的自相关和变量间的协同相关还需深入研究；ASM-SP在刻画研究区的空间变异性方面效果最好，其插值范围适中(1.26～2.44)，模拟结果更适应研究区复杂地貌状况，原因在于其不仅引入地学要素作为插值辅助变量，成功消除了OK的平滑效应，凸显了各地学要素边界处土壤全钾空间变异情景；而且，将得到的最优区域进行自适应筛选，进一步提高了预测精度；这些改进较好地适应了研究区复杂地貌类型。

图4 不同方法的土壤空间插值图对比

3 结 论

土壤属性空间变异较大，尤其在丘陵沟壑等复杂地貌区和不同地学要素衔接区会产生较大突变，因此有必要辅助环境变量对插值结果进行适当修正。此外，土壤属性的空间分异可能在很短水平距离内产生较大的变化，导致单一的全局插值模型在应用中常常会受到一定条件的限制。因此，通过融合地学环境要素的方法，将不同插值模型最优区域进行自适应建模可以较好地提高土壤属性预测精度，并便于预测结果的物理解释。

对比融合地学环境变量的空间插值模型(如RK，GWRK和OCK)，以及未使用辅助变量的空间插值模型(如OK)，结果显示，融合地学环境要素可以有效提高土壤全钾空间插值精度。将ASM-SP的模拟结果与其他插值方法(OK，RK，GWRK，OCK)的结果对比，发现ASM-SP刻画土壤全钾含量更加符合研究区土壤属性空间变异规律，地学要素边缘的细节信息突变表现的更加明显，ME，MRE和RMSE等精度评价指标也最小，预测值与实测值的AC、相关系数、回归系数和决定系数分别为0.990 3，0.960 8，1.023，0.923 2，显示出比其他插值模型更高的模拟精度，尤其能准确刻画研究区土壤全钾空间分异随周围地学环境要素变化而突变的边界，是适宜复杂地貌类型区土壤属性曲面建模的一种新方法，为以后的土壤属性制图研究提供了新思路和有益借鉴。

参考文献：

[1] 赵其国.土壤科学发展的战略思考[J].土壤,2009,41(5):681-688.

[2] 黄文忠.宜宾市土壤钾素的空间变异特征及影响因素研究[D].四川雅安:四川农业大学,2010.

[3] 郭旭东,傅伯杰,马克明.基于GIS和地统计学的土壤养分空间变异特征研究[J].应用生态学报,2000,11(4):557-563.

[4] 王彩绒,吕家珑,胡正义,等.太湖流域典型蔬菜地土壤氮磷钾养分空间变异性及分布规律[J].中国农学通报,2005,21(8):238-242.

[5] 吴春生,黄翀,刘高焕,等.黄河三角洲土壤含盐量空间预测方法研究[J].资源科学,2016,38(4):704-713.

[6] Laslett G M, McBratney A B, Pahl P J, et al. Comparison of several spatial prediction methods for soil pH[J]. European Journal of Soil Science, 1987, 38(2):325-341.

[7] Gotway C A, Ferguson R B, Hergert G W, et al. Comparison of kriging and inverse-distance methods for mapping soil parameters[J]. Soil Science Society of America Journal, 1996, 60(4):1237-1247.

[8] 龙军,张黎明,沈金泉,等.复杂地貌类型区耕地土壤有机质空间插值方法研究[J].土壤学报,2014,51(6):1270-1281.

[9] 文雯,周宝同,汪亚峰,等.基于辅助环境变量的土壤有机碳空间插值:以黄土丘陵区小流域为例[J].生态学报,2013,33(19):6389-6397.

[10] 王坷,Bailey.土壤钾素空间变异性和空间插值方法的比较研究[J].植物营养与肥料学报,2000,6(3):318-322.

[11] 马成霞,丁建丽,王璐,等.绿洲土壤表层含盐量空间变异分析的插值方法研究[J].水土保持研究,2014,21(4):317-320.

[12] Panagopoulos T, Jesus J, Antunes M, et al. Analysis of spatial interpolation for optimising management of a salinized field cultivated with lettuce[J]. European Journal of Agronomy, 2006,24(1):1-10.

[13] 董志南,郑拴宁,赵会兵,等.基于空间插值的风场模拟方法比较分析[J].地球信息科学学报,2015,17(1):37-44.

[14] 张文龙,李玉环,姬祥.基于地统计学的耕层土壤有机质空间变异及不同插值模型的比较[J].中国农学通报,2011,27(6):256-260.

[15] 谢云峰,陈同斌,雷梅,等.空间插值模型对土壤Cd污染评价结果的影响[J].环境科学学报,2010,30(4):847-854.

[16] 赵巧丽,郑国清,冯晓,等.河南省安阳县三种土壤全氮含量空间插值方法的比较分析[J].土壤通报,2012,43(5):1162-1166.

[17] 马静,张仁陟,陈利.耕地地力评价中土壤养分的空间插值方法比较研究:以会宁县土壤速效钾为例[J].安徽农学通报,2011,17(17):91-93.

[18] 史文娇,刘纪远,杜正平,等.基于地学信息的土壤属性高精度曲面建模[J].地理学报,2011,66(11):1574-1581.

[19] 刘劲松,陈辉,杨彬云,等.河北省年均降水量插值方法比较[J].生态学报,2009,29(7):3493-3500.

[20] 林琳,李纯厚,戴明,等.海洋浮游植物丰度的空间插值优化[J].生态学报,2007,27(7):2880-2888.

[21] Triantafilis J, Odeh I O A, Mcbratney A B. Five Geostatistical Models to Predict Soil Salinity From Electromagnetic Induction Data Across Irrigated Cotton[J]. Soil Science Society of America Journal, 2001,65(3):869-878.

[22] Kuriakose S L, Devkota S, Rossiter D G, et al. Prediction of soil depth using environmental variables in an anthropogenic landscape： A case study in the Western Ghats of Kerala, India[J]. Catena, 2009,79(1):27-38.

[23] 杨琳,朱阿兴,秦承志,等.运用模糊隶属度进行土壤属性制图的研究:以黑龙江鹤山农场研究区为例[J].土壤学报,2009,46(1):9-15.

[24] 郭龙,张海涛,陈家赢,等.基于协同克里格插值和地理加权回归模型的土壤属性空间预测比较[J].土壤学报,2012,49(5):1037-1042.

[25] 杨顺华,张海涛,郭龙,等.基于回归和地理加权回归Kriging的土壤有机质空间插值[J].应用生态学报,2015,26(6):1649-1656.

[26] 范晓梅,刘高焕,刘红光.基于Kriging和Cokriging方法的黄河三角洲土壤盐渍化评价[J].资源科学,2014,36(2):321-327.

[27] 易湘生,李国胜,尹衍雨,等.土壤厚度的空间插值方法比较:以青海三江源地区为例[J].地理研究,2012,31(10):1793-1805.

[28] 杨琳,朱阿兴,张淑杰,等.土壤制图中多等级代表性采样与分层随机采样的对比研究[J].土壤学报,2015,52(1):28-37.

[29] Zhang H, Lu L, Liu Y, et al. Spatial sampling strategies for the effect of interpolation accuracy[J]. ISPRS International Journal of Geo-Information, 2015,4(4):2742-2768.

[30] 史文娇,岳天祥,石晓丽,等.土壤连续属性空间插值方法及其精度的研究进展[J].自然资源学报,2012,27(1):163-175.

[31] 杨雨亭,尚松,浩李超.土壤水分空间插值的克里金平滑效应修正方法[J].水科学进展,2010,21(2):208-213.

[32] 王绍强,朱松丽,周成虎.中国土壤土层厚度的空间变异性特征[J].地理研究,2001,20(2):161-169.

[33] 范胜龙,黄炎和,林金石.表征土壤有机碳区域分布的优化空间插值模型研究:以福建省龙海市为例[J].水土保持研究,2011,18(6):1-5.

[34] Liu W, Du P, Zhao Z, et al. An adaptive weighting algorithm for interpolating the soil potassium content[J]. Scientific Reports, 2016,6:23889.