EQUI-ATTRACTION AND BACKWARD COMPACTNESS OF PULLBACK ATTRACTORS FOR POINT-DISSIPATIVE GINZBURG-LANDAU EQUATIONS∗

Yangrong LI(李荣)Lianbing SHE(佘连兵),2

1.School of Mathematics and Statistics,Southwest University,Chongqing 400715,China

2.Department of Mathematics,Liupanshui normal college,Liupanshui 553004,China

E-mail:liyr@swu.edu.cn;shelianbing@163.com

Jinyan YIN(尹金艳)

School of Mathematics and Information,China West Normal University,Nanchong 637002,China

E-mail:yjy111@email.swu.edu.cn

1 Introduction and Preliminaries

The central subject in in finitely dimensional dynamics is the long-time behavior of nonlinear evolution equations in realistic physical models.When the equation is autonomous,the asymptotic behavior can be described in terms of the so-called global attractor.The existence of a global attractor can be derived from “point dissipation plus asymptotic compactness”.A nice result can be founded in many references(see[1,2]).

Theorem 1.1A bounded semigroup has a global attractor if and only if it is point dissipative and asymptotically compact.

Caraballo et al[3]generalized Theorem 1.1 to establish the existence theorem of a pullback attractor for a point dissipative non-autonomous system.To explain their results,we need to recall some basic notations.

Let(X,d)be a metric space and B the collection of all bounded sets in X.An evolution process is a family of continuous mappings S(t,s):X→X(t≥s)satisfying S(s,s)=I and S(t,s)=S(t,r)S(r,s)for all t≥r≥s.

A non-autonomous set A(·)is a pullback attractor for a process S(·,·)if

(i)A(·)is compact,that is,every segment A(t)is compact in X for t∈ R;

(ii)it is invariant,that is,S(t,s)A(s)=A(t)for all t≥s;

(iii)it is pullback attracting,that is,dist(S(t,t− τ)D,A(t))=0 for D ∈ B;

(iv)it is the minimal one among all closed attracting sets.

RemarkThe condition(iv)is necessary to ensure the uniqueness.For example[4],both A1(t)=[−et,et]and A2(t)={0}are compact invariant attracting for the process S(t,s)x0=e−(t−s)x0on R.

Definition 1.2A process S(·,·)is strongly point dissipative if there is a bounded set B(·),which attracts points uniformly in the past:

Definition 1.3A process S(·,·)is strongly asymptotically compact if{S(sn,sn− τn)xn}is pre-compact whenever sn≤t with t∈R,τn→+∞ and{xn}is bounded.

If a process is autonomous,that is,S(t,s)=S(t−s,0)for all t≥ s,then,the strongly point dissipation is equivalent to the usual point dissipation,and the strongly asymptotic compactness is equivalent to the usual asymptotic compactness.

A process is said to be strongly bounded ifis bounded for each D∈B and t∈R.A process is equi-continuous if the family{S(s,s−τ):s≤ t}is equi-continuous at any x ∈ X,for all τ＞ 0,t∈ R.

For more details of pullback attractors,the readers can refer to the references(see two books[5,6]and many articles[7–13]).

Here,we only concern the following result given by Carvalho et al[5,Theorem 2.34].

Theorem 1.4Let S(·,·)be an equi-continuous and strongly bounded process,and assume that it is strongly point dissipative and strongly asymptotically compact.Then,it has a pullback attractor A(·)that is backward bounded,that is,is bounded for each t∈R.

One may regard Theorem 1.4 as a generalization of Theorem 1.1 from autonomous to the non-autonomous case.However,Theorem 1.4 is not completely satisfactory as it present only a sufficient condition rather than a necessary and sufficient criterion.

Our main purpose in this article is to strengthen as far as possible the conclusions in Theorem 1.4 from the following three aspects:

(1)Under the slightly weaker equi-continuity assumption than Theorem 1.4,we prove that the pullback attractor is backward compact,that is,is pre-compact for each t∈R.

The backward compactness of a pullback attractor seems to be involved firstly in[14]and developed by[4].In particular,the authors in[4]introduced a backward compact attractor,and established an existence theorem using the criteria of“bounded dissipation plus strongly asymptotically compactness”.

In this article,we will establish an existence theorem of a backward compact attractor from the point dissipation rather than the bounded dissipation.Note that the point dissipation is more convenient to verify in the realistic models.

(2)Under the same assumptions as given in Theorem 1.4,it is shown that the process has a so-called equi-attractor.

The equi-attractor is the main target of our study in this article,which is introduced in Section 2 and defined by the minimal one among all compact and(backward)equi-attracting sets.We will prove that equi-attraction implies the backward compactness of the corresponding pullback attractor.Therefore,the existence problem of an equi-attractor becomes the main problem in this article.In fact,in Section 3,we will prove that the same assumption in Theorem 1.4 is enough to ensure the existence of an equi-attractor.

(3)We can prove that the criterion in(2)is a necessary and sufficient condition for the existence of an equi-attractor.

Let a process satisfy some similar properties as equi-continuity.We can prove that the process has an equi-attractor if and only if it is strongly point dissipative and strongly asymptotically compact(see Theorem 3.5).This result is satisfactory because it completely parallels to the autonomous result given in Theorem 1.1.

Another purpose in this article is the application on the Ginzburg-Landau equation.This equation governs the finite amplitude evolution of instability waves.We will consider the evolution process of the instability wave when the equation is perturbed by some varying coefficients and a time-dependent external force.The backward temperedness of the force is assumed,and used to ensure that the asymptotic convergence of solutions is uniform backwards.Therefore,the above theoretical results can be applied to show the existence of both equi-attractor and backward compact attractor for the GL equation.

2 Equi-Attractors and Backward Compactness

Recall that a non-autonomous set B(·)is backward compact if both B(t)andare compact for each t∈ R.If B(·)is increasing,that is,B(s)⊂ B(t)for s ≤ t,then,backward compactness is equivalent to the(segmental)compactness.

A non-autonomous set A(·)is called a backward compact attractor for a process S(·,·)if it is backward compact,invariant,and attracting.By[4],this attractor must be the minimal one,and thus it is equivalent to a pullback attractor that is backward compact.

Now,we extend the concept of an attracting set.

Definition 2.1A non-autonomous set K(·)is said to be an equi-attracting set for a process S(·,·)if it attracts each bounded set uniformly in the past:

which is obviously equivalent toK(t))=0 from the definition of Hausdorffsemi-distance.

RemarkIn general,a pullback attractor(even its backward union)is not equi-attracting(see Example 2.8 later).So,the concept of equi-attracting sets is different from some uniformity of a pullback attractor given in[15].

2.1 Equi-attraction implies backward compactness

In this subsection,we prove an interesting result that the existence of a compact equiattracting set implies the existence of a backward compact attractor.This result is not trivial because we only require compactness(rather than backward compactness)of the equi-attracting set.

We need to introduce a terminology of a backward omega-limit set:

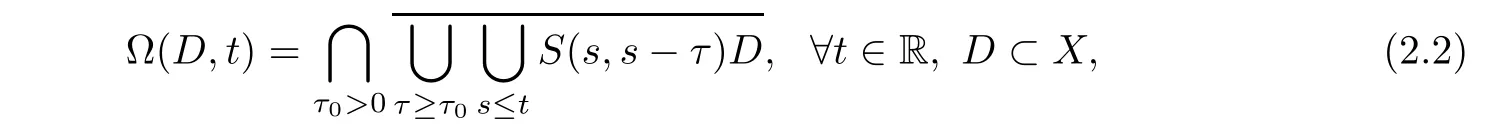
which generalizes the usual concept of a omega-limit set(see[5,6])

It is well-known that,for D⊂X and t∈R,

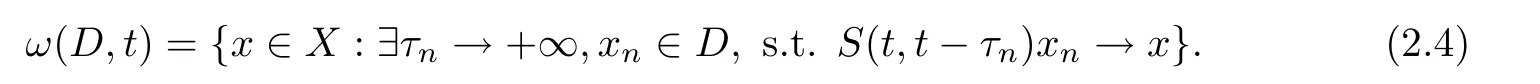
We provide a similar characterization for Ω(D,t)as the one for ω(D,t)in(2.4),and say more for the backward omega-limit set.

Lemma 2.2(i)y∈Ω(D,t)if and only if there are sn≤t,τn→+∞and xn∈D such that S(sn,sn−τn)xn→y.

(ii)For each D ⊂ X,the backward omega-limit set Ω(D,·)is increasing.

(iii)We have the following relationship:

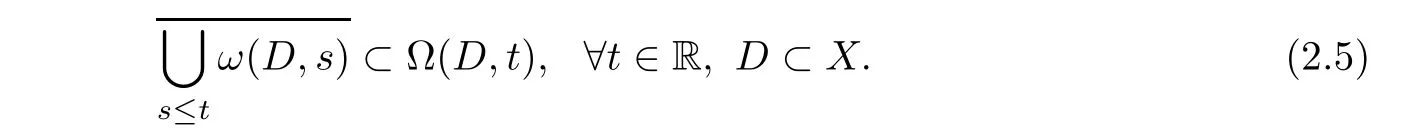
Proof(i)Let y∈Ω(D,t),then,by(2.2),

For each n∈N,we sequentially choose yn=S(sn,sn−τn)xnwith sn≤t,τn≥n,and xn∈D such that d(yn,y)≤1/n.Letting n→∞,it follows that S(sn,sn−τn)xn→y.

which proves y∈Ω(D,t).

(ii)If t1≤ t2,then,for each τ≥ 0 and D ⊂ X,

Hence,by(2.2),we have Ω(D,t1)⊂ Ω(D,t2),which proves the increasing assertion.

(iii)By(2.2)and(2.3),

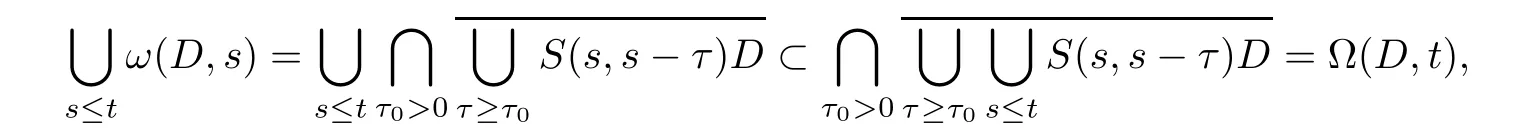
which implies(2.5)because of the closedness of Ω(D,t).

Theorem 2.3A process has a backward compact attractor A(·)if it has a compact equi-attracting set.

ProofSuppose that K(·)is a compact equi-attracting set(thus an attracting set)for a process S(·,·).By[5,Theorem 2.12],the process has a pullback attractor given by

It suffices to prove that A(·)is backward compact.For this end,let

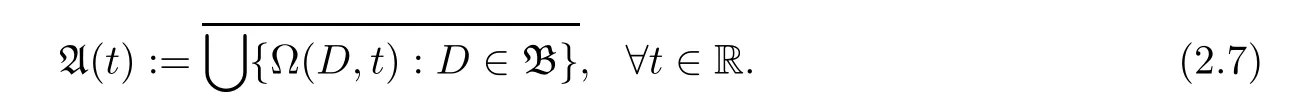
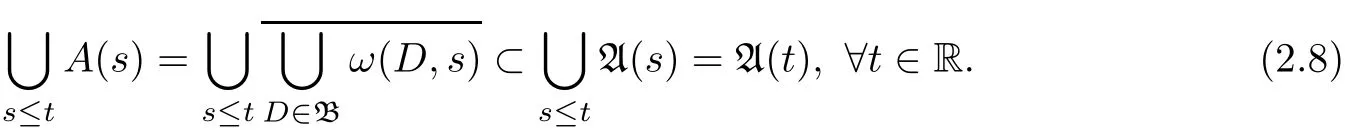
It suffices to prove the compactness of(t).Indeed,let D ∈B,t∈R,and x∈ Ω(D,t),then by Lemma 2.2(i),there are sn≤t,τn→∞and xn∈D such that S(sn,sn−τn)xn→x.By the equi-attraction of K(·)(see(2.1)),we know

So,d(x,K(t))=0,thus x∈ K(t),which implies Ω(D,t)⊂ K(t)for each D ∈ B.Hence,(t)⊂ K(t),so(t)is compact.Therefore,it follows from(2.8)that A(·)is backward compact as required.

Remark 2.4The converse problem of Theorem 2.3 remains open.We do not construct an example in which there is a backward compact attractor,but there does not exist any compact equi-attracting set.However,from Examples 2.8 and 3.8 later,one can find the difference between both attractors.

2.2 Equi-attractors

Motivated from the proof of Theorem 2.3,we introduce another attractor.

Definition 2.5A non-autonomous set(·)is an equi-attractor for a process if it is the minimal one among all compact equi-attracting sets.

In the above definition,the minimality means that(t)⊂ A(t),∀t∈ R,for any compact equi-attracting set A(·).An equi-attractor(if exists)has the following basic properties.Proposition 2.6If a process S(·,·)has an equi-attractor(·),then,

(d)there is a backward compact attractor A(·)such that

Proof(a)The uniqueness follows from the minimality given in Defination 2.5.

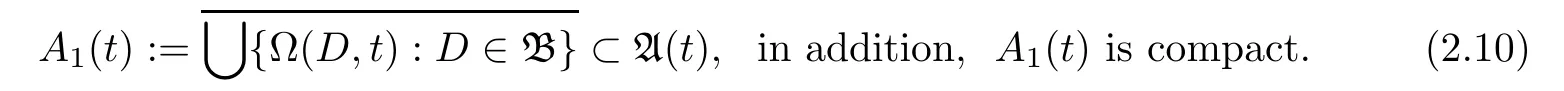
Conversely,we need to prove(t) ⊂ A1(t).For this end,we prove that A1(·)is an equiattracting set.By(2.1),this is equivalent to proving that,for each D∈B and t∈R,

If the above limit does not hold,then,there are δ＞ 0,τn→ ∞,t0∈ R,and D0∈ B such that

Hence,there exist sn≤t0and xn∈D0such that

By[5,Lemma 2.3]and the compactness of(t0),the sequence{S(sn,sn−τn)xn}has a convergent subsequence with the limit z.By Lemma 2.2,z∈Ω(D0,t0)⊂A1(t0),which contradicts with(2.11).Hence,A1(·)is equi-attracting,by(2.10),it is compact.Now,the minimality of(·)implies that(t)⊂ A1(t)as required.

(c)By Lemma 2.2, Ω(D,·)is increasing for each subset D ⊂ X.It follows that A1(·)given in(2.10)is also increasing and so is(·)from(b).In this case,which is compact.Therefore,(·)is backward compact.

This proves the first formulation in(2.9)because(t)is closed.

We then prove the second formulation in(2.9).Let t∈R be fixed.By(2.12),we know A(t− τ)⊂(t)for all τ≥ 0.By the invariance of A(·),we have

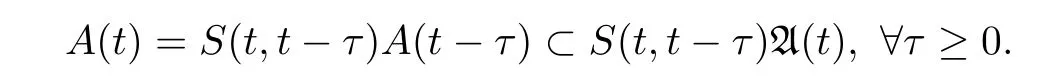
It follows from the closedness of A(·)that

On the other hand,it is obvious thatand so A(t)= ω((t),t).

The following proposition shows partial converse of the assertion(d)in Proposition 2.6,and provides a criterion to ensure that the inclusion in(2.9)becomes an equality.

Proposition 2.7(i)If a process S(·,·)has a backward compact attractor A(·),then,defines a compact and backward attracting set,which means that for each t∈R and B∈B,

The backward attraction is formally weaker than the(backward)equi-attraction.

(ii)If we further assume thatis equi-attracting,then,there exists an equi-attractor given by

(iii)If there is an equi-attractor(·)(so is a backward compact attractor A),then,the equality(2.13)holds true if and only ifis an equi-attracting set.

Proof(i)Let t∈R and B∈B be fixed.For each s≤t,it is obvious thatwhich implies that

By the equi-attraction of A1(·),we have,as τ→ ∞,

Next,we provide an example to show that the inclusion in(2.9)is strict andin Proposition 2.7 is not equi-attracting.

Example 2.8We consider a non-autonomous ODE on R:

with the initial condition x(s)=x0∈R,s≤0.It is easy to solve the first equation:

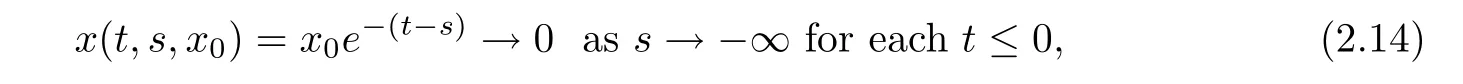
where the convergence is uniform in|x0|≤R.In particular,x(0,s,x0)→0 as s→−∞,which implies that

The second equation with the initial condition x(0)=x(0,s,x0)has the following solutions:

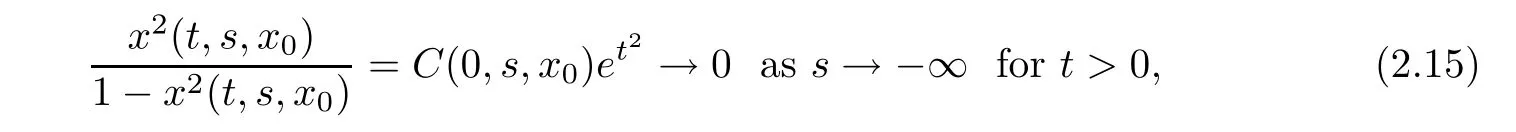
which further implies that x2(t,s,x0)→0 as s→−∞ for each t＞0.Hence,{0}is a compact pullback attracting set,and it is obviously minimal.So,the evolution process has a pullback attractor given by A(t)≡{0}.

On the other hand,it is easy from(2.14)–(2.15)to obtain

Let t＞ 0 and τ≥ t be fixed.We have

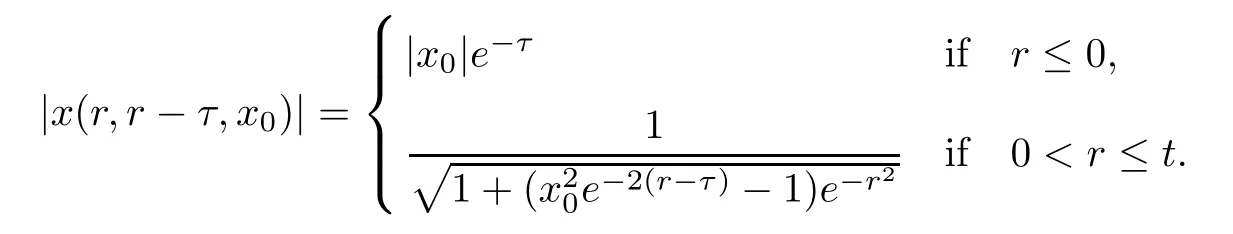
For any τ≥ t,we can choose r0∈ (0,t]and x0(small enough)such that

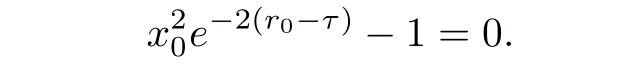
Hence,

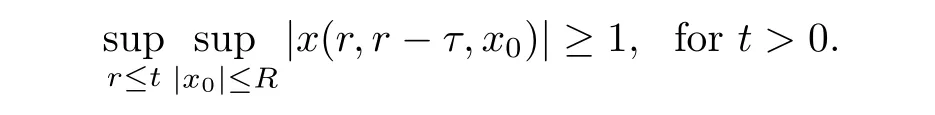
In fact,the above maximum equals to one if τ is large enough.Therefore,the set{0}(which is regarded as the backward union of A)is not an equi-attracting set.In contrast,by the following fact

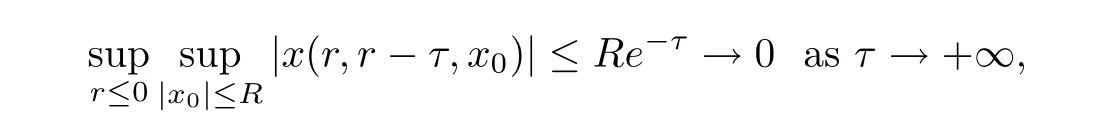
it is easy to prove that there is an equi-attractor given by

Therefore,the inclusion in(2.9)is strict.

2.3 Existence results from a compact attracting process

The following result extends Theorem 2.3,and tells us that the minimal one is available if the collection consisted of all compact equi-attracting sets is nonempty.

Theorem 2.9A process S(·,·)has an equi-attractor if and only if it has a compact equi-attracting set.

ProofNecessity.The equi-attractor itself is a compact equi-attracting set.

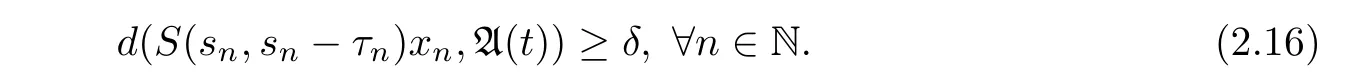
Assume that K(·)is a compact equi-attracting set,then it follows that

Passing to a subsequence,S(sn,sn−τn)xn→x for some x∈X.By Lemma 2.2,x∈Ω(D,t)⊂(t),which contradicts with(2.16).

Finally,we prove the minimality of(·).Let A(·)be another compact equi-attracting set.We need to prove Ω(D,t)⊂ A(t)for any D ∈B and t∈R.Let x∈ Ω(D,t).By Lemma 2.2,there are sn≤t,τn→∞,and xn∈D such that S(sn,sn−τn)xn→x.By the equi-attraction of A(·),as n → ∞,we have

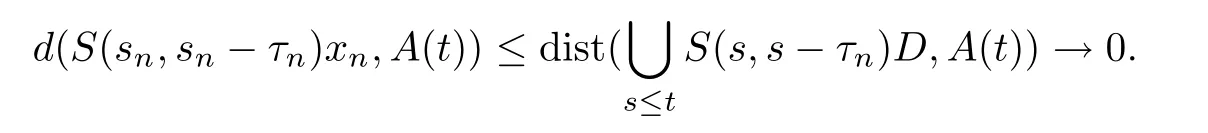
So,x ∈ A(t),which proves Ω(D,t)⊂ A(t)and thus(t)⊂ A(t).Therefore,(·)is indeed an equi-attractor in the sense of Defination 2.5.

2.4 Existence results from a bounded dissipative process

In[3,5],a process S(·,·)is called strongly bounded dissipative if it has a bounded and backward attracting set,where a backward attracting set K(·)means that it attracts every D∈B at any past time:

In this article,a process S(·,·)is called bounded equi-dissipative if it has a bounded equiattracting set.It is obvious that bounded equi-dissipation implies strongly bounded dissipation.In general,the converse is not true(see Example 2.8).

A set K(·)is an equi-absorbing set for a processes S(·,·)if,for each D ∈ B and t ∈ R,there exists a τ0= τ0(D,t) ＞ 0 such that

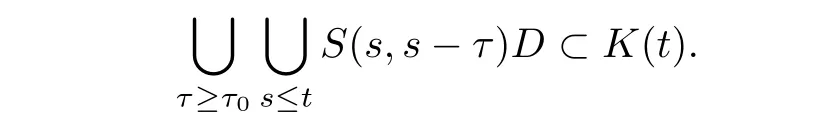
Lemma 2.10A process is bounded equi-dissipative if and only if the process has a bounded equi-absorbing set.

ProofEqui-absorption obviously implies equi-attraction.On the other hand,suppose that B(·)is a bounded equi-attracting set and let K(t)=N(B(t),1),the 1-neighborhood of B(t).Hence,the equi-attraction of B(·)implies the equi-absorption of K(·)immediately. □

Theorem 2.11A process S(·,·)has an equi-attractor(·)if and only if the process is bounded equi-dissipative and strongly asymptotically compact.In this case,(t)= Ω(K(t),t)for any bounded equi-absorbing set K(·).

ProofNecessity The equi-attractor itself is a bounded equi-attracting set;it follows that the process is bounded equi-dissipative.Let sn≤t with t∈R,τn→∞,and xn∈D with D∈B.By the equi-attraction again,we know that

SufficiencyBy Lemma 2.10,we can assume that K(·)is a bounded equi-absorbing set.Setting(t):= Ω(K(t),t)for each t∈ R,we will prove that(·)is an equi-attractor in the sense of Defination 2.5.

Indeed,let yn∈Ω(K(t),t)with n∈N.By Lemma 2.2,for each n∈N,we can choose sequentially τn＞ τn−1+1(ensuring τn→ ∞),sn≤ t,and xn∈ K(t)such that

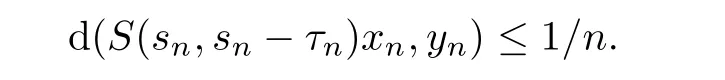
On the other hand,the strongly asymptotic compactness implies that{S(sn,sn−τn)xn}has a convergent subsequence,and so{yn}has also a convergent subsequence.Therefore,Ω(K(t),t)is compact.

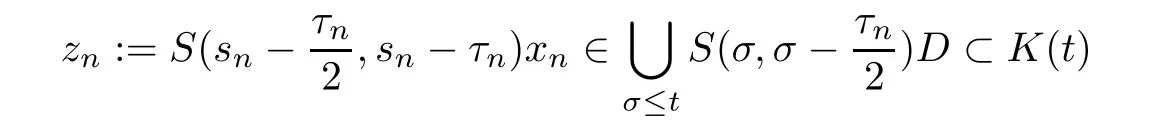
if n is large enough.In contrast,

It follows from Lemma 2.2 that y0∈Ω(K(t),t),which is a contradiction.

Finally,we prove the minimality.Let B(·)be another compact equi-attracting set and x∈ Ω(K(t),t)with t∈ R.By Lemma 2.2,there are τn→ ∞ andsuch that xn→ x.By the equi-attraction of B(·),and noting K(t)∈ B,we have

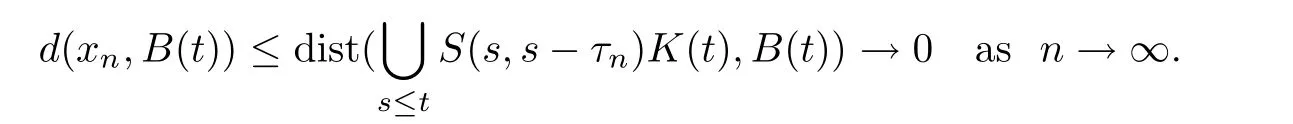
So,x ∈ B(t),and further Ω(K(t),t)⊂ B(t),which proves the minimality.

3 Existence Results From a Point Dissipative Process

3.1 Compact dissipative processes

A process is said to be strongly compact dissipative if there is a bounded set B(·)that equi-attracts every time-independent compact set C⊂X:

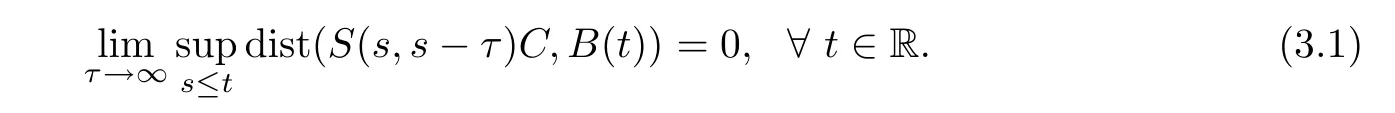
We now intend to strengthen[5,Theorem 2.33],in which the strongly bounded dissipation was derived from a strongly compact dissipative process.

Lemma 3.1Suppose that a process S(·,·)is strongly asymptotically compact.Then,it is bounded equi-dissipative if and only if it is strongly compact dissipative.

ProofThe necessity is obvious.To prove the sufficiency,we assume that a bounded set B(·)equi-attracts every compact set.Settingthe closed 1-neighborhood of B(t),we see that K(·)is bounded.We further prove that K(·)is an equi-attracting set by dividing into three steps.

Step 1K(·)equi-absorbs every compact set.Indeed,let C be a compact set and t∈ R.By(3.1),it is easy to prove that there is a τC＞ 0 such that

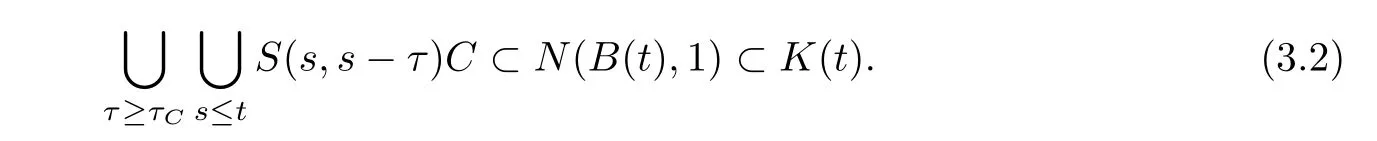
Step 2Ω(D,t)⊂K(t)for each D ∈B and t∈R.Indeed,let x∈ Ω(D,t),by Lemma 2.2,there are sn≤t,τn→∞,and xn∈D,such that S(sn,sn−τn)xn→x.Let now

Applying the strongly asymptotic compactness on(3.3),we know that{yn}has a convergent subsequence:

if k is large enough.Furthermore,the cycle property implies that

Step 3Ω(D,·)equi-attracts each D ∈ B.Indeed,let t∈ R be fixed,we need to prove

If(3.6)is not true,then there are δ＞0,sn≤t,τn→ ∞,and xn∈D such that d(S(sn,sn−τn)xn,Ω(D,t)) ≥ δ for each n ∈ N.By the strongly asymptotic compactness assumption,{S(sn,sn−τn)xn}has a convergent subsequence with a limit x∈Ω(D,t),which is a contraction.

In a word,by Step 2 and Step 3,K(·)equi-attracts every bounded set as required.

Applying Lemma 3.1 and Theorem 2.11,we have the following existence criterion of an equi-attractor.

Theorem 3.2A process has an equi-attractor if and only if the process is strongly compact dissipative and strongly asymptotically compact.

3.2 Point dissipative processes

A process S(·,·)is called strongly equi-continuous if,for each t ∈ R and x ∈ X,there is a τ0= τ0(x,t)such that the family{S(s,s− τ):s ≤ t,τ≥ τ0}of mappings is equi-continuous at x.This continuity may be stronger than the equi-continuity given in Theorem 1.4.However,we do not need the strong bounded assumption in the following result.

Lemma 3.3Suppose that a process S(·,·)is strongly equi-continuous.Then,it is strongly compact dissipative if and only if it is strongly point dissipative.

ProofIt suffices to prove that point dissipation implies compact dissipation.Let a bounded set B(·)equi-attracts every point.Let t∈ R be fixed.For each x ∈ X,it follows from the point-attraction of B(·)that there is a τ1(x) ＞ 0 such that

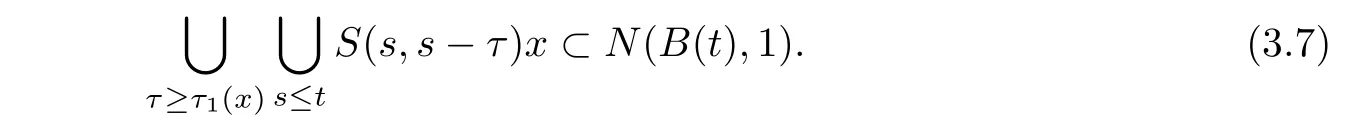
By the strongly equi-continuity,there is another τ(x) ＞ 0(with τ(x) ≥ τ1(x))such that{S(s,s− τ):s ≤ t,τ≥ τ(x)}is equi-continuous at x.Then,there further exists a δ(x)＞ 0 such that,whenever d(y,x)＜ δ(x),

which together with(3.7)implies that

for all s≤ t,τ≥ τ(x),and y∈ N(x,δ(x)).Therefore,

Let now C be a compact set in X.Hence,we can take{x1,x2,···,xm}such thatLet τC=max{τ(xi):i=1,2,···,m}.Then,by(3.8),

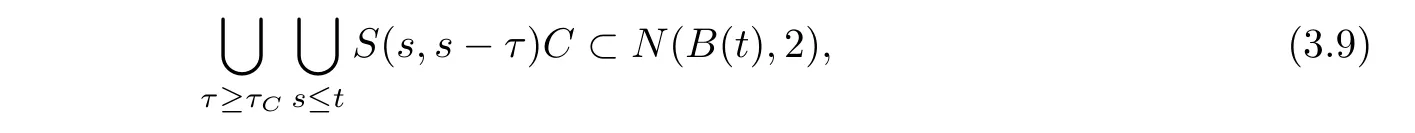
which proves that the bounded set N(B(·),2)equi-absorbs compact sets.Therefore,the process is strongly compact dissipative.

We now intend to reduce the strong equi-continuity assumption in Lemma 3.3.A process S(·,·)is called eventually equi-continuous if,for each t∈ R and x ∈ X,there is a τ0= τ0(x,t)such that,for each τ≥ τ0,the family{S(s,s− τ):s ≤ t}is equi-continuous at x.

The eventual equi-continuity is slightly weaker than the equi-continuity assumed in Theorem 1.4(in fact,the equi-continuity corresponds the case of τ0=0).

Lemma 3.4Suppose that a process S(·,·)is eventually equi-continuous and strongly bounded.Then,it is strongly compact dissipative if and that only if it is strongly point dissipative.

ProofSuppose that the process is strongly point dissipative.Fix t∈R and let B1(t)be bounded and equi-absorb each point.Then,for each x ∈ X,there is a τ0(x)such that

By the eventually equi-continuity,there is a τ(x)with τ(x) ≥ τ0(x),such that{S(s,s− τ(x)):s ≤ t}is equi-continuous at x,which together with(3.10)implies that there is a δ(x)＞ 0,such that ∪

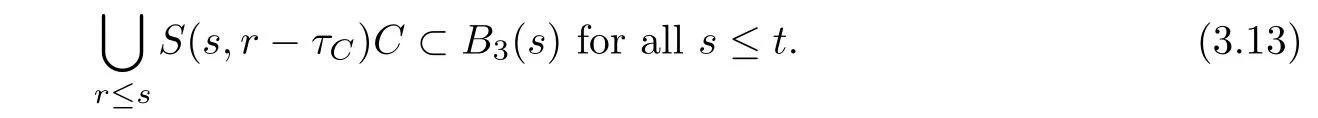
Indeed,if x∈C,then x∈N(xi,δ(xi))for some i.For each r≤s with s≤ t,it follows from(3.12)that

So,(3.13)holds true.By(3.13),we have

which means that K(t)equi-absorbs C and finishes the proof.

As an immediate consequence of Theorem 3.2,Lemma 3.3,Lemma 3.4,and Proposion 2.6,we have the final existence theorem of equi-attractors.

Theorem 3.5Suppose that S is either a strongly equi-continuous process or an eventually equi-continuous and strongly bounded process.Then,the process has an equi-attractorif and only if it is strongly point dissipative and strongly asymptotically compact.In this case,the process has also a pullback attractor A that is backward compact.Moreover,

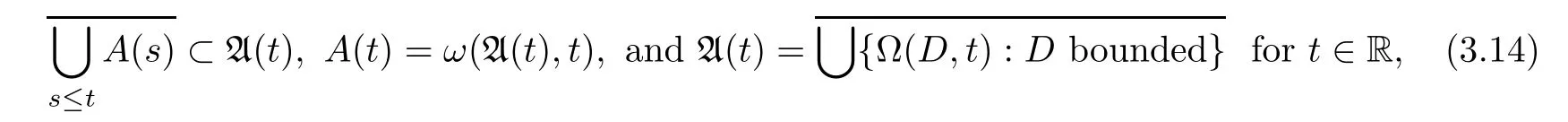
where the inclusion in(3.14)becomes an equality if and onlyis an equi-attracting set.In general,the inclusion is strict.

We remark here that the equi-attractor is different from the classical concept of a uniform attractor,which was introduced in[16]and developed by[17,18],etc.

Definition 3.6A deterministic set A is called a uniform attractor for a process S if it is the minimal one among all compact,globally equi-attracting sets,where the globally equiattraction means that for each B∈B,

Proposition 3.7A process S(·,·)has both backward compact attractor A(·)and backward equi-attractor(·)if it has a uniform attractor A.In this case,we have

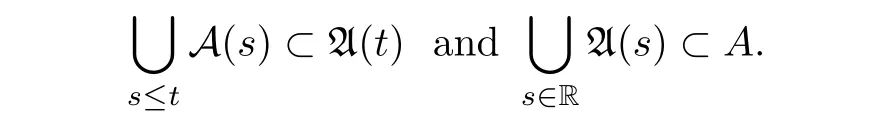
ProofIt is obvious that A(t)≡A is compact equi-attracting.By Theorem 2.9,there exists an equi-attractor(·).By the minimality of(·),it follows that(t) ⊂ A(t)=A for all t∈R.Other assertions on backward compact attractors follow from Proposition 2.6 immediately.

In the above proposition,we can not proveIn fact,the uniform attractor for the system in Example 2.8 is given by A=[−1,1],while the union of all components of the pullback attractor is{0}.However,we see from[19]that this equality holds true if the symbol space is compact.

In contrast,there are a large number of examples to show that there is an equi-attractor even if there does not exist a uniform attractor(see the next application section).Here,we give a simple example of ODE.

Example 3.8We consider˙x+x=f(t)with x(s)=x0.The explicit solution is given as follows:for∀t∈R,τ≥0,we have

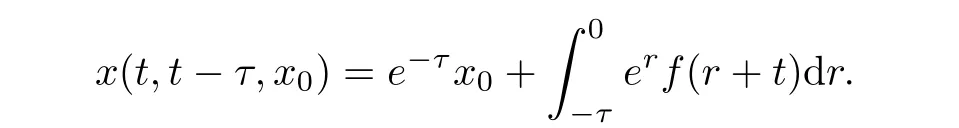
It is easy to see that the process has a pullback attractor consisted by a single orbit A(t)={x∗(t)}with

Let f(t)=et,then it is easy to calculate

For this example,we can prove that the backward unionis just an equi-attractor.Indeed,for any s≤ t with t∈ R and τ＞ 0,

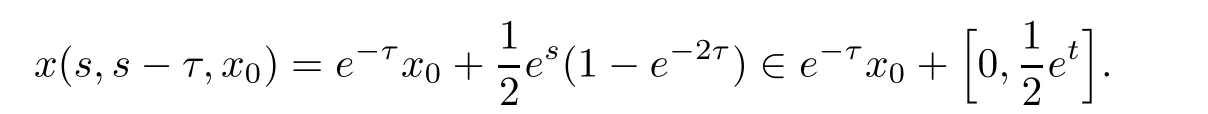
Therefore,as τ→ +∞,

In this example,we see that the equi-attractor is not an invariant set.Indeed,it is easy to calculate that

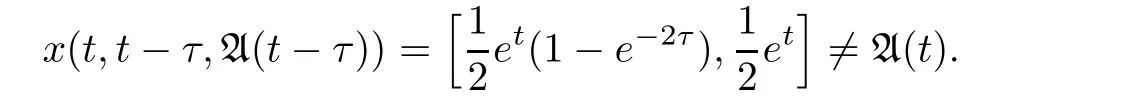
Remark 3.9(1)Comparing with Theorem 1.4,the conclusion in Theorem 3.5 is much stronger.However,the assumption of eventually equi-continuity is slightly weaker than the equi-continuity given in Theorem 1.4.

(2)We see from the above example that an equi-attractor is not invariant.This fact is similar as the case of uniform attractors,but unlike with the case of pullback attractors(cf.[20–22]).For uniform attractors,a similar problem as given in Remark 2.4 seems to remain open:Whether does there exist a uniform attractor if there is a globally compact pullback attractor?where the global compactness meansis pre-compact.

(3) It may be an interesting problem to study the regularity of an equi-attractor or a backward compact attractor.In[23–31],the usual attractor was proved to exist in a non-initial space for many stochastic PDEs.It is worth generalizing these results and establishing the regularity of an equi-attractor or a backward compact attractor in concrete non-autonomous models.We will discuss this subject in future papers.

4 Application on Non-Autonomous Ginzburg-Landau Equations

Let Ω be a bounded smooth domain in Rnwith n=1,2.The non-autonomous Ginzburg-Landau equation is read as

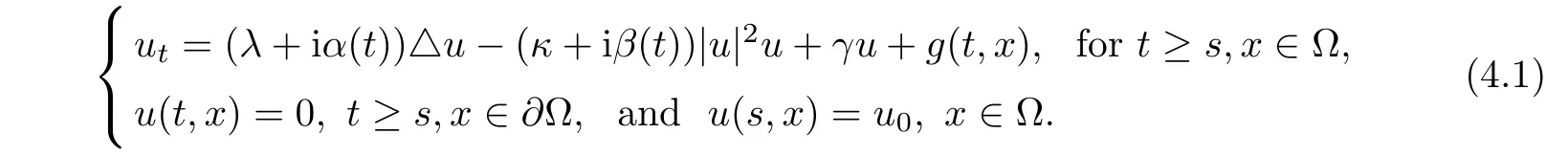
where the unknown u is a complex-valued function and λ,κ,γ ＞ 0.

If both α(·)and β(·)are constants,then a global attractor was obtained in[32]for g ≡ 0,and a random attractor was obtained in[33]if g is replaced by an additive noise.

Assume that α(·) ∈ C(R,R)and β(·) ∈ Cb(R,R),which are weaker than those given in[34](the authors assumed that α(·)∈ C(R,R)∩ L4(R)and

We also assume that the complex-valued forceand g is backward tempered:for the number γ given in Equation(4.1),

Setting H=L2(Ω)=L2(Ω)×L2(Ω)andone can prove that Equation(4.1)is well-posed,and the unique solution determines a process S(t,s):H→H by

We first prove that the process S is strongly point(compact,bounded)dissipative in H.Multiplying(4.1)by the conjugate¯u,integrating over Ω and taking the real part of the resulted equation,we obtain

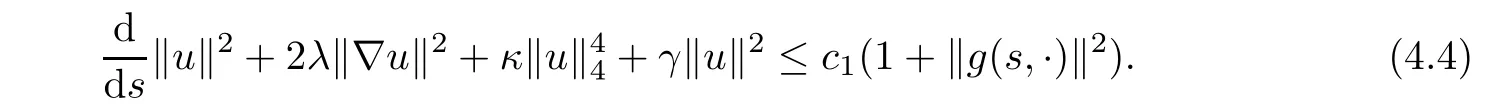
Let t∈R and u0∈H be fixed.Applying the Gronwall lemma on[s−τ,s],we have

Taking the supremum in s≤t,we know

where G(·)(given in(4.2))is finite and increasing.

Therefore,it follows from(4.6)that the process S is strongly point dissipative.In fact,the process is bounded equi-dissipative because

defines a bounded equi-absorbing set.In addition,by applying the Gronwall lemma on(4.4)again,we also obtain the following estimates:for all t∈R,τ≥0,and u0∈H,

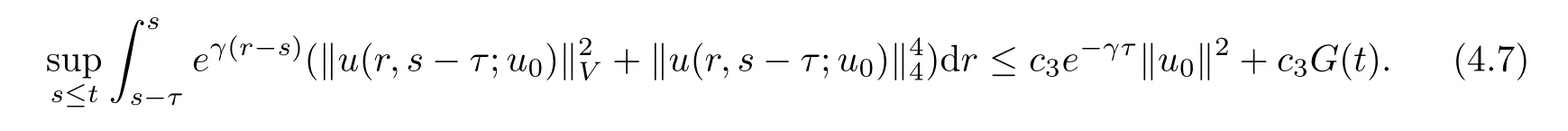
We now intend to prove that the process is strongly asymptotically compact.Multiplying(4.1)by−integrating over Ω,and taking the real part of the result,we obtain

The Young inequality implies that|(g(t,·),By the assumption β∈Cb(R,R),and settingwe obtain

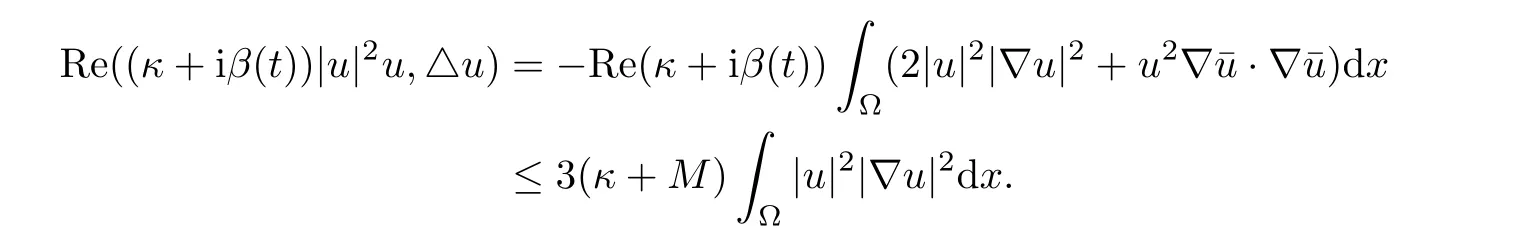
On the other hand,by the Sobolev embedding in Ω⊂Rnfor n=1,2,we have the following interpolation inequality:for ϕ ∈ V (cf.[32,(5.28)]).Therefore,

All above estimates deduce that

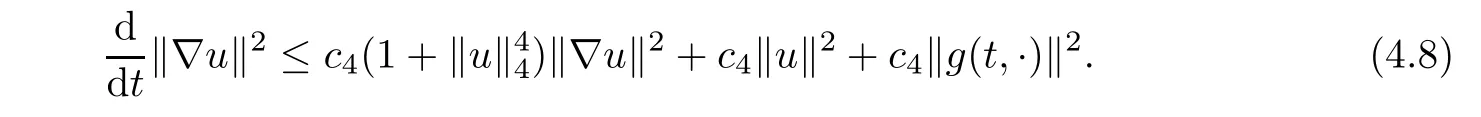
We need a non-autonomous form of the uniform Gronwall lemma(see[32,Lemma III 1.1]).

Lemma 4.1Let y,h1,h2be three positive locally integrable function and y′locally integrable on[s−τ,s],which satisfy

where τ＞0,s∈R.Suppose 0＜ σ ＜ τ,then we have

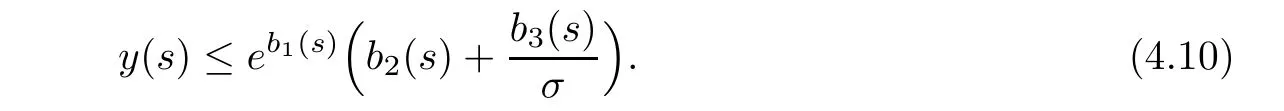
ProofWe multiply(4.9)byto obtain

Integrating the above inequality from r1=r2∈[s−σ,s]to r1=s,we find

Then,we obtain(4.10)by integrating the above inequality from r2=s−σ to r2=s.

Proposition 4.2The process given in(4.3)is strongly asymptotically compact in H.

ProofLet D be a bounded set in H with R=maxu0∈D‖u0‖ ＜ ∞,and let t∈ R befixed.We will apply Lemma 4.1 on(4.8)over the interval[s−τ,s]with s≤ t,τ＞ 2,and σ =1.From(4.7),there exists a τ0= τ0(R)≥ 2 such that,for all s≤ t,τ≥ τ0and u0∈ D,

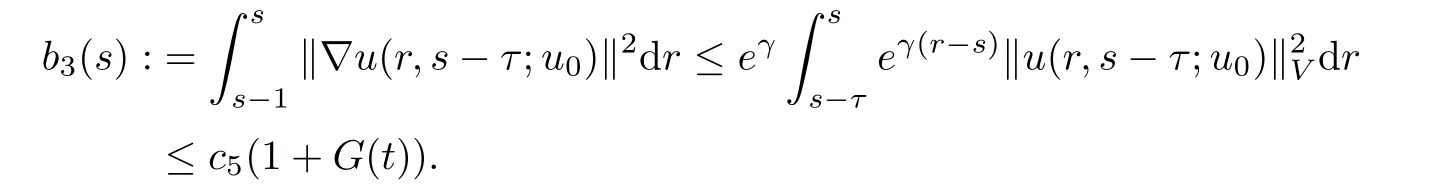
Similarly,

As G(·)is increasing,we know

Let sn≤ t,τn→ ∞,and u0,n∈D.Then,(4.11)implies that the sequence{S(sn,sn−τn)u0,n}is bounded in V,and thus pre-compact in H.Therefore,the process is strongly asymptotically compact in H.

By Theorem 2.11,3.2,3.5,and Proposition 4.2,we have the following application result.

Theorem 4.3Suppose that α∈C(R,R),β∈Cb(R,R),and g∈(R,H)is backward tempered in the sense of(4.2).Then,the process generated by the non-autonomous Ginzburg-Landau equation has an equi-attractorand a backward compact attractor A in H such that(3.14)holds true.

Remark 4.4(i)Note that we assume(4.2)only for the number γ given in Equation(4.1).In fact,we can prove that(4.2)holds true for arbitrary positive numbers,that is,

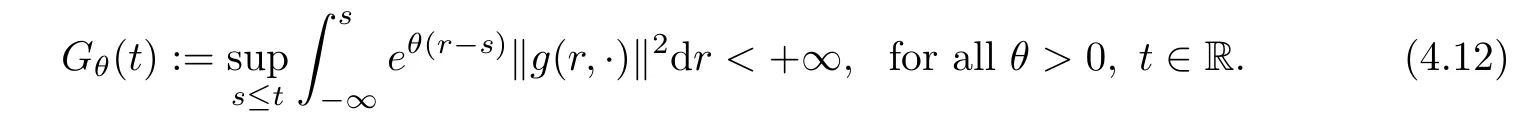
Indeed,let t∈R be fixed and let Gγ(t)＜ +∞,then we have

From(4.13),we also have,for each θ＞ 0,

(ii) In[4,14],g was called backward translation bounded if the first term in(4.13)is finite. From the above proof,we see that assumption(4.2)is equivalent to the backward translation boundedness,which is obviously weaker than the translation boundedness:The translation boundedness is the main assumption for the existence of a uniform attractor(see[16–18]).Therefore,there does not necessarily exist a uniform attractor if we only assume that g is backward tempered.

(iii)For the estimates in Proposition 4.2,we may need the higher regularity of the solution.The higher regularity can be obtained by the Galerkin method as done in Temma[32]and[35–38]for the autonomous GL equation.So,we have omitted the standard proof.

AcknowledgementsThe authors would like to thank Dr.Hongyong Cui for his suggestion on the counterexample 2.8.

[1]Hale J K.Asymtotic Behavior of Dissipative System.American Mathematical Society,1989

[2]Robinson J C.In finite-Dimensional Dynamical System.An Introduction to Dissipative Parabolic PDEs and the Theory of Global Attractors.Cambridge Text in Applied Mathematics,2001

[3]Caraballo T,Carvalho A N,Langa J A,Rivero F.Existence of pullback attractors for pullback asymptotically compact processes.Nonlinear Anal,2010,72:1967–1976

[4]Li Y,Wang R,Yin J.Backward compact attractors for non-autonomous Benjamin-Bona-Mahony equations on unbounded channels.Discrete Contin Dyn Syst B,2017,22:2569–2586

[5]Carvalho A N,Langa J A,Robinson J C.Attractor for In finite-dimensional Non-autonomous Dynamical Systems.Appl Math Sciences,182,Springer,2013

[6]Kloeden P E,Rasmussen M.Nonautonomous Dynamical Systems.American Mathematical Society,176,Providence,2011

[7]Bortolan M C,Carvalho A N,Langa J A.Structure of attractors for skew product semi flows.J Differ Equ,2014,257:490–522

[8]Park S H,Park J Y.Pullback attractor for a non-autonomous modified Swift-Hohenberg equation.Comput Math Appl,2014,67:542–548

[9]Guo B,Guo C,Pu X.Random attractors for a stochastic hydrodynamical equation in heisenberg paramagent.Acta Mathematica Scientia,2011,31B:529–540

[10]Zhao C,Li Y,Zhou S.Random attractor for a two-dimensional incompressible non-Newtonian fluid with multiplicative noise.Acta Mathematica Scientia,2011,31B:567–575

[11]Qin Y,Yang X,Liu X.Pullback attractors for the non-autonomous Benjamin-Bona-Mahony equations in H-2.Acta Mathematica Scientia,2012,32B:1338–1348

[12]Wang B.Sufficient and necessary criteria for existence of pullback attractors for non-compact random dynamical systems.J Differ Equ,2012,253:1544–1583

[13]Zvyagin V,Kondratyev S.Pullback attractors of the Jeffreys-Oldroyd equations.J Differ Equ,2016,260:5026–5042

[14]Cui H,Langa J A,Li Y.Regularity and structure of pullback attractors for reaction-diffusion type systems without uniqueness.Nonlinear Anal,2016,140:208–235

[15]Kloeden P E,Pötzsche C,Rasmussen M.Limitations of pullback attractors for processes.J Differ Equ Appl,2012,18:693–701

[16]Chepyzhov V V,Vishik M I.Attractors of non-autonomous dynamical systems and their dimensions.J Math Pures Appl,1994,7:279–333

[17]Wang Y,Zhou S.Kernel sections and uniform attractors of multi-valued semiprocesses.J Differ Equ,2007,232:573–622

[18]Sun C,Cao D,Duan J.Uniform attractors for nonautonomous wave equations with nonlinear damping.SIAM J Appl Dyn Syst,2007,6:293–318

[19]Cui H,Langa J A,Li Y,Valero J.Attractors for Multi-valued Non-autonomous Dynamical Systems:Relationship,Characterization and Robustness.Set-Valued Var Anal,online,2016.DOI:10.1007/s11228-016-0395-2

[20]Zelati M C,Kalita P.Minimality properties of set-valued processes and their pullback attractors.SIAM J Math Anal,2015,47:1530–1561

[21]Zelati M C.On the theory of global attractors and Lyapunov functionals.Set-Valued Var Anal,2013,21:127–149

[22]Chepyzhov V V,Conti M,Pata V.Totally dissipative dynamical processes and their uniform global attractors.Commun Pure Appl Anal,2014,13:1989–2004

[23]Cao D,Sun C,Yang M.Dynamics for a stochastic reaction-diffusion equation with additive noise.J Differ Equ,2015,259:838–872

[24]Gess B.Random attractors for stochastic porous media equations perturbed by space-time linear multiplicative noise.Annals Probability,2014,42:818–864

[25]Li Y,Cui H,Li J.Upper semi-continuity and regularity of random attractors on p-times integrable spaces and applications.Nonlinear Anal,2014,109:33–44

[26]Li Y,Gu A,Li J.Existence and continuity of bi-spatial random attractors and application to stochastic semilinear Laplacian equations.J Differ Equ,2015,258:504–534

[27]Li Y,Guo B.Random attractors for quasi-continuous random dynamical systems and applications to stochastic reaction-diffusion equations,J Differ Equ,2008,245:1775–1800

[28]Li Y,Yin J.A modified proof of pullback attractors in a Sobolev space for stochastic Fitzhugh-Nagumo equations.Discrete Contin Dyn Syst B,2016,21:1203–1223

[29]Lukaszewicz G.On pullback attractors in H10for nonautonomous reaction-diffusion equations.Intern J Bifur Chaos,2010,20:2637–2644

[30]Song H.Pullback attractors of non-autonomous reaction-diffusion equations in H10.J Differ Equ,2010,249:2357–2376

[31]Zhao W.Regularity of random attractors for a stochastic degenerate parabolic equations driven by multiplicative noise.Acta Mathematica Scientia,2016,36B:409–427

[32]Temam R.In finite-Dimensional Dynamical Systems in Mechanics and Physics.New York:Springer-Verlag,1997

[33]Wang G,Guo B,Li Y.The asymptotic behavior of the stochastic Ginzburg-Landou equation with additive noise.Appl Math Comput,2008,198:849–857

[34]Cui H,Li Y,Yin J.Existence and upper semicontinuity of bi-spatial pullback attractors for smoothing cocycles.Nonlinear Anal,2015,128:304–324

[35]Li B,Zhu H,Zhao C.Time decay rate of solutions to the hyperbolic MHD equations in R-3.Acta Mathematica Scientia,2016,36B:1369–1382

[36]Wang Y,Wang L.Trajectory attractors for nonclassical diffusion equations with fading memory.Acta Mathematica Scientia,2013,33B:721–737

[37]Zhang F,Guo B.Attractors for fully discrete finite difference scheme of dissipative Zakharov equations.Acta Mathematica Scientia,2012,32B:2431–2452

[38]Zhong Y,Sun C.Uniform quasi-differentiability of semigroup to nonlinear reaction-diffusion equations with supercritical exponent.Acta Mathematica Scientia,2017,37B:301–315