EXISTENCE AND BLOW-UP BEHAVIOR OF CONSTRAINED MINIMIZERS FOR SCHRÖDINGER-POISSON-SLATER SYSTEM∗

Xincai ZHU(朱新才)

1.Wuhan Institute of Physics and Mathematics,Chinese Academy of Sciences,Wuhan 430071,China

2.University of Chinese Academy of Sciences,Beijing 100049,China

E-mail:zhuxc68@163.com

1 Introduction

We consider the following nonlinear Schrödinger-Poisson-Slater(SPS)system

where p ∈ (2,6).V(x)denotes Coulomb potential of the system,and λ ∈ R describes the chemical potential.

System(1.1)can be obtained by looking for standing waves φ(x,t)=e−iλtu(x)of the following equation

which coincides with the Schrödinger-Poisson(SP)system when the contribution of the last term(the Slater term)is not considered;see,for example,[3,6,13,14,19]and the references therein.Whenwhich is known as the repulsive Coulomb potential,system(1.1)appears in various physical frameworks,such as plasma physics or semiconductor theory,and is studied extensively in recent years;see[1,10,11,19,23]for instance.As for the attractive Coulomb potentialsystem(1.1)is,however,related to some applications about the quantum gravity;see[18,19,22]and the references therein.

In this article,we study the attractive Coulomb potentialwhich corresponds to the phase of standing waves for the time-independent system(1.1).We investigate the following constrained minimization problem associated with system(1.1),

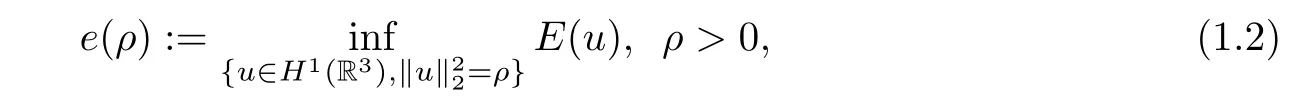
where E(u)is the energy functional satisfying

It is well known that the minimizers of(1.2)are prescribed L2-norm solutions of(1.1).Without loss of generality,we can restrict the minimizers of(1.2)to nonnegative functions,because of the fact that E(u)≥E(|u|)holds for any u∈H1(R3).

One of the main difficulties in solving problem(1.2)is that the Sobolev embedding H1(R3)→Lp(R3)for p ∈ [2,2∗)is not compact.The possible loss of the compactness due to that invariance has been detected by the techniques well-known as the concentration-compactness method;see[15,16,19].As another aspect,the existence of minimizers for(1.2)depends heavily on the exponent p.Especially,when p=,some other difficulty arises in studying problem(1.2),because the system may collapse if the single particle mass ρ of the system is large enough.Inspired by the recent works[7–9],when p=,it turns out that the critical mass ρ∗＞ 0 is well connected with the optimal coefficient of the Gagliardo-Nirenberg inequality in[20].More precisely,in this case,functional(1.2)has at least one minimizer if ρ ∈ (0,ρ∗),and there is no minimizer for ρ ≥ ρ∗.The critical valuewhere φ ＞ 0 denotes the unique(up to translations)positive radially symmetric solution of the following nonlinear scalar field equation

see,for example,[12,17].

Before going to discuss the existence results for(1.2),we first give the following Gagliardo-Nirenberg inequality(see Theorem A in[20]):

where Kpis a positive constant determined by the exponent p.Especially,if p=,thenand(1.5)is reduced as

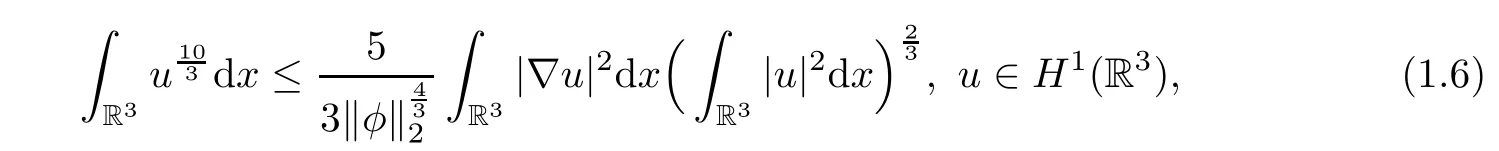
where the equality is achieved at u(x)= φ(x) ＞ 0 with φ(x)satisfying(1.4).We then deduce from(1.4)and(1.6)that

Moreover,by applying the Hardy-Littewood-Sobolev inequality(cf.[5]),it yields that

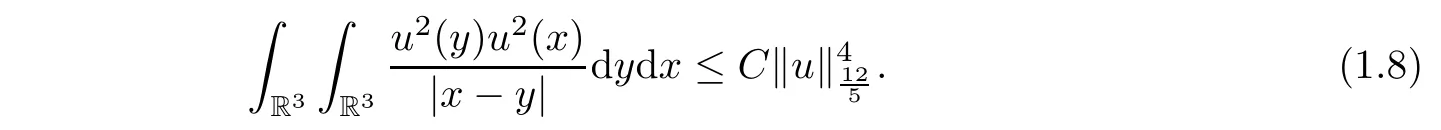
Here and below,the symbol C stands for positive constants.Similar to the proof of Lemma 1.2 in[5],by applying interpolation inequality and Sobolev imbedding inequality,we deduce that

Hence,the last two inequalities imply that

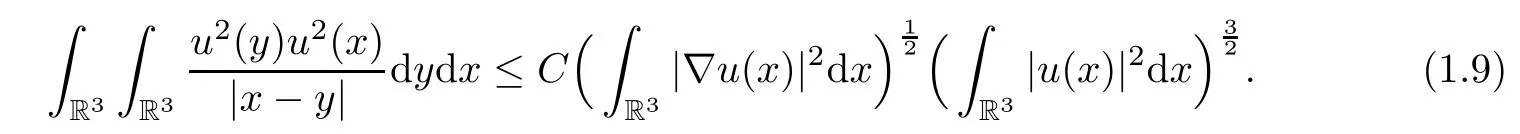
In view of the above facts,we next state the following existence and nonexistence of minimizers.

Theorem 1.1Let φ(x)be the unique(up to translations)positive radially symmetric solution of(1.4).Then,we have the followings:

(a)If 0 ＜ ρ ＜ ρ∗:=there exists at least one minimizer for e(ρ);

(b)If ρ ≥ ρ∗,there is no minimizer for e(ρ).

In Section 2,we shall address the proof of Theorem 1.1.Even though the proof of Theorem 1.1 is stimulated by[7–9],where different variational problems were studied,the methods used there are false in our situation because of the possible loss of the compactness.We shall overcome this difficulty by the concentration-compactness methods;see[15,16,19].Theorem 1.1 gives essentially the existence of nonnegative minimizers for e(ρ),which are actually positive by strong maximum principle.

Theorem 1.2For p=,let uρ(x)be a nonnegative minimizer of(1.2)for any ρ ∈(0, ρ∗).Then,for any sequence{ρk}with ρk↗ ρ∗as k → ∞,there exist a subsequence(still denoted by{ρk})of{ρk}and{y∈ρk} ⊂ R3,and y0∈ R3such that

where φ(x)is the unique positive(up to translations)radially symmetric solution of(1.4),and∈ρksatisfies

As proved in Section 3,Theorem 1.2 shows a detailed description of the mass concentration(that is,blow-up)behavior of minimizers as ρk↗ ρ∗for the case where p=.In fact,the blow-up rate of minimizers is obtained from a refined energy estimate of e(ρk)(see Lemma 3.2),where e(ρk)satisfies

2 Existence and Nonexistence of Minimizers

In this section,we complete the proof of Theorem 1.1.The existence part of Theorem 1.1 is inspired by[7–9],together with the concentration-compactness methods[15,16,19].We shall prove the nonexistence results of Theorem 1.1 by deriving the energy e(ρ)= −∞.

Proof of Theorem 1.1(1)We first consider two cases,where either 2＜p＜103,ρ ∈ (0,∞)orLet φ(x)be the unique positive solution of(1.4).Suppose that u=u(x)satisfiesApplying inequalities(1.5),(1.6)and(1.9),then we deduce that if 2＜p＜,ρ∈ (0,∞),

One can conclude from(2.1)and(2.2)that E(un)is bounded from below uniformly for any sequencewithIn fact,it is obvious whenis bounded.Whenas n→ ∞,one can check that E(un)≥ 0 as n→ ∞.Therefore,there exists a minimizing sequence{un}⊂ H1(R3)satisfyingandIt then follows from(2.1)and(2.2)that the minimizing sequence{un}is bounded uniformly in H1(R3).

In order to establish the existence of minimizers,we firstly need to prove that the minimizing sequence is compact.As the minimizing sequence{un}is bounded uniformly in H1(R3)withit follows from[15]or[16,Lemma III.1]that there exists a subsequence of{un},still denoted by{un},for which either the compactness or the dichotomy or the vanishing occurs in L2(R3).In fact,we can rule out the cases of the vanishing and the dichotomy as following claims.

Claim 1The minimizing subsequence{un}can not vanish.

On the contrary,suppose that the vanishing occurs.Consider the functionwhere δ＞ 0,so thatBy taking sufficiently large δ＞ 0,we then have,for any ρ ＞ 0,

If(2.3)occurs,the vanishing lemma[21,Lemma 1.21]then yields that

It then follows from(1.8)and(2.5)that

Following(2.5)and(2.6),we have

which is a contradiction to the fact(2.4).Therefore,Claim 1 holds.

Claim 2The functional e(ρ)satisfies the following strict sub-additivity condition

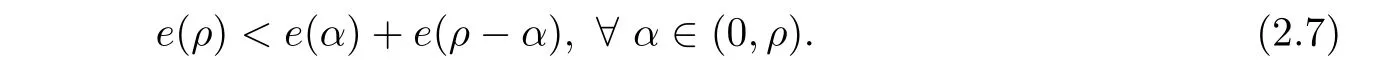
In order to prove(2.7),it suffices to prove that

Actually,if(2.8)holds,then(2.7)can be directly obtained by the following inequality

We now prove that(2.8)holds.Note from(2.1)and(2.2)that E(u)is bounded from below for any α ∈ (0,ρ).Suppose that{vn} ⊂ H1(R3)is a minimizing sequence of e(α)satisfyingandIt then follows from(2.1)and(2.2)that the sequence{vn}is bounded uniformly in H1(R3).Setting vθ,n(x):= θ12vn(x)such that ‖vθ,n‖22= θα,we thus obtain from(1.2)and(1.3)

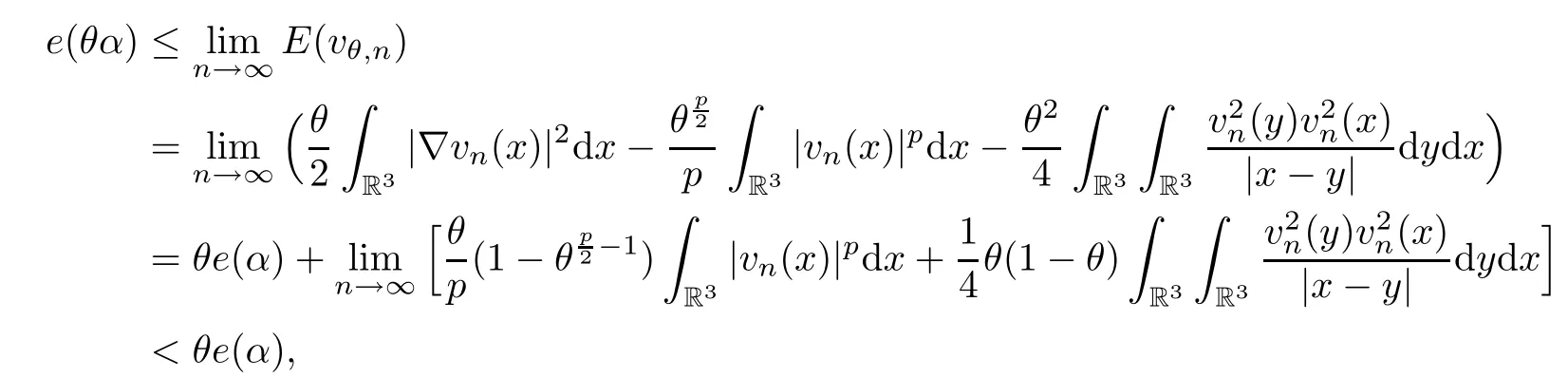
Claim 3The dichotomy of the minimizing sequence{un}cannot occur.

Similar to Theorem 4.1 in[2],we note that if eitherρ ∈ (0,ρ∗),then e(ρ)is continuous in ρ.Following the above results,we are now ready to exclude the dichotomy of the minimizing sequence{un}.Instead,if the dichotomy occurs,then there exist a sequence{yn}and some α ∈(0,ρ)such thatsatisfiesin R3for somewithThus,It is easy to check thatis also a bounded minimizing sequence of e(ρ),because E(u)is invariable to any translation of u.Asis bounded uniformly in H1(R3),the Brezis-Lieb lemma[4]and[23,lemma 2.2]yield that as n→∞,

and

By applying the continuity of e(ρ)and the last two equalities,we then derive that

which is a contradiction to Claim 2.Hence,the dichotomy of minimizing sequencecannot occur.

Claims 1 and 3 show that the minimizing sequenceis compact in L2(R3).We can select a subsequence,denoted still bysuch thatstrongly in L2(R3)for someBy applying(2.9)and the interpolation inequality,we conclude that

Therefore,from the above two equalities,one can obtain the weak lower semicontinuity ofand

(2)We next consider the rest two cases,where eitherρ ≥ ρ∗.Define

Letting τ→ ∞,inequalities(2.11)and(2.12)imply that e(ρ)= −∞ under the assumptions on p and ρ.Therefore,there is no minimizer for e(ρ).

Combining with(1)and(2),the proof of Theorem 1.1 is completed.

3 Blow-up Behavior as ρ ↗ ρ∗

This section is devoted to the proof of Theorem 1.2 on the mass concentration(that is,blow-up)behavior of minimizers for e(ρ)as ρ ↗ ρ∗.We begin with the following preliminary blow-up analysis.

Lemma 3.1Suppose that p=and let uρbe a nonnegative minimizer of e(ρ)for ρ ∈ (0,ρ∗).Define

Then,we have the followings:

1.∈ρ＞ 0 satisfies

2.There exist a sequence{y∈ρ} ⊂ R2and positive constants η and R0such that the function

satisfies

and

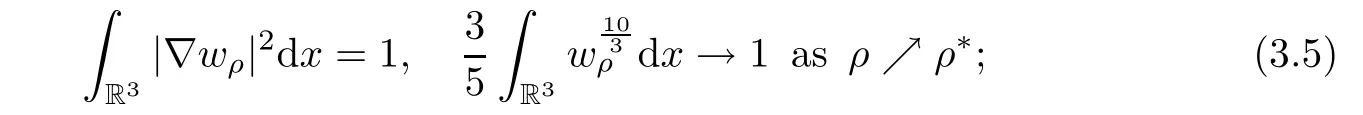
3.Moreover,consider any sequence ρkwith ρk↗ ρ∗,then there exists a subsequence(still denoted by ρk),such that wρkconverges to w0strongly in H1(R3)as k → ∞ and w0satisfies

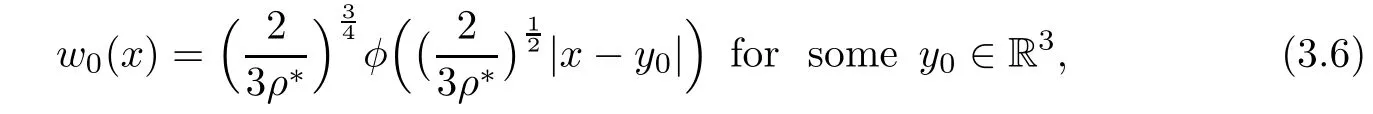
where φ(x)is the unique positive(up to translations)radially symmetric solution of(1.4).

Proof1.Note from(1.6)and(1.9)that

where(3.1)is used.As estimate(2.13)yields thatwe thus deduce from(3.7)that(3.2)holds.

2.By(1.9)and(3.2),we deduce that

Because(2.4)gives e(ρ)＜ 0,it then follows from(3.7)and(3.8)that

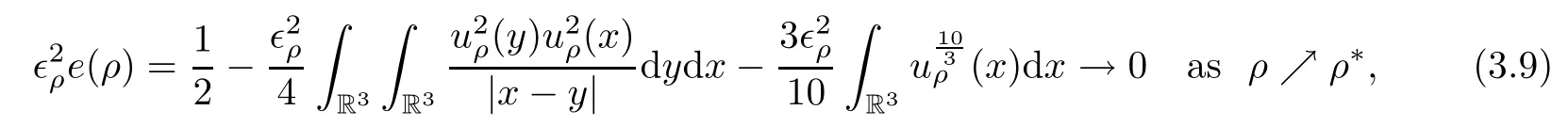
which implies that

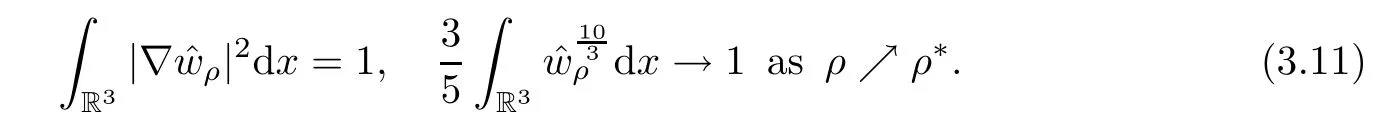
We next claim that there exist a sequence{y∈ρ} ⊂ R3and positive constants R0and η such that

On the contrary,suppose that the above inequality is false.Then,for any R＞0,there exists a subsequence{ˆwρk}with ρk↗ρ∗as k→∞such that

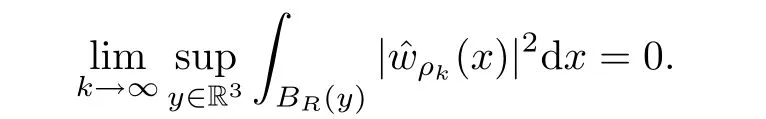
By the vanishing lemma[21,Lemma 1.21],we then derive thatˆwρk→0 in Lq(R3)for any 2＜ q＜ 2∗,which implies that

a contradiction to(3.11).Therefore,Claim(3.12)holds.Setting

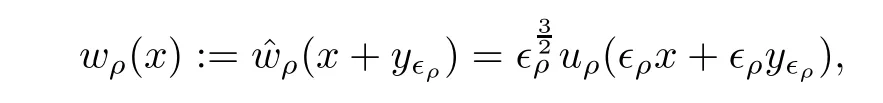
(3.11)together with(3.12)yields that(3.4)and(3.5)hold.

3.For any sequence ρkwith ρk↗ ρ∗,we denote ∈k:= ∈ρkand wk(x):=wρk(x).Because the sequence{wk}is bounded uniformly in H1(R3),by passing to a subsequence if necessary,wkweakly converges to w0≥0 in H1(R3)as k→∞,where w0(x)∈H1(R3).Because uk(x)=uρk(x)is a nonnegative minimizer of e(ρk),it satisfies the following Euler-Lagrange equation

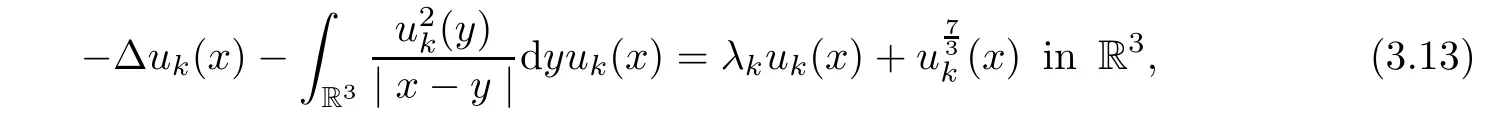
which implies that λk∈ R satisfies

Applying(3.8)-(3.10),we then deduce from the above equality that

Note from(3.13)that the function wk(x)satisfies

Inspired by[13],applying the Hölder inequality,we deduce that for any fixed R ＞ 0,

because of the uniform boundedness of sequence{wk}in H1(R3).On the basis of the above fact,by passing to the weak limit of(3.15),then w0satisfies

It follows from(3.4)that w0/=0,and further w0＞0 by strong maximum principle.Because equation(1.4)admits an unique(up to translations)positive solution φ(x),we conclude from(3.16)that

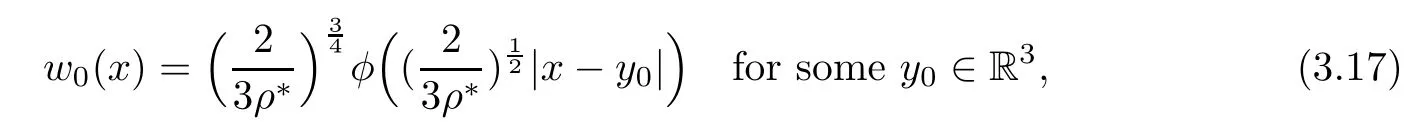
which then yields thatRR3|w0(x)|2dx= ρ∗.By the norm preservation,we derive that wkconverges to w0strongly in L2(R3).By applying the interpolation inequality,we further conclude that wkconverges to w0strongly in Lq(R3)with 2≤q＜2∗by the boundedness of wkin H1(R3).Because wkand w0satisfy(3.15)and(3.16),a simple analysis shows that wkconverges to w0strongly in H1(R3).The proof of Lemma 3.1 is therefore completed.

In order to estimate the refined blow-up rate of minimizers as ρ ↗ ρ∗,we next need to establish the following refined energy estimates of e(ρ)as ρ ↗ ρ∗.

Lemma 3.2Suppose that p=then for any sequence{ρk}satisfying ρk↗ ρ∗as k→∞,there holds

ProofFirstly,we establish the energy upper bound of e(ρ).Towards this aim,set

where φ(x)is the unique positive(up to translations)radially symmetric solution of(1.4).Similar to(2.12),we then calculate from(1.7)that

which thus gives the upper bound of(3.18).

To derive the energy lower bound of(3.18)as ρ ↗ ρ∗,consider uρ∈ H1(R3)to be a nonnegative minimizer of e(ρ)satisfyingSimilar to(2.2),one can deduce from(1.6)that

where ερis defined in(3.1)and wρis defined in(3.3).

It follows from(3.6)that,for any sequence{ρk}with ρk↗ ρ∗as k → ∞,passing to a subsequence if necessary,wρksatisfies

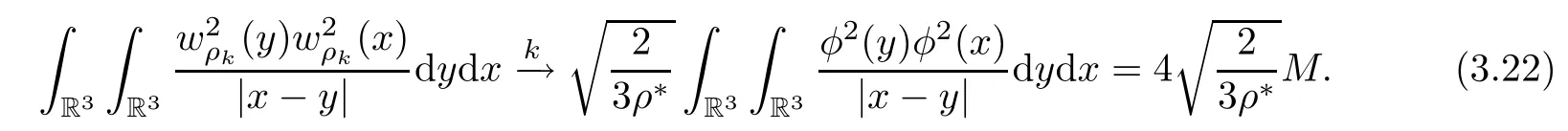
Thus,

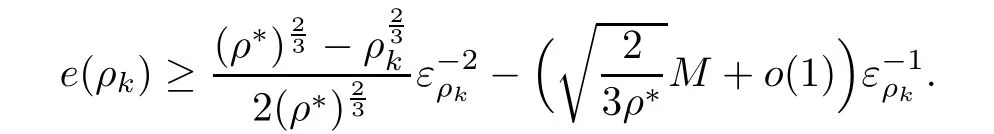
Taking the in fimum over ερk＞ 0,which is achieved at

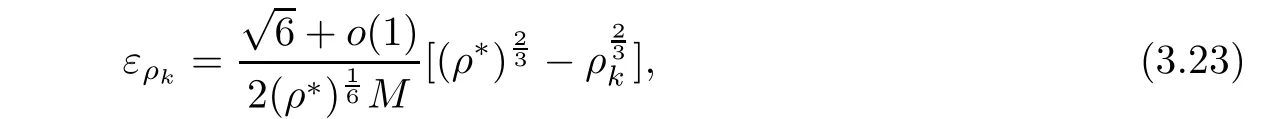
and yields that

One can also verify that(3.24)holds for any sequence{ρk}with ρk↗ ρ∗as k → ∞.In fact,if there exists a sequencesuch that(3.24)is false,by repeating the above argument,one can find a subsequence ofsuch that(3.24)holds.This leads to a contradiction.Hence,together with(3.20),this yields(3.18). □

Proof of Theorem 1.2In light of Lemma 3.1(3),for any sequence ρkwith ρk↗ ρ∗,then there exists a subsequence such that

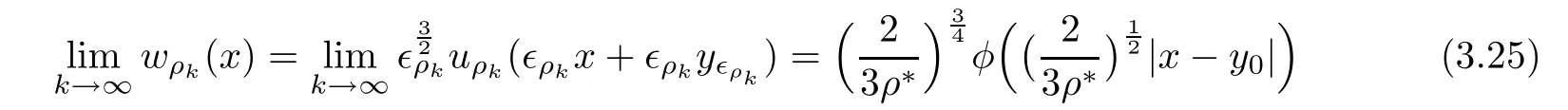
for some y0∈ R3,where φ(x)is the unique positive(up to translations)radially symmetric solution of(1.4).

By Lemma 3.2,for any sequence ρkwith ρk↗ ρ∗,we know that the refined energy estimate of e(ρ)satisfies

and we derive from(3.23)that

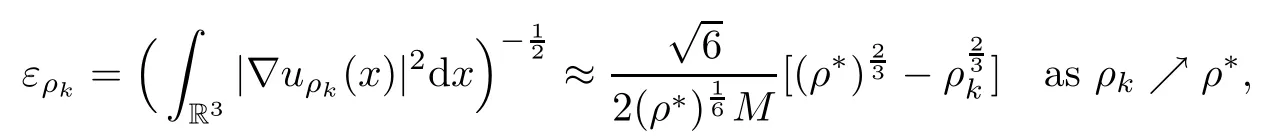
[1]Ambrosetti A,Ruiz D.Multiple bounded states for Schrödinger-Poisson problem.Comm Contemp Math,2008,10(3):391–404

[2]Bellazzini J,Siciliano G.Scaling properties of functionals and existence of constrained minimizers.J Funct Anal,2011,261(9):2486–2507

[3]Bokanowski O,Lopez J L,Soler J.On an exchange interaction model for quantum transport:the Schrödinger-Poisson-Slater system.Math Models Methods Appl Sci,2003,13(10):1397–1412

[4]Brézis H,Lieb E H.A relation between pointwise convergence of functions and convergence of functionals.Proc Amer Math Soc,1983,88(3):486–490

[5]Cao D M,Su Y M.Minimal blow-up solutions of mass-critical inhomogeneous Hartee equation.J Math Phys,2013,54(12):121511

[6]Catto I,Dolbeault J,Sánchez O,Soler J.Existence of steady states for the Maxwell-Schrödinger-Poisson system:exploring the applicability of the concentration-compactness principle.Math Models Methods Appl Sci,2013,23(10):1915–1938

[7]Guo Y J,Seiringer R.On the mass concentration for Bose-Einstein condensates with attactive interactions.Lett Math Phys,2014,104(2):141–156

[8]Guo Y J,Wang Z Q,Zeng X Y,Zhou H S.Properties of ground states of attractive Gross-Pitaevskii equations with multi-well potentials.arXiv:1502.01839,submitted,2015

[9]Guo Y J,Zeng X Y,Zhou H S.Energy estimates and symmetry breaking in attactive Bose-Einstein condensates with ring-shaped potentials.Ann Inst H Poincaré Anal Non Linéaire,2016,33(3):809–828

[10]Jeanjean L,Luo T J.Sharp nonexistence results of prescribed L2-norm solutions for some class of Schrödinger-Poisson and quasi-linear equations.Z Angew Math Phys,2013,64(4):937–954

[11]Kikuchi H.On the existence of a solution for elliptic system related to Maxwell-Schrödinger equations.Nonlinear Anal,2007,67(5):1445–1456

[12]Kwong M K.Uniqueness of positive solutions of Δu−u+up=0 in RN.Arch Rational Mech Anal,1989,105(3):243–266

[13]Lieb E H.Existence and uniqueness of the minimizing solution of choquard’s nonlinear equation.Stud Appl Math,1977,57(2):93–105

[14]Lions P L.The Choquard equation and related questions.Nonlinear Anal,1980,4(6):1063–1072

[15]Lions P L.The concentration-compactness principle in the caclulus of variations.The locally compact case.I.Ann Inst H Poincaré Anal Non Linéaire,1984,1(2):109–145

[16]Lions P L.The concentration-compactness principle in the caclulus of variations.The locally compact case.II.Ann Inst H Poincaré Anal Non Linéaire,1984,1(4):223–283

[17]Li Y,Ni W M.Radial symmetry of positive solutions of nonlinear elliptic equations in Rn.Comm Partial Differential Equations,1993,18(5-6):1043–1054

[18]Penrose R.On Gravity’s role in Quantum State Reduction.Gen Relativity Gravitation,1996,28(5):581–600

[19]Sánchez O,Soler J.Long-Time Dynamics of the Schrödinger-Poisson-Slater System.J Stat Phys,2004,114(1):179–204

[20]Weinstein M I.Nonlinear Schrödinger equations and sharp interpolations estimates.Comm Math Phys,1983,87(4):567–576

[21]Willem M.Minimax theorems.Springer Science&Business Media,1997

[22]Xiang C L.Quantitative properties on the steady states to a Schrödinger-Poisson-Slater system.Acta Math Sin English Ser,2015,31(12):1845–1856

[23]Zhao L G,Zhao F K.On the existence of solutions for the Schrödinger-Poisson equations.J Math Anal Appl,2008,346(1):155–169