基于移动粒子半隐式法的齿轮搅油损失分析与试验验证

李 晏， 皮 彪， 王叶枫， 刘林晶， 陈辛波,3

(1.同济大学 机械与能源工程学院， 上海 201804；2. 同济大学 汽车学院，上海 201804；3. 同济大学 新能源汽车工程中心， 上海 201804)

齿轮在机械行业中具有广泛的应用.在汽车传动系统中齿轮传动是主要组成部分.齿轮传动功耗可分为有载功耗和无载功耗.汽车在行驶过程中，主要处在高速低载的工况下，其功率损耗主要为以搅油损失为代表的无载损耗.因此研究齿轮搅油损失的内在特性对提高齿轮传动效率具有重要意义.

齿轮搅油损失与齿轮转速、浸油深度、润滑油运动黏度、工作温度等影响因素关系复杂，难以直接用理论分析确定，因此国内外对搅油损失的理论研究较少，大多数采用经验公式，用试验方法确定.Valeriy等[1]对齿轮传动无载荷功耗的经典文献进行了综述，整理了近半个世纪以来学者对搅油损失的计算公式，为后人进一步研究提供了参考.Attila等[2]研究表明，齿轮搅油功率损失主要包括驱动润滑油功率损失、飞溅功率损失以及搅油件功率损失，并分别给出了上述3种功率损失的计算公式.Chen等[3]通过试验发现，除了众所周知的因素外，齿轮和齿轮箱内壁的相对位置以及内壁形状都对搅油损失具有一定影响，分析过程中应该予以考虑.随着计算机技术的发展，数值模拟分析也被应用在搅油损失之中，Liu等[4-5]均运用有限体积法建立了三维有限体积CFD(computational fluid dynamic)模型来分析润滑油分布和搅油损失，并通过试验进行了验证.Gauthier等[6]中作者认为搅油损失与润滑油中的空气含量有关，并强调只通过密度和黏度来估算搅油损失是片面的，还应考虑其他因素.王飞[7]对齿轮搅油损失进行了理论研究与仿真分析，建立搅油损失的动态模型，用试验数据进行验证，并使之运用到了汽车轮边减速器上.霍晓强等[8]通过试验分别研究了油温、转速和浸油深度对搅油损失的影响，并指出油温变化对搅油功率损失影响不大，转速对功率损失的影响最大.梁文宏等[9]应用有限元流体力学软件Fluent对多组不同参数斜齿轮的三维搅油流场和搅油功率损失进行了数值仿真，并通过试验验证和比对证明了中低转速条件下可以使用仿真的方法预估搅油功率损失的数值.

以上文献得出的结果大多停留在经验公式层面，且相关公式的应用需要满足特定工况，具有较大局限性.而采用以网格为基础的有限元流体分析方法进行搅油损失分析不仅效率低下而且精度不高，效果不太理想.因此有必要采用其他方法对搅油损失进行研究.本文创新性地将移动粒子半隐式法运用到搅油损失研究当中，针对单齿搅油模型进行了齿轮搅油损失仿真，并通过试验验证了仿真结果的准确性，从而为搅油损失研究提供了一种有效的新途径.

1 斜齿轮搅油损失理论分析

齿轮搅油的主运动为齿轮在润滑油液中的旋转运动.对于斜齿轮搅油模型，油液的流动为斜齿轮端面和法面上的复合流动.为了建立齿轮搅油时润滑油液的流体力学动量方程和连续性方程，建立沿斜齿轮转角Θ、半径r和齿宽b方向的斜圆柱坐标系如图1所示.

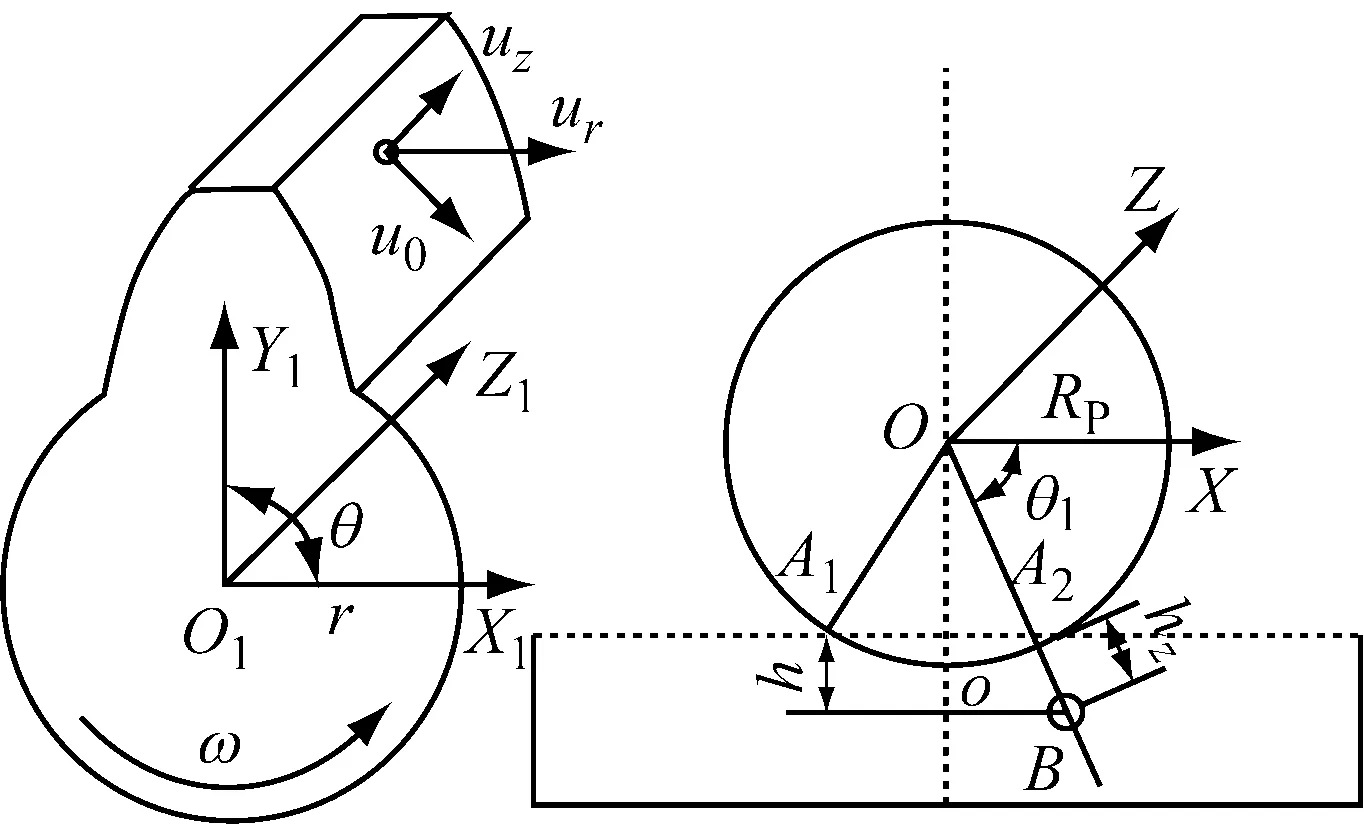
图1 斜齿轮搅油坐标系Fig.1 Coordinates of helical gear churning

图1中O为齿轮分度圆圆心；A1,A2为齿底圆与油液液面的交点；B为齿轮浸油最低点；h为浸油深度.

令油液沿坐标轴3个方向的流动速度分别为u，v，w，并以斜齿轮端面为基准，在考虑重力的情况下，利用纳维斯托克斯方程和边界层方程建立油液流动的流体力学动量方程和连续性方程为

(1)

式中：h为浸油深度，m；μ为润滑油动力黏度，kg·(m·s2)-1；ρ为润滑油密度，kg·m-3；RP为斜齿轮端面基圆半径，m；g为重力加速度，m·s-2.

流动边界条件为：壁面处y=0，u=RPω；无穷远处y=+∞，u=0，v=0.

齿轮搅油功耗的主要影响因素包括齿轮参数、润滑油参数及运行工况参数3部分，其中齿轮参数包含齿轮齿数z、模数mn、齿宽b和螺旋角β；润滑油参数包含润滑油运动黏度ν和润滑油密度ρ；运行工况参数包含齿轮转速ω、齿轮浸油深度h和当地重力加速度g.引入雷诺数Re和弗劳德数Fr，用齿轮节圆半径R替代z和mn的影响，则搅油损失Pchurn可表达成上述参数的函数

Pchurn=f(R,b,β,ν,ρ,ω,h,g,Re,Fr)

(2)

根据量纲分析π定理，选取R,ω,ρ为基本量纲.根据Seetharaman等[10]的分析，在诸多搅油损失影响因素中，较为显著的3个因素为：齿轮浸油深度、齿轮转动角速度和齿宽.故选取h,ω,b作为影响因素，并将其量纲归一化后得到齿轮轮搅油损失表达式如式(3)所示.

(3)

式中：Cm、A、B、C、D为待确定系数.为计算方便，公式中单位均采用国际单位制.

2 移动粒子半隐式法

2.1 基本原理

MPS(moving particle semi-implicit method)即移动粒子半隐式流体分析方法，是由东京大学Koshizuka等学者于20世纪90年代提出的求解不可压缩流体的无网格数值解法.使用该方法进行流体计算不需生成有限元网格，因而可以方便地模拟各类复杂流场.该方法以拉格朗日方法为基础，广泛适用于不可压缩流体的流动计算.该方法的基本原理是将流体计算区域视为由一群粒子构成，其中每个粒子都包含与之相对应的不同流动信息，并以拉格朗日方程为基础，求解各粒子间的相互作用关系方程和离散基本流动方程.由于粒子的物理场之间存在相对耦合关系，因此可根据各粒子上一时刻的流动信息对下一时刻进行预测和修正，随着时间步的推进，即可获得整个流场的动态流动信息[11].

2.2 控制方程及粒子作用模型

由于MPS以拉格朗日方法为基础，故给出拉格朗日形式下的流体运动质量和动量守恒方程

质量守恒方程

(4)

动量守恒方程

(5)

式中：u为流体速度矢量；ρ为流体密度；p为压力；μ为流体动力黏性系数；f为作用在流体单位质量上的外力矢量.方程左端均以拉格朗日时间微分形式表达，对流项包含在其中.

在MPS中，粒子通过核函数与周围粒子发生作用，这里给出Shakibaeinia等[12]建立的核函数

(6)

式中：rp是粒子之间的距离；re称为粒子作用半径.从式(6)中可以看出，当rp≥re时，粒子之间无相互作用，即粒子仅与位于其粒子作用半径re范围内的粒子发生相互作用，故核函数具有紧支集特性.

根据核函数，可得到粒子数密度模型、梯度矢量模型和拉普拉斯模型分别如下：

(7)

(8)

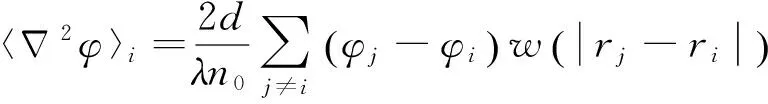
(9)

式(7)～(9)中：d为求解问题的空间维数；n0为粒子数密度常数；φ为粒子物理参数标量值；λ为修正因子.上述各模型的粒子作用半径re并不要求一致.

2.3 算法和边界条件

MPS方法采用半隐式时间推进算法.在每个时层内，首先显式计算动量方程中的黏性项及源项，得到粒子速度及位置的估算值，然后隐式求解连续方程获得粒子速度及位置的修正值，最终得到粒子在下一时层的速度及位置.通过对各个粒子在各时层运动规律的追踪，获得整个流场的流动信息.

与传统数值方法相比，MPS方法对边界条件的处理要容易许多.

使用MPS方法可以很容易判定自由表面.由于在自由表面的外部区域没有粒子存在，因此自由表面上粒子的粒子数密度较小.计算中凡满足

〈n*〉i<βn0

(10)

条件的粒子即可认为是自由表面粒子，其中β为一个小于1的常数.

对于固体壁面则可以很简便地以固定粒子表示，这些固定粒子速度总为0.为使流体粒子不进入固壁区域，固壁粒子中靠近流体的第一层粒子需与流体粒子一起参与压力计算，固壁粒子的层数则必须满足计算粒子团密度所需的层数[12].

3 斜齿轮搅油损失MPS分析

3.1 参数设置

如前所述，选取润滑油浸油深度、齿轮转速和齿轮齿宽3个变量作为斜齿轮单齿搅油损失的主要影响因素.在实际齿轮传动系统中，搅动润滑油产生飞溅润滑效果的齿轮主要是输出轴大齿轮，考虑实际汽车行驶工况，选定其转速分别为500、750和1 000 r·min-1，对应轮胎型号为205/55R16，车轮直径为631.9 mm，相应车速分别为60、90和120 km·h-1，涵盖了汽车日常使用中常见的中低速、中高速和高速不同工况，浸油深度和齿轮宽度对应地取3个常用值，如表1所示.所选齿轮相关参数如表2所示.

表1 影响因素参数Tab.1 Parameters of influencing factors

表2 斜齿轮参数Tab.2 Parameters of helical gear

润滑油选用85W/90的车用变速箱齿轮油，通过查询相关手册可知，润滑油密度ρ=900 kg·m-3;40 ℃时，运动黏度ν=1.82×10-4m2·s-1；100 ℃时，运动黏度ν=1.65×10-5m2·s-1.为便于与后文试验对照，取12 ℃的运动黏度ν=1.35×10-3m2·s-1.

3.2 分析结果

选用L9(34)正交表，运用MPS方法分析后得到各状态的搅油损失情况如表3所示.

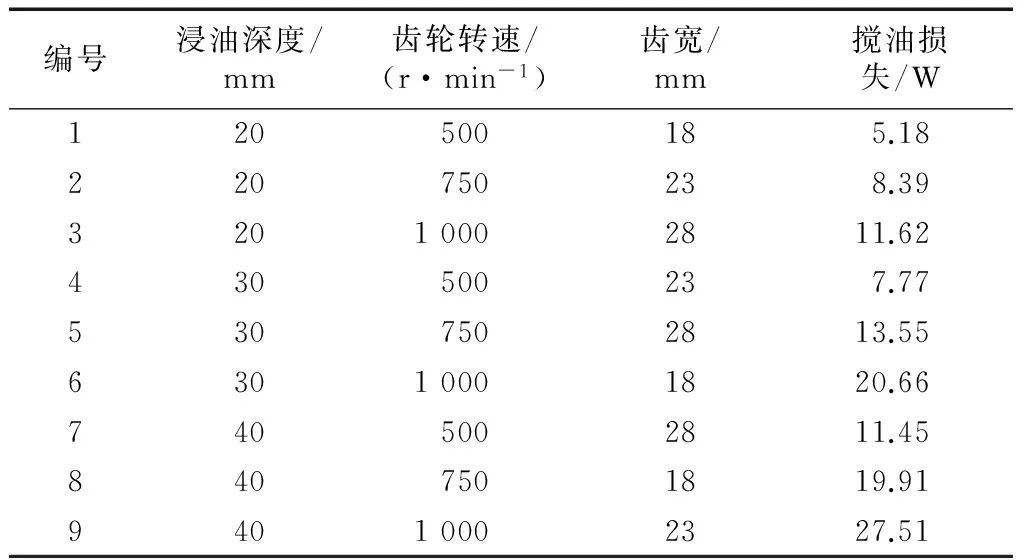
表3 各状态搅油损失Tab.3 Churning loss of each situation

由表3可得出浸油深度、齿轮转速、齿轮齿宽分别对搅油损失的影响如表4所示.各影响因素单独作用下的润滑油飞溅状态如图2所示.

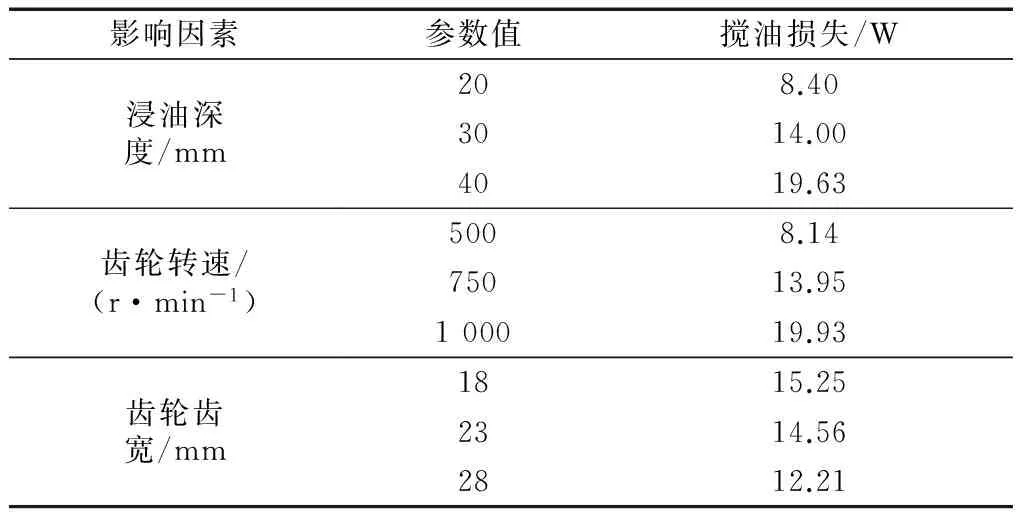
表4 各因素对搅油损失的影响Tab.4 Churning loss caused by eachinfluencing factors

从表4可得到：齿轮转速对搅油损失的影响最大；浸油深度对搅油损失的影响也较为显著；齿轮宽度对搅油损失的影响则不太明显.图2a为不同浸油深度下润滑油飞溅情况，从图中可以看出，随着浸油深度的增加，润滑油飞溅更加剧烈；图2b为不同齿轮转速下润滑油飞溅情况，润滑油飞溅趋势与图2a相似；图2c为不同齿轮宽度下润滑油飞溅情况，从图中可知不同齿宽下的润滑油飞溅情况对比不太明显.由此可说明表4与图2的结论相互吻合.

3.3 公式拟合

如前所述，将式(3)中的第1式两边取对数可得

(11)

a 不同浸油深度下润滑油飞溅情况

c 不同齿轮齿宽下润滑油飞溅情况图2 各影响因素单独作用下润滑油飞溅状态Fig.2 Lubrication change caused by eachinfluencing factors

将表3数据代入式(11)后，可得

Gx=y

(12)

x=[lnCmABCD]T

对式(12)进行最小二乘法求解可得单齿轮搅油损失拟合公式

(13)

式中：相关数据在求解前均已转换为国际单位制.

4 试验验证与误差分析

如图3所示斜齿轮单齿搅油试验台由伺服电机、联轴器、转速转矩传感器和单级齿轮箱组成.测试控制系统以D2P快速原型开发平台Motohawk为核心，上位机PC通过LABVIEW发送报文给Motohawk，Motohawk将报文处理后发送给伺服电机驱动器，驱动器控制电机运行，转速转矩传感器将检测到的转速转矩信号再经Motohawk发送给上位机PC处理，LABVIEW将接收到的转速转矩信号转化为搅油损失实时显示和记录.试验台架如图4所示.

图3 斜齿轮单齿搅油试验方案Fig.3 Experiment program of single helixgear churning loss

图4 斜齿轮单齿搅油试验台架Fig.4 Experiment rig of single helix gear churning loss

齿轮参数、润滑油黏度以及各影响因素均与前文MPS分析时保持一致.为消除随机误差对试验的影响，每组试验重复3次取平均值.

如前所述，选用如表3所示的正交表进行正交试验，得到各组的搅油损失与MPS分析结果对比如图5所示.

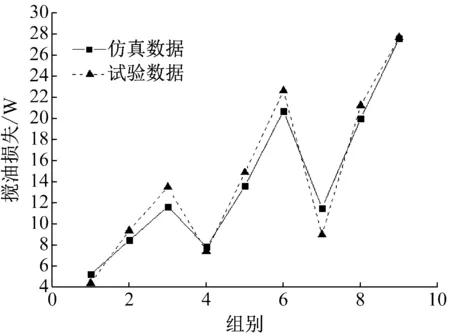
图5 试验与仿真结果对比Fig.5 Comparison between experiment and analysis

从图5可知试验与仿真结果吻合得较好，平均误差控制在10%以内，部分组别误差甚至达到1%以下.试验与仿真误差主要体现在以下方面：首先，试验中齿轮的转速波动、浸油深度的测量误差、齿宽的加工误差以及传感器的测量精度都会对搅油损失采集造成影响；其次，仿真分析中温度设定为恒定值，试验时由于试验环境的温度变化以及搅油过程中油液温度的变化也会对搅油损失造成影响.从试验与仿真的结果对比可以证明,MPS分析在齿轮搅油损失应用方面具有较好的可行性和准确性，为齿轮搅油损失进一步研究提供了一种有效的新方法.

5 结论

本文针对电动汽车传动系统无载功耗特性，通过对斜齿轮单齿搅油损失的理论分析、仿真和试验研究,得出以下结论：

(1)以浸油深度、齿轮转速和齿轮齿宽为变量建立了斜齿轮单齿搅油损失数学模型.

(2)运用移动粒子半隐式法(MPS)对齿轮搅油损失进行正交仿真分析，发现齿轮转速对搅油损失的影响最大；浸油深度对搅油损失的影响也较为显著；齿轮宽度对搅油损失的影响则不太明显.

(3)根据MPS分析结果，建立了斜齿轮单齿搅油损失计算公式.

(4)进行斜齿轮单齿搅油对照试验，发现试验数据和仿真数据吻合得较好.证明了MPS分析在搅油损失应用方面的可行性和准确性，为齿轮搅油损失进一步研究提供了一种有效的新方法.

参考文献:

[1] VALERIY Stavytskyy, PAVEL Nosko, PAVEL Fil,etal. Load-independent power losses of gear systems: a review [J]. TEKA Кom Mot I Energ Roln-OL PAN, 2010, 10B,205.

[2] ATTILA Csobán, MIHALY Kozma. Influence of the oil churning, the bearing and the tooth friction losses on the efficiency of planetary gears[J]. Nihon Geka Gakkai Zasshi, 2010, 86(3):290.

[3] CHEN S W, MATSUMOTO S. Influence of relative position of gears and casing wall shape of gear box on churning loss under splash lubrication condition-some new ideas[J]. Tribology Transactions, 2016, 59(6):993.

[4] LIU H, JURKSCHAT T, Lohner T,etal. Determination of oil distribution and churning power loss of gearboxes by finite volume CFD method[J]. Tribology International, 2017, 109:346.

[5] LIU H, JURKSCHAT T, LOHNER T,etal. Numerical modeling and validation of oil distribution and churning losses in gearboxes[C]∥ World Tribology Congress. Beijing:WTC,2017:2-4.

[6] GAUTHIER LePrince, CHRISTOPHE Changenet, FABRICE Ville,etal. Influence of aerated lubricants on gear churning losses-an engineering model[J]. Tribology Transactions, 2010, 54(6):929.

[7] 王飞. 电动汽车轮边减速器齿轮搅油损失研究与分析[D]. 淮南：安徽理工大学, 2015.

WANG Fei. Research and analysis of gear churning loss on the wheel-side reducer of electric vehicle[D]. Huainan: Anhui University of Science and Technology, 2015.

[8] 霍晓强, 吴传虎. 齿轮传动系统搅油损失的试验研究[J]. 机械传动, 2007, 31(1):63.

HUO Xiaoqiang, WU Chuanhu. Experimental investigation of churning loss of gear transmission system[J]. Journal of Mechanical Transmission, 2007, 31(1):63.

[9] 梁文宏, 刘凯, 崔亚辉. 基于有限元分析的斜齿轮搅油功率损失测算及实验验证[J]. 中国机械工程, 2014, 25(18):2510.

LIANG Wenhong, LIU Kai. Analysis and experimental investigation of helix gear churning loss base on finite element analysis [J]. China Mechanical Engineering, 2014, 25(18):2510.

[10] SEETHARAMAN S, KAHRAMAN A, MOORHEAD M D,etal. Oil churning power losses of a gear pair: experiments and model validation[J]. Journal of Tribology, 2009, 131(2):022202.

[11] 孙中国, 李帝辰, 陈啸,等. 移动粒子半隐式法在流体机械数值模拟中的应用[J]. 排灌机械工程学报, 2013, 31(11):921.

SUN Zhongguo, LI Dichen, CHEN Xiao,etal. Applicaiotn of moving particle semi-implicit method in mechanical numerical simulation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2013, 31(11):921.

[12] SHAKIBAEINIA A, JIN Y C. MPS mesh-free particle method for multiphase flows[J]. Computer Methods in Applied Mechanics & Engineering, 2012, 229-232(2):13.