城市轨道交通高峰时段站间起讫点矩阵预测模型
2018-05-04叶霞飞周利锋
成 艳, 叶霞飞, 王 治, 周利锋
(1. 同济大学 道路与交通工程教育部重点实验室, 上海 201804; 2. 重庆市轨道交通(集团)有限公司 信息部, 重庆 401120)
作为许多城市的交通骨干,城市轨道交通具有建设成本大,建成后修改难度高的特点,因此要求其规划设计具有前瞻性.作为城市轨道交通规划与设计阶段的关键指标,高峰小时单向最大断面客流量是确定车辆选型、列车编组等的重要依据.它由从高峰断面之前不同车站上车并在高峰小时内通过该断面的乘客组成,对高峰断面有贡献乘客的出发时刻均应在高峰小时及其之前.传统的高峰小时系数法未从形成机理出发,难以反映这一复杂的过程.为了克服这一缺点,需将时间范围从高峰小时扩展到高峰时段,并对高峰时段内出发的乘客选择的出发时刻与路径进行预测.为此,首先需确定高峰时段站间起讫点(OD)矩阵.
目前,学者们针对城市轨道交通站间OD矩阵估计已开展大量研究.这类研究基于AFC(Auto Fare Collection)票卡数据来反推站间OD矩阵[1-5].但由于规划与设计阶段尚不存在运营后的票卡数据,也无法进行路段或者车站客流量的观测,因此采用这一方法来预测远期的站间OD矩阵并不可行.
针对城市轨道交通高峰时段站间OD矩阵预测的研究则相对较少.Choi等[6]和Zhao等[7]均采用乘法模型对早高峰时段站间客流量进行预测.前者选取了表征车站周边建成环境、车站间交通阻抗、接驳设施等方面的32个变量作为自变量,并采用韩国首尔市轨道交通的数据对模型进行标定;后者则考虑了土地利用、接驳设施、车站属性、交通阻抗等方面的22个变量,采用中国南京市轨道交通的数据标定模型.虽然回归结果均较好,但这类模型不同于常规的交通分布模型,理论基础较为薄弱,无法保证预测的站间客流量满足出行发生和出行吸引约束条件,且对数据的获取要求较高,接驳设施方面的部分自变量在规划与设计阶段也难以确定.
常规的交通分布预测模型主要以全天为时间范围,关注的是全方式交通分布.其中一类重要的方法为重力模型[8-9],它因其简约的数学形式和易于处理的优点被广泛使用,但也存在交通阻抗较小时预测值偏高等缺陷.这一模型是否适用于城市轨道交通高峰时段站间OD矩阵预测尚待验证.
在城市轨道交通规划与设计中,远期全天站间OD矩阵采用“四阶段”方法预测,即将全方式OD矩阵进行交通分配后确定,它不受时间推移的影响,预测精度相对较高.因此以预测的全天站间OD矩阵已知为前提,以中国重庆市为研究范围,首先实证分析了传统的重力模型在城市轨道交通高峰时段站间OD矩阵预测中的优、缺点.在此基础上,进一步提出了改进的高峰时段站间客流OD矩阵预测模型.基于重力模型推导出站间客流高峰时段系数的表达式,将该系数的预测结果与全天站间客流量相乘即可形成高峰时段站间OD矩阵.利用同一数据源对不同配置的模型进行标定,并将其预测结果与传统的重力模型比较.
1 研究对象及范围
1.1 研究对象
重庆市位于中国内陆西南部、长江上游地区,面积8.24万km2,常住人口2991.4万人,常住人口城镇化率59.6%,其中主城建成区面积650 km2,常住人口818.98万人.截至2015年底,重庆市范围内共有4条运营的轨道交通线路,其中1、6号线为地铁制式,2、3号线为单轨制式,运营里程为202 km.线网覆盖重庆主城区全域,共设站点120个.通过剔除进、出站客流量为0的车站并将换乘站点合并,共有车站110座.由于光电园站周边土地利用存在重大变化,九曲河站周边土地利用尚处于开发阶段,因此这两个站不在研究对象之列.本文的研究对象为重庆市轨道交通的108座车站.
1.2 数据来源
为了比较不同的高峰时段站间OD矩阵预测模型的表现,采用同一数据源,主要包括:①前提条件:研究对象之间的全天站间OD矩阵.②因变量:研究对象之间的高峰时段站间OD矩阵.③自变量:研究对象的分时段进/出站客流量,两站间的时间最短路径的旅行时间和换乘次数.
全天及高峰时段站间OD矩阵和分时段进、出站客流量根据重庆市轨道交通(集团)有限公司提供的2015年8月26日票卡数据统计得到.不论是站间客流量还是进、出站客流量,均根据乘客进站时刻划分至相应时段.这意味着只要乘客进站时刻位于高峰时段内,不论其何时出站,这次出行都会被归入高峰时段.经统计,站间客流量不为0的车站对数为8 669对.
随着网络不断扩张,两站之间供乘客选择的路径可能不只一条.乘客在选择路径时会从中挑选出对于感知阻抗最小的路径,因此同一OD对之间被选择的多条路径虽然对于不同类型的乘客而言阻抗大小不同,但彼此之间的差值不会太大,且路径选择对乘客的起始站和目的站选择并不会产生本质影响.因此为了保证数据一致性,选用两站间的时间最短路径作为代表,其信息根据重庆市轨道交通的网络基本情况(包含线路及车站信息、站间运行时间、停站时间、换乘时间等)采用Dijkstra算法计算得到.
1.3 高峰时段的界定
轨道交通具有快速、准时、大运量的特点,因此承担了大量中长途出行的上下班、上下学乘客的运输工作.该类乘客具有刚性出行需求,目的地规定到达时刻固定且较为相近,致使城市轨道交通线路的高峰时段往往出现在早高峰.重庆市轨道交通也符合这一规律,4条线路的高峰小时均出现在上午8:00—9:00,如图1所示.
乘客的出行是一个过程,其开始时刻和终止时刻可能位于两个不同的时段(高峰时段或非高峰时段).因此,不同的划分标准可能导致同一出行属于不同的时间段内.本研究根据乘客的进站时间来判断本次出行归入哪一个时间段.由于高峰小时单向断面客流量是由高峰小时及其之前从各个车站出发的乘客出行叠加产生的,所以高峰时段的起始时间应早于单向最大断面高峰小时的起始时间,将其定为上午6:00—9:00.
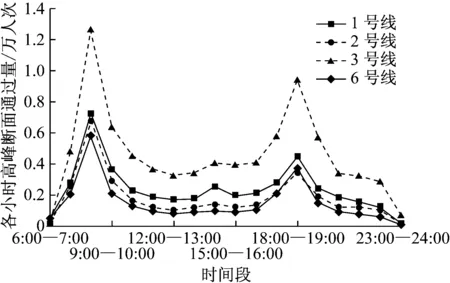
图1 重庆市轨道交通工作日各小时单向最大断面通过量
Fig.1Maximumsingle-directionsectionpassengerflowoflinesinChongqingrailtransitononeweekday
2 高峰时段站间OD矩阵预测模型
2.1 交通阻抗
高峰时段站间OD矩阵预测中,交通阻抗是一个不可忽视的重要因素,其函数形式和组成项不同,会直接影响最终的模型标定结果.目前常用的交通阻抗函数形式主要有幂函数型、指数函数型、组合函数型3种,应用在城市轨道交通中.
形式1:幂函数型
(1)
形式2:指数函数型
f(cij)=f(dij)=exp(-ηdij)
(2)
形式3:组合函数型
(3)
式(1)~(3)中:cij为车站i、j之间的广义出行费用;dij为车站i、j之间的旅行时间;γ、η为待定系数.
城市轨道交通不同于道路交通和常规公交,乘客只能通过换乘站在不同线路之间转换.因此整个系统的特征决定了在衡量两个车站之间的交通阻抗时,除了两站之间的旅行时间,换乘次数也是十分重要的影响因素.由于幂函数中,当指数小于0时,底数不能为0,而两站之间的换乘次数为非负整数,因此不宜以幂函数形式引入交通阻抗.本文采用指数函数形式在交通阻抗函数中引入换乘次数.
形式4:
nij)
(4)
形式5:
f(cij)=f(dij,nij)=exp(-ηdij-τnij)
(5)
形式6:
(6)
式中:nij为车站i、j之间的换乘次数;τ为待定系数.
交通阻抗函数中的站间旅行时间和换乘次数均为OD对之间时间最短路径的相应值.为了深入研究交通阻抗函数对于高峰时段站间OD矩阵预测的影响,后续预测模型将采用这6种形式的交通阻抗函数分别进行标定.
2.2 重力模型
2.2.1模型构建
重力模型根据牛顿的万有引力定律类推而成.在城市轨道交通的背景下,依照重力模型思想可认为两个车站之间的站间客流量与起始站的进站量、目的站的出站量成正比,而与车站之间的交通阻抗成反比.最早出现的无约束重力模型,不满足交通守恒约束条件.基于此模型[9],高峰时段站间客流量可表示为
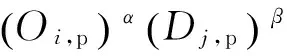
(7)
式中:tij,p为高峰时段从车站i进站并在车站j出站的客流量;Oi,,p为高峰时段从车站i进站的客流量;Dj,p为高峰时段从其他车站进站并在车站j出站的客流量;f(cij,p)为高峰时段车站i、j之间的交通阻抗函数;k、α、β为待定系数.
在此基础上加入出行发生约束,形成了单约束重力模型[10],则高峰时段站间客流量可表达为
(8)
式中:ρ为待定系数.
2.2.2标定结果
无约束重力模型中,通过对公式(7)两边取对数的方式将方程线性化后,采用最小二乘法标定系数.
lntij,p=lnk+αlnOi,p+βlnDj,p+lnf(cij,p)
(9)
式中:lnf(cij,p)随交通阻抗函数变化,但始终为lndij,p、dij,p和nij,p的线性组合.
单约束重力模型的参数标定过程参见文献[11].最终标定的线性方程如公式(10)~(13)所示.
(10)
(11)
(12)
(13)
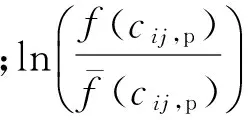
采用中国重庆市数据,对以上变量进行K-S检验,其渐近显著性均小于0.050,不服从正态分布.采用Spearman相关分析得到的结果表明不论是无约束还是单约束重力模型,自变量均与因变量呈显著相关,相关系数较大,且相关方向与模型推导结果一致(如表1、表2所示).相比而言,单约束重力模型的自变量与因变量之间的相关系数普遍高于无约束重力模型.

表1 无约束重力模型变量相关系数Tab.1 Bivariate correlation analysis of unconstrained gravity models
注:**在置信度(双测)为 0.01 时,相关性是显著的.

表2 单约束重力模型变量相关系数Tab.2 Bivariate correlation analysis of production-constrained gravity models
注:**在置信度(双测)为 0.01 时,相关性是显著的.
重力模型框架主要包含无约束和单约束重力模型.第一类包含了12个模型,差异为模型中k值是否为1和交通阻抗函数;第二类默认不含常数项,因此只有6个模型,差异仅为交通阻抗函数.基于案例数据,对这18个模型进行参数标定.为了保证预测的站间客流量满足进站端和出站端约束条件,预测结果均采用福莱特法进行迭代计算.
评判模型预测能力的标准采用高峰时段站间客流量的标准误差σ,如公式(14)所示.
(14)
式中:εl为第l对车站的站间客流量实际值与预测值误差;n为高峰时段站间客流量不为0的车站对数.
参数标定结果如表3、表4所示.部分模型存在变量未通过显著性检验的情况,主要是因为交通阻抗函数中存在两项与站间旅行时间相关的变量,当站间旅行时间对站间客流量的影响效果集中于其中一项时,使得另一项无法通过显著性检验.
由图2可知,对于同一类重力模型,阻抗函数形式相同的情况下,交通阻抗函数含换乘次数的重力模型预测结果均优于交通阻抗函数不含换乘次数的重力模型,证明城市轨道交通中,交通阻抗函数有必要考虑换乘次数的影响.重力模型框架中,采用形式5的交通阻抗函数且k=1的无约束重力模型最优,其标准误差为29.33人次.

表3 无约束重力模型系数Tab.3 Parameters of unconstrained gravity models
注:下划线表示该变量未通过显著性检验.

表4 单约束重力模型系数Tab.4 Parameters of production-constrainedgravity models
注:下划线表示该变量未通过显著性检验.
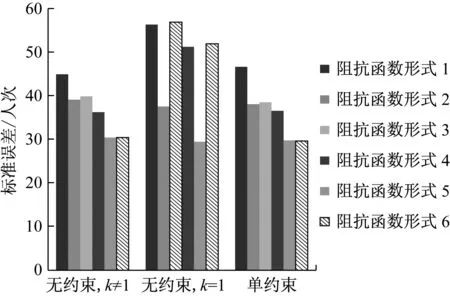
注:斜线填充的模型存在变量未通过显著性检验图2 重力模型标准误差Fig.2 Standard deviation of gravity models
2.2.2模型分析
虽然传统的重力模型被广泛使用,但它也存在以下缺点:①欠缺对出行者行为的分析;②阻抗小时有预测过高的可能性;③小区内部交通量难以预测;④出行距离在全区域并非定值;⑤交通小区之间的阻抗因交通方式差异较大.
当这一方法应用于城市轨道交通高峰时段站间OD矩阵预测时,预测对象从交通小区变成轨道交通车站,不再具有空间范围概念,出行者从原来区域之间的移动变为点之间的移动.此时,①车站本身不存在内部交通量;②只存在轨道交通这一种交通方式,不存在由于交通方式不同导致的阻抗差异;③轨道交通网络的自身特征使得站间距离为定值,因此较好地规避了后3个缺点.但另一方面,由于交通方式从全方式缩减为城市轨道交通这一单一方式,使得缺点②被进一步放大.当两个车站之间的交通阻抗较小时,因为交通费用等原因,其间的客流转换到常规公交、慢行交通方式上的可能性更大,使得城市轨道交通系统中,这两站之间的客流量下降.而采用重力模型进行预测时,站间客流量严格遵守随阻抗减小而增大的趋势,这就导致交通阻抗较小时,预测值偏高的程度加剧.
2.3 站间客流高峰时段系数模型
2.3.1模型构建
为了改善传统的重力模型在预测高峰时段站间OD矩阵时存在的交通阻抗较小带来的预测值偏高的问题,提出了站间客流高峰时段系数模型.该模型通过预测站间客流高峰时段系数这一相对值,并将其与已知的全天站间OD矩阵相乘得到预测的高峰时段站间OD矩阵.站间客流高峰时段系数是指高峰时段站间客流与全天站间客流的比值.不同时段的乘客出行目的差异较大,对于早高峰时段的乘客而言,其出行目的主要为上班和上学,因此以居住用地为主的车站和以岗位用地为主的车站之间有较大的站间客流量;而对于全天而言,乘客中除了包含早高峰时段的乘客,还包含了平峰时段车站附近居民休闲、娱乐等弹性需求出行的乘客和晚高峰时段在车站附近工作回家的乘客等.城市轨道交通车站周边的土地利用多样化使得高峰时段站间OD矩阵不能通过单纯地直接将全天站间OD矩阵乘以同一个站间客流高峰时段系数转换得到,还需考虑起始站、目的站自身的属性.
假定站间客流量服从无约束重力模型,则站间客流高峰时段系数可表示如下:
(15)
式中:Pij为车站i、j的站间客流高峰时段系数;tij,p为高峰时段从车站i进站并在车站j出站的客流量;tij,d为全天车站i、j的站间客流量;Oi,p为高峰时段从车站i进站的客流量;Oi,d为全天车站i的进站客流量;Dj,p为高峰时段从其他车站进站并在车站j出站的客流量;Dj,d为全天车站j的出站客流量;f(cij,p)、f(cij,d)分别为高峰时段、全天车站i、j之间的交通阻抗函数.
(16)

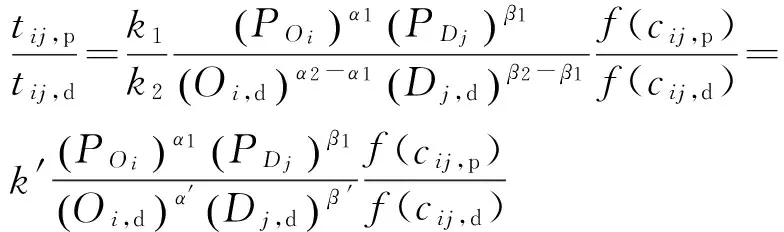
(17)
式中:POi为高峰时段车站i的进站客流比例;PDj为高峰时段车站j的出站客流比例;k′、α1、β1、α′、β′为待定系数,其中k′=k1/k2,α′=α2-α1,β′=β2-β1.
由式(17)可以看出高峰时段起始站进站客流比例、高峰时段目的站出站客流比例、起始站全天进站量、目的站全天出站量和交通阻抗是影响高峰时段系数的因素.其中后3项自变量可以由已知条件计算得到,而高峰时段起始站进站客流比例和高峰时段目的站出站客流比例需结合车站周边的社会经济、土地利用情况预测得到[12].
基于公式(17),可以得到最终的站间客流高峰时段系数模型为
(18)
若模型增加以下假定,公式(18)可进一步简化.
(1)无约束重力模型中,系数k可以看作是除了进、出站量和交通阻抗影响外,对站间客流大小起到影响的其他因素的综合修正系数.假定不同时段的站间客流仅受到起始站进站量、目的站出站量和两站间交通阻抗影响,即k1=k2,k′=1,则公式(18)可简化为
(19)
(2)交通阻抗函数通常为站间旅行时间、换乘次数的函数.由于城市轨道交通系统中,线路和车站一旦建成,站间旅行时间和换乘次数这两项自变量在不同时段几乎没有变化,若假定不同时段的交通阻抗一致,即f(cij,p)=f(cij,d),则公式(18)可简化为
(20)
上述假定是否成立,需结合实际进行分析.
2.3.2标定结果
因为全天站间OD矩阵为已知条件,所以模型的预测项为站间客流高峰时段系数.对公式(17)两边取自然对数后,得到公式(21).
lnPij=lnk′+α1lnPOi+β1lnPDj-α′lnOi,d-
β′lnDj,d+lnf(cij,p)-lnf(cij,d)
(21)
方程线性化后,采用最小二乘法即可标定系数.
表5表明相关方向与站间客流高峰时段系数模型相符,所有自变量均与因变量显著相关.相关系数方面,lnPOi、lnPDj较大,lnOi,d、lnDj,d次之,dij,p、lndij,p、nij,p较小.相较于传统的重力模型,dij,p、lndij,p、nij,p的相关系数明显降低,证明这3个自变量对于站间客流高峰时段系数模型的影响减弱.
站间客流高峰时段系数模型根据两项假定是否成立和交通阻抗函数形式,可衍生出14个模型.基于案例数据,对这14个模型进行参数标定.同样地,为了保证预测的站间客流量满足进站端和出站端约束条件,预测结果均采用福莱特法进行迭代计算.
剔除了未通过变量显著性检验的模型后,站间客流高峰时段系数模型中表现最优的是采用形式3的交通阻抗函数且k′≠1的模型,标准误差为12.90人次.高峰时段车厢拥挤度较大,虽然是同样的站间旅行时间,但乘客感知的站间旅行时间可能会被放大,因此高峰时段和全天的交通阻抗有所差异,进而影响到高峰时段系数.
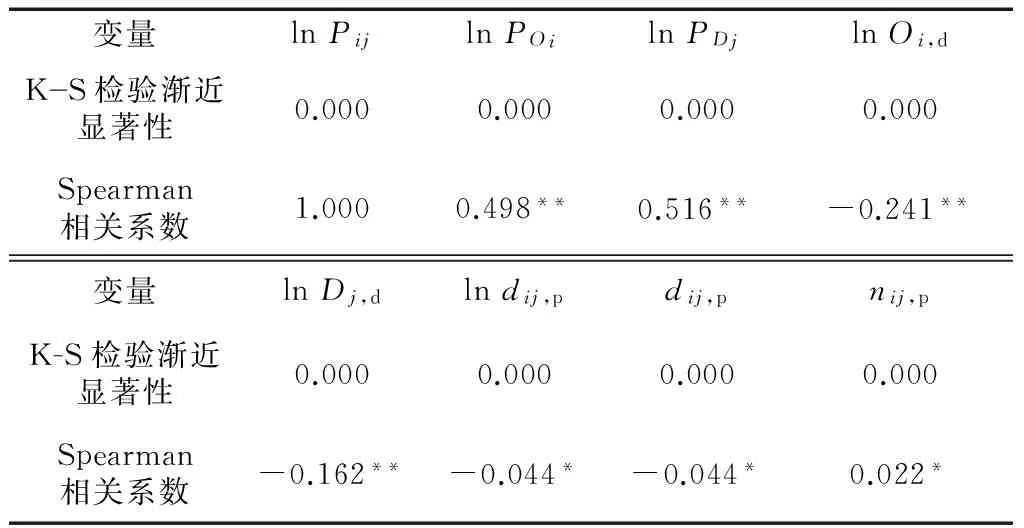
表5 站间客流高峰时段系数模型变量相关系数Tab.5 Bivariate correlation analysis of peak periodcoefficient (PPC) models
注:**在置信度(双测)为 0.01 时,相关性是显著的;*在置信度(双测)为 0.05 时,相关性是显著的;dij,p=dij,d,nij,p=nij,d,因此不再单独分析全天站间旅行时间和换乘次数与因变量的相关性.
标定结果表明,除了组合函数形式的交通阻抗函数,采用其余形式的交通阻抗函数的模型中,k′=1与k′≠1的模型的标准误差绝对值之差均小于1人次.因此在对预测精度要求不是很高时,可以默认假定(1)成立.而对于假定(2)是否成立主要有两方面依据.首先,如表6所示,未通过显著性检验的变量主要为nij,p和dij,p.换乘次数不论在高峰时段还是全天都不会变化,因此它对于因变量的影响微乎其微.站间旅行时间方面,当dij,p或lndij,p单独出现在模型中时,回归系数绝对值较小或未通过显著性检验,而当两者同时出现在模型中时,符号相反,使得其影响相互抵消.因此站间旅行时间对于因变量的影响也较小.其次,不同形式的交通阻抗函数标定的结果之间不存在较大差异,且与不含交通阻抗函数的模型结果也比较相近,如图3所示.不含交通阻抗函数的模型标准误差为13.30人次,略逊于该框架下的最优模型,但仍优于其他大部分模型.因此,当预测精度要求不是很高时,可认为假定(2)成立.
3 模型比较
两种模型框架中最优模型见式(22)、(23).
重力模型:
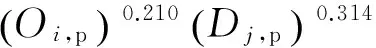
0.730nij,p)
(22)
站间客流高峰时段系数模型:
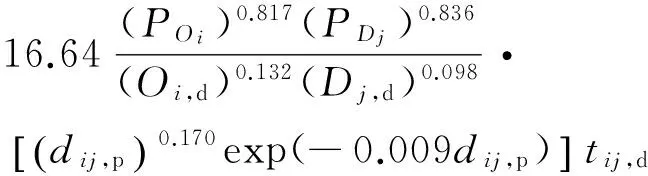
(23)
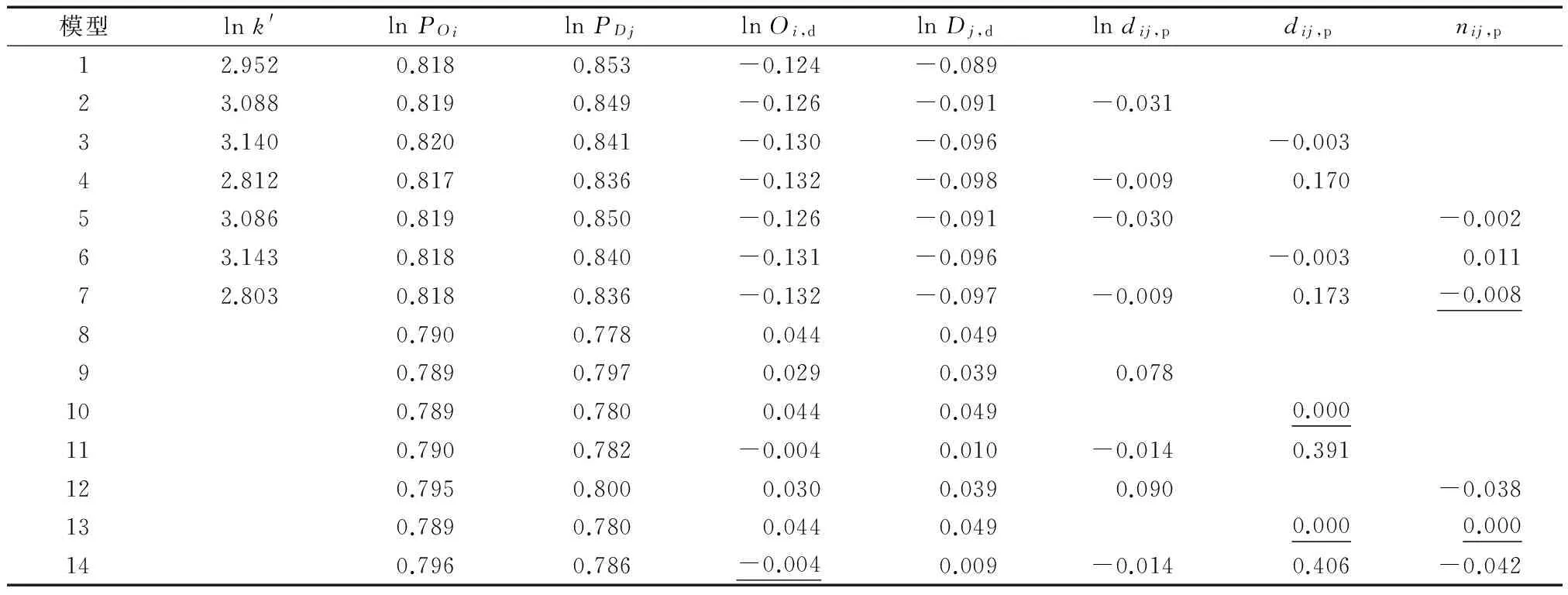
表6 站间客流高峰时段系数模型系数Tab.6 Parameters of PPC models
注:下划线表示该变量未通过显著性检验.
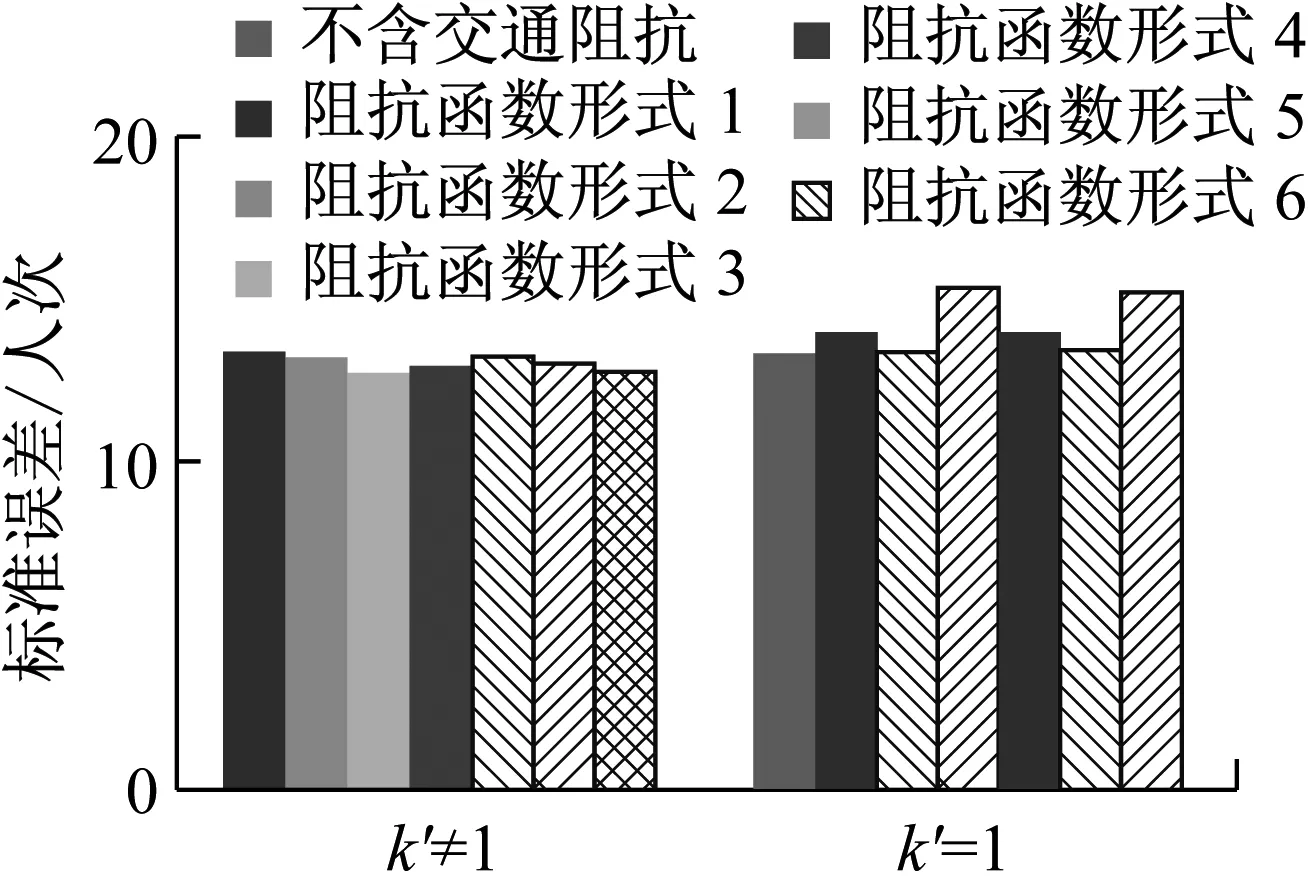
注:斜线填充的模型存在变量未通过显著性检验图3 站间客流高峰时段系数模型标准误差Fig.3 Standard deviation of PPC models
以实际站间客流量为基准,图4、图5给出了两个模型结合福莱特法迭代得到的预测结果的误差.图4中45°对角线附近的车站之间交通阻抗较小,大部分两站之间客流量误差较大的情况集中在这一条对角线附近,而这一点在图5中得到了明显改善.将站间旅行时间不大于5 min且无换乘的车站对定义为小阻抗车站对.由表7可知,重力模型预测得到的小阻抗站间客流量平均预测误差高达29.95人次,而站间客流高峰时段系数模型中,该值仅为-0.54人次.可见,站间客流高峰时段系数模型中,交通阻抗过小的影响通过比值的形式得到削弱,因此能够有效改善预测值偏高的问题.
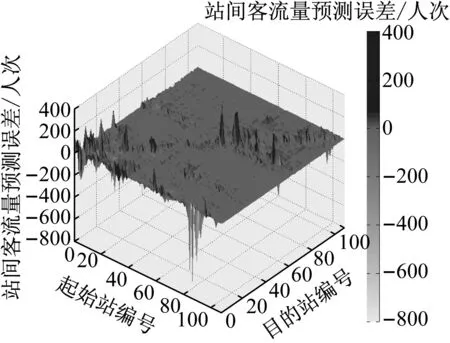
图4 重力模型预测误差Fig.4 Forecast deviation of gravity model

图5 站间客流高峰时段系数模型预测误差Fig.5 The forecast deviation of the PPC model表7 模型误差统计Tab.7 Statistics of model deviations
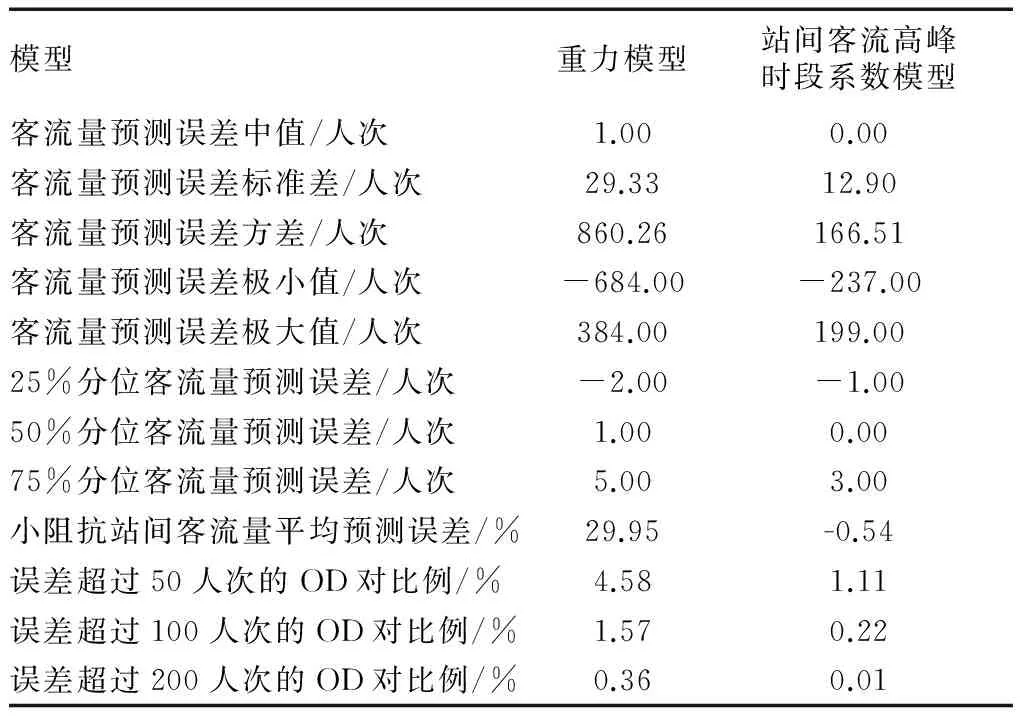
模型重力模型站间客流高峰时段系数模型客流量预测误差中值/人次1.000.00客流量预测误差标准差/人次29.3312.90客流量预测误差方差/人次860.26166.51客流量预测误差极小值/人次-684.00-237.00客流量预测误差极大值/人次384.00199.0025%分位客流量预测误差/人次-2.00-1.0050%分位客流量预测误差/人次1.000.0075%分位客流量预测误差/人次5.003.00小阻抗站间客流量平均预测误差/%29.95-0.54误差超过50人次的OD对比例/%4.581.11误差超过100人次的OD对比例/%1.570.22误差超过200人次的OD对比例/%0.360.01
此外,结合上述图表可知,不论是整体还是个案,站间客流高峰时段系数模型均明显优于重力模型,其标准误差相对于重力模型减少了16.43人次,降幅达56.02%.
4 结论
以中国重庆市为例,结合实证分析提出了基于重力模型的城市轨道交通高峰时段站间OD矩阵预测模型.在全天站间OD矩阵已知的前提下,通过预测站间客流高峰时段系数,将其与全天站间客流量相乘得到相应的高峰时段站间客流量.研究表明:
(1) 传统的重力模型应用于城市轨道交通高峰时段站间OD矩阵预测时,虽然能较好地规避自身存在的诸多缺点,但由于交通方式由全方式缩减为单一方式,使得交通阻抗较小时预测值偏高这一问题反而加剧.
(2) 以相对值为因变量的站间客流高峰时段系数模型能有效改善交通阻抗较小时造成的预测值偏高问题,模型的预测能力明显优于传统的重力模型,标准误差降低56.02%.
(3) 站间客流高峰时段系数模型中,换乘次数不是其主要影响因素,且不含交通阻抗函数的模型与其他不同形式的交通阻抗函数之间的预测表现较为相近,说明对于城市轨道交通而言,不同时段的交通阻抗函数可能存在差异,但对于高峰时段系数的影响并不明显.
当模型应用于城市轨道交通的规划与设计阶段时,站间客流高峰时段系数模型中的高峰时段起始站进站客流比例、高峰时段目的站出站客流比例这两项自变量可基于车站周边的社会经济或土地利用情况预测获得.
参考文献:
[1] WONG S C, TONG C O. Estimation of time-dependent origin-destination matrices for transit networks[J]. Transportation Research Part B: Methodological, 1998,32(1):35.
[2] NUZZOLO A, CRISALLI U. Estimation of transit origin/destination matrices from traffic counts using a schedule-based approach[C/OL]∥Proceedings of The Aet European Transport Conference.[2017-01-10].https:∥aetransport.org/en-gb/past-etc-papers/conference-papers-pre-2009/conference-papers-2001?search=Estimation&abstractId=1327&state=b.
[3] GORDILLO F. The value of automated fare collection data for transit planning: an example of rail transit od matrix estimation[D]. Cambridge:Massachusetts Institute of Technology, 2006.
[4] ZHAO J, RAHBEE A, WILSON N H. Estimating a rail passenger trip origin-destination matrix using automatic data collection systems[J]. Computer-Aided Civil and Infrastructure Engineering, 2007, 22(5):376.
[5] 姚向明, 赵鹏, 禹丹丹. 基于平均策略的城市轨道交通动态O-D矩阵估计[J]. 吉林大学学报(工学版), 2016,46(1):92.
YAO Xiangming, ZHAO Peng, YU Dandan. Dynamic origin-destination matrix estimation for urban rail transit based on averaging strategy[J].Journal of Jilin University (Engineering and Technology), 2016,46(1):92.
[6] CHOI J, LEE Y J, KIM T,etal. An analysis of metro ridership at the station-to-station level in Seoul[J]. Transportation, 2012,39(3):705.
[7] ZHAO J, DENG W, SONG Y,etal. Analysis of metro ridership at station level and station-to-station level in Nanjing: an approach based on direct demand models[J]. Transportation, 2014,41(1):133.
[8] WILSON A G. A family of spatial interaction models, and associated developments[J]. Environment and Planning A, 1971,3(1):1.
[9] 邵春福.交通规划原理[M].北京:中国铁道出版社, 2004.
SHAO Chunfu. Traffic planning[M]. Beijing: China Railway Publishing House, 2004.
[10] VOORHEES A M. A general theory of traffic movement[J].Transportation,2013,40(6):1105.
[11] NAKANISHI M, COOPER L G. Parameter estimation for a multiplicative competitive interaction model: least squares approach[J]. Journal of Marketing Research, 1974,11(3):303.
[12] CHENG Y, YE X, WANG Z. A forecasting model of the proportion of peak-period boardings for urban mass transit system: a case study of osaka prefecture[C/CD]∥Transportation Research Board 95th Annual Meeting.Washington D C:Transportation Research Board, 2016.
