基于广义改进型RBF网络的射频功放非线性建模

江明玉，刘太君，叶焱，许高明

（宁波大学信息科学与工程学院，浙江 宁波 315211）

1 引言

为了高效利用频谱资源，现代通信多采用大带宽和多载波调制信号。这类信号经过射频功率放大器（RFPA, Radio Frequency Power Amplifier）时，会产生很严重的记忆非线性失真。对带有强记忆效应的射频功放进行准确的建模，是进行后续功放预失真线性化[1-2]工作的必要条件。

为了对带有强记忆效应的功放进行精确的非线性建模，学者和工程师们提出了多种方法，主要可以分为两类：基于Volterra级数的模型[3]和神经网络模型[4]。前一类模型包括记忆多项式（MP, Memory Polynomial）模型[5]、广义记忆多项式（GMP,Generalized Memory Polynomial）模型[6]等。这类模型能直观地刻画功放的各阶非线性失真和记忆效应强度，但当非线性阶数和记忆效应强度增大时，计算量急剧增加。神经网络能够以任意精度逼近任何非线性函数，应用比较多的有反向传播神经网络（BPNN, Back Propagation Neural Network）和径向基函数神经网络（RBFNN, Radial Basis Function Neural Network）。BP神经网络有实数时延神经网络（RVTDNN, Real-Valued Time-Delay Neural Network）模型和改进BP神经网络[7]等。RBF神经网络[8]与BP神经网络相比，收敛速度快，得到了更广泛的应用，其中包括实数时延径向基神经网络（RVTDRBFNN, Real-Valued Time-Delay Radial Basis Function Neural Network）模型和改进型径向基神经网络（MRBFNN, Modified Radial Basis Function Neural Network）模型[9]等。上述神经网络模型没有考虑功放的包络完整性，不包含超前项包络项和滞后包络项[10]，建模精度有待进一步提高。

本文提出了广义改进型径向基函数神经网络（GIRBFNN, Generalized Improved Radial Basis Function Neural Networks）模型，该模型充分考虑了功放的线性记忆效应、非线性记忆效应和超前包络效应以及滞后包络效应，因此能更好地拟合功放的强记忆效应非线性失真。

2 模型设计

2.1 径向基函数神经网络模型

径向基函数神经网络模型的结构如图1所示。输入和输出的非线性关系可以由公式(1)表示：

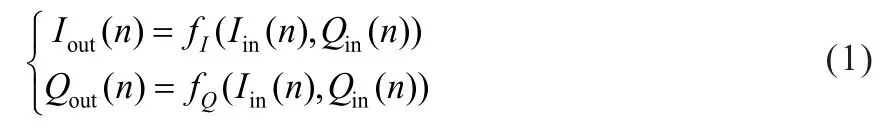
其中，Iin(n)和Qin(n)表示信号的同相和正交分量，Iout(n)和Qout(n)表示输出信号的同相和正交分量，fI(·)和fQ(·)分别表示I路和Q路的非线性变换函数。上述RBF神经网络主要针对弱记忆效应的功放进行建模，不适合应用于强记忆效应功放建模。

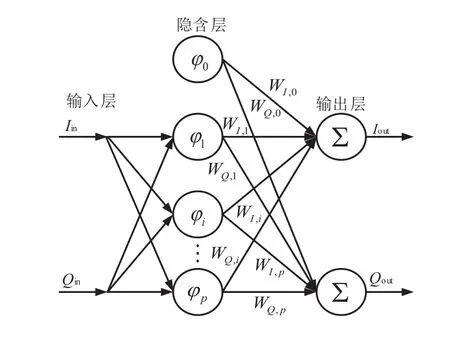
图1 径向基函数神经网络模型结构

2.2 广义改进型径向基函数神经网络模型

广义改进型径向基函数神经网络模型的结构如图2所示：

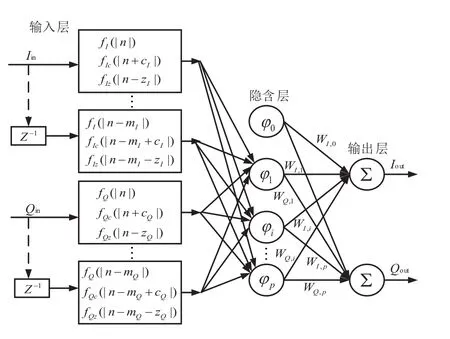
图2 广义改进型径向基神经网络模型结构

在传统RBF神经网络的基础上，输入层使用延时抽头，并对每个抽头进行非线性级数展开，同时还在非线性级数展开模块中引入了超前包络项和滞后包络项；隐含层包含P个神经元；输出层有两个神经元，分别代表I、Q两路输出。其中，输入层可表示为：

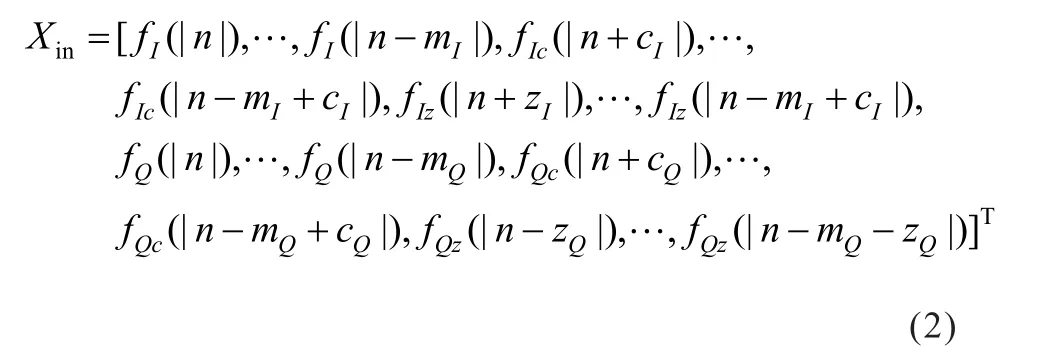
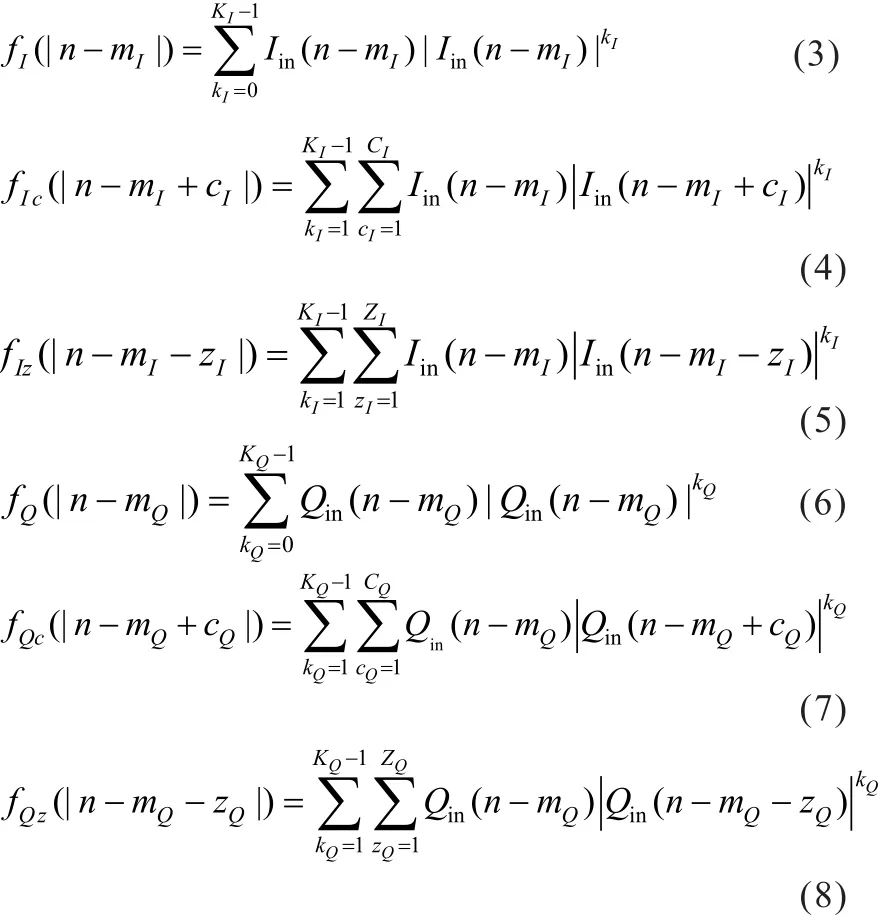
其中，Iin和Qin分别表示输入信号的同相和正交分量，n表示信号采样序列长度，mI和mQ分别表示同相和正交两路信号的记忆深度，kI和kQ分别表示对应抽头的非线性阶数，cI和cQ分别表示I路和Q路的包络超前程度，zI和zQ依次表示I路和Q路的包络滞后程度。

输入层到隐含层用高斯函数作为非线性转换函数，隐含层表达式如下：

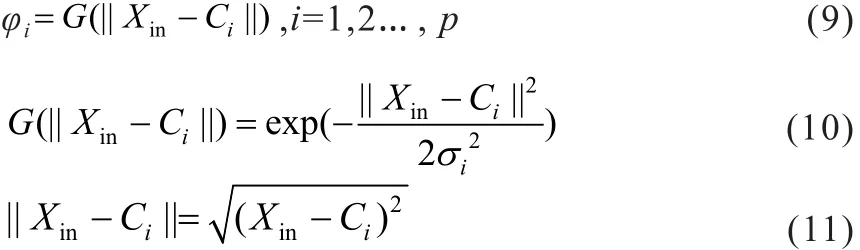
其中，φi为高斯函数，Xin为输入层输入向量，Ci为高斯函数的中心， ||Xin-Ci||为输入向量与高斯函数中心的2-范数，决定拟合曲线的光滑度。

隐含层到输出层的线性变换可以用矩阵运算实现，输出层的表达式如下：

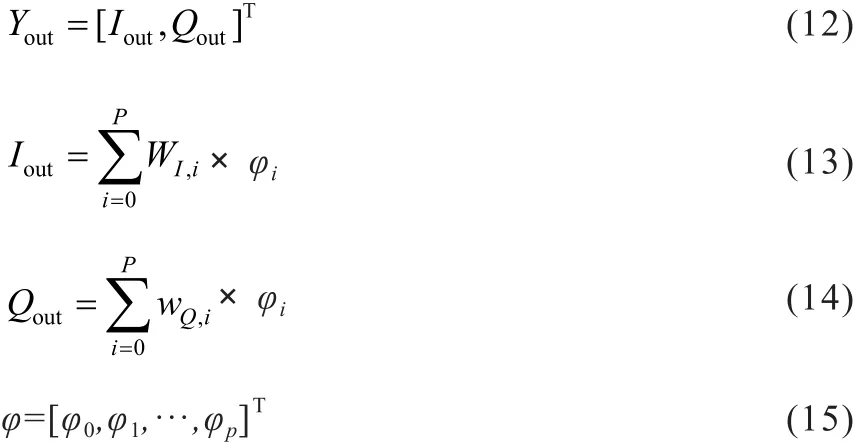
其中，Iout和Qout分别表示I、Q两路的输出，φ为隐含层的神经元，阈值φ0=1， WI和WQ为隐含层到输出层的权值向量。WI和WQ可通过矩阵求伪逆法解出，表达式如式(18)、(19)所示：

至此，本模型的所有参数全部求出，模型架构确立。

3 模型验证与分析

3.1 射频功放特性测试平台

射频功率放大器特性的实验测试平台如图3所示：

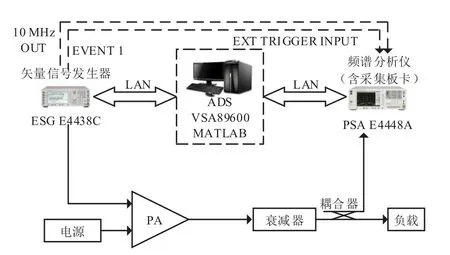
图3 射频功放特性测试平台

首先，利用ADS软件生成信号源，通过的LAN端口将源文件下载到矢量信号发生器中，上变频为射频信号，将射频信号送入带有采集板卡的频谱分析仪，下变频并进行采样，通过安捷伦软件VSA89600A可以得到输入基带信号的“.txt”文件；然后，用射频信号来驱动功率放大器，经过衰减器衰减后，接入频谱仪，通过软件VSA89600A得到输出基带信号的“.txt”文件。最后，对采样获得的输入和输出基带信号依次进行时延估计和对齐等处理。

测试信号是采样率为61.44MSPS的三载波WCDMA信号，信号带宽是15 MHz，PAPR为7；本文选用Doherty射频功率放大器作为测试与建模功放，它的中心频率等于1 900 MHz，工作带宽达到了100 MHz。

3.2 模型验证结果

将输入输出的基带信号送入MATLAB中进行建模，选用10 000个点用于训练GIRBFNN模型，并用另一个周期的10 000个数据点来验证模型精度。通过优化程序确定模型参数，评价标准是归一化均方误差（NMSE, Normalized Mean Squared），NMSE表达式如式(20)所示：

其中，ymod(n)是模型的输出数据，ymea(n)是射频功放实测输出数据。计算所得的NMSE的值越小，表示建模精度越高。考虑建模精度和模型复杂度，最终确定的参数为m=mI=mQ=2、k=kI=kQ=3、c=cI=cQ=2及z=zI=zQ=1。

表1将GIRBFNN模型、RBFNN模型、RVTDRBFNN模型、MRBFNN模型以及GMP模型等四种模型进行了比较，由表1可知，GIRBFNN模型的建模精度最高，其NMSE达到了-41.251 2 dB，这说明了GIRBFNN模型在时域的优势。

参考表1提供的GIRBFNN模型的相关参数，此时GIRBFNN模型拟合的AM/AM和AM/PM特性曲线如图4所示，由图4可知GIRBFNN模型在功率域也能很好地模拟功放特性。

图4 广义改进型径向基函数神经网络模型拟合的射频功放特性曲线图

为了更加清楚地比较几种模型在频域的特性，本文将采用文献[11]提供的方法，分别将几种模型模拟由记忆效应主导的残余频谱的能力进行了对比。方法如图5所示，在被测的射频功放或其行为模型的输入前端端级联一个无记忆多项式预失真器，由此能够更好地比较各模型对记忆效应的仿真结果。

表1 五种模型的NMSE比较

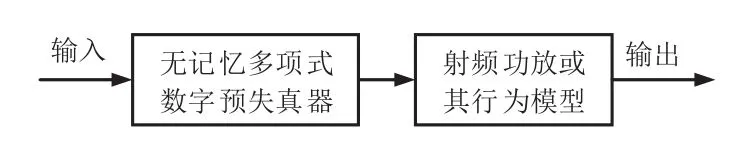
图5 基于无记忆预失真器的射频功率放大器或功放行为模型验证方法框图

过无记忆多项式预失真器，去除射频功放或其行为模型的静态非线性后，残余频谱如图6所示：

图6 多种行为模型输出的残余频谱与功放实测输出残余频谱的比较

由图6可以看出，GIRBFNN模型的残余频谱与实测的功放输出值最为接近。GMP、RVTDRBFNN和MRBFNN三种模型的残余频谱非常接近，但是和功放实测的残余频谱都存在一定差距。RBFNN模型和实测功放输出的残余频谱差别最大，这是因为RBFNN模型不带有记忆效应。

4 结论

为了提高现有模型的建模精度，本文在径向基函数神经网络模型的基础上，提出了广义改进型径向基函数神经网络模型，并用WCDMA三载波信号对Doherty射频功放进行了实验与验证。通过与GMP、RBFNN、RVTDRBFNN和MRBFNN几种非线性行为模型的比较，证明了本文提出的GIRBFNN模型拟合精度较高，能够在时域、功率域和频域都比较准确地拟合射频功放特性。因此，GIRBFNN模型可以用于对带有强记忆效应的射频功放进行准确的建模，也可以用于后续的数字预失真领域，对射频功放的建模和线性化具有研究与应用价值。

参考文献：

[1]葛维军,朱龙彪. 毫米波功率放大器的预失真线性化改进研究[J]. 电子元件与材料, 2015,34(4)： 87-89.

[2]张远见,胡应添. 一种并发双频段数字预失真技术研究[J]. 移动通信, 2017,41(13)： 61-65.

[3]黄浩,钱骅,熊磊. 面向GSM-R/LTE-R双模基站功放的通用双带Volterra预失真系统模型及算法[J]. 中国铁道科学, 2015,36(1)： 111-118.

[4]南敬昌,周丹,高明明. 基于自适应模糊神经网络的功放预失真新方法[J]. 计算机工程与应用, 2016,52(7)： 100-105.

[5]R N Braithwaite. Digital Predistortion of an RF Power Amplifier Using a Reduced Volterra Series Model With a Memory Polynomial Estimator[J]. IEEE Transactions on Microwave Theory and Techniques, 2017,65(10)： 3613-3623.

[6]S Wang, M A Hussein, O Venard, et al. Optimal sizing of generalized memory polynomial model structure based on Hill-Climbing heuristic[C]//2016 46th European Microwave Conference (EuMC), 2016： 190-193.

[7]陈庆霆,王成华,朱德伟,等. 改进BP神经网络的功放有记忆行为模型[J]. 微波学报, 2012,28(2)： 90-93.

[8]M Isaksson, D Wisell, D Ronnow, Wide-band dynamic modeling of power amplifiers using radial-basis function neural networks[J]. IEEE Transactions on Microwave Theory and Techniques, 2005,53(11)： 3422-3428.

[9]林文韬,刘太君,叶焱,等. 基于改进型径向基函数神经网络的功放线性化[J]. 微波学报, 2015,31(5)： 46-50.

[10]G Xu, T Liu, Y Ye, et al. Generalized Two-Box Cascaded Nonlinear Behavioral Model for Radio Frequency Power Amplifiers With Strong Memory Effects[J]. IEEE Transactions on Microwave Theory and Techniques,2014,62(12)： 2888-2899.

[11]Taijun Liu, S Boumaiza, F M Ghannouchi. Deembedding static nonlinearities and accurately identifying and modeling memory effects in wide-band RF transmitters[J]. IEEE Transactions on Microwave Theory and Techniques, 2005,53(11)： 3578-3587. ★