基于稀疏傅里叶变换的快速捕获方法

张春熹， 李先慕， 高爽

(北京航空航天大学 仪器科学与光电工程学院, 北京 100083)

卫星信号捕获是卫星接收机内基带信号处理的第一步，其目的是完成可见卫星的确认并估算出接收信号码相位和载波频率的粗略值，为跟踪通道提供参数的初始化值。常用的捕获方法有基于时域的串行搜索、基于频域的并行频率搜索和基于频域的并行码相位搜索[1-2]。基于时域的串行搜索方法硬件实现复杂度低，但是其所需运算量大、花费时间长；基于频域的并行频率搜索在载波频率方向上进行并行搜索，而在码相位方向上进行串行搜索，捕获的运算量在载波频率方向减小，缩短了捕获时间；基于频域的并行码相位搜索是目前软件接收机平台中常用的捕获方法，通过快速傅里叶变换(Fast Fourier Transform, FFT)实现在码相位方向上的并行搜索，大幅度提高了卫星信号捕获的速度。

在基于频域的并行搜索方法中，FFT运算是实现卫星信号快速捕获的核心[3-4]，为了改善卫星信号捕获性能，产生了基4FFT和分裂基FFT算法[5-7]，通过优化FFT相关运算的效率，提高了捕获速度；但是这些优化的FFT算法的整体时间复杂度仍然是以点数、点数对数的乘积为渐近上限，在运算时间和捕获性能上并没有明显的改善。

由于卫星的伪随机码具有强自相关性，当本地复制伪码和输入信号的伪码相位接近时才能产生很强的相关值，其余搜索单元的相关值都接近于零以致可以忽略。因此对于某颗卫星的二维搜索而言，捕获的相关值具有稀疏的特性，从而可以将稀疏傅里叶变换(Sparse Fourier Transform, SFT)引入并行搜索过程中。

SFT是由MIT的Hassanieh等[8]于2012年提出，其核心思想是利用信号在频域中的稀疏特性，通过加窗—混叠—重构等步骤实现算法的亚线性处理。近年来，SFT在语音处理、医学成像和通信等领域得到应用[9-10]，而在卫星信号捕获中的应用主要是理论分析及仿真验证。文献[11]提出了利用SFT进行GPS信号捕获的方法，并进行了可行性分析，但是没有给出具体的捕获方案和结果。文献[12-13]提出了一种基于SFT的快速捕获与干扰抑制联合技术，简化了算法中快速傅里叶反变换(Inverse Fast Fourier Transform，IFFT)的计算量，但是没有简化输入信号与本地信号FFT算法的运算量。文献[14]利用SFT实现了GPS信号的快速捕获，并分析了降采样因子对捕获速度的提升，但是其对降采样因子的选取不太合理。

本文通过分析卫星信号捕获中的相关值具有稀疏的特性，在基于频域FFT的并行码相位的基础上，提出了基于SFT的快速捕获方法，利用实测的中频数据通过卫星软件接收机进行了捕获实验的验证，实验结果表明本文方法可以降低捕获运算的复杂度，提高捕获效率。

1 卫星信号捕获过程分析

卫星接收机中的信号捕获是一个三维搜索：卫星号(PRN码)、码相位和载波频率[15]。当本地码和信号的码相位对齐的情况下，并且本地载波频率和输入信号的载波频率接近，才能产生很强的相关值。图1为某颗GPS卫星信号捕获成功时的各个搜索单元上的IFFT结果。很明显，在该卫星的二维搜索范围中出现了一个峰值，其不但明显高于其他各个搜索单元的积分值，而且也超过了捕获门限，可以说明对该卫星的信号已被成功捕获，同时也证明了捕获结果的输出值具有稀疏的特性。

基于FFT的并行码相位捕获方法通过FFT实现频域的循环相关，在码相位空间内实现并行搜索捕获功能，卫星信号捕获的效率得到极大的提高。由于FFT相关软件编程模块已经成熟并广泛应用，基于FFT的并行码相位捕获方法成为卫星软件接收机中常用的捕获方法，其实现原理框图如图2所示。

采用基于频域FFT并行码相位捕获方法，其实现的运算步骤如下：

步骤1将数字中频信号和本地载波发生器输出的正弦载波QNCO和余弦载波INCO混频，分别得到同相I支路信号Im和正交Q支路信号Qm，以I支路为实部、Q支路为虚部得到基带的复信号s(t)。

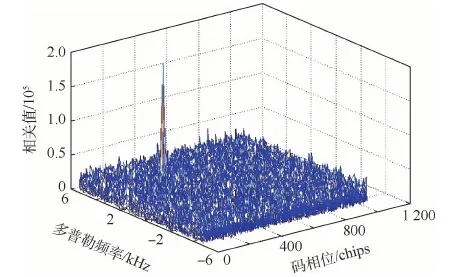
图1 某颗GPS卫星捕获成功结果Fig.1 Successful acquisition result of a GPS satellite

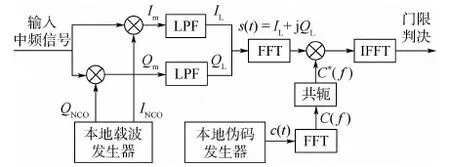
图2 基于FFT的并行码相位捕获方法框图Fig.2 Block diagram of parallel code phase search method based on FFT

步骤2对步骤1中得到的基带复信号s(t)做FFT变换。

步骤3对本地伪码发生器输出的伪码信号c(t)做FFT得到C(f)，并求复数共轭得到C*(f)。

步骤4将步骤2和步骤3得到的结果相乘并做IFFT变换。

步骤5对步骤4得到的IFFT结果取模，得到相关值，对相关值进行门限检测。如果相关值的峰值超过捕获门限值，则捕获到了信号，并得到了信号的码相位和载波频率值；反之，如果相关值的峰值不足够强，信号没有捕获成功，需要重新设置本地载波发生器的频率，重复步骤1～步骤4。

上述方法在完成一个处理(2次FFT和1次IFFT)后能够得到全部伪码相位的结果，所以实现了伪码域的并行处理，而多普勒频率维度的搜索依然是串行的，即每次改变本地载波发生器的频点，则需要完成一次新的处理，即2次FFT、1次IFFT和N次乘加运算。

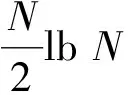
2 稀疏傅里叶变换原理

SFT是利用信号在频域中的稀疏特性，简化FFT运算过程的一种快速有效的算法。在信号具有稀疏性且关键信息处在较大谱峰上时，SFT技术可以在获得与传统FFT相似的频谱分析效果的同时降低其运算复杂度。随着FFT点数的增大，SFT具有的非线性运算复杂度特性将使其在运算方面的优势变得更加明显。

2.1 频域降采样

SFT算法应用了信号在频域中的“稀疏”特性，利用频域降采样减少信号输入长度，提高FFT运算过程的效率。

设x(n)是长度为n的离散序列，X(k)为其频域表示，其时域混叠结果为

(1)

式中：整数B能整除n。令p=n/B，则有

Y(k)=X(kn/B)k∈[0,B-1]

(2)

由式(1)、式(2)可得，时域的混叠对应频域的降采样，反之，时域的降采样引起频域的混叠。图3阐释了这一对应关系。

图3 混叠和降采样示意图Fig.3 Schematic of aliasing and sub-sampling

2.2 稀疏傅里叶变换运算过程

SFT包括频域重排、窗函数滤波、频域降采样、定位、估值及迭代等运算过程，如图4所示。

1) 频域重排。取随机参数σ、τ(τ为奇数)

图4 SFT运算过程Fig.4 Calculation process of SFT

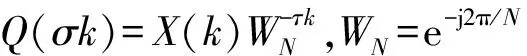
2) 窗函数滤波。将q(n)通过滤波器后有：y(n)=q(n)g(n)。其中，窗函数滤波器通常选用多尔夫-切比雪夫滤波器或者理想的box-car滤波器，其特点满足过渡带陡峭、通带平滑、运算量小和大系数集中。

3) 频域降采样。以因子p将y(n)混叠，对混叠后信号作B点FFT运算得Z(k)=Y(kn/B)。

4) 哈希映射。定义哈希函数和偏移量满足：hσ′(k)=round(σ′kB/n)，oσ′(k)=σ′k-hσ′(k)(n/B)，round(·)表示取整操作。

5) 定位。将Z(k)中最大的谱峰表示为集合J，对于J中的每个元素，令集合H满足条件：H={k∈[n]|hσ′(k)∈J}。

3 基于稀疏傅里叶变换的快速捕获方法分析

3.1 稀疏傅里叶变换优化的捕获方法实现过程

通过第2节对SFT的分析，结合图1中捕获成功的结果，由于伪码信号的强自相关性特性，在FFT相关运算处理过程中，IFFT的变换域具有稀疏的特性，因此可以利用SFT算法对FFT相关过程进行优化。

另外，输入中频信号的频域X(k)并不具有稀疏特性，仅使用加窗—混叠—重构的方法不能使运算效率最大化提升。考虑利用2.1节中“时域的混叠对应频域的降采样”思想对这一过程进行优化。图5为基于SFT的快速捕获方法。

具体算法实现步骤如下：

步骤1将数字中频信号和本地载波发生器输出的正弦和余弦载波混频，得到基带的复信号。

图5 基于SFT的快速捕获方法示意图Fig.5 Schematic of fast acquisition method based on SFT

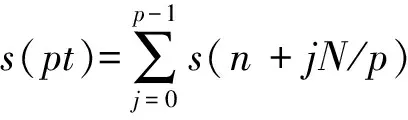
步骤3对混叠信号s(pt)做N/p点FFT。

步骤4对本地伪码做N点FFT，输出结果为C(f)。以因子p对其进行降采样，得C(pf)，取其共轭C*(pf)。

步骤5将步骤3和步骤4的结果相乘，并将乘积做IFFT变换。

步骤6步骤5的IFFT输出结果为混叠结果，对其取模并进行门限判决。得出p个可能的谱峰位置，通过比较这p个坐标的相关值，得到相关值最大的坐标点，其对应的载波频率和码相位即为捕获结果。

3.2 时间复杂度分析

3.1节的基于SFT捕获方法在完成一个处理后能够得到全部伪码相位的结果。步骤2混叠过程需要N次加法；步骤3降采样后N/p点FFT的运算量为(N/2p)lb(N/p)次复数乘法和(N/p)·lb(N/p)次复数加法；步骤4对本地伪码信号的预处理为N点FFT运算量；步骤5相乘操作需要N/p次乘法，稀疏IFFT运算量同N/p点FFT；步骤6鉴别唯一解的运算量为pN/p=N。同基于FFT捕获方法对比，得到单个相关结果，共需要[N+(N/p)(1+lb(N/p))+(N/2)lbN]次复数乘法和[N(1+lbN)+2(N/p)lb(N/p)]次复数加法。其中，本地伪码发生器输出的伪码信号做FFT可以进行预处理，考虑其运算不占用算法时间。则采用FFT和SFT的捕获方法时间复杂度分别为O(NlbN)和O((N/p)lb (N/p))，由此可见基于SFT的快速捕获方法大大降低了相关的运算量，运算量减小到原来算法的plbp倍，且随着数据长度N的增加，其效率提升更加明显。

4 验证实验及分析

为了验证基于SFT的快速捕获方法的效率，利用实测的中频数据对其进行测试。数据中频频率为9.584 MHz，采样频率为38.192 MHz。方法在基于MATLAB的软件接收机上实现[16]，仿真实验对比了基于FFT的并行码相位捕获方法和基于SFT的快速捕获方法的捕获性能。

图6为信号长度T为1 ms，降采样因子p=1、2、4时PRN3卫星捕获结果，表1为捕获实验结果对比。

由图6和表1可以看出，在信号长度为1 ms时，基于FFT的并行码相位捕获方法捕获结果为：伪码相位(采样点)为3.421 2×104，多普勒频率为2.5 kHz，运行时间约为0.26 s。

降采样因子p=2时，检测到的伪码相位(采样点)为1.511 5×104，对应的p=2个可能的偏移位置为N=1.511 5×104、3.421 1×104，分别计算这2个可能偏移位置各自的相关值，N=3.421 1×104点相关值远远大于N=1.511 5×104点的相关值；多普勒频率为2.5 kHz，算法运行时间约为0.14 s，相对于基于FFT的并行码相位捕获方法，程序运行效率提高约1.86倍。

图6 卫星捕获结果(T=1 ms，p=1,2,4)Fig.6 Satellite acquisition results (T=1 ms，p=1,2,4)

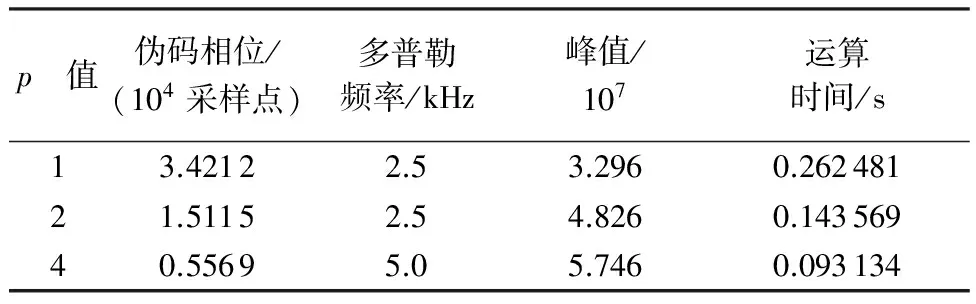
p 值伪码相位/(104采样点)多普勒频率/kHz峰值/107运算时间/s13．42122．53．2960．26248121．51152．54．8260．14356940．55695．05．7460．093134

降采样因子p=4时，检测到的伪码相位(采样点)为0.556 9×104，对应的p=4个可能的偏移位置为N=0.556 9×104、1.511 7×104、2.466 5×104、3.421 3×104，分别计算这4个可能偏移位置各自的相关值，N=3.421 3×104点相关值远远大于其他3个点的相关值；多普勒频率为5.0 kHz，算法运行时间约为0.09 s，但是其多普勒频率估计误差较大，超出多普勒频率搜索步长。

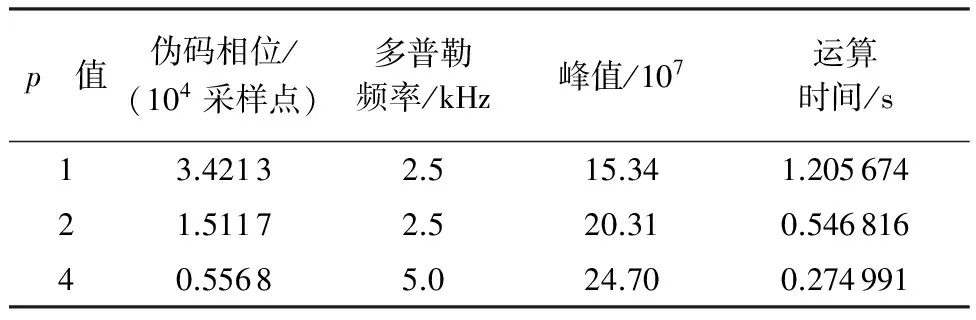
为了验证运算效率随着数据长度N的增大而提升，图7给出了T=2ms的捕获实验结果，表2为T=2 ms时p=1、2、4的捕获实验结果对比。图8给出了T=5 ms的捕获实验结果，表3为T=5 ms时p=1、2、4的捕获实验结果对比。

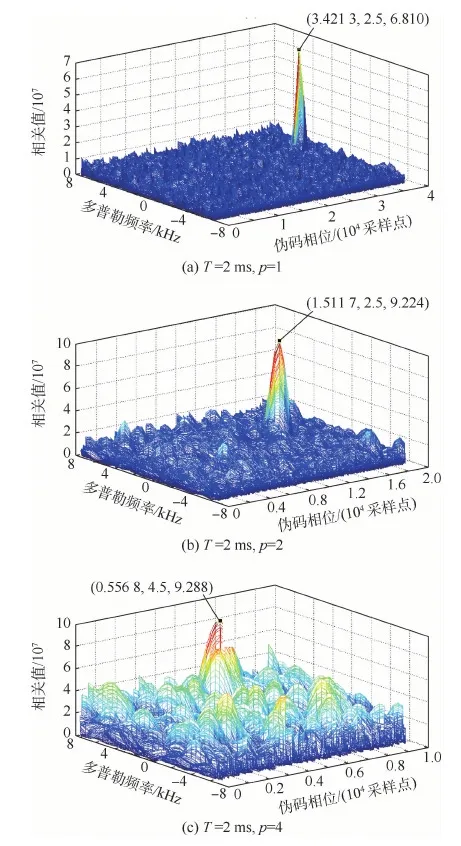
图7 卫星捕获结果(T=2 ms，p=1,2,4)Fig.7 Satellite acquisition results (T=2 ms，p=1,2,4)

由图7、图8和表2、表3可以得出，同T= 1ms时捕获结果分析一致，基于SFT的快速捕获方法可以实现成功捕获。T=2 ms时，程序运行效率相对基于FFT的并行码相位捕获方法提升了2.04倍。T=5 ms时，程序运行效率提升到原来的2.2倍。说明随着数据长度N的增大而运算效率提升更加明显。

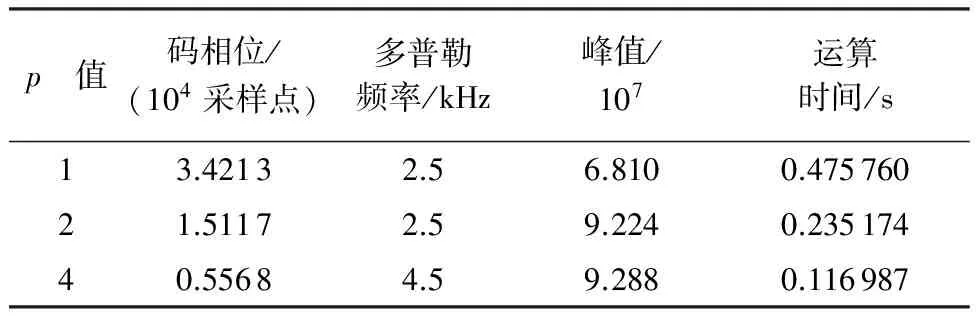
表2 卫星捕获实验结果(T=2 ms)

图8 卫星捕获结果(T=5 ms，p=1,2,4)Fig.8 Satellite acquisition results (T=5 ms，p=1,2,4)

p 值伪码相位/(104采样点)多普勒频率/kHz峰值/107运算时间/s13．42132．515．341．20567421．51172．520．310．54681640．55685．024．700．274991

5 结 论

本文在分析卫星捕获输出相关值结果具有“稀疏”特性的基础上，将稀疏傅里叶变换(SFT)引入基于FFT的并行码相位捕获方法中，提出了基于SFT的快速捕获方法，仿真结果表明：

1) 本文方法可以实现卫星信号的快速捕获，与基于FFT的并行码相位捕获方法相比，算法性能提升到原来的2倍。

2) 当参与运算的信号长度N增大时，算法的运算效率提升更加明显。T=1 ms时，算法运算效率提升约1.86倍；T=2 ms时，算法运算效率提升2.04倍；T=5 ms时，算法运算效率提升2.2倍。

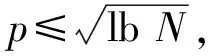
为了更好地验证本文方法，需要利用不同载噪比的中频信号进行验证。

参考文献 (References)

[1] 鲁郁.北斗/GPS双模软件接收机原理与实现技术[M].北京:电子工业出版社,2016:119-157.

LU Y.BDS/GPS dual-mode software receiver principles and realizing[M].Beijing:Publishing House of Electronics Industry,2016:119-157(in Chinese).

[2] 谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009:349-375.

XIE G.Principles of GPS and receiver design[M].Beijing:Publishing House of Electronics Industry,2009:349-375(in Chinese).

[3] COOLEY J W,TUKEY J W.An algorithm for the machine calculation of complex Fourier series[J].Mathematics of Computation,1965,19(90):297-301.

[4] RAO K R,KIM D N,HWANG J J.Fast Fourier transform-algorithms and applications[M].Berlin:Springer,2010:15-40.

[5] AKOPIAN D.Fast FFT based GPS satellite acquisition methods[J].IEE Proceedings:Radar Sonar and Navigation,2005,152(4):277-286.

[6] SPANGENBERG S M,SCOTT I,MCLAUGHLIN S,et al.An FFT-based approach for fast acquisition in spread spectrum communication systems[J].Wireless Personal Communications,2000,13(1-2):27-55.

[7] SAGIRAJU P K,RAJU G V S,AKOPIAN D.Fast acquisition implementation for high sensitivity global positioning systems receivers based on joint and reduced space search[J].IEE Proceedings: Radar Sonar and Navigation,2008,2(5):376-387.

[8] HASSANIEH H, INDYK P,KATABI D,et al.Nearly optimal sparse Fourier transform[C]∥Proceedings of the 44th ACM Symposium on Theory of Computing.New York:ACM,2012:563-578.

[9] 那美丽,周志刚,李霈霈.基于稀疏傅里叶变换的低采样率带宽频谱感知[J].电子技术应用,2015,41(11):85-88.

NA M L,ZHOU Z G,LI P P.Wideband spectrum sensing at low sampling rate based on the sparse Fourier transform[J].Application of Electronic Technique,2015,41(11):85-88(in Chinese).

[10] 王雄.基于稀疏傅里叶变换的水声快速解调算法研究[D].北京:北京理工大学,2015:39-42.

WANG X.Fast demodulation algorithm of underwater acoustic based on the sparse Fourier transform[D].Beijing:Beijing Institute of Technology,2015:39-42(in Chinese).

[11] HASSANIEH H, INDYK P,KATABI D,et al.FASTER GPS via the sparse Fourier transform[C]∥Proceedings of the 18th Annual International Conference on Mobile Computing and Networking.New York:ACM,2012:353-364.

[12] MA Y,BU X Y,HAN H C，et al. Combined algorithm of acquisition and anti-jamming based on SFT[J].Journal of Systems Engineering and Electronics,2015,26(3):431-440.

[13] 龚巧娴.基于SFT的快速捕获与干扰抑制联合算法研究[D].北京:北京理工大学,2015:20-32.

GONG Q X.Research on combined algorithm of acquisition and anti-jamming based on SFT[D].Beijing:Beijing Institute of Technology,2015:20-32(in Chinese).

[14] RAO M V G,RATNAM D V.Faster acquisition technique for software-defined GPS receivers[J].Defence Science Journal,2015,65(1):5-11.

[15] PARKINSON B,SPILKER J. Global positioning system: Theory and applications[M].Reston:AIAA,1996:245-325.

[16] BORRE K,AKOS D M,BERTELSEN N.A software-defined GPS and Galileo receiver[M].Berlin:Springer,2007:75-86.