耦合哈密顿系统的时间序列分析

2018-05-03赵红菊

价值工程 2018年14期

摘要：在研究许多物理模型问题中，人们对系统的具体结构知之甚少，甚至往往不知道其动力学规律，而只是测得与系统性质有关的某一变量随时间变化的数据，这就是所谓时间序列或信号。这被测得的变量可以是系统的状态变量之一，如细胞膜的内外电位差或振动系统沿某一方向的位移，但也可能并不是系统的状态变量而是与系统状态有关的某一变量，如医院里对人从体表测得的脉搏、心电图、脑电图、胃电图、心音和肺音都是如此。在这种情况下，如何由这种时间序列确定系统的运动性质和特征呢？人们用相空间重构和功率谱的方法来对系统的性质和特征进行分析判断。本文章用这两种方法对倾斜磁场下双势阱中粒子的运动模型做了进一步的分析。

Abstract： In many physical model of the problem， people know little about the specific structure of the system， often do not even know the dynamic rules， but only one related to the nature of the system variables can be measured data changes over time， this is called time series or signal. This is measured variables can is one of the state variables of the system， such as inside and outside of the cell membrane potential difference along a certain direction of displacement or vibration system， but also may not be the state of the system but one related to the system state variables， such as the hospital from the surface to the person pulse， ecg， eeg， electrogastrogram， heart and lung sounds. In this case， how to determine the nature and characteristics of the system by this time series？ The properties and characteristics of the system are analyzed and judged by means of phase space reconstruction and power spectrum. In this paper， the motion model of the particle in the two potential well in the tilted magnetic field is further analyzed.

關键词：时间序列分析；相空间重构；功率谱

Key words： time series analysis；phase space reconstruction；power spectrum

中图分类号：O4-0 文献标识码：A 文章编号：1006-4311（2018）14-0274-04

1 研究背景

目前已有较多的混沌研究方法，但许多方法对于一些内部结构不清楚或不易构造其数学模型的系统来说，都束手无策。惟有相空间重构法可由系统中测出某一单变量的时间序列，并用时间延迟技术重构原系统的动力学特征，从而极大地提高了用物理实验理解复杂系统的能力，而且它具有技术上的简便性和数据的可获取性[1]。虽然许多研究人员可以肯定混沌吸引子是某些随机运动的根本原因，但他们更希望能从实验数据中明确证明简单混沌吸引子的存在，即如何看得见它。然而通常的试验并不能记录一个系统的所有方面，而仅仅是其中的少数方面，一般只能得到一维的标量信号，人们遇到的首要任务是如何根据有限的数据“重构”吸引子。Takens指出，系统中任一分量的演化都是由与之相互作用着的其他分量所决定的。因此，这些相关分量的信息就隐含在任一分量的发展过程之中。Packard等人提出的时间延迟思想，能重构出观测到的动力学系统的相空间，这对于不能直接测量深层的自变量而仅仅知道一组单变量时间序列的研究人员来说，也有了研究系统的动力行为的可能。假设在某动力系统中，唯一可观察到的是单变量时间序列x（t），为了研究这个时间序列的动力模型，可以重构相空间。这个时间序列过去的性态含有现在状态的信息，这个信息可以表示为维数为m的时延向量：

2 相空间重构

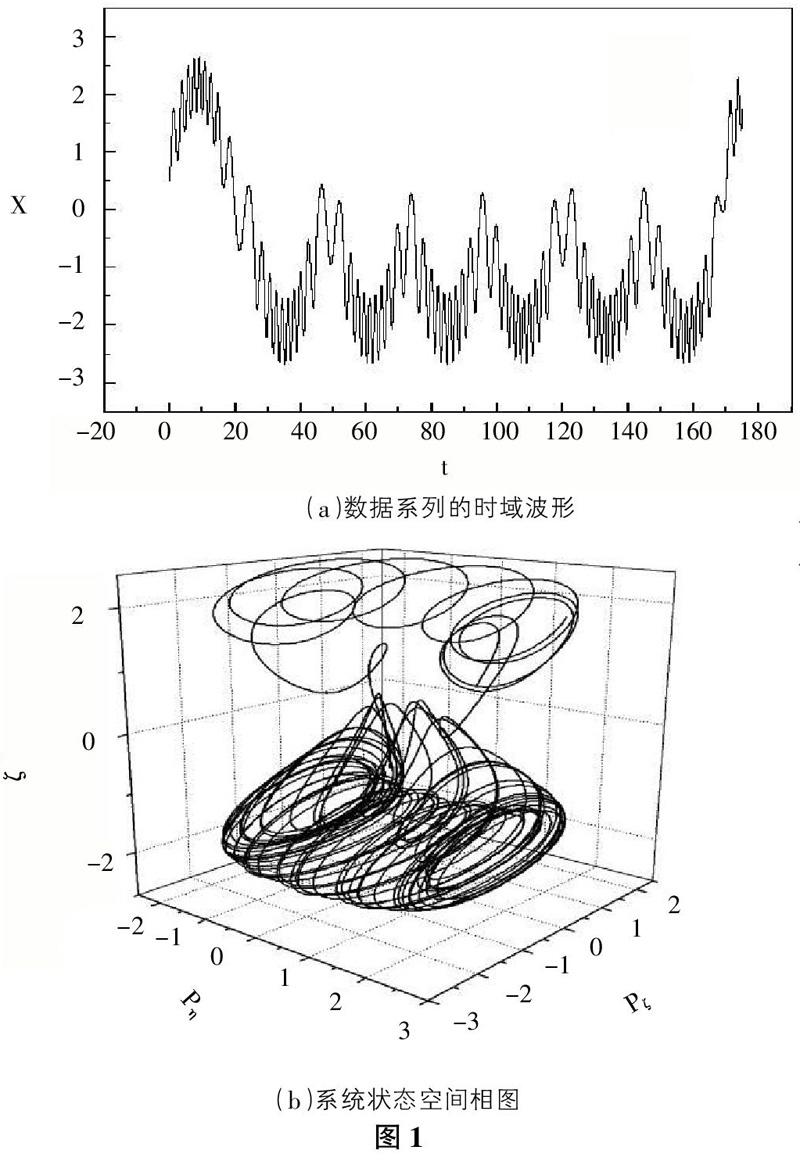
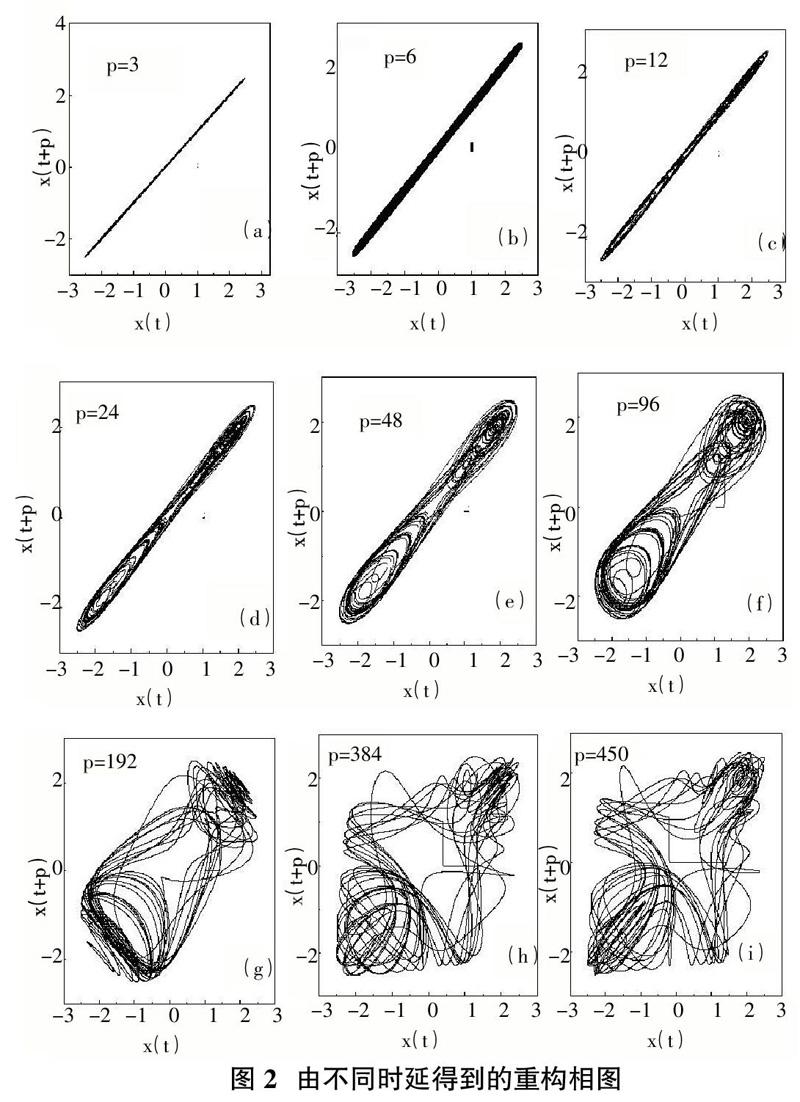
相空间重构可把具有混沌特性的时间序列重建为一种低阶非线性动力学系统，它是非线性时间序列分析的重要步骤。重构的质量直接影响到模型的建立和预测，延迟时间T和嵌入维数m的选择是相空间重构的两个重要参数。对所研究系统我们选择角度等于65度，参数a=c=1，同样选取初始条件p1=0.5，p2=1.2，q1=1.2，q2=0.5来重构它的相空间。从方程中得到一时间序列q2，其中q2的波形和原相图如图1 所示。由图1中（a）可以看出，它是一个具有随机性的非周期信号。该系统的状态空间相图如图1（b）所示，从状态空间相图可看出此方程的解属于混沌状态。选取p从3到450分别作为重构时延进行二维相空间重构，画出部分相图如图2所示。由图2可以看出，当p取96时与原相图具有良好的逼近性。把原相图与重构图做比较（图3），我们得知尽管重构变换使得运动相图形状、大小发生了变化，但运动相图许多根本的动力特性并没有改变，仍然是混沌的。

3 功率谱分析

用功率谱的方法对时间序列进行分析，判断粒子的运动状态随耦合系数改变所做的变化，并与庞加莱截面法的判断结果比较。对一个变量x的分析[3]，首先自然是直接观察其x-t曲线的表现。如果此曲线是规则地周而复始，则系统的运动是周期的：周期的具有一个相等的极大（或极小）值时，则系统是做一周期（1P）运动（基频振荡）；周期地有两个不同的极大（或极小）值时，则系统是做二周期（2P）运动（分频）……。但是如果x-t曲线是杂乱无章或非周期性的，则系统的运动既可能是混沌，也可能是噪声，还可能是准周期运动或有噪声作本底的规则运动。因此，如果x-t曲线是非周期时，我们便无法简单地由此曲线确定系统运动的性质。谱分析一直是分析振动的一种很有效的方法，根据傅立叶定理，任何一个周期为T的周期運动x（t）都可以展开成傅立叶级数：

所以功率谱的分析对于时间序列来说，通常作为研究混沌运动的一种简便有效的工具，系统运动的非周期性可以通过时间序列的功率谱表现出来。这里我们选择q2分量来验证，如图3所示，对应于不同角度所做的功率谱图。横坐标为频率f，纵坐标为频谱F（）。无耦合（角度为0时），各个振子在做相互独立的运动，系统是可积的，运动是规则的，两个振子的振幅随时间变化也是围绕0点周期振荡的，其功率谱就会展示无噪声背景的（如右列图a），在x方向上，粒子以一个频率？棕作简谐振动；x方向的振动在驱动频率？棕处有一较强的功率谱线。一定耦合系数存在时（倾角为4.85度），一个振子的运动受另一个振子的影响，振动而变得不再规则，两个振子的振幅随时间变化均为不规则的。此时运动是非周期的，其功率谱展示了连续的宽带特征，如图右列（图b-c），该谱在低频段有明显离散的峰，在？棕处产生了较宽的连续的频率响应，所以粒子的运动不再是规则的，出现了一定的扩散，粒子趋向混沌运动；同时，x方向的功率谱的频率数量大大增加。这种非线性还破坏了系统哈密顿量的周期性。这个噪声状的功率谱是混沌系统的本质特征。图d在附近有两个较强的功率谱线，同时存在着另外几个较弱的功率谱线，这表明此时粒子的运动是准周期的。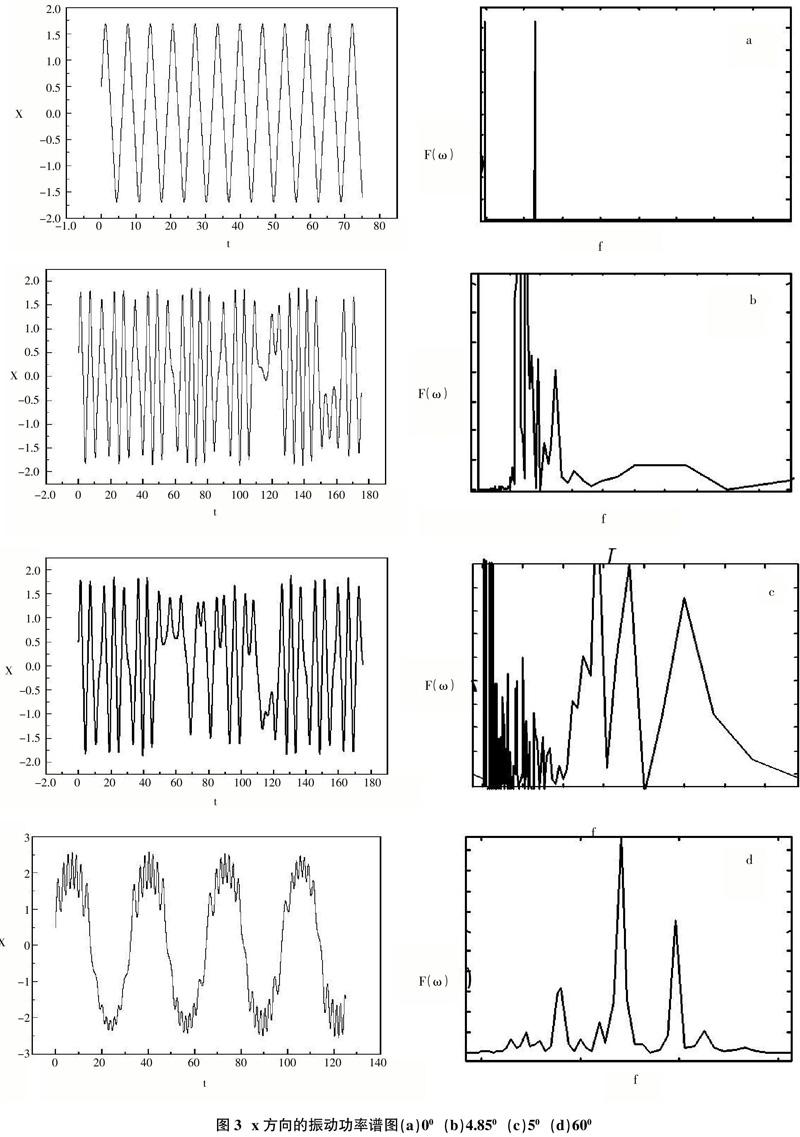

通过上述功率谱的分析，我们可以判断出粒子运动行为随着耦合系数的改变所作的变化。随着倾角的增大，粒子在阱中的运动状态转换为规则—不规则—规则。所得结果与用庞加莱截面方法[1]的判断结果一致，这说明了我们所做出的判断是正确的。功率谱分析方法的优点是只要测出系统中某一个时间序列，而不必测得系统的原模型，就可对它就进行分析判断。

4 总结

综上所述，相空间重构和功率谱分析方法都是利用测得的时间序列来分析系统的运动特征[4]。这两种方法都是利用时间序列对系统进行了分析，分析结果与原系统的性质和特征相符合。由此得出结论：当只测得系统中某时间序列时，我们就可根据它来分析判断出原系统的基本特征。这对于不能直接测量深层的自变量而仅仅知道一组单变量时间序列的系统来说，也有了研究系统动力学行为的可能。