三维服装仿真中人体左右剖面的构造

张妙维， 修 毅

(北京服装学院 计算机信息中心， 北京 100029)

在三维服装仿真人体变形过程中，人体躯干部分形态复杂，变化丰富，研究方法多样。随变形技术的更新和研究的深入，变形效果和交互效率得到提高。

目前，研究较多的一类变形方法是通过扫描大量的人体信息建立人体模型库[1]，将新导入的人体关键信息与模型库中的人体相匹配，将匹配度高的人体经再次合成得到的人体用于新人体[2]。为使精确度和体型覆盖度得到提升，这类研究方法所需人体模型量大，随着研究的展开，模型数量持续增多，过程繁琐。另一类研究较多的是特征驱动变形：根据体型特征将人体分成多个特征区域，针对每个特征区域制定不同的约束和驱动关系[3]；多种变形方法共同驱动复杂的人体变形，增加局部变形调整的灵活性，但变形效果常与实际人体体型规律不符[4]。

孙守迁等[5]提出的参数化人体建模方法中，对腰腹部的变形是基于计算机图形学轴变形技术，将人体模板剖成左右2个部分，并且使用径向变形权重曲线来增加调整的灵活性。该方法建模速度快，但使用的3个人体模板均为标准人体模板，且变形之后的人体模板体型仍在标准体型内。耿玉磊等[4]提出了多因素驱动人体模型变形的方法，可对已有人体进行快速变形。其中对腰围的变型采用的是基于截面环的尺寸驱动算法，这种算法使腰围前后统一变形，变形之后的人体腰腹部突兀，不符合实际人体体型规律。

为得到符合实际人体体型规律的变形，引入一种左右剖面模型算法，该算法沿着肩线和体侧线，横跨人体左右将人体分为前后2部分剖面，可用于对前后2个部分的人体分别进行变形。在人体解剖学里，将人体分成前后2个部分的平面，称为冠状面，与铅垂轴平行。由于本文引入的这种剖面是与人体相匹配的倾斜曲面，不满足冠状面的定义和性质，因此，本文给引入剖面新的定义，根据其横贯人体左右的性质，称其为左右剖面。获得三维服装仿真人体左右剖面的主要流程包括：扫描并处理人体；获取仿真人体用于构造左右剖面的特征点；确定用于构造左右剖面的二次曲面方程；利用获取的特征点的坐标数据和确定的二次曲面方程，构成非齐次线性方程组求解，获得二次曲面系数；求取左右剖面。

1 左右剖面特征点获取

三维人体模型是数字化三维服装造型与设计技术的基础，模拟出的人体要包含真实人体信息，对其进一步处理时获得的数据才有意义。本文采用三维激光仪，通过非接触人体扫描技术扫描人体，获得stl.格式的点云数据人体模型[6]。

通过扫描获取的人体模型，原始数据处理量大，有干扰信息，因此，需要使用Geomagic Studio逆向建模工程软件对扫描人体数据进行拼合、简化、过滤、三角化等，进行反复修剪、删除、排除体外孤点、降噪、修补以及平滑处理得到可用于仿真的人体模型。

由于obj.文件格式简单、通用，对这种以纯文本形式存储了顶点、法线、纹理坐标和材质信息的模型使用起来方便。通过Geomagic Studio将处理过的扫描得到的stl.格式人体模型数据以obj.格式文件导出。在Visual Studio中，利用Csharp OpenGL图形处理接口，搭建para 3D model仿真系统，导入用于仿真的obj.格式的人体数据，得到仿真人体如图1所示。

图1 仿真人体Fig.1 Simulation body

在该仿真系统中，利用射线求交法手动标识仿真人体上的点，选择肩线和体测线上明显、固定、易测部位的一组点为特征点(包括侧颈点，肩端点，前腋窝点，胸围、腰围、臀围分别与体侧线的交点)进行标识，并获取特征点三维坐标数据，特征点选取情况如图2所示。

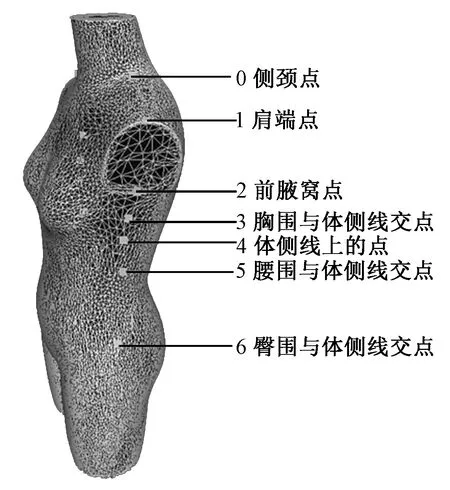
图2 特征点的标注Fig.2 Mark of feature points

2 二次曲面方程确定

在获取了左右剖面特征点的三维坐标数据x,y,z后，需对构成左右剖面的曲面方程类型进行确定。由于获取的特征点三维坐标数据是确定的测量值，构成左右剖面的曲面曲率变化平缓，引入二次曲面构成人体左右剖面的模型为：

Ax2+By2+Cz2+Dxy+Exz+Fyz+

Gx+Hy+Iz+J=0

(1)

式中，A～J为从人体左右剖面二次曲面议程的各项系数。

从解析二次曲面方程[7]分析，如果将1组已知三维坐标的点代入式(1)中，将得到一个多元一次齐次方程组。该方程组只有零解，无法求取二次曲面方程系数。

从人体结构上分析，人体躯干倾斜度整体趋于平缓，仿真人体左右剖面上的三维坐标x、y、z中，z坐标对剖面影响最小，所以去掉z的二阶项，只保留一阶项，经简化后得到二次曲面方程[8]为：

Ax2+By2+Cxy+Dx+Ey+F=z

(2)

将该方程作为左右剖面的模型。

3 非齐次线性方程组求解

使用特征点的三维坐标数据和确定的二阶曲面方程，构成方程组求解方程系数[9]。将标识的特征点(xi,yi,zi)(i=1,2,…,n)三维坐标数据代入式(2)中，由于x、y、z值已知，多元二次曲面方程组构成多元一次方程组，如式(3)所示：

(3)

为求解特征点列和方程组系数[10]，将式(3)(n为特征点个数)转换为矩阵PX=S进行求解，将每行的已知x、y、z值转化为系数矩阵P,S为右边值矩阵,X为反求系数的值，具体表示式为：

(4)

代入不同数量的特征点会导致系数值与方程个数出现以下几种情况：

1)n=6,此时为定解方程组，利用矩阵除法X=S/P可得方程组有唯一解；

2)n<6,此时为奇异方程组，方程组有无数解；

3)n>6,此时为超定方程组，可用最小二乘法求得近似解。

4 左右剖面求取

在标识特征点的过程中，获取的三维坐标值成对出现，由于人体左右面对称使得左右对称特征点的x值互为相反数，y、z相等。将左右对称的特征点代入二次曲面方程，并组成方程组时，所有包含x奇次幂的项都将被抵消。此时式(3)的系数发生变化，求解的不确定因素增加，因此，选择使用仿真人体一侧的特征点，即颈围线的中心点和腰围线的中心点作为新的特征点进行标识，并用这些点的数据组成新的线性方程组求解。在仿真人体上重新取点结果如图3所示。

图3 特征点的重新标注Fig.3 Re-mark of feature points.

选择跨平台、跨编程语言支持的OpenGL作为3-D绘图的API进行3-D仿真，使用面向对象语言的C#语言在Visual Studio、Para 3D Model仿真系统中添加左右剖面的功能。

对指定的特征点进行标识，将指定特征点的三维坐标值中包含x、y项的值存入系数矩阵P中；z的值存放在等号右侧P中；调用数学库中的QR矩阵方法求解PX=S；求出系数A～F的值。

根据非齐次线性方程组的求解原理，求解二阶曲面方程组成的方程组时，当n≥6时方程组有可用解。求解定解方程组、超定方程组获得的二阶曲面方程，呈现的是效果不同的曲面，因此，把求取左右剖面分成标识的特征点数等于6和大于6的2种情况进行分析。

对包含左右剖面的仿真人体进行前、后、左、右观察，当特征点数为6时，仅取最关键的特征点(侧颈点，肩端点，胸围、腰围与体侧线的交点，颈围线、腰围线的中心点)，剖面精确地经过这些特征点，效果良好，其结果如图4所示。

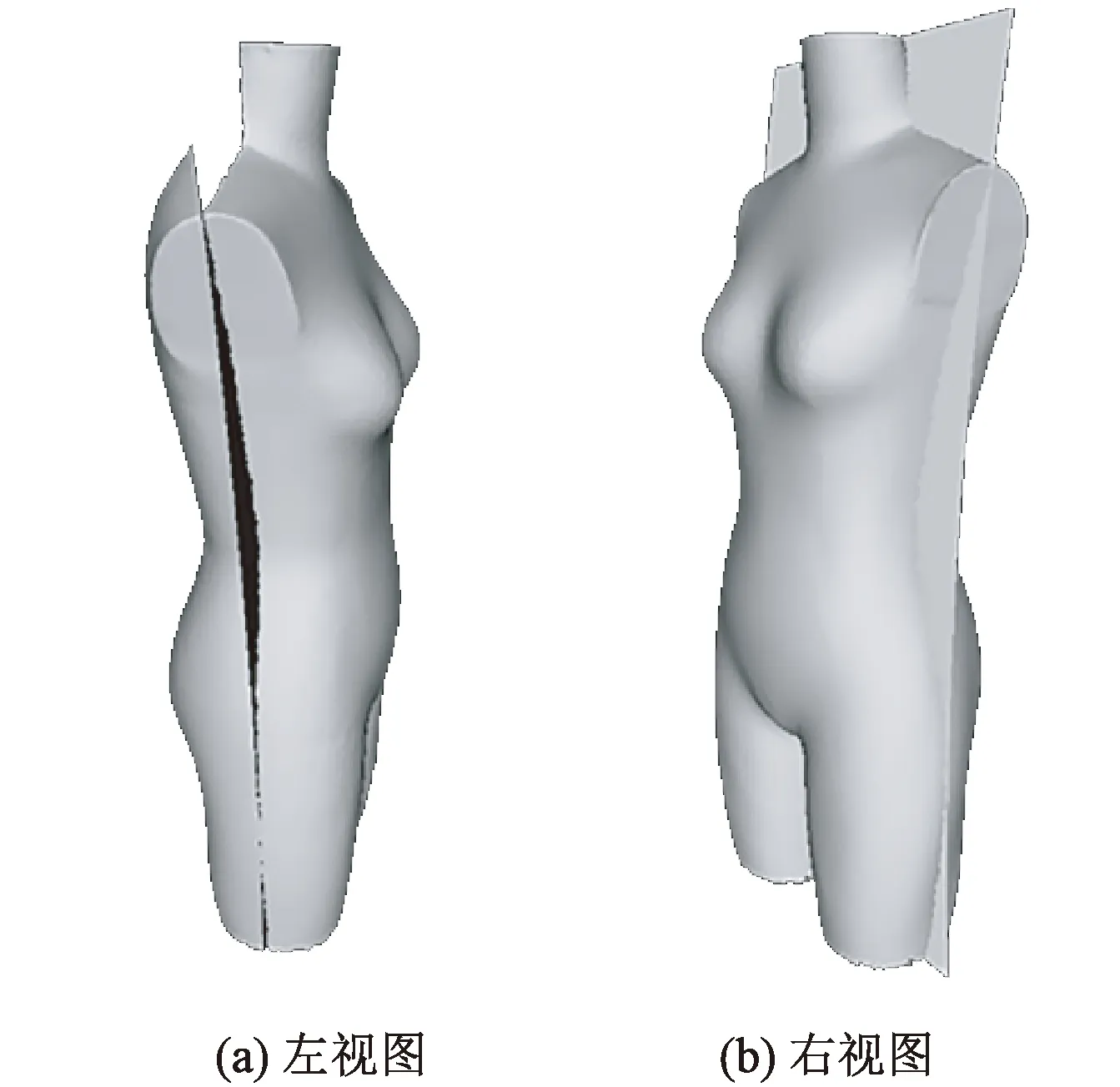
图4 标识点为6的左右剖面Fig.4 Six marked feature points of left-right section. (a) Left view; (b) Right view

当特征点个数为9时，此时标识的点包含人体关键部位的所有特征点(侧颈点，肩端点，前腋窝点，胸围、胸下围、腰围、臀围与体侧线的交点，颈围线、臀围线的中心点)，其结果如图5所示。

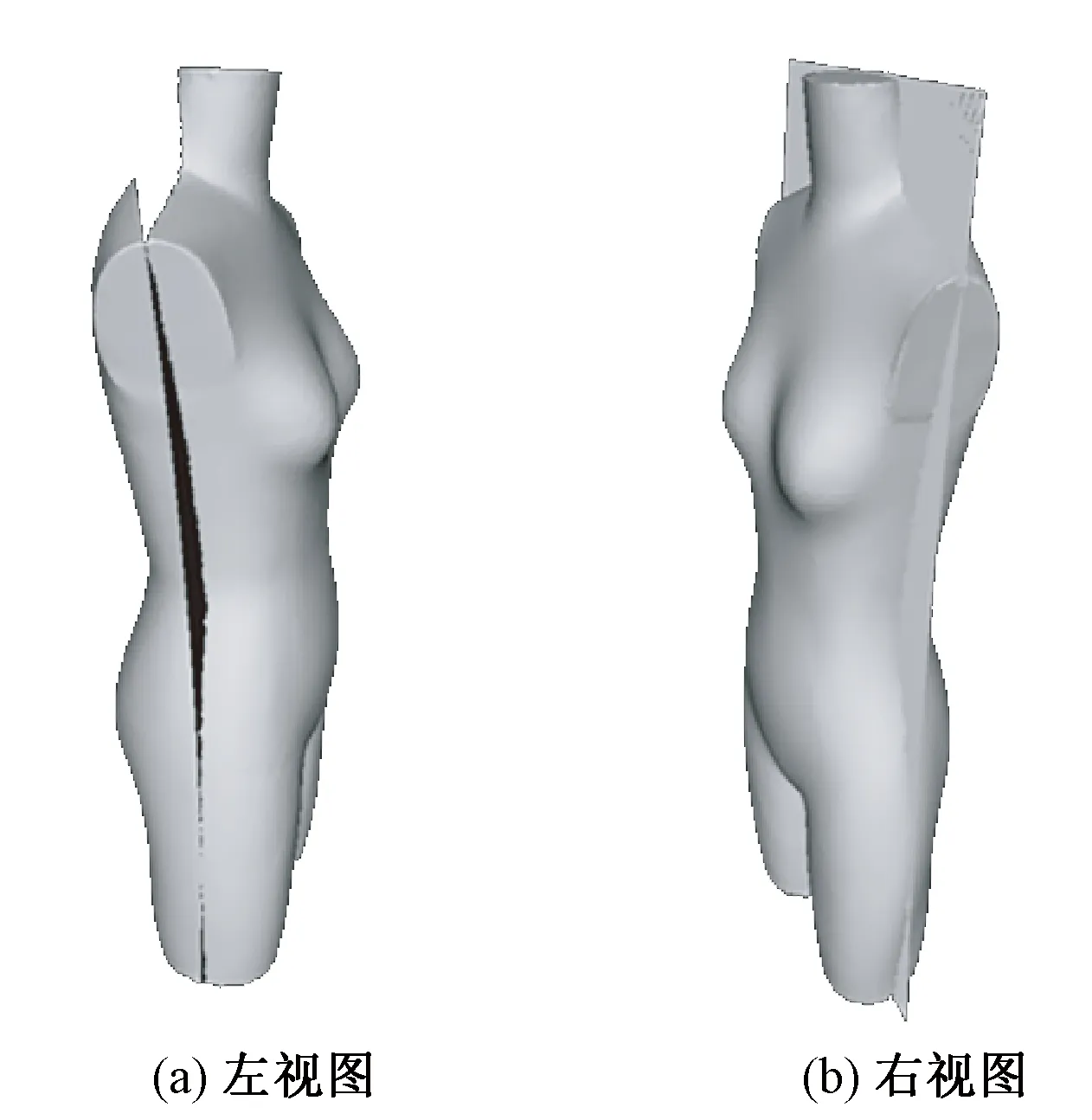
图5 标识点数为9的左右剖面Fig.5 Nine marked feature points of left-right section. (a)Left view; (b)Right view

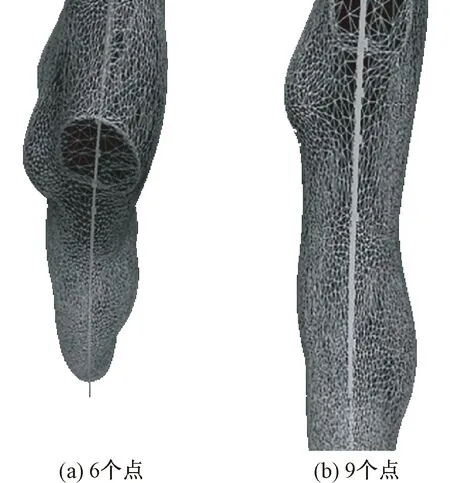
图6 局部细节对比Fig.6 Local detail contrasts.(a) Six points; (b) Nine points

标识不同数量特征点生成的剖面局部细节对比如图6所示。

由图6可知：当标识点个数为6时，剖面全部经特征点；标识点个数为9时剖面大部分经特征点，部分靠近特征点，满足将人体分成前后2个部分的要求。

除对能表征人体测量基准点和测量部位的关键点的标识，即对具有典型代表性的6个和9个特征点的标识外，选取特征点个数为8、10、12、15进行标识，结果如图7所示。在图7(a)～(d)所示4幅剖面展示图中，随标识点的增多非特征点标识的个数也随之增加，剖面对肩线和体侧线上一般点的标识也具有适用性，可满足将仿真人体很好地分成前后2个部分的要求。

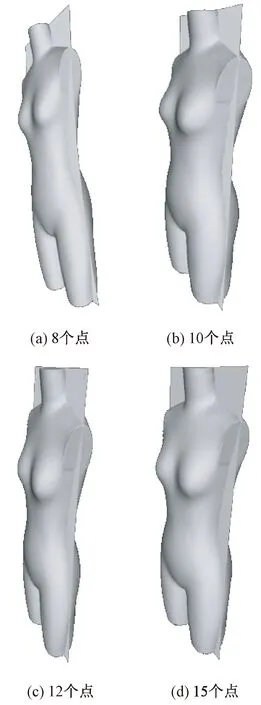
图7 标识实例Fig.7 Mark of examples. (a) Eight points; (b) Ten points ; (c) Twelve points; (d) Fifteen points

5 结束语

在构造空间曲面时，经常采用插值算法和拟合算法，但需要具有一组分布在曲面空间上的数据点作为这些算法的输入数据。在构造人体左右剖面时，由于通过三维扫描只能获取仿真人体表面点的数据，仅已知仿真人体表面肩线和体测线上相关的特征点，无法标识体内点并获取点的三维坐标信息进行利用，因此，本文引入空间二次曲面方程作为左右剖面模型，再利用非齐次方程组求解，最终得到了二次曲面方程，构造出左右剖面。

针对不同时期人体胖瘦脂肪分布规律，将标准人体变形为特殊体型时，人体前后需要进行不同规律变形的目的，生成人体左右变形的基准剖面，通过对肩线和体侧线上点的标识以及形成非齐次线性方程组来求取曲面，该过程简捷、高效。

监测输液正常的关键指标之一: 输液液滴的状态,液滴的快慢代表着输液的不同状态。图2为液滴信号监测示意图。红外对管是检测输液液滴的关键器件。图3是实现输液液滴监测的具体实现电路。

在后续研究中发现，应用左右剖面技术不仅对仿真人体前后区别变形具有良好可用性，还适用于作为服装造型前后部分的基准，对前后相连的统一围线等的分别获取，三维服装到二维平面展平中的中间媒介，三维仿真服装通过轴旋转方式映射到左右剖面上等研究与应用。这些应用为三维服装CAD仿真人体的变形，以及三维服装到二维平面的展平的研究提供了新的思路。

FZXB

参考文献：

[1] WANG C C L.Parameterization and parametric design of mannequins [J]. Computer-Aided Design, 2005, 37(1)：83-98.

[2] CHU C H, TSAI Y T, WANG C C L, et al. Exemplar-based statistical model for semantic parametric design of human body[J]. Computers in Industry, 2010, 61(6):541-549.

[3] 路宁,宁涛,唐荣锡,等.自由变形方法及其在建立尺寸驱动人体模型中的应用[J]. 工程图形学报，2004(1)：76-83.

LU Ning, NING Tao, TANG Rongxi, et al. Dirichlet free-form deformations and their applicationtion dimension driven body model[J]. Journal of Engineering Graphics, 2004(1): 76-83.

[4] 耿玉磊,陆国栋,邓卫燕,等. 面向服装CAD的多因素驱动人体模型变形技术研究[J]. 中国图象图形学报，2009，14(11):2349-2355.

GENG Yulei, LU Guodong, DENG Weiyan, et al.

[5] 孙守迁,徐爱国. 三维服装仿真中的参数化人体建模技术[J]. 纺织学报,2007,28(12):89-93.

SUN Shouqian, XU Aiguo.Study on parameterized mannequin modeling in 3-D garment simulation[J]. Journal of Textile Research, 2007, 28(12): 89-93.

[6] 陈亮,赵曙光,张丽娟,等. 虚拟三维服装展示的发展历史与研究热点[J]. 纺织学报,2011,32(10):153-160.

CHEN Liang, ZHAO Shuguang, ZHANG Lijuan, et al. History and Research hot spot of three-dimensional virtual garment display[J]. Journal of Textile Research, 2011, 32(10): 153-160.

[7] 李二涛,张国煊,曾虹. 基于最小二乘的曲面拟合算法研究[J]. 杭州电子科技大学学报,2009,29(2):48-51.

LI Ertao, ZHANG Guoxuan, ZENG Hong.Algorithm of surface fitting research based on least-squares me-thods[J]. Journal of Hangzhou Dianzi University, 2009, 29(2):48-51.

[8] 霍晓程,李小平. 用最小二乘法拟合曲面方程[J]. 赤峰学院学报(自然科学版),2009,25(6):11-13.

HUO Xiaocheng, LI Xiaoping.Using least squares fitting surface equation[J].Journal of Chifeng Univer-sity (Natural Science Edition),2009, 25(6):11-13.

[9] 张文信,黄阳,潘卫国. 反求工程的一种曲面插值算法[J]. 机电产品开发与创新,2008,21(5):25-27.

ZHANG Wenxin, HUANG Yang, PAN Weiguo. Palletizing robot control system design and implementation[J].Development & Innovation of Machinery & Electrical Products,2008, 21(5):25-27.

[10] 戴中林. 多元线性不定方程的矩阵解法[J]. 四川师范学院学报(自然科学版),2001,22(3):270-273.

DAI Zhonglin.Solution of the multivariate linear indeterminate equation by a matrix[J].Journal of Sichuan Teachers College (Natural Science Edition),2001,22(3):270-273.