基于神经网络的多传感器融合PDR定位方法*

徐龙阳,郑增威,孙 霖*,霍梅梅

(安徽理工大学计算机科学与工程学院,安徽 淮南 232001)

基于位置的信息服务LBS(Location Based Services)依赖于提供可靠、精确、实时的用户位置信息。典型的LBS应用有导航、危险环境救援[1]、外卖服务、位置分享交友等。作为全球最大的定位系统GPS(Global Positioning System)提供的LBS服务,极大地方便了人们的日常生活。人们的大部分时间是在室内环境下度过的,由于该环境下无法有效感测到卫星信号,GPS定位系统并不能提供足够精度的位置信息来满足人们服务需求[2]。因此,有关室内定位技术IPS(Indoor Position Service)已经受到人们普遍关注。各种室内定位技术不断涌现,如红外线定位、超声波定位、WIFI定位[3]、射频识别RFID(Radio Frequency Identification)[4]定位、超宽带UWB(Ultra Wideband)定位[5]等,然而这些定位技术普遍依赖于特定设备支持,各自具有一定局限性,难以实现广泛推广应用。

如今,随着与人们日常生活联系紧密的智能手机广泛普及,越来越多的智能手机内嵌多种传感器(如加速度计、陀螺仪、磁力计等),这些传感器能提供丰富的行人运动信息。行人航位推算PDR(Pedestrian Dead Reckoning)是一种利用手机内嵌多种传感器采集的运动信息进行行人室内定位的技术。该技术通过利用行人初始的位置、行走的距离和方向信息,推算用户在任意时刻的位置信息,无需额外的设备支持。但由于人们行走的随意性、手握手机的方式多样性以及传感器测量的不精确性,使得基于智能手机的定位技术存在误差累积、能量消耗等问题需要解决。

BP神经网络是一种多层的前馈神经网络,具有理论成熟、结构简单,较强的非线性映射能力等优势,是目前应用最广泛的神经网络之一。针对行人行走过程中的随意性运动对步数、步长估计影响,提出一种基于BP神经网络模型预测行人行走距离的方法。为降低传感器漂移对方向估计的影响,一种微航向角融合算法被提出,以获得行人行走方向精确估计。结合行人行走的距离预测和方向估计,最终实现行人位置推算。

1 相关工作

行人航位推算(PDR)是目前比较流行的基于智能手机内嵌多种传感器实现定位的技术,PDR算法根据加速度计、陀螺仪、磁力计等惯性传感器采集的数据实现:步数检测,步长估计,方向估计,在已知行人初始位置的情况下,能够计算行人在任意时刻的位置[6]。步数检测和步长估计可以通过加速度计数据和相应的步长公式完成,方向估计利用陀螺仪、磁力计或一些融合算法如卡尔曼滤波KF(Kalman Filter)等[7]计算得到。近些年来,国内外学者对该技术进行大量研究。Huang Baoqi等人[8]用低通滤波(Low-pass filter)来处理传感器采集的数据,减少短时间的干扰和偏差,并根据垂直角速度生成的步态循环特征进行步数有效检测,无视手机放置姿态的影响,一种基于零速度更新ZUPT(Zero Velocity Updata)的偏差校准算法被用来校准垂直加速度和水平角速度,从而得到精确的步长计算和方向估计。Tian Zengshan等人[9]通过三轴加速度计采集的数据进行有效步数检测、不同人的步长估计以及扩展的卡尔曼滤波EKF(Extended Kalman filter)融合加速度计、陀螺仪及磁力计计算的角度来估算行人的行走方向,实现精确、可靠、持续的定位追踪。

也有一些学者将机器学习模型引用到PDR算法中,用来提高定位精度,如Qian Jiuchao等人[10]根据行人的不同运动状态提出一种自适应步长的估计算法,并将主成分分析PCA(Principal Component Analysis)应用到加速度在水平面上的分量得到行人行走的方向,从而降低了不同的手机姿态对行人行走的方向的影响。为消除手机里传感器的漂移影响,室内地图和粒子滤波PF(Particle Filter)被使用,从而保证了定位的精度和可靠性。Zhou Baoding等人[11]将行人的行走过程中的几个特殊地点的活动如:拐弯、乘电梯、走楼梯等组成一个活动序列,形成一个室内路径网络,定位时用隐马尔科夫模型HMM(Hidden Markov Model)匹配室内路径网络,得到几个最有可能的地点,最终实现用户位置估计。

此外,一些融合定位技术被提出,单纯的PDR定位技术由于误差累积和不精确的传感器测量存在,影响定位精度。融合定位技术能有效降低PDR技术的累积误差,常见的融合定位技术有WIFI[12]、地磁[13]、室内地图[14]以及地标[15]等,融合定位技术的应用提高了定位精度,但也增加了额外的定位成本。

针对基于加速度计采集的传感器数据进行步数检测、步长估计,本文将BP神经网络模型引入PDR算法中,用加速度计采集的原始数据和对应的移动距离数据训练BP神经网络,将训练好的网络模型预测行人的移动距离,以降低传统PDR算法里不精确的步数检测、步长估计计算行人移动距离带来的误差。根据行人行走步伐的连续性特点和同一采样周期传感器输出之间的相关性,提出一种微航向角融合的方向估计算法,通过将当前采样周期陀螺仪、磁力计计算出的方向角和前一采样周期的方向角进行微航向角融合,获得行人行走方向的精确估算。

2 多传感器融合PDR定位方法

2.1 方法概述

本文的定位方法流程如图1所示,由行人移动距离预测、移动方向估计、用户定位三部分组成,第1部分通过手机内嵌的加速度计采集的加速度数据和对应的真实移动距离数据构成训练样本来训练BP神经网络模型,网络模型训练好后,再用测试样本测试已训练好的网络模型,得到行人移动距离的预测。第2部分利用当前采样周期的陀螺仪、磁力计采集的传感器数据计算行人行走的方向角和前一采样周期的方向角经过提出的微航向角融合算法处理,得到行人精确的航向。第3部分结合前两个部分得到的行人移动距离和方向,实现用户室内位置的推算。

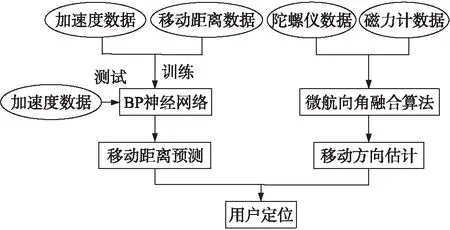
图1 定位方法流程图

2.2 坐标系转换

行人航位推算里因用户不同的手机放置方式和使用习惯会产生一些倾斜角,为消除手机倾斜角的影响,需要周期性的将智能手机坐标系转换到地球坐标系。地球坐标系是以地理经纬度为坐标进行位置确定的绝对坐标系ACS(Absolute Coordinate System),它的X轴为沿地球表面水平向东,Y轴为沿地球表面水平向北,Z轴则为垂直于地球表面向外指向天空。智能手机坐标系则是以用户身上手机为基准的相对坐标系RCS(Relative Coordinate System),其x轴指向手机屏幕的右端,y轴指向屏幕上端,z轴垂直于手机屏幕。图2中,智能手机坐标系Oxyz通过分别绕x、y、z轴旋转角度θ、φ、φ转换到地球坐标系OXYZ。

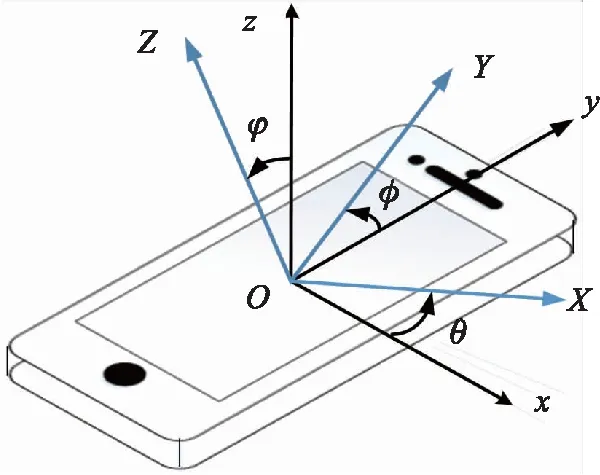
图2 智能手机坐标系及转换

坐标系转换过程中一个代表性方法是欧拉角[16],该方法以一定旋转顺序得到3个单轴旋转矩阵如下:

(3)

式中:θt是t时刻绕x轴旋转的角度,称为俯仰角,φt是t时刻绕y轴旋转的角度,称为横滚角,φt是t时刻绕z轴旋转的角度,称为航向角,3个单轴旋转矩阵相乘得到最终的旋转矩阵Rt如下:

(4)

(5)

2.3 基于神经网络的行走距离预测模型

BP神经网络是一种前馈神经网络,理论发展比较成熟,是目前人工神经网络里应用最广泛的算法之一[17]。本文里BP神经网络模型结构如图3所示,分为三层的网络结构,即输入层、隐层和输出层。输入层输入是第is内三轴加速度计在x、y、z轴上采集的原始加速度数据和对应的行人真实移动距离数据Si,输出层输出每秒移动距离预测值,隐层的神经元数目用试触法确定合适的神经元个数。

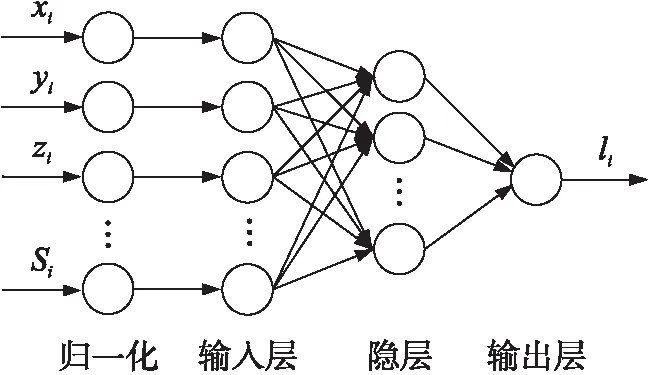
图3 BP神经网络模型

在行人航位推算算法里是通过加速度计数据计算行人的有效步和步长实现行人移动距离计算,因此我们将加速度计采集的三轴数据和真实每秒移动距离数据作为BP神经网络模型的样本数据。考虑到不同的人、不同的手机之间采集的数据差异性影响,对输入数据进行归一化处理,并划分合适数量的训练集和测试集,最终利用训练好的BP神经网络模型来预测行人每秒的移动距离。

为进一步说明该方法的预测精度,本文还进行每秒距离预测对比试验。传统PDR算法距离估计是通过估计行人有效步数和步长得到的,为了方便对比,将步长进行映射,得到第is内行人行走的距离。步长计算方法选择步频和加速度方差模型[18]、步频模型[19]和常数模型[20]:

Li=αfi+βvi+γ

(6)

Li=αfi+β

(7)

Li=c

(8)

在式(6)～式(8)中,fi是第i步的步频,vi是第i步的加速度方差,{α、β、γ}是模型系数,c是固定步长。

行人行走过程中,1 s之内,会有多个有效步,用步长公式计算这些有效步的步长,并进行映射,得到1 s内行人移动的相对距离。考虑到当行人类似直线行走时,1 s内多个有效步的方向变化对映射的移动距离影响不大,因此,1 s内行人移动的相对距离计算为该秒内各个有效步长乘以该步在该秒内所占的时间与该步所花总的时间的比值后的累加,公式如下:

Si′=LjΔtj+Lj+1Δtj+1

(9)

Δtj=ts/tj

(10)

2.4 行人方向估计

本文设计了一种微航向角融合的方向估计MHAF(Micro-Heading Angle Fusion)算法,以获得行人行走方向的精确估计。

2.4.1 算法提出

由于室内环境复杂多变,存在多种干扰源,智能手机内嵌多种惯性传感器灵敏度有限,传感器采集的数据易受干扰。因此,依靠单一传感器采集的数据并不能保证数据真实性,需要多种传感器相互融合、彼此佐证。本文依据行人行走步伐的连续性特点和传感器输出之间的相关性,将3种微航向角:前一采样周期方向角(prev)、当前采样周期陀螺仪获得方向角(gyro)和当前采样周期磁力计得到的方向角(mag),根据区分各类情况、选取可靠的传感器源来融合求解航向角,使航向角更接近行人实际行走的方向。

2.4.2 算法实现

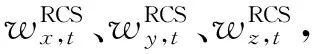
(11)

(12)

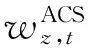
(13)

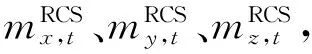
(14)

(15)

微航向角融合(MHAF)算法通过将行人行走过程分类成不同的情况,根据分类结果来选取可靠的传感器源,再利用3种微航向角进行加权融合估算,最终得到行人行走的方向角可靠估算。分类融合关系示意图如图4所示,具体微航向角融合算法如表1所示。

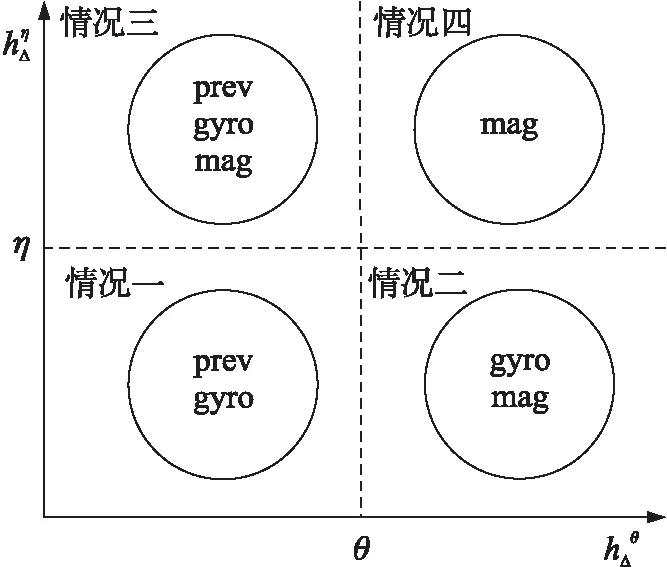
图4 分类选择传感器源示意图

表1 MHAF算法

表1中部分参数如下:

wpgm=(wprev+wmag+wgyro)-1

(16)

wpg=(wprev+wgyro)-1

(17)

wgm=(wgyro+wmag)-1

(18)

(19)

(20)

2.4.3 算法分析

行人直线行走时,由于惯性、连续性特点,前一采样周期的方向角对当前采样周期的参考意义较大,拐弯的时候参考意义相对较小。因此情况一、三中传感器源有prev。传感器输出相似时,可以判断陀螺仪、磁力计相对受干扰较小,反之受干扰较大,又根据陀螺仪适合短时间测量、磁力计适合长时间工作等特点,得出图4所示的分类选择传感器源结果。4种情况对行人实际行走过程的直线和拐弯、传感器输出稳定性有很好地区分,依据不同情况选择合适传感器源,保证方向角计算的可靠性。

2.5 行人轨迹计算

室内环境中,在行人初始位置确定的情况下,任意时刻的位置坐标信息可由行人移动距离和移动方向计算得到:

(21)

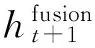
3 实验及评估

3.1 数据集

在本文中,我们使用的数据集来自2015年在日本大阪举行的“UbiComp/ISWC 2015 PDRhallenge”竞赛[21]。数据集统计如表2所示,每条路线上采集的完整数据为一条路线数据。采集数据的智能手机有7种,都内嵌有三轴加速度计、三轴陀螺仪、三轴磁力计及气压计等4种传感器,采样频率分别为200 Hz、200 Hz、50 Hz、40 Hz。由于原始数据集采集并不均匀,我们只使用路线一上采集的数据作为本文的实验数据集(该种情况下的数据量相对较多),设计两种实验方案:方案1是用同一种手机与不同的人之间采集的数据来训练、测试,手机是Nexus5。方案2是用不同的手机和不同的人之间采集的数据来训练、测试。方案1、方案2采集的路线数据量分别是58条、63条。

表2 数据集统计

行人行走路线区域平面图(18 m×17.5 m)如图5所示,包括4个直角,四条边,圆点是行人起始的位置,顺时针行走,再回到起始的位置结束。每一条路线数据采集过程中,由两位志愿subject、operator完成,手机由subject放于胸前采集传感器数据,operator伴随着subject,并通过按日志按钮生成日志数据得到subject每秒移动的相对坐标数据。

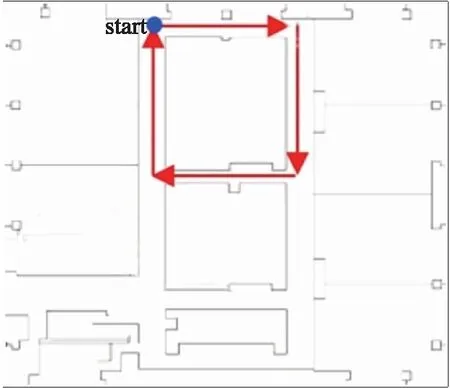
图5 路线行走平面图

3.2 数据预处理

实验前,需要对传感器采集的数据进行归一化预处理,我们将每条路线数据用m×n的二维矩阵表示,每一行数据表示为一个样本。考虑到不同人、不同手机之间差异化的影响,需逐行地对数据进行标准化处理,将每一行数据分别归一化到区间[-1,1]内,当矩阵每一行值都不全相等时,归一化计算公式是:

y=(ymax-ymin)(x-xmin)/(xmax-xmin)+ymin

(22)

当某行的数据全部相同,此时xmax=xmin,除数为0,则y=ymin。其中,x为需要归一化的数据,y是处理后的结果,ymax、ymin默认值为-1和1。

在对比试验中,为除去数据采集过程中的噪声,计算行人有效步数,还需要对加速度数据进行中值滤波处理,滤波区间设置为25。

3.3 实验结果

3.3.1 行人行走距离预测

根据已有数据集设计方案1、方案2,并分别用50、8,55、8条路线数据来训练、测试网络模型。BP神经网络的权值和阈值是随机初始化为[-1,1]区间的随机数,隐层神经元数初始为9个,训练时根据预测的平均误差大小来不断调整至合适的隐层神经元数目,两个方案的预测误差结果如表3、表4所示。

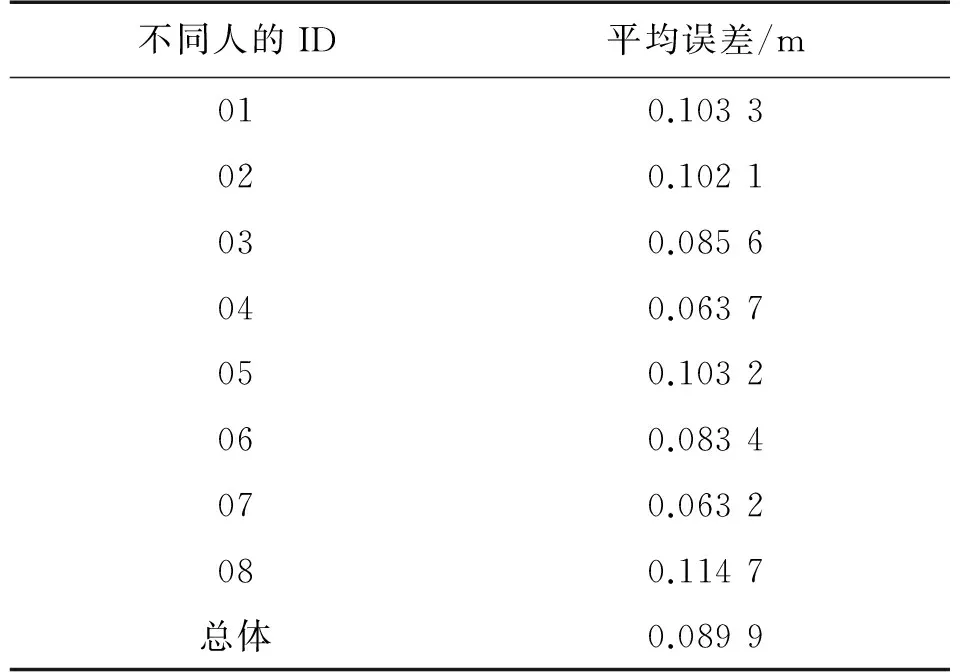
表3 方案1每秒距离预测误差

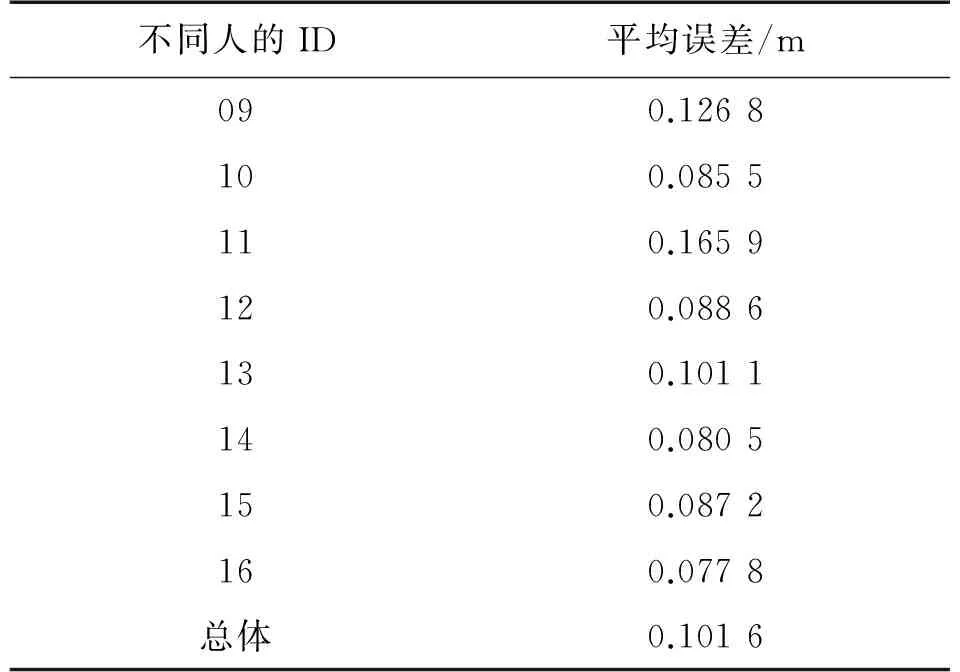
表4 方案2每秒距离预测误差

两种实验方案每秒距离预测结果分析,总体上,两种方案平均误差只有0.092 8 m,其中方案1总体平均误差达到0.089 9 m,方案2是0.1016 m。两个方案里最高平均误差也仅有0.126 8 m,表明了BP神经网络预测方法的可靠性。

从两个方案里选择最接近平均误差的两个人进行对比实验,ID分别是03、12。在整个行走过程中,两个人各自所花时间分别是52 s和64 s,每秒距离预测误差累积分布分别如图6、图7所示。可以看出,方案1里,当预测的每秒距离误差小于0.1 m时,用BP神经网络模型,一共有33 s,占整体时间63.5%,步频和加速度方差模型有14 s,占总体时间26.9%,步频模型有24 s,占整体时间的46.2%,常数模型有28 s,占总体时间53.8%。方案2里,当预测的每秒距离误差小于0.1 m时,用BP神经网络模型,一共有39 s,占整体时间60.1%,步频和加速度方差模型有22 s,占总体时间34.4%,步频模型有10 s,占整体时间的15.6%,常数模型有14 s,占总体时间21.9%,两个方案里提出的BP神经网络模型预测精度都明显高于其他3种步长计算模型。

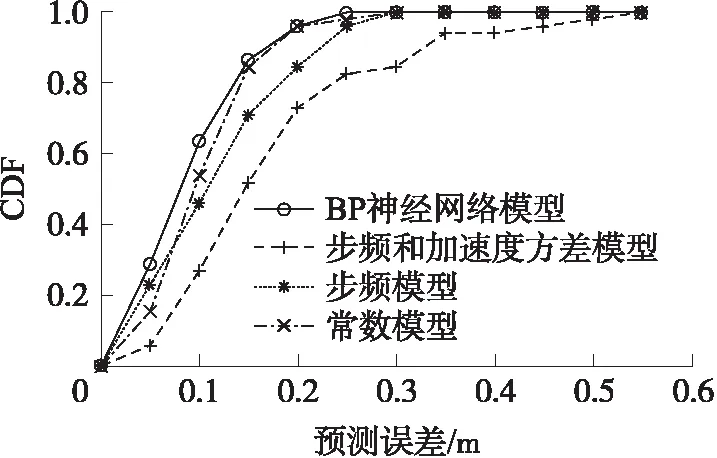
图6 方案1中不同方法每秒距离预测误差的CDF图

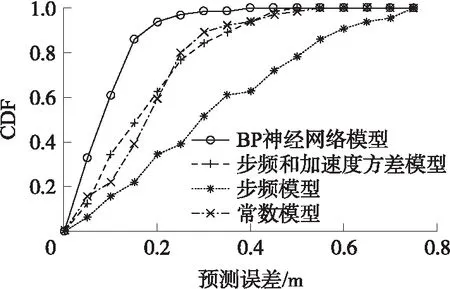
图7 方案2中不同方法每秒距离预测误差CDF图

文中还进行了数据归一化和未归一化预测行人移动距离对比实验,表5、表6分别是不同人之间、不同手机之间实验的预测结果比较,不同人之间用归一化数据预测的行人移动距离的平均误差是0.095 5 m,方差是0.003 1,未归一化数据预测的平均误差是0.105 8 m,方差是0.003 7。不同手机之间用归一化数据预测的平均误差是0.094 m,方差是0.002 5,用未归一化数据预测的平均误差为0.115 m,方差为0.002 9。

由表5、表6可知,用归一化的数据进行行人移动距离预测的总体平均误差和方差都比未用归一化的数据预测精度要高,说明归一化处理数据能够提高预测的精度。

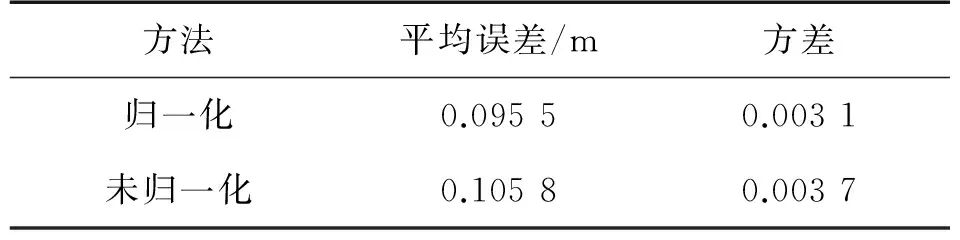
表5 归一化和未归一化在不同人数据集上预测结果比较

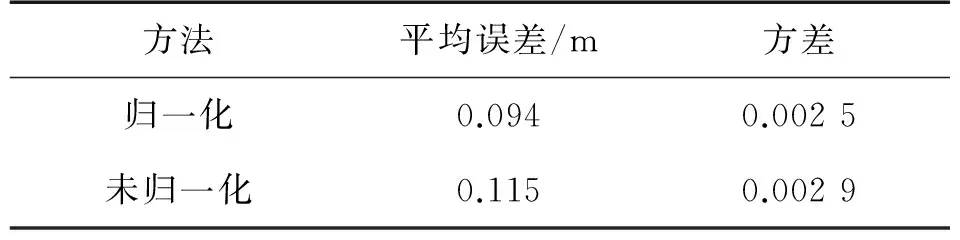
表6 归一化和未归一化在不同手机数据集上预测结果比较

3.3.2 行人行走方向估计

图8是某个人单独使用陀螺仪、磁力计和提出的微航向角融算法来计算行人行走方向与真实方向的对比,方向90°的变化表示一个拐弯。从图8可以看出用陀螺仪计算的方向角有较大的累积误差,尤其是在拐弯处,时间越长,累积误差越大。表明陀螺仪适合短时间的方向计算。用磁力计计算的方向在一些点具有明显的波动性,因为磁力计在该点易受到一些磁性物质、电子设备等物质干扰。提出的微航向角融合算法计算的方向基本与真实的方向一致。表明该算法能够有效降低单独使用陀螺仪、磁力计带来的误差。

图8 不同方法计算的行走方向与真实方向对比

图9是3种不同方法计算的方向与真实方向之间误差,图中出现的波峰表明是在拐弯处,陀螺仪在经历3个拐弯处产生较大累积误差。在整个行走过程中,磁力计在多处受到干扰,出现多个波峰。提出的微航向角融合算法总体上保持较小的波动,平均方向误差仅有9.27°,而陀螺仪是29.28度,磁力计是15.78度,后两者误差都明显高于微航向角融合算法。

图9 不同方法计算的行走方向与真实方向的误差对比

3.3.3 用户定位估计

由行人移动的距离和方向以及初始位置可以推算行人在室内行走的轨迹,移动的距离统一用BP神经网络模型预测得到,方向分别使用陀螺仪、磁力计和提出的微航向角融合算法3种方法来计算。初始位置设置为(0,0)。表7和表8分别是方案1、方案2里使用PDR(BP+陀螺仪)、PDR(BP+磁力计)和PDR(BP+微航向角融合)方法来估计行人行走轨迹的平均定位误差。两个表格一共统计了16个人的定位误差,总体来看,当定位误差在1 m～4 m的范围内,用PDR(BP+微航向角融合)方法定位有12个人,占总人数的75%,而PDR(BP+陀螺仪)方法有7个人,占总人数43.75%,PDR(BP+磁力计)方法仅有4个人,占总人数25%。可以看出,用PDR(BP+微航向角融合)方法的定位误差分布比较集中,大部分集中在1～4 m范围内。

表7 方案1不同方法的定位误差

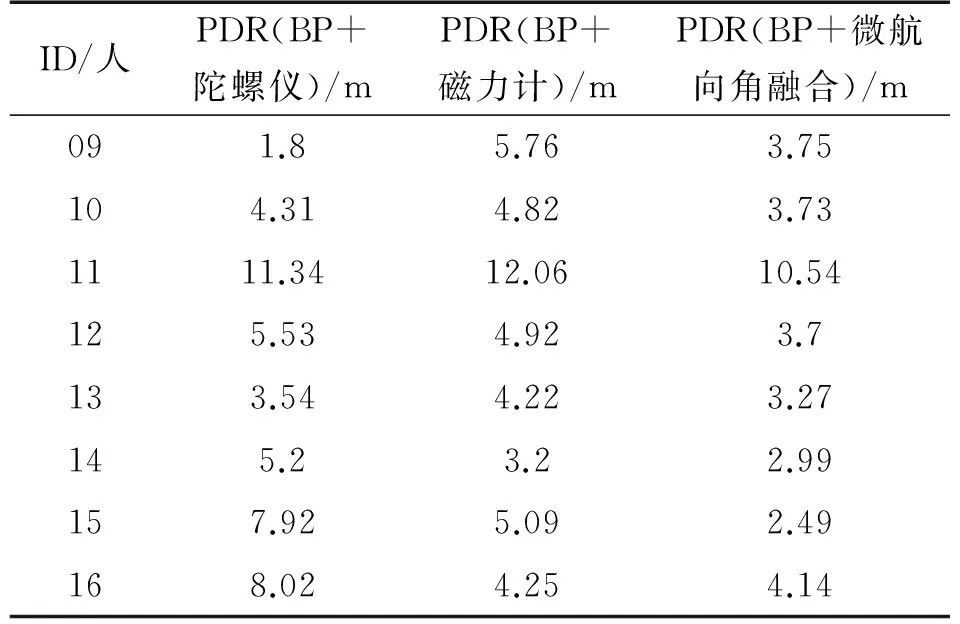
表8 方案2不同方法的定位误差

图10是某个人用不同的定位方法预测的轨迹与真实轨迹对比图,表明通过PDR(BP+陀螺仪)得到的行人行走轨迹具有较大的累积误差,通过PDR(BP+磁力计)磁力计得到的行走轨迹因受到干扰具有一定的波动性偏差,而利用PDR(BP+微航向角融合)得到的行走轨迹与真实轨迹相近,有效弥补了陀螺仪、磁力计计算各自带来的缺陷,实现较好的定位效果。

图11是不同的定位方法的定位误差累积分布图,提出的PDR(BP+微航向角融合)方法定位性能最佳,小于3 m的定位误差达到72.05%,整个行走过程的平均误差仅有2.16 m。

图10 不同的定位方法预测的轨迹与真实轨迹对比

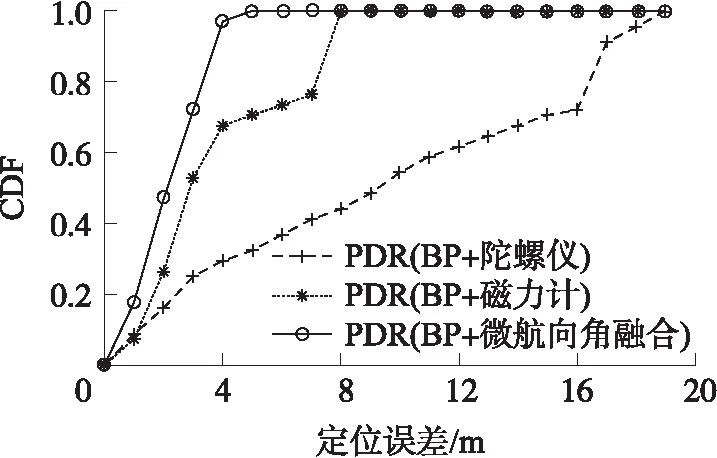
图11 不同定位方法的定位误差CDF图

4 结束语

本文提出一种基于BP神经网络和智能手机内嵌多传感器融合PDR室内定位方法,利用BP神经网络预测行人每秒移动距离,通过提出一种微航向角融合算法估计行人行走方向,最终实现行人位置精确推算。行人行走距离预测实验结果表明,同一种手机、不同的人方案中总体平均误差达到0.089 9 m/s,不同的手机、不同的人方案里是0.101 6 m。两个方案里最高平均误差也仅有0.126 8 m,显示了BP神经网络预测行人移动距离方法的可靠性。每秒移动距离对比实验结果表明,BP神经网络预测的精度明显高于其他3种步长模型计算出的精度。归一化与未归一化数据预测行人行走距离对比实验结果表明,归一化数据能够提高预测精度。方向估计实验结果表明,陀螺仪计算出的方向角在长时间内有较大的累计误差,平均的累积误差达到29.28°,磁力计计算的结果容易受到室内电磁环境的局部干扰,平均误差有15.78°,微航向角融合算法能有效降低传感器漂移影响,得到精确方向估计,平均误差仅有9.27°。行人轨迹预测实验结果表明,通过BP神经网络预测的行人移动距离和微航向角融合方向估算能够实现较好的定位效果,有12个人定位误差保持在1～4 m范围内,占总人数75%,最好的定位精度平均误差仅有2.16 m。

微航向角融合算法虽然在一定程度上弥补了陀螺仪、磁力计各自的缺陷,降低了方向上的误差,但是融合的精度受限于传感器的不精确测量,没有从传感器采集的原始数据上消除测量的误差,因此,未来可以采用先校准传感器的测量误差,然后结合卡尔曼滤波等融合算法计算方向,根本上提高方向的融合精度。

参考文献:

[1] Fink A,Beikirch H. Adding Link Quantity Information to Redundant RF Signal Strength Estimates for Improved Indoor Positioning[C]//Indoor Positioning and Indoor Navigation(IPIN),2012 International Conference on. IEEE,2012:1-6.

[2] 梁韵基,周兴社,於志文,等. 普适环境室内定位系统研究[J]. 计算机科学,2010,37(3):112-116.

[3] 陈斌涛,刘任任,陈益强,等. 动态环境中的WiFi指纹自适应室内定位算法[J]. 传感技术学报,2015,28(5):729-738.

[4] Ni L M,Liu Y,Lau Y C,et al. LANDMARC:Indoor Location Sensing Using Active RFID[C]//IEEE International Conference on Pervasive Computing and Communications. IEEE Computer Society,2003:407.

[5] Gezici S,Tian Z,Giannakis G B,et al. Localization via Ultra-Wideband Radios:A Look at Positioning Aspects for Future Sensor Networks[J]. IEEE Signal Processing Magazine,2005,22(4):70-84.

[6] Harle R. A Survey of Indoor Inertial Positioning Systems for Pedestrians[J]. IEEE Communications Surveys and Tutorials,2013,15(3):1281-1293.

[7] 杨增瑞,段其昌,毛明轩,等. 基于磁场指纹辅助的手机室内定位系统[J]. 传感技术学报,2016,29(9):1441-1448.

[8] Huang B,Qi G,Yang X,et al. Exploiting Cyclic Features of Walking for Pedestrian Dead Reckoning with Unconstrained Smartphones[C]//ACM International Joint Conference. ACM,2016:374-385.

[9] Tian Z,Zhang Y,Zhou M,et al. Pedestrian Dead Reckoning for MARG Navigation Using a Smartphone[J]. Eurasip Journal on Advances in Signal Processing,2014,2014(1):65.

[10] Qian J,Ma J,Ying R,et al. An Improved Indoor Localization Method Using Smartphone Inertial Sensors[C]//International Conference on Indoor Positioning and Indoor Navigation. IEEE,2014:1-7.

[11] Zhou B,Li Q,Mao Q,et al. Activity Sequence-Based Indoor Pedestrian Localization Using Smartphones[J]. IEEE Transactions on Human-Machine Systems,2015,45(5):562-574.

[12] Shen L L,Hui W W S. Improved Pedestrian Dead-Reckoning-Based Indoor Positioning by RSSI-Based Heading Correction[J]. IEEE Sensors Journal,2016,16(21):7762-7773.

[13] Ban R,Kaji K,Hiroi K,et al. Indoor Positioning Method Integrating Pedestrian Dead Reckoning with Magnetic Field and WiFi Fingerprints[C]//Eighth International Conference on Mobile Computing and Ubiquitous Networking. IEEE,2015:167-172.

[14] Yoshimi S,Kanagu K,Mochizuki M,et al. PDR Trajectory Estimation Using Pedestrian-Space Constraints:Real World Evaluations[C]//Adjunct Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2015 ACM International Symposium on Wearable Computers. ACM,2015:1499-1508.

[15] Deng Z A,Wang G,Qin D,et al. Continuous Indoor Positioning Fusing WiFi,Smartphone Sensors and Landmarks[J]. Sensors,2016,16(9):1427.

[16] 高伟,奔粤阳,李倩. 捷联惯性导航系统初始对准技术[M]. 国防工业出版社,2014:2-4.

[17] 郁磊. MATLAB智能算法30个案例分析[M]. 第2版. 北京:北京航空航天大学出版社,2015:237-246.

[18] Cho S Y,Park C G. MEMS Based Pedestrian Navigation System[J]. The Journal of Navigation,2006,59(1):135-153.

[19] Sun Z,Mao X,Tian W,et al. Activity Classification and Dead Reckoning for Pedestrian Navigation with Wearable Sensors[J]. Measurement Science and Technology,2009,20(1):015203.

[20] Cho D K,Min M,Lee U,et al. AutoGait:A Mobile Platform That Accurately Estimates the Distance Walked[C]//IEEE International Conference on Pervasive Computing and Communications. IEEE,2010:116-124.

[21] Kaji K,Abe M,Wang W,et al. UbiComp/ISWC 2015 PDR Challenge Corpus[C]//ACM International Joint Conference on Pervasive and Ubiquitous Computing:Adjunct. ACM,2016:696-704.