基于分段融合的压阻式传感器温度补偿方法*

王 慧,赵国超,金 鑫,宋宇宁

(1.辽宁工程技术大学机械工程学院,辽宁 阜新 123000;2.营口理工学院机械与动力系,辽宁 营口 115014)

通用硅压阻式压力传感器的主要元件为惠斯通桥集成的硅膜片,此类传感器压阻系数与温度直接相关,极易出现温度漂移。对传感器的温度补偿的方法,国内外专家学者也相继开展了众多研究[1-3]。Yuanjiang Li,Yuehua提出了两种改进的PSO算法,并用来解决热电堆传感器的温度补偿问题,通过实验证明了此类方法的有效性及可移植性[4]。Hernandez A,Farah L E提出了一种基于片段线性近似的压阻式压力传感器新型温度补偿算法[5],通过实验证明了补偿算法的有效性,但此方法对非线性段的补偿精度不足。文献[6]利用蚁群算法对RBF神经网络权值阈值进行修正,通过压力传感器补偿实验证明修正后的RBF神经网络补偿效果更好;文献[7]利用遗传算法对BP神经网络进行优化,利用优化的神经网络进行温度补偿实验,弥补了BP神经网络易陷入局部极小的缺陷;文献[8]利用粒子群智能优化算法,将BP神经网络的权值阈值进行优化和修正,提高了BP神经网络的搜索速度并通过压力传感器温度补偿实验验证补偿方法的准确性和有效性,但此类方法对较小漂移的线性段补偿效率不够。

本文提出一种基于粒子群优化RBF神经网络与最小二乘法融合的压阻式传感器温度补偿方法,根据硅压阻式传感器受温度影响变化分段的特性,利用最小二乘法对线性段进行温度补偿;使用粒子群(PSO)算法对RBF神经网络的权值和阈值进行改进,提高RBF神经网络的泛化性,对传感器的非线性段进行温度补偿。

1 压阻式传感器温度补偿模型

压阻式传感器受温度变化的特性,可分为3个不同阶段[9]。随着温度的变化可将传感器的输出函数表示如下:

(1)

处于中温区间[T1,T2]时,传感器随温度呈线性变化,温度漂移造成的影响较小;温度处于低温区间[T0,T1]和高温区间[T2,T3]时,传感器随温度呈非线性变化,温度漂移造成的影响较大。对于线性变化的中温区间段,采用直线最小二乘法进行温度补偿;对于非线性变化的低温、高温区间,采用粒子群优化RBF神经网络进行温度补偿。通过环境温度自适应选择,完成线性段和非线性段温度补偿模型的切换。补偿原理如图1所示。

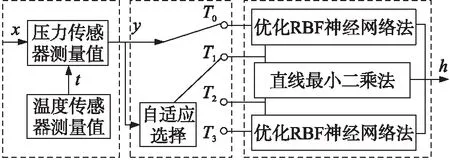
图1 压力传感器温度补偿原理

2 最小二乘法的线性段温度补偿

利用线性方程进行拟合,需要按照一定精度需求自动搜索线性段温度区间,以便得到较宽的拟合区间,实现较大的补偿效率且简化计算难度。通过对给定的一组实验数据(xi,yi),i=1,2,…,n做n次多项式,使得总误差S最小。使用线性方程y=α+βx+e进行拟合,其中α为常数项、β为系数,e为拟合残差。根据文献[10]可知:

(2)

(3)

总误差:

(4)

设线性段温度最初区间为[T1,T2],令[T1,T2]=[T0,T1],对最初区间进行拟合,如果总体误差的最大值Smax比误差设定下极限大,则令T1=T1+τ,其中τ为温度样本间距,对新的区间再次拟合,若依然大于误差设定下极限,则令T2=T2-τ,对所得区间再次拟合,直至拟合总误差Smax满足设定极限要求,得到最终样本训练区间。

3 粒子群优化RBF神经网络的非线性段温度补偿

3.1 RBF神经网络

RBF(径向基函数神经网络)是一种模拟人脑神经网络的三层前馈网络,结构如图2所示。它能以任意精度逼近任意连续函数,具备最佳逼近能力和全局最优特性,且构造容易,训练时间短,对复杂、非线性和不确定性系统具有较强的映射能力[11-12]。

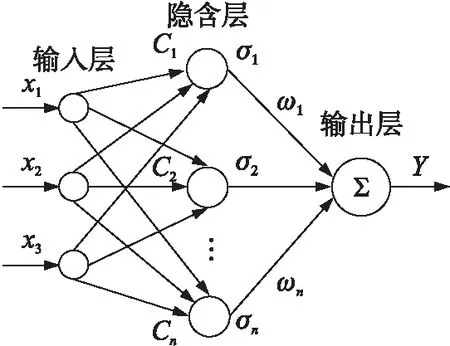
图2 RBF神经网络的结构

RBF神经网络输出层用具有n个输入数据的列向量表示:

X=[x1,x2,…,xn]T

(5)

RBF神经网络隐含层输出为:

(6)

式中:Ci为隐含节点中心;σi为基函数的宽度。

输出层为:

(7)

式中:wi为隐含节点与输出节点的连接权值;bo为输出偏差。

输入层只进行信号输入,不做任何的处理;隐含层采用高斯函数为激活函数,进行非线性变换过程;输出层采用Purelin函数,对隐含层的输出进行线性变换后输出。在RBF神经网络的基本构成中,需要确定的参数有Ci、σi和wi。传统RBF获取这些参数使用的是K-均值聚类算法以及梯度下降两阶段离线算法[13]。这些参数的选取直接影响到RBF神经网络的性能,因此采用粒子群优化(Particle Swarm Optimizer)算法获取隐含节点中心Ci、基函数宽度σi和连接权值wi,进而提高算法泛化能力并发挥粒子群算法全局寻优和提高收敛速度的能力。

3.2 基于粒子群优化算法的RBF神经网络

粒子群算法模拟群鸟寻食的过程,每个鸟就是算法中的粒子即求解问题的可能解。算法搜索模式为速度—位置型,随机初始化一群粒子,每一粒子的位置均代表优化问题的可能最优解,通过不断迭代取得个体和全局最优,更新粒子位置,最终寻得最优解。假设搜索的解空间为N维,存在n个粒子,根据适应函数每次迭代求得种群中每个粒子的位置xi、速度Vi、个体最优Pbest,全局最优Gbest。

取得个体最优和全局最优后,粒子根据式(8)、式(9)更新自己的位置和速度。

(8)

(9)

式中:k为迭代次数;ω为惯性权值,一般在[0.1,0.9]内取值[14];i=1,2,…,n;d=1,2,…,N;加速度因子c1=c2=2[15];随机数r1、r2取值区间为[0,1]。

针对PSO算法中每一粒子都与一个可行解对应,因此采用编码方式对粒子进行编码用来获取隐含节点中心及基函数宽度。编码方式包括隐含层节点的二进制编码;基函数宽度和节点中心的实数编码,结构如图3所示。

图3 编码结构

PSO算法优化RBF神经网络具体方法如下:

①收集样本数据,并对数据进行归一预处理。

②令RBF神经网络的初始化参数变为一列,作为粒子的一组初始化种群。取n个粒子,初始t+1 代,随机粒子的初速度为vi,初位置xi,单个粒子最优值Pi。

③根据式(10)求解粒子适应度。

(10)

④将每个粒子当前适应度fi与历史适应度进行排序,若当前位置比历史位置更好则更新Pbest。

⑤将每个粒子适应度fi与全局中的历史最优位置排序,如果当前优于历史则更新Gbest。

⑥根据RBF神经网络隐含层输出和输出层输出更新粒子位置和速度,并循环(4)～(6)步,直至满足最优条件。

⑦将全局最优的粒子位置和速度进行解码后得到隐含节点中心及基函数宽度。

⑧根据最优的输出结果进行解码,获得神经网络的权值,对神经网络进行训练。

用粒子群算法优化RBF神经网络流程如图4所示。

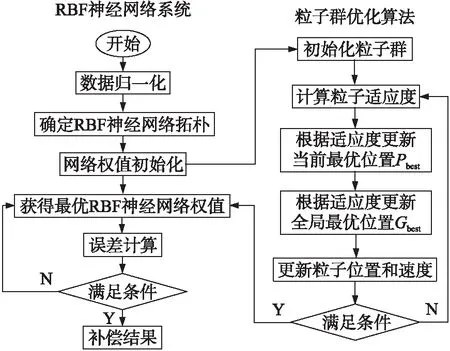
图4 粒子群优化RBF神经网络过程示意

4 温度补偿实验

采用课题组汽车转矩协调控制实验台所用的飞思卡尔24 PC型压力传感器对温度补偿系统进行实验验证,设定温度区间为[-20 ℃,80 ℃],温度变化步长为10 ℃;压力区间为[5 kPa,20 kPa],压力变化步长为 5 kPa。温度补偿前传感器部分数据如表1所示。

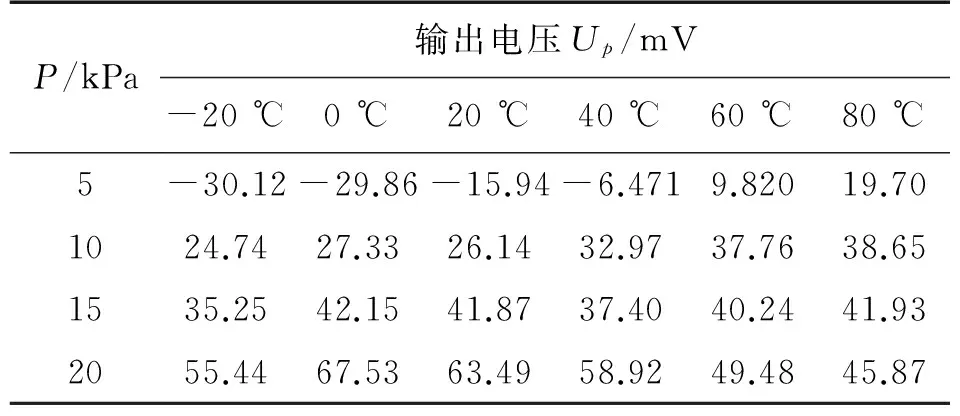
表1 24PC型传感器补偿前实验数据

温度补偿前对不同压力和温度状态下的传感器实际输出电压和测量输出电压进行对比,测量误差拟合曲线如图5所示。

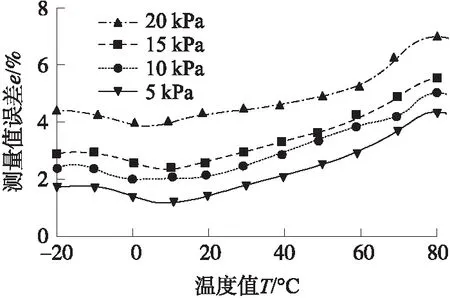
图5 补偿前的传感器测量误差

由图5可以看出,在低温区间[-20 ℃,10 ℃]和高温区间[50 ℃,80 ℃],压力传感器的误差呈现非线性变化趋势;而在中温区间[10 ℃,50 ℃]误差呈线性变化趋势。

针对非线性变化和线性变化区间分别采用PSO优化的RBF神经网络和最小二乘法进行温度补偿实验。用最小二乘法所用的线性拟合方程为[16]:y=1.067 1x-2.631 2;用神经网络进行温度补偿的参数设定如表2所示。

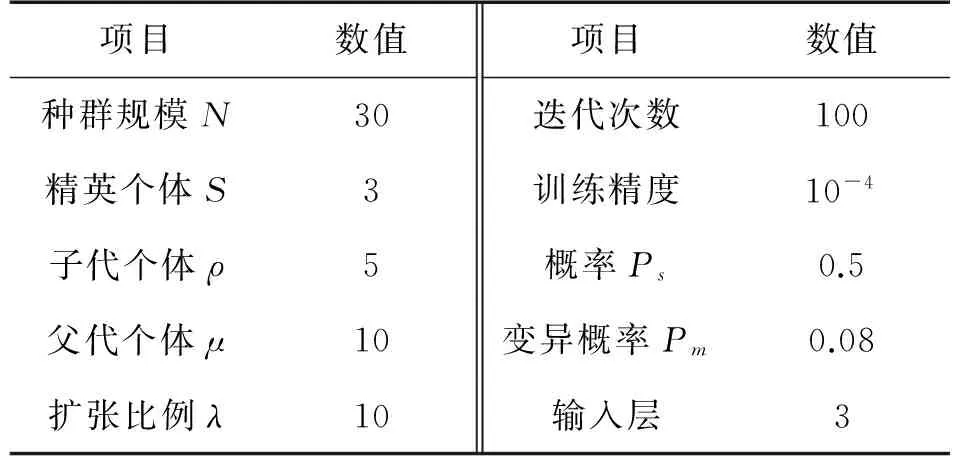
表2 RBF神经网络参数设定

将常规RBF神经网络和PSO优化的RBF神经网络进行对比训练,样本训练曲线如图6所示。

图6 训练曲线

经过100次迭代后,PSO优化的RBF神经网络精度为1.125×10-4,常规RBF神经网络的精度为1.632×10-2;常规RBF神经网络出现局部最优。由此可得,与常规的RBF神经网络相比,PSO优化的RBF神经网络训练精度更高,训练效率更好。

利用PSO优化的RBF神经网络和最小二乘法对该压力传感器进行温度补偿实验,得到补偿后传感器测量误差拟合曲线如图7。

图7 补偿后的传感器测量误差

对比补偿前后传感器误差,利用PSO优化RBF神经网络进行温度补偿后,压力为5 kPa时,传感器的平均误差在0.4%～0.6%之间;压力为10 kPa时,传感器的平均误差在0.3%～0.8%之间;压力为15 kPa时,传感器的平均误差在0.8%～1.4%之间;压力为20 kPa时,传感器的平均误差在0.8%～1.7%之间。较大程度削减温度和压力对传感器的影响,整体补偿效果表现良好。

为证明本文研究方法对传感器非线性变化温度区间补偿的优越性及整体补偿效率,在25 kpa压力下,对该传感器依次采用全局常规RBF神经网络、全局最小二乘法及本文方法进行对比实验。温度补偿效果及所用时间如表3、表4所示。

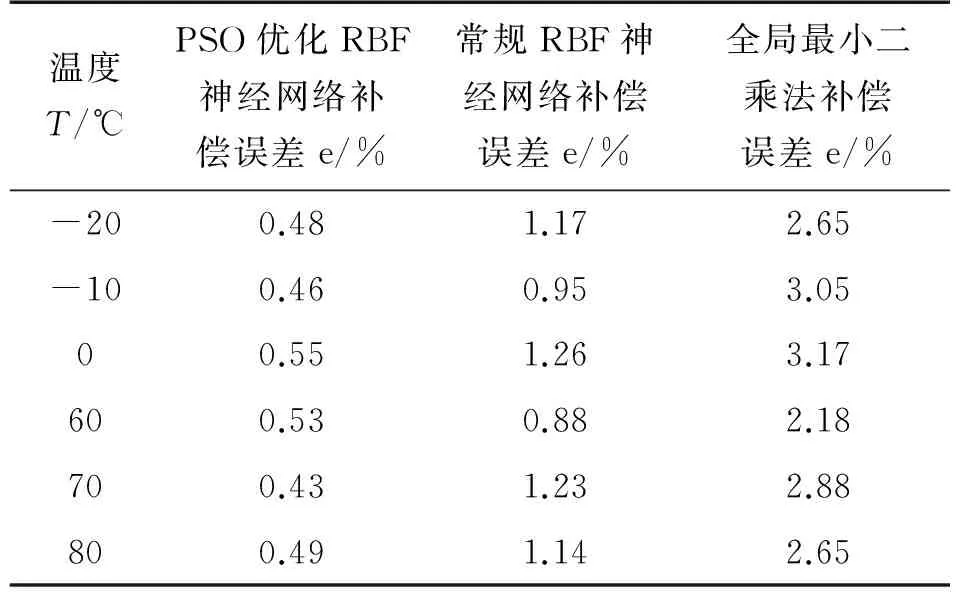
表3 温度补偿效果对比

表4 温度补偿所耗时间

对比3种算法的补偿效果可以发现,在非线性温度区间内,使用最小二乘法进行温度补偿的误差在2%～3%区间;使用常规RBF神经网络进行温度补偿的误差控制在1%范围内;使用PSO优化的RBF神经网络进行温度补偿误差明显小于1%,经过PSO优化后的RBF神经网络对传感器温度补偿效果明显高,有效地抑制了传感器温漂带来的测量误差,提高了测量精度。

从补偿时间上看,本文研究的方法,在吸收最小二乘法线性补偿优势基础上加强了对非线性段的补偿,提高了补偿时间显著优于全局常规RBF神经网络,逊于全局最小二乘法。但综合效率和补偿精度来看,本文方法优于其他两种方法。该方法特点在于利用计算机对算法处理具有较好的性能及充裕的资源,可推广到此类传感器的漂移补偿问题。

5 结论

(1)采用粒子群算法实现常规RBF神经网络权值和阙值的优化,增强了神经网络的泛化能力,避免了局部最优的发生。同时,网络训练速度、精度明显提高,结果波动性和偶然性的发生得到控制。

(2)对比未进行温度补偿的实验测量误差,证明PSO优化RBF神经网络温度补偿模型拟合效果更佳,能有效的控制温度和压力对传感器的影响。

(3)在传感器非线性变化温度区间内,进行3种不同的温度补偿模型对比实验,结果表明:应用本文研究的补偿模型,传感器对温度变化的敏感程度大大降低,整体效果良好,补偿效率增加,满足课题项目对传感器输出数据的精度要求。

参考文献:

[1] 陈韦名,曾喆昭,廖震中,等. 一种湿度传感器温度补偿的非线性校正方法[J]. 传感技术学报,2017,30(5):742-745.

[2] 杨遂军,康国炼,叶树亮. 基于最小二乘支持向量机的硅压阻式传感器温度补偿[J]. 传感技术学报,2016,29(4):500-505.

[3] 王晓,杨祖安,彭碧辉. 改进型RBF神经网络在磁致伸缩液位传感器中的应用[J]. 自动化技术与应用,2015,34(12):5-8,33.

[4] Li Yuanjiang,Li Yuehua,Li Feng,et al. The Research of Temperature Compensation for Thermopile Sensor Based on Improved PSO-BP Algorithm[J]. Mathematical Problems in Engineering.2015.

[5] Hernandez A,Farah L E,Ramirez J. New Thermal Compensation Algorithm for Piezoresistive Pressure Sensors Based on the Linear Approximation by Segments[J]. Mathematical Problems in Engineering,2015,31(4)246-256.

[6] 宋瑞娟. 基于改进RBF神经网络的传感器温度补偿系统研究[J]. 机械强度,2016,38(6):1225-1228.

[7] 彭基伟,吕文华,行鸿彦,等. 基于改进GA-BP神经网络的湿度传感器的温度补偿[J]. 仪器仪表报,2013,34(1):153-160.

[8] 孙艳梅,苗凤娟,陶佰睿. 基于PSO的BP神经网络在压力传感器温度补偿中的应用[J]. 传感技术学报,2014,27(3):342-346.

[9] 行鸿彦,彭基伟,吕文华,等. 一种湿度传感器温度补偿的融合算法[J]. 传感技术学报,2012,25(12):1711-1716.

[10] 孙艳梅. 压阻式压力传感器温度补偿方法研究[D]. 齐齐哈尔:齐齐哈尔大学,2012.

[11] 张小俊,张明路,李小慧. 基于RBF神经网络的电化学CO气体传感器的温度补偿[J]. 传感技术学报,2009,22(1):11-14.

[12] 单亚峰,孙璐,付华,訾海. 基于小波包和RBF神经网络的瓦斯传感器故障诊断[J]. 传感技术学报,2015,28(2):278-283.

[13] 张晓磊,王辉林. 压阻式压力传感器的温度补偿算法研究[J]. 中国农机化学报,2015,36(5):234-236.

[14] 行鸿彦,邹水平,徐伟,等. 基于PSO-BP神经网络的湿度传感器温度补偿[J]. 传感技术学报,2015,28(6):864-869.

[15] 李强,周轲新. 基于PSO-BP算法的压力传感器温度补偿研究[J]. 电子学报,2015,43(2):412-416.

[16] 王慧,宋宇宁. 基于混合优化算法的压力传感器温度补偿[J]. 传感技术学,2016,29(12):1864-1868.