冲击波测试系统中压力传感器的实时动态补偿实现

魏 娟,张志杰,赵晨阳,李岩峰

(中北大学仪器科学与动态测试教育部重点实验室,太原 030051)

一定当量的炸药引爆后,能在极短的时间内释放出大量的能量,产生高温,同时释放大量气体,向周围介质施加高压,接着高压气浪继续向外膨胀并压缩周围空气介质,使其压力、密度、温度等物理量发生突跃式变化,从而形成冲击波[1-2]。冲击波的超压峰值、正压作用时间和比冲量是估计炸药毁伤效果的主要参数[3]。

试验中通常利用冲击波存储测试系统对冲击波信号直接进行采集,但系统中的压力传感器动态响应特性不能满足测试系统的需求,有效带宽不能覆盖信号的频谱。在冲击波信号的陡峭前沿的激励下,在谐振频率点附近信号的幅值大幅度增加,测试数据出现激烈震荡,进而产生较大的动态误差,影响测试精度[4-6]。因此需要对压力传感器及测试系统的动态特性进行补偿,提高传感器的响应速度、降低超调量、扩宽工作频带以达到动态测试需求[7]。

1 动态补偿滤波器设计

1.1 动态补偿原理

在实际测量中,被测信号总是不断变化的,通过测试系统传感器的输出结果来获取、估计被测信号,这就要求传感器能够实时地、无失真地跟踪被测信号的变化过程,因此需要研究传感器的动态响应特性[8]。传感器的动态特性是指传感器对随时间变化的输入量的响应特性。动态特性好的传感器,其输入量随时间变化的曲线与被测量随同一时间变化的曲线一致或近似[9]。实际动态校准系统中,根据“标准”输入信号,观测传感器的响应信号来估计传感器的响应特性。

传感器动态特性补偿的目的是使传感器的有效工作频带能够包含被测信号的所有频谱分量,进而满足动态测试需求。本文采用逆向滤波的方式(如图1),在传感器系统后接补偿滤波器,达到扩宽频带的目的。根据QR分解估计逆向滤波器模型的阶数,改进粒子群(PSO)算法估计滤波器系数,从而得到滤波器传递函数。将所得到的滤波器进行硬件实现,用于实际冲击波测试中,达到实时动态补偿目的。

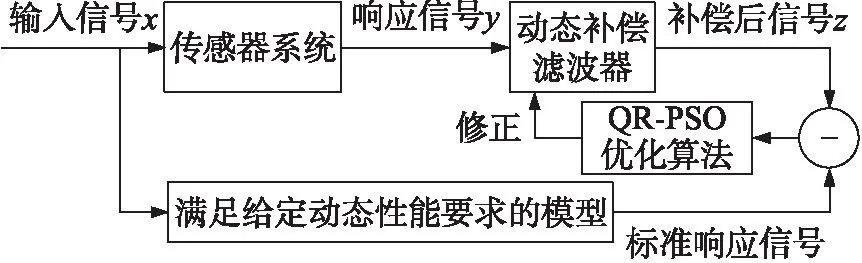
图1 动态补偿原理框图

1.2 算法原理

动态补偿滤波器的模型估计首先需辨识模型阶数。压力传感器系统一般等效为二阶系统,但在试验或实验中,由于输入信号的激励作用,它的输出信号在谐振点处容易发生震荡[10],引入了动态误差。因此以二阶系统作为补偿模型的最终估计偏差较大。

本文以激波管产生的阶跃信号作为“标准”输入信号,对被校准传感器进行激励,由采集电路获取响应数据并进行处理,得到建模所用样本数据。对样本数据进行QR分解,求取残差平方和,判别最优阶数。构建实验数据矩阵D={(u(k),y(k))|k=1,2,…,N}

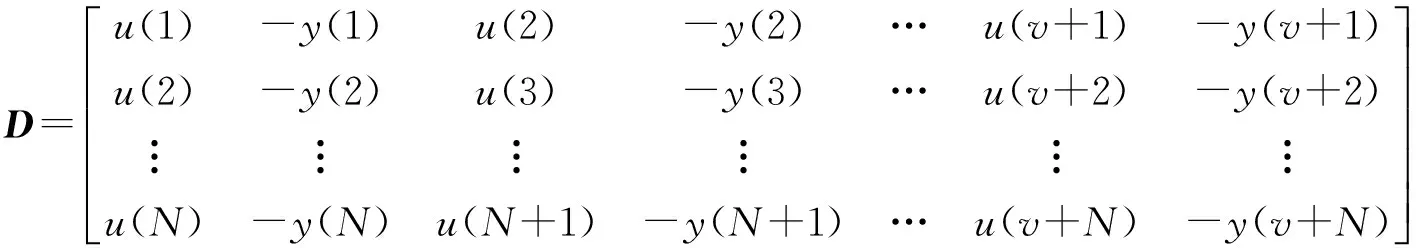
式中:v为待检验的阶数,N为数据长度,对矩阵进行QR分解,可以得到

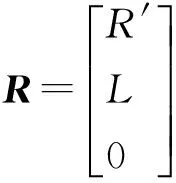
R′是一个m×m维的上三角方阵。计算R′阵对角线偶元素平方和数值即为各阶差分方程模型对应于最小二乘法估计的残差平方和[11]。通过比较各阶模型残差平方和的大小,确定补偿模型适合的阶数。

滤波器的系数由改进粒子群(PSO)算法得到,粒子群算法是一种基于群体智能的全局优化计算技术,具有高精度的稳定性、并行性和全局搜索能力。在此算法中,每个粒子通过不断更正空间方位在D维空间中寻找最佳方案。每个粒子搜寻过程如图2所示。

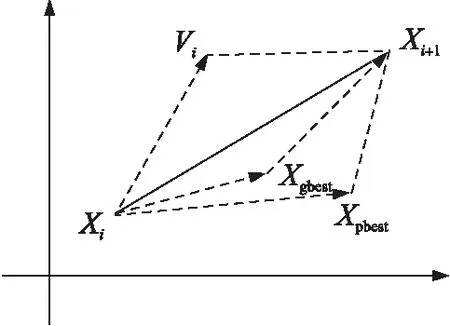
图2 粒子搜寻过程示意图

每个粒子都有独立的位置Xi=(xi1,xi2,…,xiD)和速度Vi=(vi1,vi2,…,viD),并且这两个因素随时间和空间不断变化,各个粒子按照式(1)(2)更新其速度和位置[12]。

vid(n+1)=wvid(n)+c1r1d(n)(pid-xid(n))
+c2r2d(n)(pgd-xid(n))

(1)

xid(n+1)=xid(n)+vid(n+1)

(2)

式中:w为惯性权,c1,c2为加速系数,r1d,r2d为在[0,1]内均匀分布的随机数,n为当前迭代次数。选择合适的惯性权值w使全局和局部搜索之间达到动态平衡后,能够具有较快的收敛速度[13],故本文中选取线性递减权值(LDIW)策略,惯性权值按照式(3)进行更新:

(3)

式中:M为最大允许迭代次数,i为当前的迭代次数。

计算各个粒子的适应值与当前最优位置的适应值进行比较,根据适应度函数的运算结果,在D维空间中不断更新自己的最优位置Pbest=(pi1,pi2,…,piD)和全局最优位置Pg=(pg1,pg2,…,pgD)。本文中适应度函数(式4)采用均方误差值进行比较,具体的优化流程如图3所示。

(4)

式中:yi为预测值,ki是理想输出,N为样本数目。

图3 改进粒子群算法优化过程

1.3 模型搭建

本文建模所用的实验样本数据采样率为2M,选取6 000个点和“理想”阶跃信号构建逆滤波模型,辨识逆向滤波器的阶数和系数。图4为残差平方和随阶数变化示意图,从图中可以明显看出残差平方和在2阶之后明显下降,结合硬件的实现难易程度考虑选取6阶。

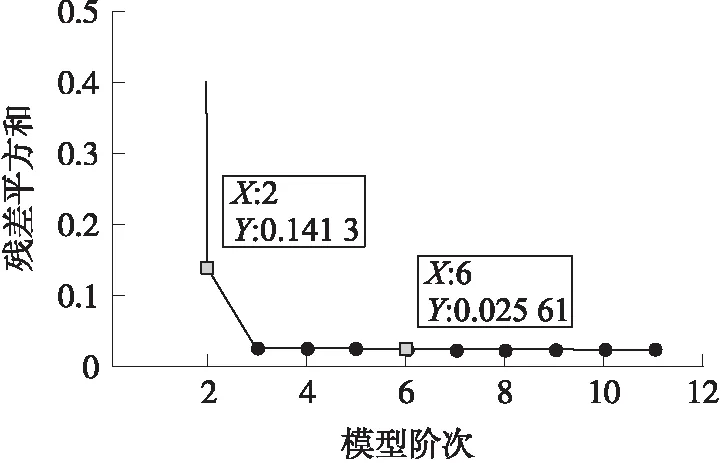
图4 残差平方和随阶数变化示意图

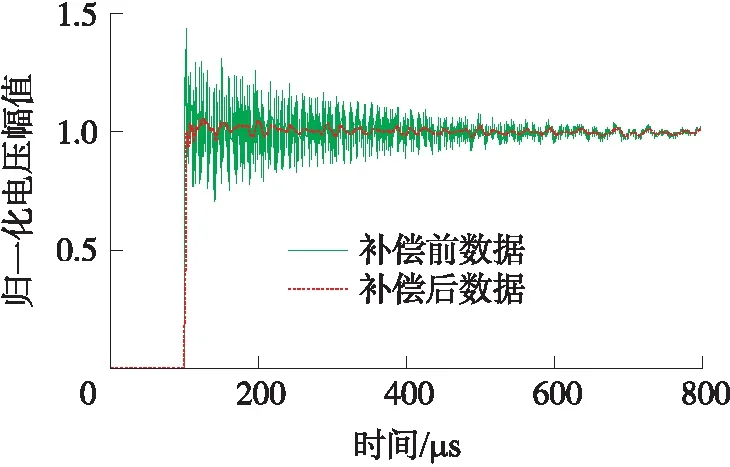
图5 补偿前后信号对比图

在补偿滤波器阶数确定之后,将粒子群训练次数设置为4 000次,初始粒子群个数为40个,数据采样频率为2M,长度为6 000个点,wstart=0.95,wend=0.4,进行训练,得到补偿滤波器的传递函数H(z)和补偿前后信号对比图,如图5所示。从图5可明显看出补偿后信号的超调量降到5%左右,上升时间3 μs,平台压力稳定,补偿效果良好。

H(z)=(0.214 8+0.392 2z-1+0.094 1z-2+0.375 0z-3+

0.205 1z-4+0.147 4z-5)/(2-0.320 3z-1-0.157 1z-2+

0.860 6z-3-0.357 4z-4-0.598 6z-5)

2 IIR数字滤波器量化精度设计

补偿滤波器为IIR递归模型,这样的结构在硬件实现过程中,需要考虑有限字长效应,保证量化后的系统极点都位于单位圆内,满足设计的稳定性[14-15]。

数字滤波器量化精度的设计很大程度上决定了滤波器的性能指标。理论上,数字滤波器的系数应当采用无限精度来表示,但实际中用硬件来实现,将系数量化成有限位数,将引起滤波器频率特性的改变,甚至导致滤波器的不稳定[16]。从量化角度考虑,系数的位数可以选择足够大来保证系统的稳定性,但由于硬件条件的约束,系数位数不可能太大,需要通过仿真确定滤波器系数字长。此处将得到的系数统一量化以满足后续计算要求,且保持系统的稳定性。

本文将不同的系数量化位数和输出量化位数进行比较,从图6、图7可以看出,系数及运算字长均会对滤波器的性能产生影响,综合考虑资源占用率和数据精度,本文选取12 bit系数,16 bit输出量化来满足数字滤波器的滤波效果以及频响稳定性。

图6 IIR滤波器系数有限字长效应

图7 IIR滤波器输出数据有限字长效应

3 IIR数字滤波器软核设计

3.1 IIR滤波器设计原理

根据已知,动态补偿滤波器的离散传递函数为

(5)

b0y(m)+b1y(m-1)+…+bny(m-n)=a0x(m)+
a1x(m-1)+…+anx(m-n)

(6)

因IIR滤波器具有反馈结构,在实现零点系数及极点系数的运算时,应严格满足时序要求,这一结构特点限制了系统的实现速度[17]。为了提高系统的运行速度,零极点系数的运算采用全并行结构,采用移位相加法实现常系数乘法运算。传递函数H(z)可看成由两个FIR型滤波器构成,即式(7)、式(8)中的零点部分(zero parallel)和极点部分(pole parallel)两个部分。

Zero(n)=a0x(m)+a1x(m-1)+…+anx(m-n)

(7)

Pole(n)=b1y(m-1)+…+bny(m-n)

(8)

b0y(m)=Zero(n)-Pole(n)=Ysum

(9)

式(7)、式(8)中:延迟数据y(m-n)和z(m-n)用寄存器保存,与常系数an和bn的乘法运算用左移替代,即将常系数分解成多个2的N次幂数相加的形式,将乘法转换为移位及加法操作。同时用移位运算替代式(9)中除b0操作(此处量化后的b0=1 024,故通过右移10位来实现),得到当前时刻的输出值z(m)。

整个IIR滤波器的闭环求取过程只在求取Zsum的减法器,以及移位运算来实现除法运算的过程中完成。滤波器在求取Zero(n)和Pole(n)、Zsum信号的过程中通过增加寄存器字长来实现全精度运算,出现运算误差的环节只存在于除法运算(即z(m)的求取),此处通过仿真确定输出数据位数精度,减小对输出结果的影响。

3.2 仿真结果分析

将建模所用的实测数据保存成12位的二进制文本作为测试文件的输入信号,用文件IO函数读取,并保存输出数据(数据长度16位的txt文件)。用MATLAB分析理想输出数据和仿真数据曲线,可知拟合效果良好。

仿真图8中,当rst复位信号无效,clk时钟信号为上升沿开始采样,din[11:0](AD采集到的传感器数字信号)给xin[12:0]赋值。xin_reg[5:0]是零点部分Zero(n)输入信号寄存器,将输入信号xin[12:0]依次延迟保存下来。mult_reg[5:0]用来保存aix(m-i)值,xout[30:0]是零点部分计算结果Zero(n)。极点部分pole(n)同理,yin[15:0]保存最终计算结果y(m)。

图8 IIR滤波器仿真图

4 实测结果分析

冲击波测试系统的电路设计框图如图9所示,在激励信号的作用下,传感器将测试信号转换成电压信号,通过调理信号电路进行滤波和放大,将输入信号的电平控制在A/D的测试范围内,在FPGA的控制下,A/D量化后的数据流经过补偿滤波器的处理,其结果保存到存储器SDRAM中,通过USB接口和上位机(Labview平台),读取处理后的有效信号,进行下一步的效应分析。

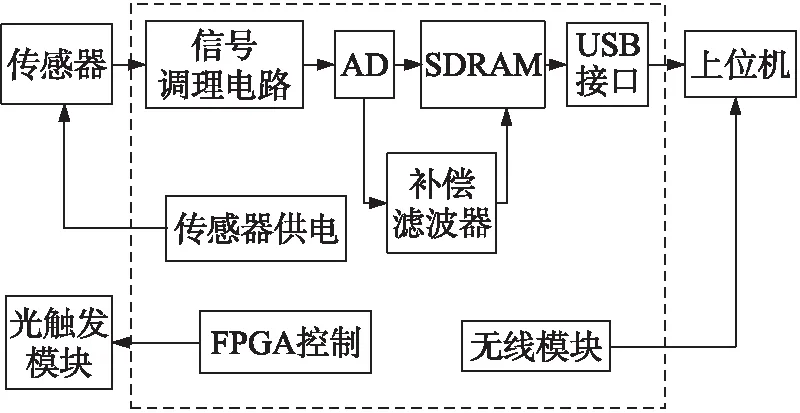
图9 设计框图

用激波管对所设计的滤波器模型进行重复性动态测试,并对输出的二进制文件读取和分析得到对比图,如图10所示,得到补偿前后的动态参数值,如表1所示。可明显看出,该方法补偿效果明显,动态参数改善明显,能为实际冲击波测试提供准确数据。

图10 补偿前后信号对比图

表1 动态补偿前后参数对比

从实验结果可以看出,该补偿系统提高了系统的响应时间,降低了超调量,同时衰减度也近似约等于1,满足系统稳定性的要求,同时提高了系统的有效带宽。从图11中可看出测试系统由补偿前87.1 kHz扩展到172.4 kHz,满足冲击波有效带宽100 kHz(±3 dB)的要求,高频处的噪声影响没有放大,也减小了谐振点对输出信号的影响,动态特性补偿效果明显,满足实际测试冲击波的要求。

图11 补偿前后幅频特性图

5 结论

基于传感器动态补偿原理,利用激波管实验数据,结合QR分解和改进粒子群算法,设计了动态补偿滤波器。根据仿真结果可以看出,该补偿模型很好地修正了由于传感器有效带宽不足引起的动态误差。在考虑数字滤波器的有限字长效应的基础上,选取合适的系数和输出位数,同时补偿滤波器硬件实现采用全并行单反馈结构,避免了设计复杂的反馈电路,保证运算精度的同时提高了运算速度,实现了对传感器动态误差实时修正的目的。实验结果表明,该滤波器补偿效果明显且切实可行。

参考文献:

[1] 何志文. 冲击波超压测试系统动态特性研究[D]. 太原:中北大学,2014.

[2] 刘一江,孟立凡,张志杰,等. 冲击波测试系统中传感器动态补偿装置[J]. 传感技术学报,2012,(11):1516-1521.

[3] 童晓. 爆炸场冲击波压力测量及数据处理方法研究[D]. 南京:南京理工大学,2015.

[4] 赖富文,张志杰,张建宇,等. 基于动态特性补偿的冲击波测试数据处理方法[J]. 爆炸与冲击,2015(6):871-875.

[5] 佘天莉. 测振传感器的动态特性补偿研究[D]. 中国地震局工程力学研究所,2006.

[6] 李悦,钟新跃. 一种传感器动态误差实时修正方法及其FPGA实现[J]. 核电子学与探测技术,2012(9):1112-1116.

[7] 吴健,张志杰,王文廉. 传感器动态误差高速并行修正方法及其FPGA实现[J]. 传感技术学报,2012,25(1):67-71.

[8] Rivera-Mejía J,Villafuerte-Arroyo J E,Vega-Pineda J,et al. Comparison of Compensation Algorithms for Smart Sensors with Approach to Real-Time or Dynamic Applications[J]. IEEE Sensors Journal,2015,15(12):7071-7080.

[9] 张海龙,刘一江,马铁华,等. 基于DSP和IIR的传感器动态特性改善单元[J]. 传感技术学报,2013,26(9):1254-1257.

[10] 轩春青,轩志伟,陈保立. 基于最小二乘与粒子群算法的压力传感器动态补偿方法[J]. 传感技术学报,2014,27(10):1363-1367.

[11] 黄俊钦. 测试系统动力学[M]. 北京:国防工业出版社,2013:12.

[12] 陈达荣. 基于粒子群优化算法的自适应滤波器电路设计[D]. 西安:.西安电子科技大学,2013.

[13] 刘杨,田学锋,詹志辉. 粒子群优化算法惯量权重控制方法的研究[J]. 南京大学学报(自然科学版),2011,47(4):364-371.

[14] 罗海. 基于FPGA的高速IIR数字滤波器设计与实现[D]. 电子科技大学,2007.

[15] 曾菊容. 基于FPGA的IIR数字滤波器的设计与实现[D]. 西南交通大学,2008.

[16] Wisniewski M,Wcislik M. Digital Equalizer for Data Acquisition Path,Constructed Using IIR Filters[J]. IFAC-Papers on Line,2016,49(25):342-345.

[17] 杜勇.数字滤波器的MATLAB与FPGA实现[M]. 北京:电子工业出版社,2014:8.