微型曲面发光二极管阵列照度一致性研究∗
2018-05-03班章梁静秋吕金光梁中翥冯思悦
班章梁静秋吕金光梁中翥冯思悦
1)(中国科学院长春光学精密机械与物理研究所,应用光学国家重点实验室,长春 130033)
2)(中国科学院大学,北京 100049)
1 引 言
发光二极管(LED)的优势主要表现在发光亮度高、响应速率快、工作寿命长及节能环保等方面[1−5].目前,LED的应用非常广泛,如健康照明、户外显示、医疗通信[6,7]等.研究表明,相比大尺寸LED芯片,微型LED能够承载饱和电流密度更大,调制带宽更高[8,9].2014年,美国苹果公司收购了微型显示屏公司Luxvue,引起了科学机构对微显示器件的广泛关注.微型LED阵列现已被研究用于微显示器件、微投影仪及室内可见光通信等新型热门领域[10−13].曲面微型LED阵列除具有平面阵列基本特性外,还可以实现更广的观测视角、提供更便于摆放携带的使用体验,如制作弯曲手机屏、曲面智能手表屏、广角通信照明光源[14−16]等.LED显示器件作为一阶光源时,可避免由覆盖二阶光学设计引起的能量损失,并减少炫光产生[17,18].将微型LED应用于可见光通信,除可以实现光通信技术绿色低碳、避免信号被截获泄露的优点外,还可以进一步提高通信调制带宽[9].同时,微型LED还可应用于健康照明、植物照明等领域,用于改善人们工作、生活的环境和质量,促进心理、生理健康[6,7].
照度均匀性是评价显示和通信照明器件优良程度的重要参数指标之一,提高照度均匀性可减轻因连续长时间紧张的视觉作业对视觉器官造成的不良影响,同时增强能量利用率[19−21].但目前未见关于提高微型曲面LED照度均匀性的研究报道.
为提高微型曲面LED阵列在显示照明使用方面的性能,本文针对微型曲面LED阵列照度分布均匀性的问题进行研究.采用TracePro光线追迹法计算了柱面显示阵列及球面照明阵列的照度分布.实验对比了微型LED像素单元夹角θ分别为13◦,15◦和17◦时的照度分布,并与相同条件下的理论计算结果进行对比.
2 LED出光模型
LED在空间任意点处照度E(r,θ)分布应满足函数关系[18]:
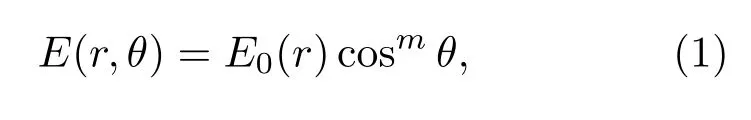
其中,E0(r)表示出光面法线方向上距LED出光面中心r处的照度值,单位为W/m2;θ表示LED任意角度出射光线方向与出光面法线之间的夹角;m为光强分布参数,当m=1时,LED芯片为理想朗伯体;当m>1时,LED为非理想朗伯体.m可具体定义为

其中,θ1/2表示光强下降为法线方向一半时对应的光出射角度.
人眼感知均匀光照性取决于多方面因素,主要为观测者与观测目标的距离、照射光线的入射角度、背景亮度、目标反射率及目标自身的颜色和形状等.为简化计算模型,本文对光照系统做出如下假设:
1)LED阵列的前平面为出光平面;
2)LED阵列表面不添加光学元件及其他封装结构;
3)LED像素单元发光面积小于300µm×300µm,近似为成点光源,可采用照度余弦定理计算远场照度变化;
4)光源到接收平面的距离范围近似等于人眼观察手机屏幕距离的范围;
5)任意LED阵列像素单元具有相等的波长分布和相同的空间辐射通量.
3 柱面显示阵列照度分析
为提高器件在弯曲情况下的照度均匀性,本文以柱面阵列器件为计算模型,分析研究影响微型LED显示器件照度均匀性的主要物理因素.本节分别对两种排布阵列照度分布进行分析计算.将柱面阵列划分为环线阵列及直线阵列两种排布类型,如图1(a)所示.

图1 (a)柱面LED阵列分布示意图;(b)柱面环上两LED辐射照度分布Fig.1.(a)Diagram of the cylindrical LED array distribution;(b)irradiance distribution of two LEDs on a cylindrical curve surface.
3.1 直线阵列照度分布
根据平面照度公式可计算求得轴线方向上LED的照度表达式[18]:

其中,ALED表示发光面积,单位为m2;LLED表示LED法线方向上辐射亮度,单位为W…m2…Sr−1;(x,y,z)表示空间任意点坐标,(x0,y0,0)表示光源点坐标位置.
对轴线上多颗LED像素进行叠加,求得LED阵列轴线方向总照度表达式:

其中,N表示LED数量,n表示正整数,n={1,2,3,………}.
根据(4)式求解得相邻两像素最佳间距d的解析式为

由(5)式可知,直线阵列相邻像素最佳间距d由LED光强分布参数m和像素到接收屏距离z两参数共同决定.
3.2 环线阵列照度分布
柱面环线阵列上LED点光源位置坐标可通过柱坐标(x0=Rsinθ,y0,z0=Rcosθ)来表示,对应到接收平面上任意一点(x,y,z)的LED照度分布表达式,

首先,对柱面圆环上两LED光源照度分布进行计算,如图1(b)所示.θ表示LED光源与光轴夹角,R表示柱面圆环弯曲半径,z表示柱面圆环到探测器的投影距离.
本文将LED辐射照度分布近似成为高斯分布,根据斯派洛法则[2],

其中,σL表示两高斯函数最大平坦距离.此时,将σL最大平坦距离替换为两LED光源法线夹角2θ.两LED组合照度分布函数可表示为
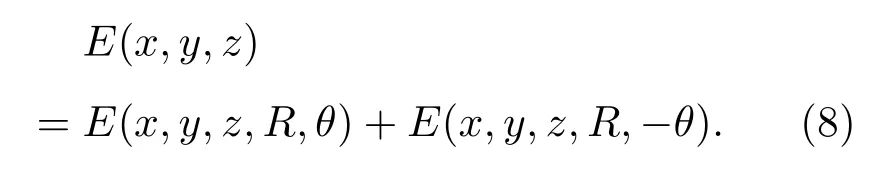
将(8)式进行二阶求导,即∂2E/∂x2=0时,探测器上照度达到最大平坦化.(8)式简化为:
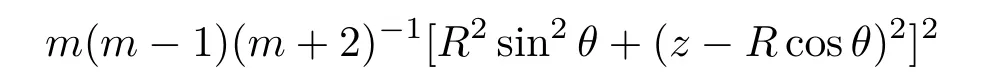

由(9)式可知,环线两LED光源最佳照度值由θ,z,R共同决定.当z≫R时,两LED远场最佳照度分布对应的夹角θ解析式为
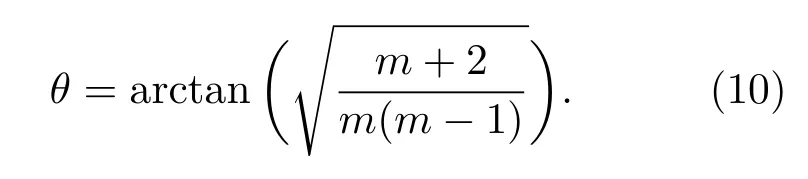
以m=60,z=300 cm,R=5 cm为例进行计算,根据(10)式计算得出光源与光轴夹角θ=7.5◦.将θ参数代入光线追迹系统,获得柱面圆环上两LED组合的照度分布,如图2(a)所示.探测屏中心区域照度达到最大且分布均匀,在{(x,y)|−50 图2 (a)柱面两LED照度分布图,R=5 cm,θ=7.5◦,m=60,z=300 cm;(b)在y=0处x方向的归一化照度Fig.2.(a)Irradiation distribution of two LED source,R=5 cm,θ=7.5◦,m=60,z=300 cm;(b)aty=0,the normalized irradiation distribution alongxaxis direction. 当环线LED像素总数为n时,环形阵列照度分布可表示为 其中,θn表示LED在环线不同位置上对应的角度参数. 将(11)式进行二阶求导,计算得环线LED阵列角度分布与计算参数关系表达式为 根据环线阵列上LED奇偶数量的不同,求解得到的θ函数解析式对应两种情况, 其中,θ0表示环中线与环上相邻LED的圆心线所成张角. 以环线阵列LED数量等于10为例进行计算,设θ0=75◦,R=5 cm,z=300 cm,m=6,根据(13)式求解环线阵列夹角参数θn,代入光线追迹系统获得阵列照度分布,如图3(a)所示.LED阵列照度在x轴方向[−100,100]区间内达到均匀分布,在{(x,y)|−40 在微型显示等应用领域中,提高显示器件照度均匀性可增强使用的舒适度.因此,为进一步提高照度一致性及能量利用效率,对曲面阵列照度进行优化.图4(a)所示为弯曲半径R=5 cm柱面10×10阵列,对其最佳照度分布进行计算.取m=200,θ0=75◦,z=300 cm,根据(5)和(13)式求得阵列像素位置分布参数,将计算参数代入光线追迹系统,获取柱面阵列照度分布.在{(x,y)|−200 图3 (a)1×10阵列照度分布,R=5 cm,θ0=75◦,m=6,z=300 cm;(b)在y=0处x方向的归一化照度Fig.3.(a)Irradiation distribution of 1×10 LED array source,the parameter isR=5 cm,θ=7.5◦,m=60,z=300 cm;(b)aty=0,the normalized irradiation distribution alongxaxis direction. 图4 (a)柱面阵列示意图;(b)10×10阵列照度分布,R=5 cm,θ0=75◦,m=200,z=300 cmFig.4.(a)Diagram of the cylindrical LED array distribution;(b)irradiation distribution of 10×10 LED array source,the parameter isR=5 cm,θ=7.5◦,m=60,z=300 cm. 研究表明,随像素单元尺寸减小,LED电光转换效率逐渐增高[20].为提高通信照明领域光源器件的能量利用效率,可将微型LED阵列替代传统大尺寸LED.同时,可将曲面LED阵列器件作为一阶光源直接用于照明,避免由二阶光源元件引起的能量损失.本文以球面基底为计算模型,分析研究影响环形LED阵列照度均匀性的主要参数. 根据(1)和(2)式求解球面LED单元像素照度分布表达式为: 其中,φ,ξ表示在球面坐标系内LED与x轴和y轴分别所成夹角,R为球面半径. 将球面环线LED阵列照度叠加,求得LED阵列总照度分布表达式为 其中,M表示环数,Ni表示每环上LED数量,n为大于等于3的正整数. 图5 球面环形阵列(a)俯视和(b)侧视图Fig.5. Schematic diagram of spherical ring array:(a)Top;(b)side view. 首先对单环LED阵列照度进行计算.如图5(b)所示,φ表示LED法线方向与环法线方向所成夹角.均匀照度下φ解析式为 由(16)式可知,球面环线LED阵列达到均匀照度与环线上LED像素数量无关.设R=3.5 cm,φ=15◦,m=30,对比环线阵列LED数量分别为5和9时照度分布,如图6(a)和图6(b)所示.在{(x,y)|−100 对带有中心像素单元的球面环型LED阵列照度进行计算分析.均匀照度下,φ解析式为 由(17)式可知,球面环心阵列角度计算结果与球面环形LED阵列对应的结果不同.中心LED像素单元与环LED发光强度所成比例对整体阵列光源照度分布存在影响,计算得知,当中心像素单元与环LED阵列像素单元光通量之比满足(18)式时,环心LED阵列照度分布达到最大平坦程度. 其中,N为环LED阵列单元数量. 图6 环线光源像素数量为(a)5 LED和(b)9 LED照度分布,R=3.5 cm,φ0=15◦,m=30,z=250 cm;(c)5 LED和9 LED环线光源在y=0时x方向的归一化照度对比;(d)环线阵列LED数量分别为3,5,9,15,20时对应的最大平坦化照度值Fig.6.Irradiation distribution of(a)5 LED and(b)9 LED array source,the parameter isR=5 cm,φ0=7.5◦,m=60,z=300 cm;(c)aty=0,the normalized irradiation distribution alongxaxis direction;(d)maximum flatness irradiation of ring LED array with pixel number 3,5,9,15,20. 对比单元数量为6的球面环形阵列与环心阵列照度分布,如图7所示.设定环线阵列参数与环心阵列参数分别为R=3.5 cm,z=250 cm,φ=15◦,m=30和R=3.5 cm,z=250 cm,φ=21.2◦,m=30,Φ=0.64.在{(x,y)|−80 根据(18)式可知,Φ值对整体阵列光源照度分布存在影响.设R=5 cm,z=250 cm,m=3,φ0=52.3◦,计算Φ分别为1,0.1,0.01时阵列的照度分布.随Φ值减小,阵列照度分布均匀性逐渐提高.在{(x,y)|−200 对多环LED阵列照度分布进行计算分析.计算均匀照度下各环阵列上LED法线方向与环法线方向夹角φi表达式为 其中,φ0为第一环上LED法线方向与环法线方向所成夹角,K为各环排布比例因子.根据前文讨论可推知,各环LED出光通量不同,可产生不同照度的分布模式.总照度函数可表达式为 图7 环线光源像素数量为 (a)6LED和 (b)5+1 LED照度分布,R=3.5 cm,φ=21.2◦,m=30,z=250 cm,Φ=0.64;(c)6 LED和(d)5+1 LED像素分布示意图Fig.7.Irradiation distribution of(a)6 LED and(b)5+1 LED array source,R=5 cm,φ=7.5◦,m=60,z=300 cm,Φ=0.64.Schematic diagram of spherical ring array with pixel number(c)6 and(d)5+1. 图8 环心光源Φ值分别为(a)1,(b)0.1,(c)0.01时的照度云图;(d)环心阵列照度分布图Fig.8.Irradiation distribution of the ring LED source withΦvalue:(a)1,(b)0.1,(c)0.01;(d)schematic diagram of spherical ring array. 图9 6+12双环LED阵列分布 (a)俯视和(b)侧视图,两环与环法线夹角分别为φ0和φ1Fig.9.Schematic diagram of two spherical ring array with pixel number 6+12:(a)Top,(b)side view,angle between luminous normal and ring normal isφ0andφ1,respectively. 根据最大平坦化法则可将(20)式可简化为 其中,Ni为各环阵列LED数量,Φi为各环LED单元与第一环LED单元出光通量之比.由(19)—(21)式可知,不同Φ,φ0,K参数下,多环LED阵列可产生多种均匀照度分布模式.设定第一环LED数量为N1=6,第二环LED数量为N2=12,两环线与法线夹角分别φ0和φ1,如图9所示. 保持φ0与K值相同,对Φ=1,5,20时进行计算.φ0=20◦,K=2,R=10 cm,z=200 cm.由于各环LED发光强度不同,在{(x,y)|−200 图10 当Φ值分别为(a)1,(b)5,(c)20时照度分布图,R=10 cm,φ0=20◦,m=5,z=200 cm,K=2Fig.10.Irradiation distribution of the ring LED source withΦvalue(a)1,(b)5,(c)20;R=10 cm,φ0=20◦,m=5,z=200 cm,K=2. 保持K与Φ值不变,对φ0值分别等于15◦和20◦时进行计算.设Φ=1,K=2,R=10 cm,z=200 cm.在{(x,y)|−200 图11 (a)Φ=1,φ0=15◦,(b)Φ=5,φ0=15◦,(c)Φ=1,φ0=20◦,(d)Φ=5,φ0=20◦的照度分布图Fig.11.Irradiation distribution of the 6+12 ring LED source withΦvalue:(a)Φ=1,φ0=15◦;(b)Φ=5,φ0=15◦;(c)Φ=1,φ0=20◦;(d)Φ=5,φ0=20◦. 图12 (a)Φ=5,K=2;(b)Φ=20,K=0.5;(c)Φ=5,K=0.5;(d)Φ=20,K=0.5的阵列照度分布图Fig.12.Irradiation distribution of the 6+12 ring LED source withΦvalue:(a)Φ=5,K=2;(b)Φ=20,K=0.5;(c)Φ=5,K=0.5;(d)Φ=20,K=0.5. 保持φ0与Φ值不变,对K值分别等于2和0.5时进行计算.设φ0=20◦,Φ=5,R=10 cm,z=200 cm. 在{(x,y)|−200 计算结果表明,球面多环阵列均匀照度分布随K,φ0和Φ等参数的改变产生变化.为在探测区域内获取不同均匀照度模式或最大平坦照度可通过参数枚举法进行计算. 本文采用单元像素尺寸300µm×300µm微型LED阵列.具体制作流程为:1)采用MOCVD生长GaAs基AlGaInP外延片;2)将外延片量子阱结构转移至蓝宝石衬底,并进行像素分割,制备倒装型芯片阵列;3)根据像素阵列尺寸特征制备PDMS模具;4)通过PDMS印章将制备好的Al-GaInP LED像素单元转移至柔性电路基底.将LED阵列置于弯曲半径为1.5 cm圆柱表面进行驱动测试,如图13(c)所示.分别选取相邻两LED像素夹角13◦,15◦和17◦,探测器距离为30 cm,正向开启电压值为1.58 V,利用高清CCD相机进行图像采集,如图13(a)所示.当两像素夹角为15◦时,得到最佳平坦照度,如图13(b)所示,框内为测试结果放大示意图.将光强分布进行归一化处理,采用归一化照度分布的均方根RMS值表征两者照度的均匀性.通过实验测试照度分布得出归一化照度分布均方根RMS值为0.12,理论计算结果归一化照度分布的均方根RMS值为0.10.二者RMS值较小且较为接近,表明照度均匀性较好,且实验与理论计算结果较为一致.曲面阵列照度分布均匀程度因相邻两像素单元夹角不同而产生差异.当相邻两像素夹角大于最大平坦化照度对应的角度时,探测接收面中心出现不均匀分布;随两像素夹角收缩,探测接收面逐渐达到最大平坦化照度;继续收缩夹角,平坦化照度面积缩小,如图13(d)所示. 图13 (a)光照度测试系统;(b)像素夹角15◦时的采集图像;(c)微型曲面LED阵列驱动发光测试;(d)微型双LED照度分布理论计算与实验测试对比Fig.13.(a)Illumination test system;(b)capture images at 15◦angles;(c)drive test of micro-curved LED array;(d)comparison between theoretical and experimental double micro LED irradiance distribution. 本文针对微型曲面LED阵列照度分布一致性的问题进行了研究.采用光线追迹法计算了柱面显示阵列及球面照明阵列的照度分布.结果表明,弯曲半径R和光源辐射参数m是影响柱面阵列照度分布的主要因素,通过计算最大平坦化关系可获得合理的阵列像素排布位置,进而增强器件显示均匀程度,提高能量利用效率.计算球面环形阵列照度分布,结果表明,单环形LED阵列照度均匀性与像素数量无关.影响球面多环LED阵列照度分布的参数主要为环线分布系数K、环法线与第一环阵列光源法线夹角φ0及各环线像素光通量之比Φ.调整球面多环阵列位置参数可产生不同的照度分布模式,为实现微型LED阵列智能照明情景模式的多样化提供理论参考.实验对比了微型LED像素单元夹角θ分别为13◦,15◦和17◦时照度分布,与理论计算结果较为一致. [1]Jiang H X,Lin J Y 2013Opt.Express21 A475 [2]Bao X Z,Liang J Q,Liang Z Z,Qin Y X,Lü J G,Wang W B 2016Chin.J.Lumin.37 1399(in Chinese)[包兴臻,梁静秋,梁中翥,秦余欣,吕金光,王维彪 2016发光学报37 1399] [3]Xue B,Yang H,Yu F,Wang X T,Liu L L,Pei Y R,Lu P Z,Xie H Z,Kong Q F,Li J,Yi X Y,Wang J X,Li J M 2014Optoelectronic Devices and Integration V(Beijing:Spie Press)p9270 [4]Herrnsdorf J,McKendry J J D,Zhang S,Xie E,Ferreira R,Massoubre D,Zuhdi A M,Henderson R K,Ian U,Scott W,Kelly Anthony E,Gu E,Dawson M D 2015IEEE Trans.Electron Dev.62 1918 [5]Ban Z,Liang Z,Liang J,Wang W,Lü J,Qin Y 2017Curr.Opt.Photon.1 143 [6]Chen H W,Wen S S,Ma B X,Fu M,Xie Y 2017Acta Opt.Sin.37 0222001(in Chinese)[陈浩伟,文尚胜,马丙戌,符民,谢雅2017光学学报37 0222001] [7]Chai Y B 2012M.S.Dissertation(Shanghai:Fudan University)(in Chinese)[柴颖斌 2012硕士学位论文 (上海:复旦大学)] [8]Mckendry J J D,Massoubre D,Zhang S,Rae B R,Green R P,Gu E,Henderson R K,Kelly A E,Dawson M D 2011J.Lightwave Technol.30 61 [9]Tian P,Mckendry J J,Gu E,Chen Z,Sun Y,Zhang G,Dawson M D,Liu R 2016Opt.Express24 699 [10]Day J,Li J,Lie D Y C,Bradford C,Lin J Y,Jiang H X 2011Appl.Phys.Lett.99 031116 [11]Liu Z J,Chong W C,Wong K M,Tam K H,Lau K M 2013IEEE Photon.Tech.L.25 2267 [12]Rajbhandari S,Chun H,Faulkner G,Cameron K,Jalajakumari A V N,Henderson R,Tsonev D,Ijaz M,Chen Z,Haas H,Xie E,McKendry J J D,Herrnsdorf J,Gu E,Dawson M D,O’Brien D 2015IEEE J.Sel.Area.Comm.33 1750 [13]O’Brien D,Haas H,Rajbhandari S,Chun H,Faulkner G,Cameron K,Jalajakumari A V N,Henderson R,Tsonev D,Ijaz M,Chen Z,Xie E,McKendry J J D,Herrnsdorf J,Gu E,Dawson M D 2015Broadband Access Communication Technologies IX(Beijing:Spie Press)p9387 [14]Gao D,Wang W,Liang Z,Liang J,Qin Y,Lü J 2016J.Phys.D:Appl.Phys.49 405108 [15]Fang S W 2017Ph.D.Dissertation(Beijing:University of Chinese Academy of Sciences)(in Chinese)[方士伟2017博士学位论文(北京:中国科学院大学)] [16]Liu H J,Lan T,Ni G Q 2014Acta Phys.Sin.63 238503(in Chinese)[刘浩杰,蓝天,倪国强 2014物理学报 63 238503] [17]Shi C Y,Wen S S,Chen Y C 2015Chin.J.Lumin.36 348(in Chinese)[史晨阳,文尚胜,陈颖聪 2015发光学报36 348] [18]Moreno I,Avendaño M,Tzonchev R I 2006Appl.Opt.45 2265 [19]Zhu Z,Ma D,Hu Q,Tang Y,Liang R 2018Opt.Express26 A54 [20]Zhao Z,Zhang H,Zheng H,Liu S 2018Opt.Commun.410 123 [21]Tian P,Mckendry J J D,Gong Z,Guilhabert B,Watson I M,Gu Erdan,Chen Z,Zhang G,Dawson M D 2012Appl.Phys.Lett.101 2217
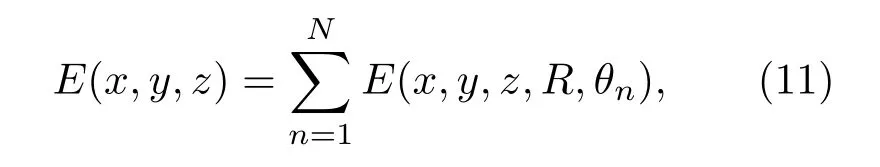

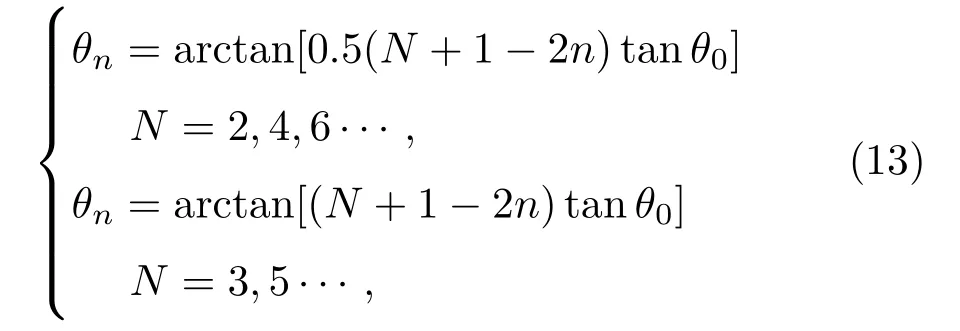
3.3 柱面阵列照度分布


4 球环照明阵列照度分析
4.1 单环阵列
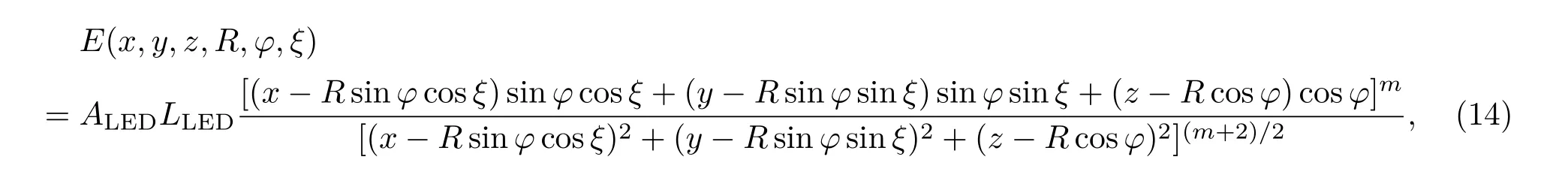
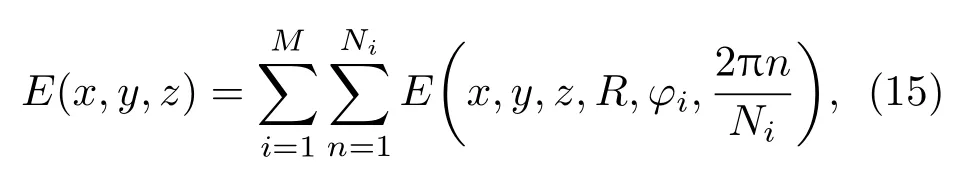

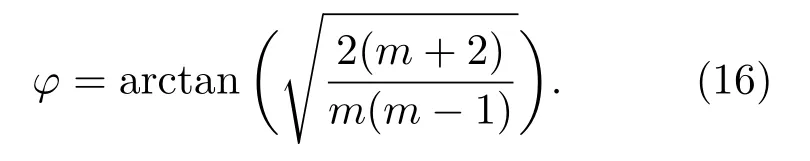
4.2 环心阵列
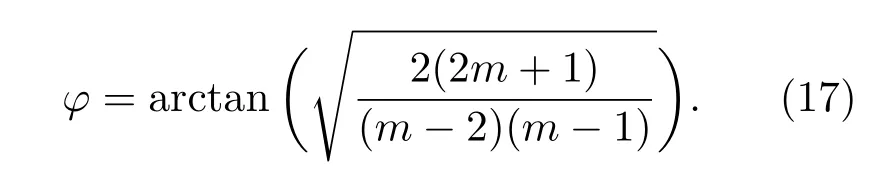


4.3 多环阵列








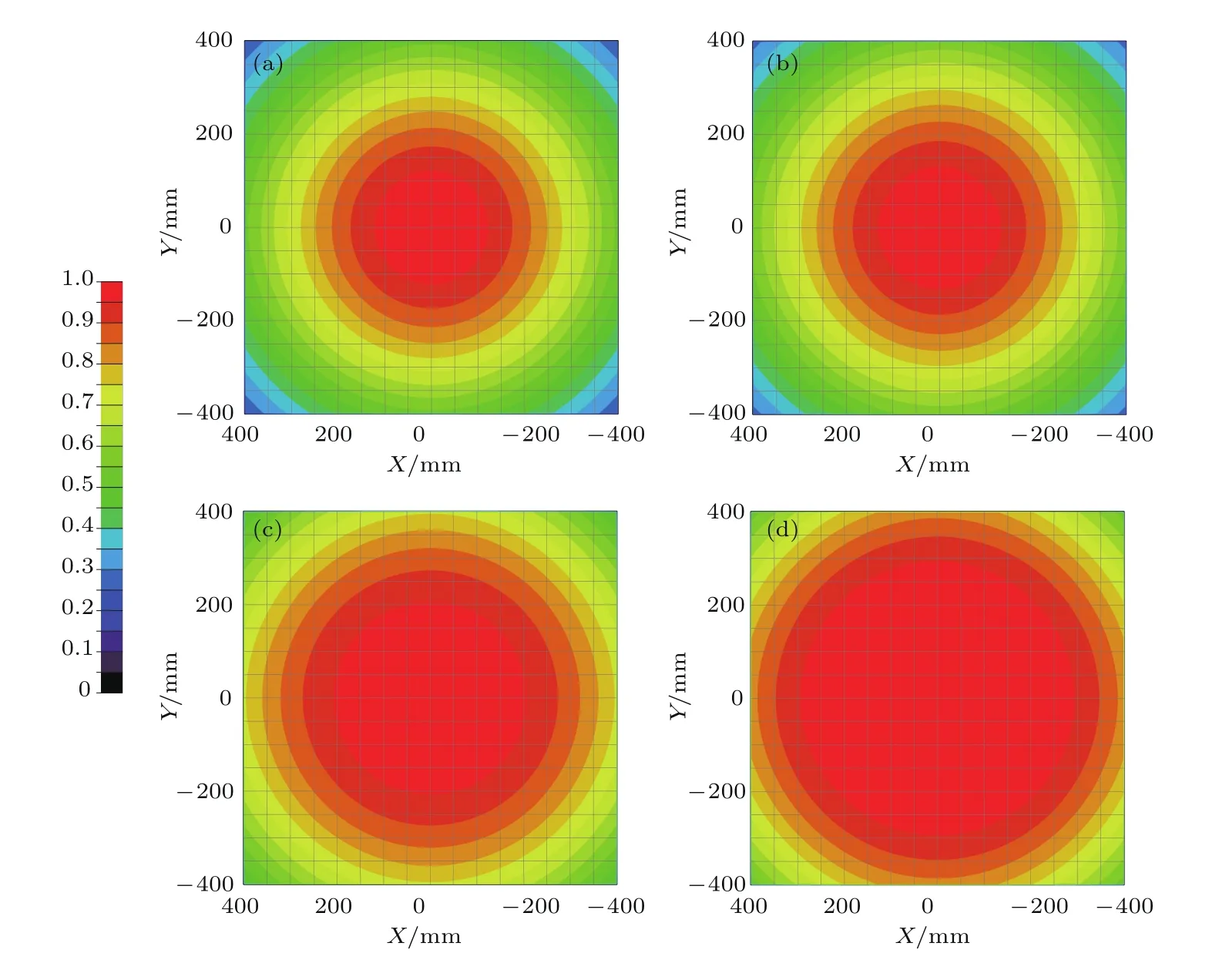
5 实验测试
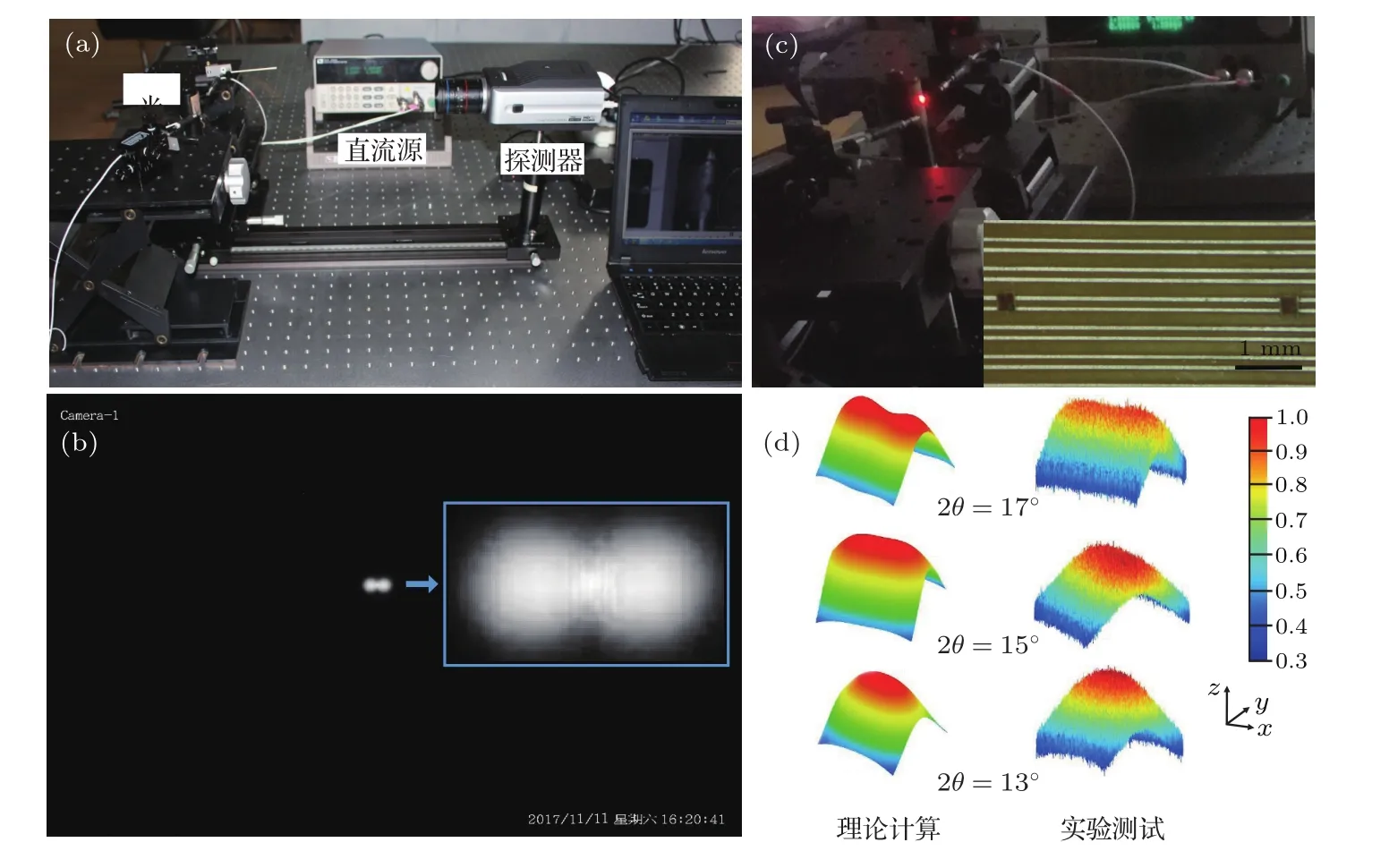
6 结 论
