任意阶标度分形格分抗与非正则格型标度方程

余波何秋燕袁晓

1)(成都师范学院物理与工程技术学院,成都 611130)

2)(四川大学电子信息学院,成都 610064)

1 引 言

理想分抗(元)的阻抗函数

式中µ为运算阶数;s是拉普拉斯变量,亦称运算变量[1,2];F(µ)为分抗特征值,是一个有量纲有单位的物理量[3].分抗元是基本电路元件(电阻、电容、电感、电耦[4,5])的一种很自然的推广,再结合有源元件(比如运算放大器、OTA器件等),便可以实现分数阶微积分运算.

理想的分抗元是不存在的,相对应的近似实现称为分抗逼近电路.构建分抗逼近电路的途径主要有:自然现象与过程的电路建模、µ阶算子s µ的直接有理逼近.常见的经典分形分抗逼近电路,如Oldham分形链类、Sierociuk分形链、Haba分形线分抗等仅具有半阶运算性能且是非理想逼近[1].1960年,Carlson在研究航空线性自适应伺服系统的补偿问题时,提出理想逼近的负半阶对称格型RC网络[6]——Carlson分形格分抗(逼近电路).Carlson分形格分抗通过嵌套能得到−1/2n阶(n为大于或等于2的整数)分抗逼近电路[1,7],但结构复杂,使用的元件数多,无法实现任意分数阶运算(或无法逼近任意分数阶微积分算子).

在对比分析经典的负半阶Oldham分形链与Liu-Kaplan分形链分抗的基础上,文献[8]通过类比拓展构造出三种新型分形链分抗与对应的新型Liu-Kaplan标度方程.标度拓展不仅可以实现任意分数阶分抗,而且能够极大地提高逼近效益,简化电路.标度化的迭代方程——Liu-Kaplan标度方程十分精炼地描述了一大类自仿射自相似分形结构体系所具有的分数幂关系与现象,不仅涉及到分形、电解金属电极界面、粗糙度、标度因子等物理概念,而且具有广泛的物理、化学、生物等现实背景因素,从而受到人们特别的关注[1,8,9].

本文旨在类比拓展Carlson分形格分抗及其归一化迭代方程,获得具有高逼近效益的任意阶标度分形格分抗和可物理实现的格型标度方程(任意分数阶微积分算子有理逼近),并从理论与实验等角度证明标度拓展的有效性.

任意阶标度分形格分抗逼近电路和格型标度方程可广泛的应用于分数阶混沌系统[10,11]、分数阶线性系统[12,13]、分数阶流变模型[14]、分数阶蠕变模型[15]、分数阶忆阻器[7,16]和水轮机调节系统[17−19]等的电路建模与仿真、理论计算或物理实现.

2 Carlson分形格的数学描述与运算性能

2.1 数学描述——迭代电路与迭代方程

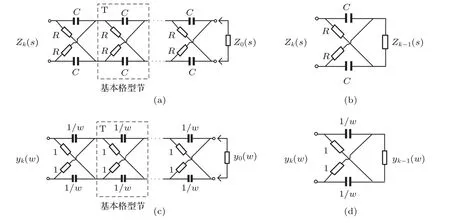
图1 有限k节Carlson分形格分抗逼近电路 (a)原型电路:2k×R,2k×C;(b)(代数)迭代电路;(c)归一化原型电路;(d)归一化迭代电路Fig.1.Finitek-stage Carlson fractal-lattice fractance approximation circuit:(a)Prototype circuit 2k×R,2k×C;(b)algebraic iterating circuit;(c)normalized prototype circuit;(d)normalized iterating circuit.

有限k节Carlson分形格分抗逼近电路[1,6]如图1(a)所示,当给定一个初始阻抗Z0(s)时,输入阻抗函数Zk(s)由迭代公式

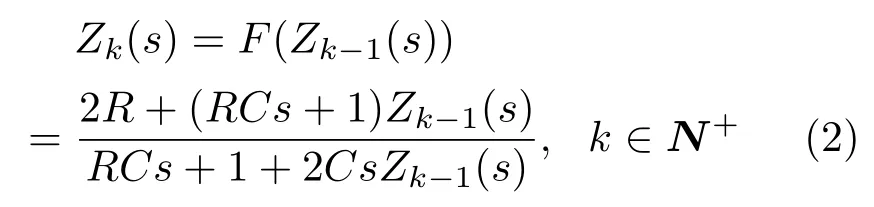
算出,式中k表示电路的基本格型节的节数;R和C分别是电路中电阻的电阻值和电容的电容量.代数迭代式称为Carlson分形格分抗的迭代函数.由(2)式可画出等价的(代数)迭代电路(图1(b)).

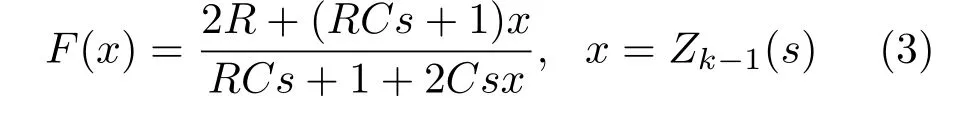
迭代电路与迭代方程

完全表征了Carlson分形格分抗的基本运算性能.

令

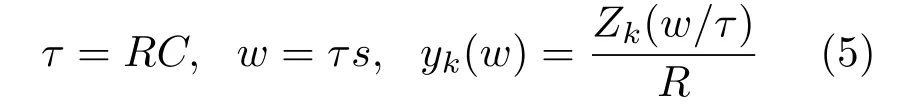
(式中τ是时间常数,w称为归一化运算变量,yk(w)称为归一化阻抗函数).则得到(2)式的归一化迭代形式

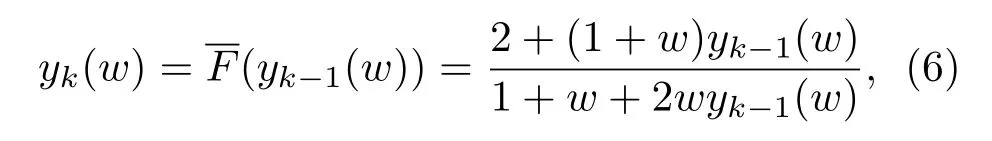
其中

称为Carlson分形格分抗的归一化迭代函数.由(6)式画出归一化迭代电路如图1(d)所示.

归一化迭代方程

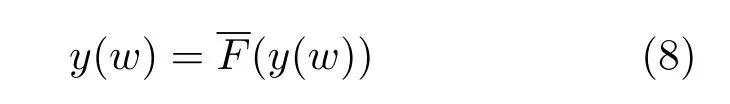
的算术根yC(w)=w −1/2是Carlson分形格分抗的(归一化)极限阻抗,即有

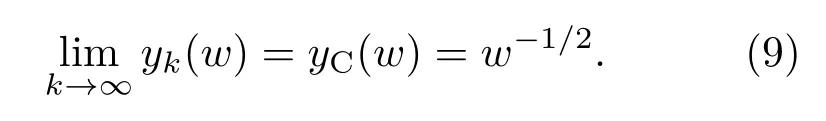
这表明Carlson分形格分抗是负半阶(即µ=−1/2)算子w −1/2的全频有效的理想逼近[1].

2.2 运算性能与逼近性能分析

当y0(w)=∞(即开路)时,k节Carlson分形格分抗的归一化阻抗[1]

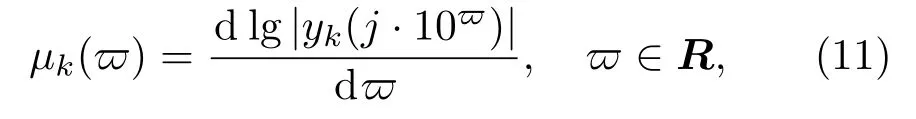
与相频特征

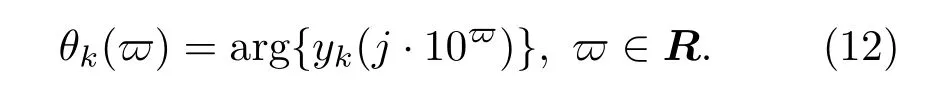
阶频特征µk(ϖ)与相频特征θk(ϖ)曲线(图2(a)与(b))刻画分抗逼近电路的运算性能与逼近性能[1−3,8,9,20−22]. 由运算特征曲线(图2(a)与(b))可得Calrson分形格分抗电路的逼近带宽指数[1]

图2 运算特征曲线 (a),(b)Carlson分形格分抗电路——标度拓展前:α=β=1,σ=αβ=1;(c),(d)正比拓展标度分形格分抗电路:α=β=2;(e),(f)反比拓展标度分形格分抗电路:α=β=1/2Fig.2.Operational characteristics plots:(a),(b)Carlson fractal-lattice fractance approximation circuit before scaling extensionα=β=1,σ=αβ=1;(c),(d)scaling fractal-lattice fractance approximation circuit by direct proportion extensionα=β=2;(e),(f)scaling fractal-lattice fractance approximation circuit by inverse proportion extensionα=β=1/2.

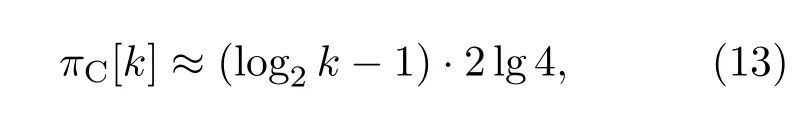
逼近效益——逼近带宽指数与电路节数ςC[k]=k之比:

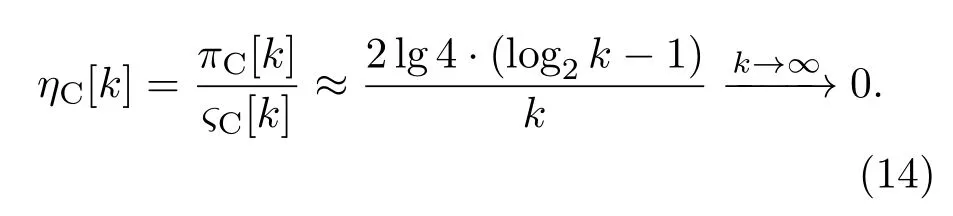
3 标度拓展与标度分形格分抗逼近电路

3.1 标度拓展与格型标度方程

对归一化Carlson分形格分抗(图1(c))进行标度拓展[8],得到图3(a)所示的标度分形格分抗.图3(a)中标示的参量α是电阻递进比、β是电容递进比.α,β统称为分形格分抗电路的标度特征参量,σ=αβ称为该电路的标度因子(scaling factor).当0<α<1,0<β<1时,称为反比拓展;当1<α<∞,1<β<∞时,称为正比拓展.

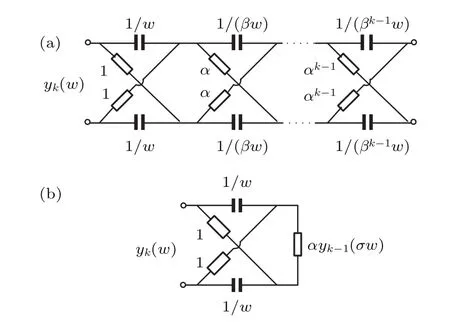
图3 标度分形格分抗及其标度迭代电路 (a)归一化电路:0<α<∞0<β<∞;(b)归一化迭代电路:σ=αβFig.3.Scaling fractal-lattice fractance approximation circuit and corresponding scaling iterating circuit:(a)Normalized prototype circuit 0<α<∞,0<β<∞;(b)normalized scaling iterating circuit:σ=αβ.

有限k节标度分形格分抗逼近电路的输入阻抗函数可由标度迭代公式

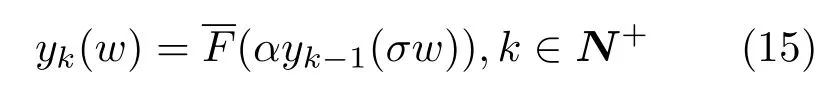
算出.由此画出等价的标度迭代电路如图3(b)所示.

在数学上,标度拓展是将代数迭代方程(8)进行标度变换[8]

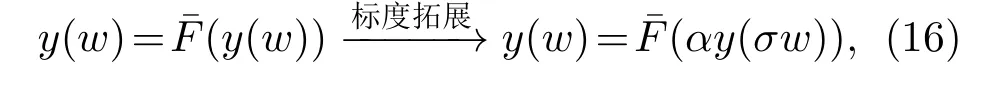
得到一个非正则标度方程——格型标度方程

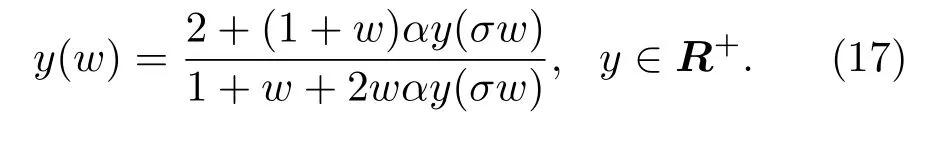
3.2 格型标度方程的近似求解与运算有效性

对于有限k节标度分形格电路(图3(a)),由于每格形节的特征频率

因此正比拓展(1<σ<∞)时,wi向低频扩展.反比拓展(0<σ<1)时,wi向高频扩展.

对于正比拓展获得的有限k节标度分形格电路,考虑y0(w)=∞(即开路)情形.由于

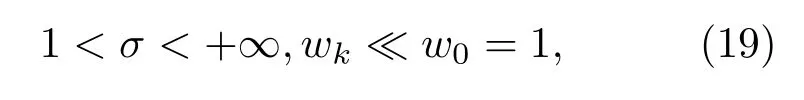
在极高频率条件下(即1<|w|→∞时),电路呈现电阻特性,在极低频率条件下(即1>|w|→0时),电路表现出电容特性,即有

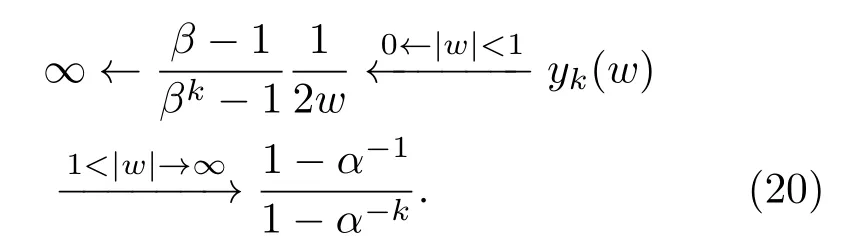
在频段满足

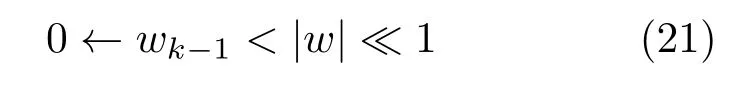
时,电阻与电容共同作用,整个电路呈现出分数阶运算性能.此时,非正则标度方程(17)将简化为正则标度方程

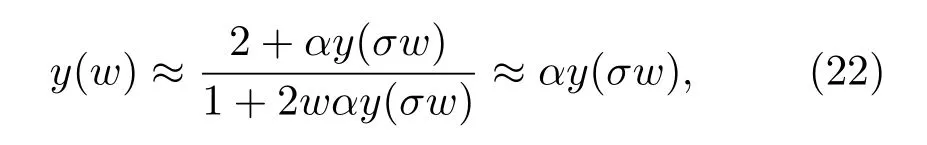
并有近似解

式中,ζ是一个常数,µLiu称为Liu氏运算阶,函数yLiu(w)称为Liu氏粗解.

近似解(23)式表明,通过调节电阻递进比α与电容递进比β的取值,可构造出具有任意Liu氏运算阶的分抗逼近电路.当取α=β=2时,正比拓展得到µLiu=−1/2阶的低频有效分抗逼近电路,其运算特征曲线如图2(c),(d)所示.

反比拓展(0<α<1,0<β<1,0<σ<1)在高频段也可得到同样的Liu氏近似解.当取α=β=1/2时,反比拓展得到µLiu=−1/2阶的高频有效分抗逼近电路,其运算特征曲线如图2(e),(f)所示.

3.3 格型标度方程的真实解与分形格电路的运算振荡现象

近似解(23)式在理论上表明了格型标度方程(17)所描述的电路具有分数阶运算性能.当前在数学上直接精确求解方程(17)是困难的.但根据电路的级联结构特点,使用传输参量矩阵法[1,8,9],或使用标度迭代公式

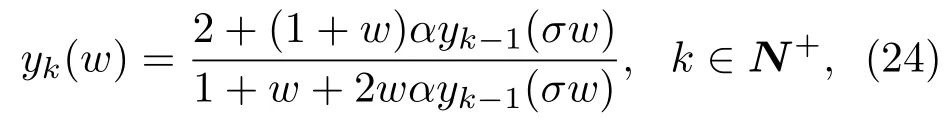
在给定一个初始的有理阻抗函数y0(w)时,比如y0(w)=∞(即初始阻抗开路),可以求出一个有理的输入阻抗函数序列{yk(w)}k∈N,使得

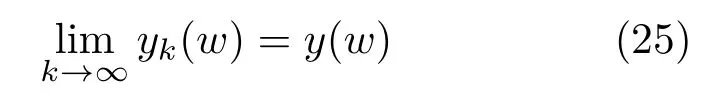
是非正则标度方程(17)的一个真实解——标度分形格电路的极限阻抗函数.

取定标度因子σ ̸=1,由µLiu=−lgα/lgσ得电路的标度特征参量

将这些参量代入(24)式,给定µLiu与σ就能算出相对应的有理阻抗函数序列{yk(w)}k∈N,并由此获得阶频特征µk(ϖ)曲线(图4)与相频特征θk(ϖ)曲线.

由图2与图4可知,标度分形格分抗电路的运算特征产生了运算振荡现象,存在固有的振荡周期

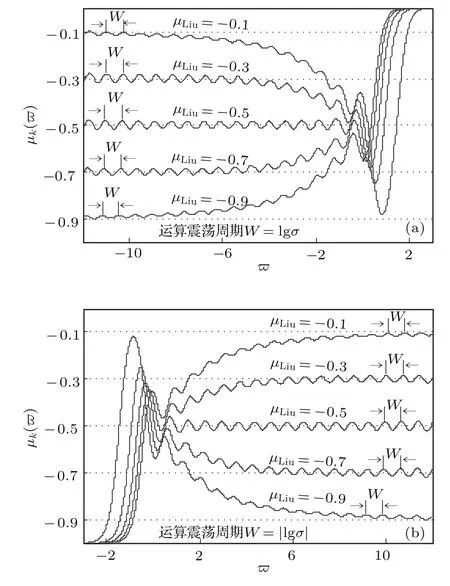
图4 标度分形格分抗逼近电路的阶频特征曲线 (a)正比拓展σ=5;(b)反比拓展σ=1/5Fig.4.Order-frequency characteristic plots of scaling fractal-lattice fractance approximation circuit:(a)Direct proportion extensionσ=5;(b)inverse proportion extensionσ=1/5.

振荡幅度不但与标度因子σ有关,还与运算阶µLiu密切关联.

显然,当σ=1时有W=0,意味着无运算振荡现象.这正好表征了Carlson分形格分抗电路的运算特点(图2(a),(b)).

3.4 标度分形格分抗电路的逼近性能分析

首先考察负半阶分形格分抗电路.此时α=β,σ=αβ,µLiu=−lgα/lgσ.

标度拓展前,α=β=1,逼近带宽指数πC[k]由(13)式给出,逼近效益ηC[k]((14)式)随节数k的增加迅速减小并趋近于零.标度拓展后,由图2(c)—(f)与图4可求出逼近带宽指数

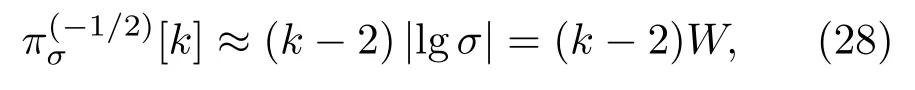
逼近效益

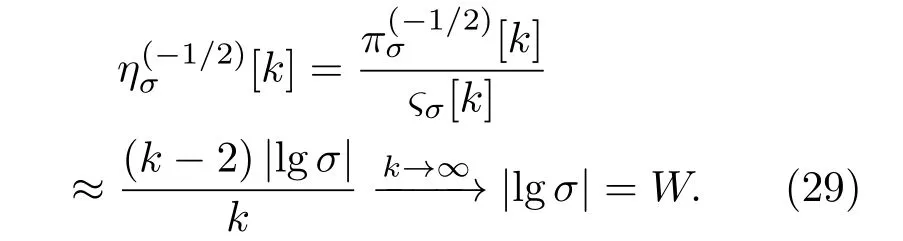
此时可见,标度拓展极大地提高了逼近效益.相对于标度拓展前的Carlson分形格电路,获得的拓展增益

定量表征标度分形格分抗相对于Carlson分形格分抗获得了更高的逼近效益程度.

Carlson分形格分抗的逼近效益ηC[k]与标度分形格分抗的逼近效益η(−1/2)σ[k]曲线如图5所示.由图5可知,通过选择合适的标度因子σ和电路节数k,标度分形格分抗可获得比Carlson分形格分抗更高的逼近效益.由拓展增益函数(30)式得到如图6所示的曲线,当拓展增益gσ[k]>1时,标度分形格分抗的逼近效益高于Carlson分形格分抗.

对于α≠β≠1的情形,µLiu≠−1/2,由阶频特征曲线可求得逼近带宽指数

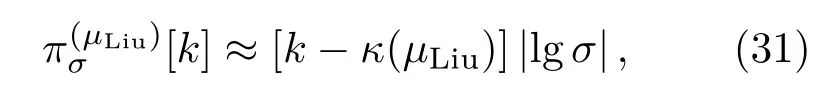
逼近效益

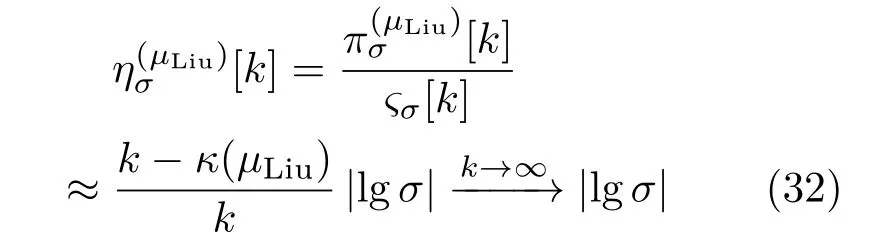
式中κ(µLiu)是由运算阶µLiu确定的正实数.

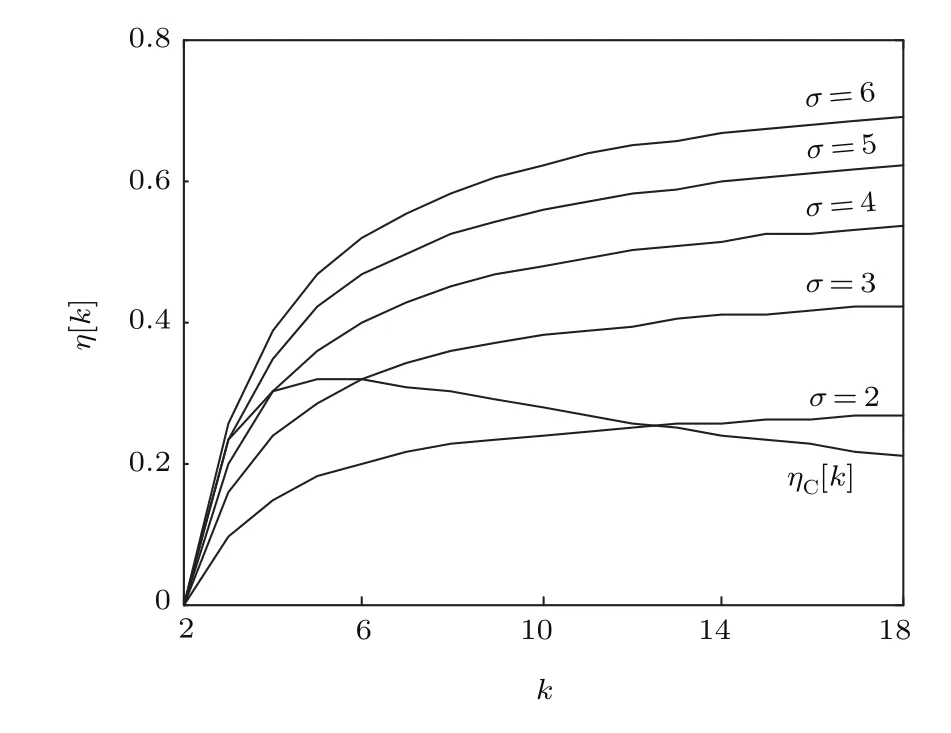
图5 逼近效益对比曲线Fig.5.Contrast curves of approximation efficiency.

图6 拓展增益曲线Fig.6.Extension efficiency curve.

4 实验测试

4.1 测试系统与测试方法

构建有源半阶微分运算电路作为分抗测试电路(图7),取R=300 Ω,C=0.47 µF,分别使用五节Carlson分形格分抗(图1,拓展前α=β=1,σ=1,k=5)与标度分形格分抗(图3,拓展后α=β=2,σ=4,k=5)为分抗元F.

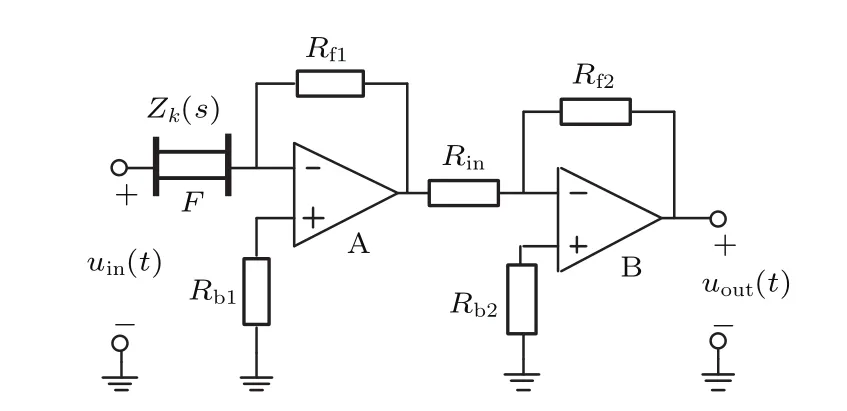
图7 有源半阶微分运算原理电路Fig.7.Active differential operational principle circuit of half order.

图7中运算放大器A,B采用高速电流反馈运算放大器THS3001,Rb1=Rb1=820 Ω,Rin=1 kΩ,Rf1=2.2 kΩ,Rf2=5.6 kΩ. 电阻阻值误差小于5%,电容容量误差小于10%.由电路的电压传输函数(理论上)

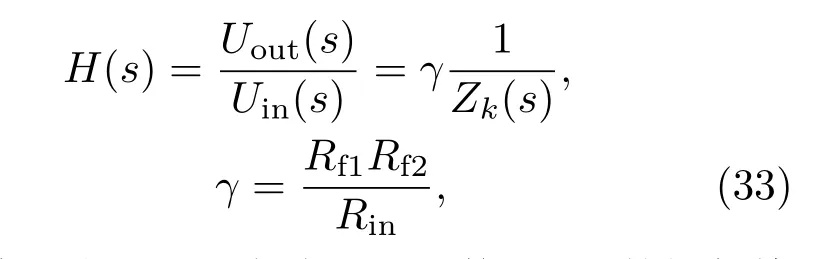
可得到被测分抗逼近电路阻抗函数Zk(s)的幅频特征Ak(ϖ).测量输入正弦电压信号uin(t)的峰-峰值Vinpp(ϖ)、输出正弦电压信号uout(t)的峰-峰值Voutpp(ϖ),则有

进而数值求解分抗的阶频特征

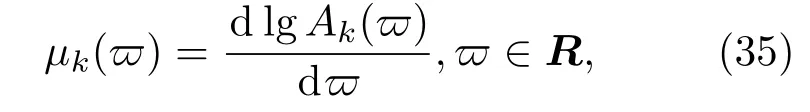
与F特征[22]

正弦信号uin(t)由信号发生器(型号:EE16330)输出,示波器(型号:TDS1012 C)测量信号uin(t)与信号uout(t)的峰-峰值(Vinpp(ϖ)与Voutpp(ϖ)).信号uin(t)是频率在0.1 Hz—1 MHz范围内,ϖ均匀离散变化的正弦信号.实验测试时,控制Vinpp(ϖ)与Voutpp(ϖ)在电路正常工作的电压范围内.

4.2 测试结果与分析

五节Carlson分形格分抗与标度分形格分抗的阶频特征与F特征实验测试结果与理论对比如图8所示.由(35)和(36)式可知,阶频特征和F特征的实验结果需要数值微分运算.由于实验数据固有的误差、数值微分相对于理想微分的误差,造成实验得到的阶频特征和F特征离散较大.使用MATLAB中的smooth函数对数值微分后的数据进行平滑滤波处理,结果如图8所示的星号曲线所示(平滑点为20,lowess平滑方法).

实验测试结果与理论分析相符合,误差主要来源于电路元件参数误差、实验测试仪器误差和平滑滤波误差,且图8(b)所示的阶频特征再次印证了格型标度方程Liu氏近似解的正确性.五节Carlson分形格分抗(拓展前α=β=1,σ=1,k=5)的逼近带宽指数πC[5]≈1.5918,逼近效益ηC[5]≈0.3184,标度分形格分抗(拓展后α=β=2,σ=4,k=5)的逼近带宽指数逼近效益由此可知图8中的运算特征也证明标度分形格分抗相对于Carlson分形格分抗可获得更高的逼近带宽指数和逼近效益,符合图6所示的拓展增益结果.

图8 实验测试结果 (a)Carlson分形格分抗的阶频特征,拓展前σ=1;(b)标度分形格分抗的阶频特征,拓展后σ=4;(c)Carlson分形格分抗的F特征,拓展前σ=1;(d)标度分形格分抗的F特征,拓展后σ=4Fig.8.Experimental test results:(a)Order-frequency characteristic of Carlson fractal-lattice fractance approximation circuit before extension(σ=1);(b)order-frequency characteristic of scaling fractal-lattice fractance approximation circuit after extension(σ=4);(c)F-frequency characteristic of Carlson fractal-lattice fractance approximation circuit before extension(σ=1);(d)F-frequency characteristic of scaling fractal-lattice fractance approximation circuit after extension(σ=4).

5 应用案例——信号的分数阶微分运算

由(35)和(36)式及图8可知,在有效运算频率范围内,五节标度分形格分抗逼近理想分抗的阻抗值

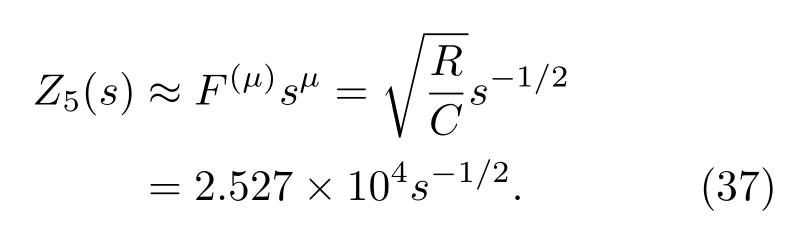
若将五节标度分形格分抗看作理想分抗,则由(33)和(37)式可得图7所示的半阶微分电路的运算关系

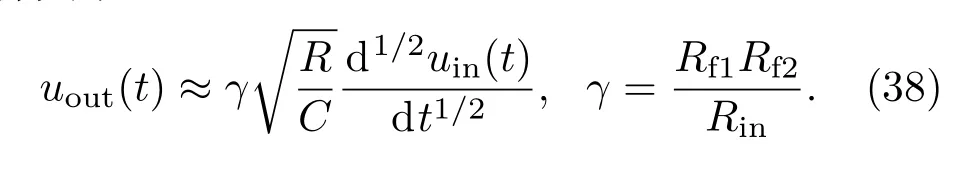
式中,t为时间,uin(t)为输入信号,uout(t)为输出信号.

若输入信号uin(t)为周期三角波,Ω0为基波角频率,T为周期,E为峰峰值,根据周期三角波信号的半阶微分表达式[23−25]

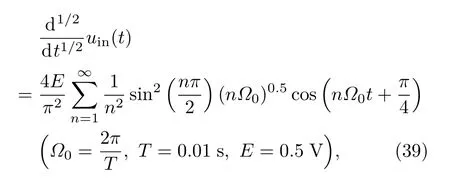
与(38)式,计算半阶微分运算电路的理论输出信号uout(t)(图9(a)),与实验测试结果一致(图9(b)).

若输入信号uin(t)为周期方波,根据周期对称方波信号的半阶微分表达式[23−25]

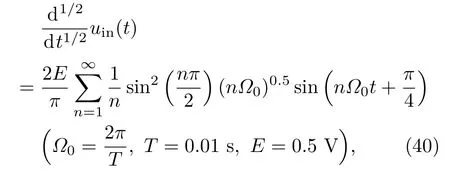
与(38)式,算出半阶微分运算电路的理论输出信号uout(t)(图10(a)),与实验测试结果相符合(图10(b)).

通过输入周期三角波和周期方波,实验测试结果证明图7所示的半阶微分电路能完成信号的分数阶微分运算.

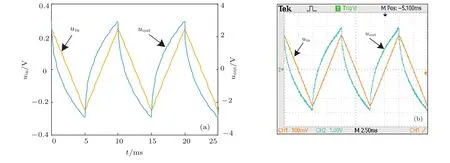
图9 半阶微分电路对周期三角波信号的运算结果 (a)理论分析;(b)实验测试Fig.9.Operational results of differential circuits of half-order for periodic triangular wave signals:(a)Theoretical analyses;(b)experimental measurements.

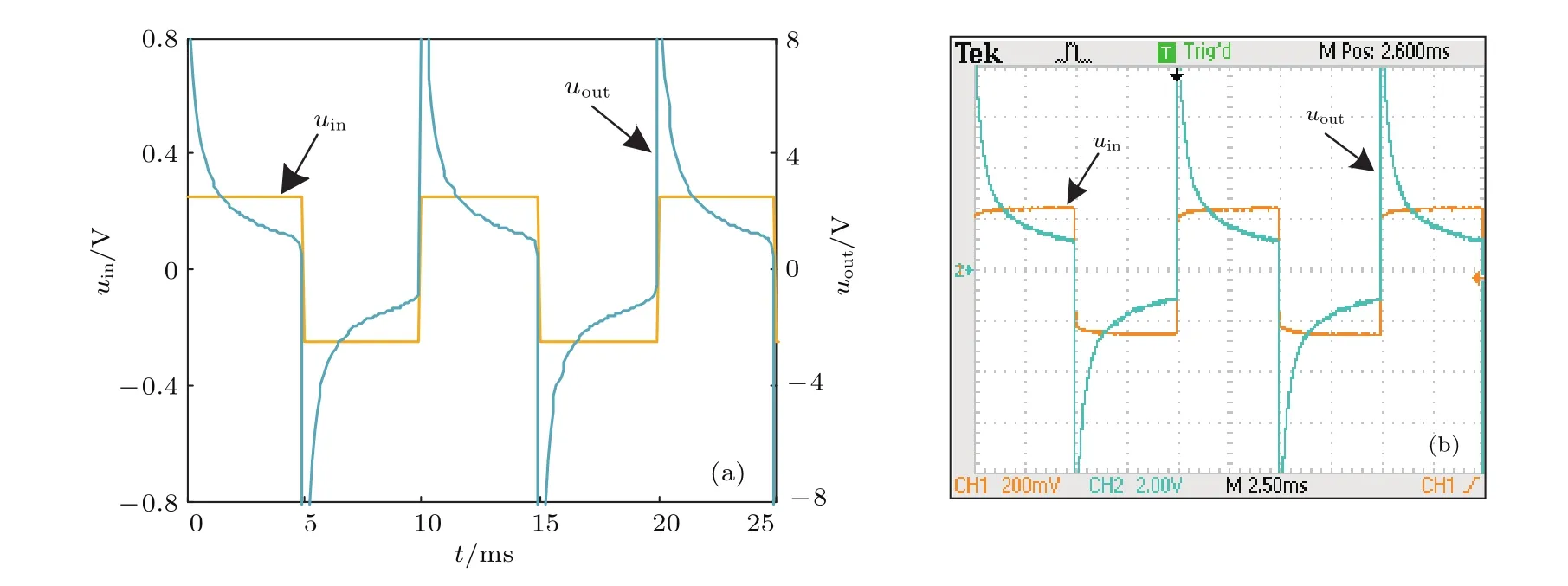
图10 半阶微分电路对周期对称方波信号的运算结果 (a)理论分析;(b)实验测试Fig.10.Operational results of differential circuits of half-order for periodic symmetric square wave signals:(a)Theoretical analyses;(b)experimental measurements.

6 结 论

标度拓展Carlson分形格分抗获得任意阶标度分形格分抗,它完全由格型标度方程(17式)描述.通过调节电阻递进比α、电容递进比β的取值,能够设计任意阶分抗逼近电路.虽然标度分形格分抗的运算特征产生了周期为|lgσ|的振荡现象,但负半阶标度分形格分抗的逼近效益明显高于Carlson分形格分抗.本文同时证明格型标度方程(17)式是一种可物理实现的任意分数阶微积分算子有理逼近.

关于标度分形格分抗与非正则格型标度方程,本文研究仅仅是一个开端,还存在以下亟待解决的问题:

1)标度分形格分抗的运算振荡现象的定性与定量特征研究.

2)获得格型标度方程的真实解的解析表达式是非常困难的.本文初步探讨了怎样求解格型标度方程.若能够得到格型标度方程的真实解的解析表达式,便能描述标度分形格分抗的运算特征的振荡现象,也为求解其他非正则标度方程提供一种思路.

3)运算阶µLiu̸=−1/2的标度分形格分抗,对理想的分数阶微积分算子的逼近效果在归一化特征频率w0附近不甚理想.研究标度分形格分抗的优化也是一件有趣的事,特别是对标度分形格分抗电路的微调整——添加补偿电阻或补偿电容,能显著地提高逼近性能.

[1]Yuan X 2015Mathematical Principles of Fractance Approximation Circuits(Beijing:Science Press)pp3–15(in Chinese)[袁晓 2015分抗逼近电路之数学原理(北京:科学出版社)第3—15页]

[2]He Q Y,Yuan X 2016Acta Phys.Sin65 160202(in Chinese)[何秋燕,袁晓 2016物理学报65 160202]

[3]He Q Y,Yu B,Yuan X 2017Chin.Phys.B26 040202

[4]Shang D S,Chai Y S,Cao Z X,Lu J,Sun Y 2015Chin.Phys.B24 109

[5]Shen J X,Cong J Z,Chai Y S,Shang D S,Shen S P,Zhai K,Tian Y,Sun Y 2016Phys.Rev.Appl.6 021001

[6]Carlson G E 1960M.S.Dissertation(Kansas State:Kansas State University)

[7]Pu Y F,Yuan X 2016IEEE Access4 1

[8]Yuan X,Feng G Y 2015Proceedings of the 26th Academic Annual Conference of Circuits and Systems Branch,Chinese Institute of ElectronicsChang Sha,China,October 23–26,2015 p295[袁晓,冯国英 2015中国电子学会电路与系统分会第二十六届学术年会论文集 中国长沙,2015年10月23日—26日第295页]

[9]Yuan Z,Yuan X 2017Acta Electron.Sin.45 2511(in Chinese)[袁子,袁晓2017电子学报 45 2511]

[10]Han Q,Liu C X,Sun L,Zhu D R 2013Chin.Phys.B22 020502

[11]Wang F Q,Ma X K 2013Chin.Phys.B22 030506

[12]Shen Y J,Yang S P,Xing H J 2012Acta Phys.Sin.61 110505(in Chinese)[申永军,杨绍普,邢海军2012物理学报61 110505]

[13]Yang J H,Zhu H 2013Acta Phys.Sin.62 024501(in Chinese)[杨建华,朱华 2013物理学报 62 024501]

[14]Zhou H W,Wang C P,Duan Z Q,Zhang M,Liu J F 2012Sci.Sin.:Phys.Mech.Astron.42 310(in Chinese)[周宏伟,王春萍,段志强,张淼,刘建锋 2012中国科学:物理学力学天文学42 310]

[15]Wu F,Liu J F,Bian Y,Zhou Z W 2014J.Sichuan Univ.(Engineering Science Edition)46 22(in Chinese)[吴斐,刘建锋,边宇,周志威2014四川大学学报(工程科学版)46 22]

[16]Yu Y J,Wang Z H 2015Acta Phys.Sin.64 238401(in Chinese)[俞亚娟,王在华 2015物理学报 64 238401]

[17]Li H H,Chen D Y,Zhang H,Wang F F,Ba D D 2016Mech.Syst.Signal Process.80 414

[18]Li H H,Chen D Y,Zhang H,Wu C Z,Wang X Y 2017Appl.Energ.185 244

[19]Xu B B,Wang F F,Chen D Y,Zhang H 2016Energ.Convers.Manag.108 478

[20]Tao L,Yuan X,Yi Z,Liu P P 2015Sci.Tech.Eng.15 81(in Chinese)[陶磊,袁晓,易舟,刘盼盼 2015科学技术与工程15 81]

[21]Liu P P,Yuan X,Tao L,Yi Z 2016J.Sichuan Univ.(Nat.Sci.Ed.)53 353(in Chinese)[刘盼盼,袁晓,陶磊,易舟2016四川大学学报(自然科学版)53 353]

[22]Yu B,Yuan X,Tao L 2015J.Electr.Inf.Technol.37 21(in Chinese)[余波,袁晓,陶磊 2015电子与信息学报37 21]

[23]Yuan X,Chen X D,Li Q L,Zhang S P,Jiang Y D,Yu J B 2002Acta Electron.Sin.30 769(in Chinese)[袁晓,陈向东,李齐良,张蜀平,蒋亚东,虞厥邦2002电子学报30 769]

[24]Yuan X,Zhang H Y,Yu J B 2004Acta Electron.Sin.32 1658(in Chinese)[袁晓,张红雨,虞厥邦 2004电子学报32 1658]

[25]Zhao Y Y,Yuan X,Teng X D,Wei Y H 2004J.Sichuan Univ.(Eng.Sci.Ed.)36 94(in Chinese)[赵元英,袁晓,滕旭东,魏永豪2004四川大学学报(工程科学版)36 94]