基于Lorenz模型的集合预报与单一预报的比较研究∗

梁丁顾斌丁瑞强李建平钟权加

1)(南京信息工程大学空间天气研究所,南京 210044)

2)(中国科学院大气物理研究所,大气科学和地球流体力学数值模拟国家重点实验室,北京 100029)

3)(南京信息工程大学物理与光电工程学院,南京 210044)

4)(北京师范大学全球变化与地球系统科学研究院,北京 100875)

1 引 言

大气是一个复杂的非线性系统,任何初始的微小误差都会导致预报结果存在很大的不确定性[1−3].Epstein[4]和Leith[5]提出集合预报解决“单一确定性”预报存在“不确定性”的问题.其基本思想是:针对大气初始状态的不确定性,选取合适的扰动集合,叠加于预报初始分析场上,然后分别向前积分制作预报,得到预报集合.大量研究和业务应用表明,集合预报相对单一预报而言,能有效减小预报误差,改善预报水平,提高预报技巧[6,7].

近年来,集合预报的研究重点主要是:1)初值不确定性;2)模式不确定性;3)集合预报产品释用.在不考虑模式不确定性的理想情况下,集合预报成功的关键在于初始扰动的产生.围绕初始扰动的生成,众多的理论方法被提出,如蒙特卡罗法[5]、时间滞后平均法[8]、增长模繁殖(bred growing mode,BGM)法[9,10]、奇异向量(singular vector,SV)法[11−13]、观测扰动法[14,15]、条件非线性最优扰动法[16,17]、集合卡尔曼滤波(ensemble Kalman fi lter,EnKF)法[18]、集合变换卡尔曼滤波(ensemble transform Kalman fi lter,ETKF)法[19]以及新近发展的非线性局部Lyapunov向量(nonlinear local Lyapunov vector,NLLV)法等[20−22]. 以上述理论方法为基础,国内外学者开展了许多研究工作.例如,Anderson[23]基于Lorenz63理想模型,评估了BGM,SV以及随机扰动等方法的预报表现,指出了随机扰动方法比BGM和SV方法具有更高的预报技巧;封国林等[24]利用Lorenz63模型,对集合预报可能的物理基础进行了探讨;Bowler[25]基于Lorenz96模型的研究结果表明,EnKF方法的预报效果比BGM和SV方法更优.值得注意的是,这些工作主要围绕初始扰动产生方法的比较,虽然取得了许多有意义的结果,但多数研究为大样本平均的结果,较少涉及预报技巧对个例依赖性问题的研究.集合预报的预报表现对具体实验个例的敏感性尚需进一步研究.此外,虽然人们对集合预报初始扰动的生成及其在业务预报中的应用等方面的研究较多[26−31],但对集合平均减小预报误差的物理本质与基础仍需进一步探讨.

本文以Lorenz63和Lorenz96理想模型为例,利用NLLV和BGM方法,选取模型的不同状态为实验个例,研究了集合预报对不同实验个例的预报表现,将结果与单一预报进行对比,并试图从概率分布演化的角度,初步分析集合平均具有较小预报误差可能原因,希望能为集合预报理论和预报技巧的改善提供一定的依据.

2 方法与物理模型

2.1 集合预报初始扰动集合产生

BGM方法是目前生成集合预报初始扰动集合的流行方法之一.该方法被美国国家环境预报中心(National Center for Environmental Prediction,NCEP)长期采用.其借鉴了分析循环中误差增长过程,叠加任意随机扰动,通过模式循环积分使其得到“繁殖”,当该扰动在某种意义上达到饱和时,扰动的大小和分布可被视为实际分析误差快速增长模的估计.BGM方法的具体繁殖循环流程如图1(a)所示:初始时刻,在分析场上叠加一组大小相等、方向随机的扰动,并对受扰状态独立积分.在每个繁殖循环的末尾,将扰动的大小尺度化到初始时刻的扰动大小,并叠加到新的分析场上,进行下一个繁殖循环.如此重复,直至预报时刻,就可以获得一组BGM扰动.

图1 (a)增长模繁殖扰动[10]、(b)非线性局部Lyapunov扰动生成[20]示意图以及(c)集合预报流程图Fig.1.Schematic of(a)bred growing modes[10],(b)nonlinear local Lyapunov[20]perturbations and(c)the flow chart of ensemble forecasting.

理论上BGM方法产生的扰动集合能很好地反映分析误差中的增长成分,但在基本流的演化过程中,任何初始随机扰动都会自然地向相空间中增长最快的主导线性局部Lyapunov向量(linear local Lyapunov vector,LLV)方向偏转[9,10].因此,由BGM方法产生的扰动集合往往存在较高的相似性,从而影响其全局正交性[19,25],导致集合离散度不够.针对上述BGM 方法的局限性,丁瑞强、李建平等[32−35]提出了在非线性理论框架下生成初始扰动的NLLV方法.该方法将非线性局部Lyapunov指数(nonlinear local Lyapunov exponent,NLLE)[20−22]拓展至多维,代表正交的扰动增长(缩小)方向.NLLV方法在保留BGM方法的优点,即对参考和扰动状态直接积分,获取扰动集合的基础上,加入正交化过程,保证扰动严格正交,因而能更好地抓住分析误差的特征.NLLV的繁殖循环流程如图1(b)所示:基本繁殖过程与BGM方法类似,不同的是在每个繁殖循环的末尾,对扰动进行正交操作,得到一组正交的扰动,再叠加到新的分析场上.如此重复,直至预报时刻.需要注意的是,在进行正交操作时,要先确定增长最快的扰动,记为主导非线性局部Lyapunov向量(leading nonlinear local Lyapunov vector,LNLLV),其余NLLV扰动可在LNLLV约束下依次获得.Feng等[20,21]的研究结果表明,NLLV较BGM方法具有更高的预报技巧;与ETKF方法相比,两者预报技巧接近,但NLLV计算所需资源要远小于ETKF.本文采用BGM和NLLV方法生成集合预报初始扰动集合,进行相关预报实验.

2.2 Lorenz模型与实验设计

Lorenz63模型的控制方程如下:

其中,σ=10,γ=28.0,b=8/3,分别为Prandtl数、Rayleigh数以及表示与对流尺度相联系的参数.数值积分采用四阶龙格-库塔方法,积分步长取0.01,记作0.01 tus.在该非线性模型混沌吸引子上,每间隔0.05 tus选取一个状态,作为实验个例的初始态,共计选取N1(N1=104)个真实状态,记为Xt63.

Lorenz96模型作为大气的低阶近似,相较Lorenz63模型更适合于研究大气,已经被广泛应用于大气预测和资料同化的研究中[36].Lorenz96模型对初值异常敏感,且非线性作用强,其动力框架可描述为

其中,Xi为模型变量,F为定常强迫.本文的实验设计中,模型维数等于40,即i=1,2,………,40,强迫项F为8,数值积分采用四阶龙格-库塔格式,积分步长为0.05.对于Lorenz96模型而言,从误差增长程度来看,间隔0.2时间单位大致对应1 d[37].因此本文Lorenz96模型的时间单位统一用天(d)表示.在该非线性模型混沌吸引子上每间隔0.25 d选取N2(N2=N1)个不同状态,记为Xt96,作为Lorenz96模型实验个例的初始态.

为了和实际预报情况接近,我们利用EnKF方法对Xt63,Xt96进行同化,生成对应的分析场Xa63,Xa96.作为比较,将从分析场Xa63,Xa96开始的预报视为单一预报.

Lorenz63模型任意实验个例i(i=1,2,………,N1)的集合预报实验设计如图1(c)所示:在T1时刻的分析场上叠加M(M=2)个初始随机扰动,扰动的模与真实分析误差|Xa63i−Xt63i|一致,分布服从[−1,1]上均匀随机分布;从叠加扰动后的分析场出发,分别进行周期为0.1 tus,总时长为0.4 tus的繁殖循环,到T0时刻,产生M个NLLV和BGM扰动;在T0预报时刻的分析上分别叠加和扣除M个扰动后得到2M个扰动场,将扰动场和分析场分别向前积分5 tus,对所有的预报成员采取等权平均,得到集合平均预报.

Lorenz96模型集合预报实验设计与Lorenz63模型类似:在T1时刻的分析场上叠加M(M=5)个初始随机扰动,扰动的模与真实分析误差|Xa96i − Xt96i |相等,分布服从[−1,1]上均匀随机分布;从叠加扰动后的分析场出发,分别进行周期为1 d,总时长为5 d的繁殖循环,到T0时刻,产生M个NLLV和BGM扰动;在T0预报时刻的分析上分别叠加和扣除M个扰动后得到2M个扰动场,将扰动场和分析场分别向前积分12 d,对所有预报成员采取等权平均,得到集合平均预报.

3 结果与讨论

3.1 集合平均预报的整体表现

首先以均方根误差(root mean square error,RMSE)[38]和型异常相关(pattern anomaly correlation, PAC)[38]为标准,通过与单一预报的比较,评估Lorenz63模型和Lorenz96模型集合平均的整体预报表现.图2给出了所有实验个例的平均RMSE和PAC演化过程.比较发现,对Lorenz63和Loren96模型而言,随着时间推移,NLLV和BGM两种集合平均的预报技巧较单一预报都有明显的改善,而NLLV比BGM表现更优.在预报初期(图2((a),(b))中0.6 tus 前;(图2(c),(d))中5 d前),NLLV和BGM集合平均与单一预报结果接近,随着时间的推移,曲线开始出现分离,意味着集合平均的优势开始显现.在预报初期,误差主要以线性增长为主,使得叠加的正负扰动预报对相互抵消.但随着预报时间的延长,非线性作用增强,误差逐渐进入非线性增长阶段,集合平均的非线性滤波作用减小了预报误差[10,39,40].

图2 Lorenz63模型104个个例的平均RMSE(a)和平均PAC(b),Lorenz96模型104个个例的平均RMSE(c)和平均PAC(d)随时间的变化(黑色实线,单一预报;蓝色实线,BGM集合预报;红色实线,NLLV集合预报)Fig.2.(a)Mean RMSE and(b)mean PAC of 104cases of the Lorenz63 model and(c)mean RMSE and(d)mean PAC of 104cases of the Lorenz96 model as a function of lead time(black solid curve,single forecast;blue solid curve,BGM ensemble forecast;red solid curve,NLLV ensemble forecast).

3.2 个例集合预报表现

3.1节的结果表明,集合平均的预报技巧高于单一预报.但对具体实验个例而言,集合预报是否一定优于单一预报仍不确定.为此,我们从预报误差的角度,分析上述个例的集合预报表现.

Lorenz63模型(图3(a)—(b)),Lorenz96模型(图3(d)—(f))所有实验个例的NLLV集合平均和单一预报误差如图3所示.两模型的结果基本一致,预报初期,集合平均和单一预报的预报误差主要集中在“对角线”附近,意味着多数实验个例,其集合平均和单一预报误差大致相当.随时间的增加,单一预报误差大于集合平均的实验个例数逐渐增多,多数实验个例落入单一预报一侧(BGM的结果与NLLV一致).

进一步集合平均误差小于单一预报误差的实验个例占总实验数的比例(k)如图4所示.在预报开始阶段,k≈50%.随时间推移,k逐渐增大,集合平均的优势愈发显著.Lorenz63模型第5 tus时刻的NLLV和BGM集合平均预报的k值分别为65%和62%.Lorenz96模型第12 d时刻的NLLV和BGM集合平均预报的k值分别为95%和86%.值得注意的是,对所有预报时刻,NLLV集合平均占优的百分比都较高于BGM,这可能是由于NLLV的严格正交,导致其能捕捉更多的误差分量,从而更准确地刻画初始误差向量[20,21].正如图5所示,对于Lorenz63模型而言,当γ>24.74时,系统表现出不同复杂程度的混沌行为,计算表明,NLLV的这一优势不随γ值的变化而变化.

图3 Lorenz63和Lorenz96模型104个个例在第(a)1 tus,(b)3 tus,(c)5 tus和在第(d)1 d,(e)7 d,(f)12 d时刻的NLLV集合平均和单一预报的预报误差Fig.3.Forecast error of NLLV ensemble mean and the single forecast of 104cases of Lorenz63 and Lorenz96 model at time(a)1 tus,(b)3 tus,(c)5 tus and at time(d)1 d,(e)7 d,(f)12 d,respectively.

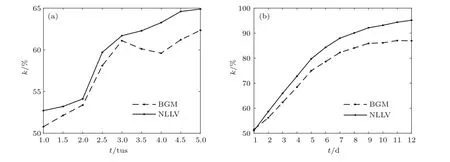
图4 Lorenz63模型(a)和lorenz96模型(b)集合平均预报比单一预报误差小的实验个例百分比随时间的演变(点虚线,BGM集合平均;点实线,NLLV集合平均)Fig.4.Ratio of the cases of the NLLV(dot-dashed line)and BGM(dot-solid line)ensemble mean forecast with smaller error compared with the single forecast as a function of time from(a)Lorenz63 model and(b)Lorenz96 model.

图5 Lorenz63模型NLLV(实线)和BGM(虚线)104个实验个例在预报第5 tus时的k值随γ的变化Fig.5.Ratio of the NLLV(solid line)and BGM(dashed line)ensemble mean forecast with smaller error compared with the single forecast at 5 tus as a function ofγof Lorenz63 model.

3.3 吸引子概率分布特征

吸引子的概率分布反映了系统的长期行为特征.吸引子上不变的概率分布是其基本特征[41].图6给出了Lorenz96模型的变量X(X为任意变量)在不同长度的积分序列下的概率分布.很明显可以看出,随着演化时间趋于无穷,变量X的空间概率分布趋向不变,这意味着系统轨迹会以不变的概率在吸引子上演化.

图7给出了不同预报时刻Lorenz96模型变量X的集合平均预报状态和单一预报状态的概率分布.对单一预报状态而言,其概率分布在各预报时刻都与真实状态的概率分布基本保持一致,这是因为在理想模型条件下,单一预报状态同样位于参考状态的吸引子上,其大样本集合等于参考状态的吸引子集;而集合平均预报,其概率分布随时间呈现出值域变窄、峰值变大的特点,这是由于集合平均的非线性滤波作用,使得集合平均预报状态的取值缩小到吸引子上的较小区域内(即吸引子的一个子集上).意味着随预报时间的推移,单一预报倾向于选择混沌吸引子上的随机状态进行预报,而集合平均预报则倾向于选择吸引子子集上的随机状态进行预报.

图6 Lorenz96模型变量X概率分布,图中标注为积分步长,黑色虚线为变量X的平均值Fig.6.Probability(%)distribution of variableXof Lorenz96 model with different lengths of integration series.The mean state value(black dashed line)ofXis 2.33.

图7 Lorenz96模型104个实验个例对应的变量X的真实状态(黑线)、单一预报状态(蓝线)及NLLV集合平均预报状态(红线)的概率随时间的变化Fig.7.Probability(%)distribution of the true states(black line,left hand scale),single(blue line,left hand scale)and NLLV ensemble mean(red line,right hand scale)of variableXof Lorenz96 model over the total 104cases as a function of time.

4 结 论

本文利用Lorenz63和Lorenz96理想模型,通过选取吸引子上不同状态作为实验个例,研究了不同实验个例的集合预报与单一预报的预报表现,并分析了集合平均具有较小预报误差的可能原因,主要研究结论如下.

1)从平均效果看,NLLV和BGM集合平均预报的均方根误差和型异常相关较单一预报有明显的改善.预报初期,集合平均与单一预报结果接近;随着时间的推移,集合平均对预报的改善效果越显著.

2)不同的实验个例,其集合预报与单一预报的表现不同.预报早期,集合预报与单一预报的预报技巧相当,随着时间的推移,集合预报优于单一预报的实验个例数逐渐增多.在Lorenz63模型中,预报第5 tus时刻,NLLV和BGM集合平均优于单一预报的实验个例数分别为65%和62%左右;在Lorenz96模型中,预报第12 d时刻,NLLV和BGM集合平均优于单一预报的实验个例数分别为95%和86%左右.

3)就概率分布(f)而言,单一预报状态的f和真实状态基本一致,不随时间变化,而集合平均预报状态f随时间呈现出值域变窄、峰值变大的特点,意味着随预报时间的延长,单一预报倾向于选择混沌吸引子上的随机状态进行预报,而集合平均预报倾向于选择吸引子子集上的随机状态进行预报,这可能是集合平均误差小于单一预报的原因,但具体的物理机制仍需进一步探讨.

上述基于Lorenz模型进行的对比研究结果,对实际的预报业务启发包括:集合预报和单一预报的预报技巧会随着事件的变化而变化,对不同事件的预报,应该综合考虑集合预报与单一预报的预报效果;由于集合平均更趋向于系统的平均状态,对于系统中的极端事件,集合预报的预报效果可能会弱于甚至是差于单一预报.

集合预报作为减小预报结果不确定的可行办法,值得进一步利用更加复杂的模型(如Weather Research and Forecasting,WRF模式),以不同天气事件为例,研究其预报表现,为集合预报理论发展和预报技巧的改善提供科学依据.

[1]Lorenz E N 1963J.Atmos.Sci.20 130

[2]Chou J F 1990New Advances of Atmospheric Dynamic(Lanzhou:Lanzhou University Press)p214(in Chinese)[丑纪范1990大气动力学的新进展(兰州:兰州大学出版社)第214页]

[3]Li J P,Chou J 1996Chin.Sci.Bull.41 587

[4]Epstein E S 1969Tellus21 739

[5]Leith C E 1974Mon.Wea.Rev.102 409

[6]Fritsch J M,Hilliker J,Ross J 2000Wea.Forecasting15 571

[7]Visloscky R L,Fritsch J M 1995Bull.Amer.Meteor.Soc.76 1157

[8]Hoffman R N,Kalnay E 1983Tellus35A 100

[9]Toth Z,Kalnay E 1993Bull.Amer.Meteor.Soc.74 2317

[10]Toth Z,Kalnay E 1997Mon.Wea.Rev.125 3297

[11]Molteni F,Palmer T N 1993Q.J.R.Meteorol.Soc.119 269

[12]Molteni F,Buizza R,Palmer T N,Petroliagis T 1996Q.J.R.Meteorol.Soc.122 73

[13]Buizza R 1996Mon.Wea.Rev.125 99

[14]Houtekamer P L,Lefaivre L,Derome J,Ritchie H,Mitchell H L 1996Mon.Wea.Rev.124 1225

[15]Houtekamer P L,Mitchell H L 1998Mon.Wea.Rev.126 796

[16]Mu M,Jiang Z N 2008Chin.Sci.Bull.53 2062

[17]Duan W S,Mu M 2009Sci.China Ser.D:Earth Sci.52 883

[18]Evensen G 2003Ocean Dyn.53 343

[19]Wang X,and Bishop C 2003J.Atmos.Sci.60 1140

[20]Feng J,Ding R Q,Liu D Q,Li J P 2014J.Atmos.Sci.71 3554

[21]Feng J,Ding R Q,Li J P,Liu D Q 2016Adv.Atmos.Sci.33 1036

[22]Ding R Q,Li J P,Li B S 2017Adv.Atmos.Sci.34 1027

[23]Anderson J L 1997Mon.Wea.Rev.125 2969

[24]Feng G L,Dong W J 2003Acta Phys.Sin.52 2347(in Chinese)[封国林,董文杰 2003物理学报 52 2347]

[25]Bowler N E 2006Tellus58A 538

[26]Li Z C,Chen D H 2002J.Appl.Meteor.Sci.13 1(in Chinese)[李泽椿,陈德辉2002应用气象学报13 1]

[27]He W P,Feng G L,Dong W J,Li J P 2006Acta Phys.Sin.55 969(in Chinese)[何文平,封国林,董文杰,李建平2006物理学报55 969]

[28]Ma J H,Zhu Y J,Wang P X,Duan M J 2011Trans.Atmos.Sci.34 370(in Chinese)[麻巨慧,朱跃建,王盘兴,段明铿2011大气科学学报34 370]

[29]Tan N,Chen J,Tian H 2013Meteor.Mon.39 543(in Chinese)[谭宁,陈静,田华2013气象 39 543]

[30]Zheng Z H,Feng G L,Huang J P,Chou J F 2012Acta Phys.Sin.61 199203(in Chinese)[郑志海,封国林,黄建平,丑纪范2012物理学报61 199203]

[31]Zhang H B,Chen J,Zhi X F,Long K J,Wang Y N 2014Trans.Atmos.Sci.37 276(in Chinese)[张涵斌,陈静,智协飞,龙柯吉,王亚男2014大气科学学报37 276]

[32]Ding R Q,Li J P 2009Acta Meteor.Sin.67 241(in Chinese)[丁瑞强,李建平 2009气象学报 67 241]

[33]Ding R Q,Li J P 2009Acta Meteor.Sin.67 343(in Chinese)[丁瑞强,李建平 2009气象学报 67 343]

[34]Ding R Q,Li J P,Ha K J 2008J.Geophys.Res.113 D24112

[35]Li J P,Ding R Q 2011Mon.Wea.Rev.139 3265

[36]Lorenz E N,Emanuel K A 1998J.Atmos.Sci.55 399

[37]Lorenz E N 1995Seminar on PredictabilityShinf i eld Park,Reading,United Kingdom,September 4–8,1995 p1

[38]Buizza R,Houtekamer P L,Toth Z,Pellerin G,Wei M,Zhu Y 2005Mon.Wea.Rev.133 1076

[39]Houtekamer P L,Derome J 1994Mon.Wea.Rev.122 2179

[40]Zhuang Z R,Xue J S,Li X L 2011Acta Meteor.Sin.69 620(in Chinese)[庄照荣,薛纪善,李兴良2011气象学报69 620]

[41]Eckmann J P,Ruelle D 1985Rev.Mod.Phys.57 617