基于ADAMS的重载复合搬运机器人动力学仿真分析
2018-05-03杨前明阮益张君
杨前明,阮益,张君
(山东科技大学机械电子工程学院,山东 青岛 266590)
0 引言
工业机器人是典型的多输入多输出的动力学系统,拥有多个关节自由度,各关节运动之间存在错综复杂的耦合作用[1]。由于机器人结构和运动的复杂性,以及成本较高的特点,采用ADAMS软件研究机器人结构与运动特性是常用的基本分析手段。文献资料研究表明,机器人动力学研究可以解决工业机器人系统的控制问题,实现预期轨迹运动和动态性能,同时为工业机器人的最优化设计提供有力的证据[2]。文献[3]利用 ADAMS 软件中的参数化建模和分析功能,以底座最小力矩为优化目标,对码垛机器人的杆长进行参数化设计,结果表明多次优化设计可以获得底座力矩的最优解。文献[4]结合Pro/E和ADAMS中对四自由度搬运机器人工作过程进行动态仿真,分析了4种机器人的运动特性,为进一步研究搬运机器人的运动学和动力学问题以及关节机器人的本体和控制器设计提供了基础。
纺织车间棉筒更换作业复合机器人[5]采用多组平行四边形结构,具有比例放大和保持平衡特性。利用Solidworks软件建立机器人的三维模型,通过ADAMS软件对机器人虚拟样机进行了仿真分析,评估和检测了机器人结构合理性和动力学特性。
1 复合机器人结构
1.1 复合机器人组成与作业特征
重载搬运复合机器人主要由四轴搬运机器人和AGV小车组成,AGV小车负责工位切换和棉桶背负,搬运机器人负责棉桶搬运和更换,两者协调工作。图1为重载搬运复合机器人三维图。

图1 重载搬运复合机器人三维图Fig.1 The graphic model of the heavy-load handing compound robot

图2 搬运机器人机构简图Fig.2 The mechanism diagram diagram of handing robot
图2所示为搬运机器人机构简图,该机器人是一个四自由度码垛式机器人,大臂、平行连杆、回转支架和三角臂组成平行四边形;小臂、水平保持连杆、三角臂和末端支架组成平行四边形,两组平行四边形构造分散了机器人整体受力,可以保证末端支架始终处于水平姿态。大臂、曲柄连杆、小臂驱动连杆和小臂组成的四连杆机构,主要作用是将关节3驱动动力经小臂驱动连杆传递给小臂,使小臂实现上下俯仰运动;这种以轻质连杆作为驱动臂的方式,不但可以增加了机器人臂部传动系统刚度,而且可以使末端支架达到较高的速度和加速度[6]。
1.2 复合机器人结构特征
前置式驱动系统从设计上加大了臂部的重量,使机器人的重心出现在机器人本体以外,不利于机器人整机平衡,所以小臂的驱动系统采用后置方式,通过将电机和减速机安装在旋转支架上,可以改善系统的动态特性和降低系统的运动惯量[7]。
对于复合机器人实际作业受力分析表明,搬运机器人在额定转速与负载条件下,J2轴和J3轴承受的扭矩相对较大,大臂和后臂工况条件相对恶劣[8]。因此笔者以机器人大臂和小臂关键部件为研究对象,探讨分析机器人关键部件在受力条件相对恶劣条件下的运动特性规律。
2 机器人样机建模
本文采用Solidworks三维软件建立机器人虚拟样机模型后,导入到ADAMS仿真环境中,在软件中对模型添加材料属性、约束、驱动函数和外部作用力,确定需要输出的动力学参数,最后进行动力学仿真与分析[9]。图3为动力学仿真流程图。

图3 仿真流程图Fig.3 The flow chart of simulation
2.1 建立机器人三维模型
建立正确合理的三维模型是机器人动力学分析的前提,模型准确与否将关系到仿真数据的正确性。因此,将仿真模型建立得更精确是动力学分析必不可少的环节。因ADAMS三维建模功能弱且过程麻烦,因此在进行ADAMS仿真前需要在Solidworks软件中建立机器人三维模型。
根据机器人设计几何尺寸对构成所有零件进行建模,再组装为装配体。将模型导入ADAMS中后,会出现许多无相对运动的零件。为了在ADAMS中进行正确有效的仿真,在进行模型导入时尽可能简化模型,减少零件数量,忽略螺钉、螺母、垫圈等小零件[10];最终完成机器人的三维模型的建立与装配。简化后的模型主要由固定底座1、回转支架2、曲柄连杆3、小臂驱动连杆4、平行连杆5、水平保持三角臂6、水平保持连杆7、末端支架8、小臂9、大臂10组成,如图4所示。
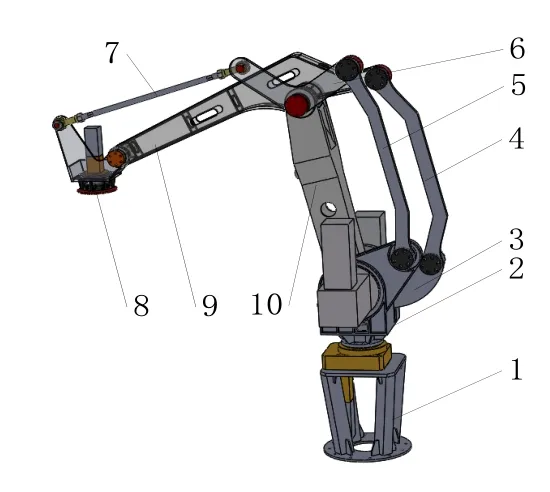
图4 重载搬运机器人三维图Fig.4 The graphic model of the heavy-load handing robot
2.2 添加材料属性和约束
将SolidWorks中的装配体三维图保存为Parasolid格式,并导入到ADAMS中;为了使虚拟样机模型接近于是物理样机模型,需要添加材料、质量等属性;导入到ADAMS中的装配体装配关系将缺失,所以需要重新装配零件。机器人各个构件之间应存在某些约束关系,即一个构件限制另一个构件的运动,这样才能保证各个构件之间有正确的运动。机器人关节应添加运动副,其他零部件无相对运动,添加固定副。机器人主要零件间约束如表1所示。
机器人的建模过程结束,验证模型,观察是否有多余的约束,最终机器人各关节添加约束的仿真模型如图5所示。
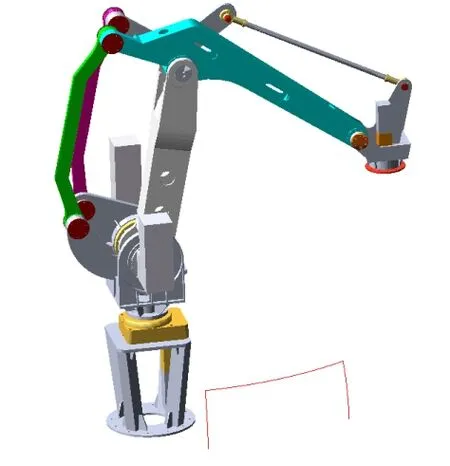
图5 机器人仿真模型Fig.5 The simulation model of robot
2.3 设置运动路径
ADAMS软件对机器人典型工况下进行刚体动力学仿真,不仅能够分析机器人特定关节角位移、角速度、角加速的变化以及路径规划,还可以求解出特定工况下的最大力矩,为电机选型提供理论依据。根据搬运机器人工作流程,可知机器人主要执行棉桶抓取和更换作业任务,运动典型工况轨迹一般为“门”字型,先从原点A0下降到抓取点A1、再A1- A0上升,然后从A0平移到过渡点A2,再下降至摆放点A3,最后A3-A2上升,平移返回至原点A0,其运动路径如图6所示。
2.4 添加驱动函数

图6 机器人的运动路径Fig.6 The motion path of robot
根据路径规划,为这些运动副添加驱动,使两个构件按照确定的规律运动。对机器人四个关节添加旋转驱动,用STEP函数按位移规律进行驱动,各驱动函数如下:
底座关节(J1轴):STEP(time,0,0d,4,0d)+STEP(time,4,0d,6,-30d)+STEP(time,6,-30d,10,-30d)+STEP(time,10,-30d,12,0d)

表1 主要零件的运动约束Table1 Movement restraint between main part
大臂关节(J2轴):STEP(time,0,0d,2,25d)+STEP(time,2,25d,4,0d)+STEP(time,6,0d,8,25d)+STEP(time,8,25d,10,0d)+STEP(time,10,0d,14,0d)
小臂关节(J3轴):STEP(time,0,0d,2,5d)+STEP(time,2,5d,4,0d)+STEP(time,6,0d,8,5d)+STEP(time,8,5d,10,0d)+STEP(time,10,0d,14,0d)
末端执行器( J4轴):STEP( time,0,0d,7,0d)+STEP( time,7,0d ,13,14d)
3 仿真与分析
在驱动函数驱动下,设置仿真控制器的仿真终止时间为14 s,仿真步数为200进行仿真。利用ADAMS/PostProcessor后处理模块对机器人仿真分析,输出关节的角位移、角速度值、角加速度值以及力矩值的曲线如图7、图8所示。
3.1 小臂和大臂角位移、角速度及角加速度曲线
(1)小臂大臂运行特性
分析图7和图8可以看出,大臂和小臂角位移随着时间变化而平缓变化,衔接过渡平滑,无突变;角速度同样随着位移变化加速或减速,各个时间段无间断点;角加速度增大或减小,随时间变化连续,直至最终都为零。这说明机器人各关节在实际作业时,各关节运行稳定且无冲击,满足机械设计要求。

图7 小臂运动规律Fig.7 The law of forearm movement
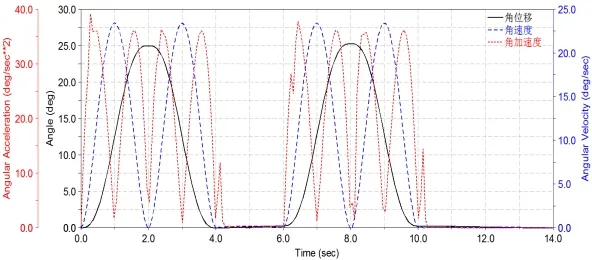
图8 大臂运动规律Fig.8 The law of back arm movement
(2)误差波动及成因
在4~6 s时刻,机器人小臂和大臂角未有动作,仿真曲线应该无位移出现,但在仿真过程中出现位移波动,小臂最大偏差幅值约为0.1,大臂最大偏差幅值约为0.08。误差波动的原因是1轴关节运行出现联动干扰,由于机器人运行是多轴耦合同步控制的过程,各关节间具有耦合作用,表现为某一个关节的运动会对其他关节产生动力效应,使得每一个关节都要承受其他关节运动所产生的扰动,所以实际样机测试过程中不可避免出现误差。
3.2 末端Z轴方向位移
图9是末端Z轴方向位移曲线,末端在开始的4 s内,先下降后上升;在随后的4~6 s内曲线保持水平,在6~10 s内再次经历下降和上升,最后的4 s内在零时刻保持水平稳定。曲线在拐点处过渡稳定平滑,无波动,表明机器人末端运行作业具有良好的控制灵敏度,能按预定的轨迹运行。
3.3 关节力矩
(1)大臂小臂
图10所示为机器人各关节力矩仿真曲线,由图可以看出,机器人各关节力矩变化明显。在初期的0~1.5 s内,大臂和小臂力矩达到峰值;约2 s后关节力矩发生突变。这是由于机器人运行方向发生变化产生冲击。随后又回归正常,开始反向减小直到4 s后消除。
(2)底座
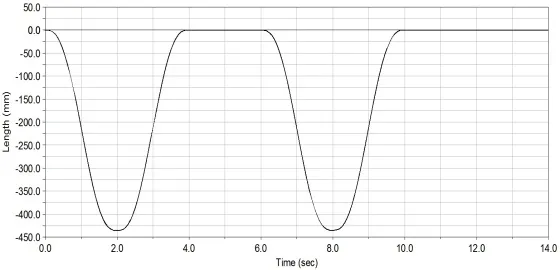
图9 末端Z轴方向位移Fig.9 The end direction displacement of Z-axis

图10 各关节力矩Fig.10 The torque of each joint
在这个过程中,底座力矩没有发生变化;在4~6 s时间内,机器人大臂和小臂力矩保持不变,底座力矩开始发生变化,因为底座转过了一定角度;随后的6~12 s力矩变化类似于前面过程,随着仿真过程的结束,各关节的力矩终变为0 N·m。从系统整个过程来看,运行变化平稳,没有出现剧烈变化现象;所出现的轻微波动是因为受到惯性力及重力的影响。
(3)最大力矩
由图还可以获得大臂最大力矩为272 N·m、小臂最大力矩为198 N·m,底座最大力矩为86.3 N·m,比较机器人所选电机额定扭矩,各关节所达到的峰值均未超过各驱动电机额定力矩,电机选型满足设计要求。
4 结论
根据重载搬运机器人的结构特点,利用SolidWorks软件绘制了机器人的三维模型,采用ADAMS软件模拟机器人典型工况下的作业任务。
(1)关节速度以及加速度曲线随时间均平滑过渡,没有较大的突变,小臂最大偏差幅值约为0.1,大臂最大偏差幅值约为0.08,误差波动来源于各关节间的耦合作用,关节运行出现联动干扰。
(2)机器人末端运行作业具有良好的控制灵敏度,能按预定的轨迹运行;各关节的峰值力矩均未达到电机的额定扭矩,验证了电机选型的正确性。
[1] 王航, 祁行行, 姚建涛, 等. 工业机器人动力学建模与联合仿真[J]. 制造业自动化, 2014(17): 73-76.WANG Hang, QI Hang-hang, YAO Jian-tao, et al. Dynamic analysis and coordinated simulation of industrial robot [J]. Manufacturing Automation, 2014(17): 73-76.
[2] 张良安, 马寅东, 单家正, 等. 4自由度含局部闭链式码垛机器人动力学优化设计[J]. 农业机械学报, 2013, 44(11): 336-341.ZHANG Liang-an, MA Yin-dong, SHAN Jia-zheng, et al. Optimal Dynamic Design of 4-DOF Palletizing Robot with Closed-chain [J].Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(11): 336-341.
[3] 王琪, 曹飞, 张任, 等. 基于ADAMS的码垛机器人参数化分析[J]. 组合机床与自动化加工技术, 2014(7): 45-48.WANG Qi, CAO Fei, ZHANG Ren, et al. Parameterized Analysis of Palletizing Robot based on ADAMS [J]. Modular Machine Tool &Automatic Manufacturing Technique, 2014(7): 45-48.
[4] 张学军, 姜哲珠. 基于Pro/E与ADAMS的搬运机器人动态仿真研究[J]. 机床与液压, 2011, 39(17): 95-97.ZHANG Xue-jun, JIANG Zhe-zhu. Dynamic Simulation of Transfer Robot Based on Pro/E and ADAMS[J]. Machine Tool & Hydraulics, 2011,39(17): 95-97.
[5] 杨前明, 刘亚琼, 王伟, 等. 基于D-H算法的棉桶更换复合机器人运动学建模与仿真分析[J]. 组合机床与自动化加工技术, 2016(12):52-55.YANG Qian-ming, LIU Ya-qiong, WANG Wei, et al. Kinematic Modeling and Simulation Analysis of Cotton Barrel Replacement Composite Robot Based on D-H Algorithm[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(12): 52-55.
[6] 孔民秀, 陈琳, 杜志江, 等. 基于NSGA-Ⅱ算法的平面并联机构动态性能多目标优化[J]. 机器人, 2010, 32(2): 271-277.KONG Min-xiu, CHEN Lin, DU Zhi-jiang, et al. Multi-objective Optimization on Dynamic Performance for a Planar Parallel Mechanism with NSGA-II Algorithm[J]. Robot, 2010, 32(2): 271-277.
[7] 李爱成, 唐火红, 冯宝林, 等. 关节式码垛机器人运动学分析与动力学仿真[J]. 机械设计, 2013, 30(10).LI Ai-cheng, TANG Huo-hong, FENG Bao-lin, et al. Kinematic Analysis and Dynamic Simulation of a Joint Stacker Robot [J]. Mechanical Engineering and Design, 2013, 30(10).
[8] 杨前明, 崔克克, 邵长新, 等. 棉桶搬运复合机器人作业特征分析及其动力电源设计[J]. 新型工业化, 2017, 7(2): 19-25.YANG Qian-ming, CUI Ke-ke, SHAO Chang-xin, et al. The Analysis of Operation Characteristics and Design of Power Supply for Cotton Barrel Handling Compound Robot [J]. The Journal of New Industrialization, 2017, 7(2): 19-25.
[9] 白丽平. 基于ADAMS的机器人动力学仿真分析[J]. 机电工程, 2007, 24(7): 74-77.BAI Li-ping. Simulation Analysis of Robot Dynamics Based on ADAMS [J]. Journal of Mechanical & Electrical Engineering, 2007, 24(7):74-77.
[10] 胡国栋, 许礼进. 基于ADAMS的码垛机器人动力学优化分析[J]. 起重运输机械, 2013(8): 78-81.HU Guo-dong, XU Li-jin. Dynamic Optimization Analysis of Palletizing Robot Based on ADAMS[J]. Hoisting and Conveying Machinery,2013(8): 78-81.
