基于三轴加速度精确测量人体运动能耗的研究
2018-05-03梅婷婷胡钦宇黄淋铃陈凯丽夏海欧梅先明左保齐
梅婷婷,胡钦宇,汤 兴,黄淋铃,陈凯丽,张 磊,夏海欧,梅先明,左保齐
(1.苏州大学纺织与服装工程学院,江苏苏州215006;2.昆山腾飞内衣科技股份有限公司,江苏苏州215320)
1985年,FAO/WHO/UNO三大组织的相关专家委员提出,人体能量需求应以能量消耗的量为标准而不是能量的摄入量。但人体能量消耗是一个多维变量,与运动频率、强度、时间、运动姿态等多种因素相关,因此人体能量消耗是一个随时间不断变化的不稳定数值,且个体的差异导致总能量的消耗量差异较大,这使得能耗测量具有很大的难度。卡路里(简称卡,Calories)是提供人体基本生命活动所需能量的单位,反映及衡量人体健康水平的重要指标之一。精确计算卡路里可以有效的检测人体消耗能量的大小,观察人体表征,预防和减少一些慢性疾病的发生。很多研究人员对能量消耗和卡路里的计算发表了自己的见解,现有的测量能耗的方法主要是测热法、计步器法、心率测量法和加速度传感器法。测热法包括直接测热法和间接测热法。美国卫斯理安大学W.O.Atwato 和E.B.Rosa教授根据直接测热的原理设计了人体量热计。但运用直接测热法对设备和技术的要求较高,费用也较高,因此在不发达地区大规模研究使用不太实际。间接测量法是通过测量人体运动过程中氧气消耗量来估量能量消耗的方法,这种方法技术要求低,费用也较小,但分析仪体积较大不适合户外运动耗能的测量。当前移动健身类的APP大多都采用计步器,结合人体身高、体重、步长、运动时间、步数、卡路里因子等参数来计算人体运动过程中的能量消耗[1]。而人体运动是复杂多样的,仅计步不能区分慢走、慢跑、快跑,以及伴随的出汗等不同强度的运动状态,测量结果误差较大,不能精确反映人体运动消耗。Rodahletal对北欧渔民的实验证明在有氧运动的范围内,心率和耗氧量呈线性相关[2]。因此Apple Watch、小米手环等智能运动监测设备采用心率监控装置,通过测量心率来区分不同运动强度下的运动能耗,但由于个体间差异较大,心率与年龄、身体状态的相关性较大,使得心率法测量仍具有一定的误差。相较而言,三轴加速度传感器能够较为精确地测量人体运动的强度和频率,并且可以持续测量,是较为理想的测量设备。本文即利用三轴加速度的波峰波谷得到步数,再结合人体温度、出汗、运动时间、卡路里因子得到运动卡路里的计算公式,精确计算人体不同运动状态下的运动能耗。
1 硬件测量最佳位置点的确定
1.1 测量位置点的初步筛选
位置监测点对硬件模块测量精确度有着重要影响[3],考虑更多方面因素,我们决定确定选用一个监测点。常用的位置点有手腕、膝关节、大臂、腋下、右前胸、颈下、腰部等,温度变化测量准确的位置点有腋下、右胸以及颈下。在李丹等人[4]的实验中,将传感器放置于外套上口袋,即前胸位置时传感器加速度矢量平均识别准确性高,下楼及行走达到90%以上。从力学角度来看,测量部位放置于肢体部位时加速度测量准确,如手腕、膝关节、大臂等,但由于手的质量较轻,手腕和大臂的加速度也更大,手腕旋转活动复杂,不能代表全身的运动数据[5]。也有实验将加速度传感器应放置于身体的重心,即躯干部位如腰部。陈莉莉[6]实验指出人体重心位置随着人体运动不断变化,运动中重心无法由一个部位确定,故初步选择时排除腰部。综合考虑后本文将右胸和膝关节作为两个待定监测点,分别进行模块数据测量,对比数据,从而选择出一个最佳位置点。
1.2 测量位置点的确定
余杰等人[7]的实验表明性别、年龄、身高、体重都对行为识别的精确度有影响,因此在确定位置点的实验中,我们选择让同一个人在不同部位放置模块进行实验数据测量以避免无关变量的干扰。
测量方法:将硬件模块分别放在右胸和膝关节部位,分别测量慢走、快走、慢跑、快跑、上楼梯、下楼梯六个运动状态下的加速度数据各十组,求各个状态下加速度峰值平均值、方差。将右胸和膝关节在不同运动状态下的数据均值和方差分布整合到点状分布图,如图1所示。
由图1可知,右胸每个状态下测得的数据均值分布更集中,方差更小,规律性明显。而膝关节数据规律性相对较低,因此可认为右胸数据精度更大。选择右胸作为本文测试模块的放置点。
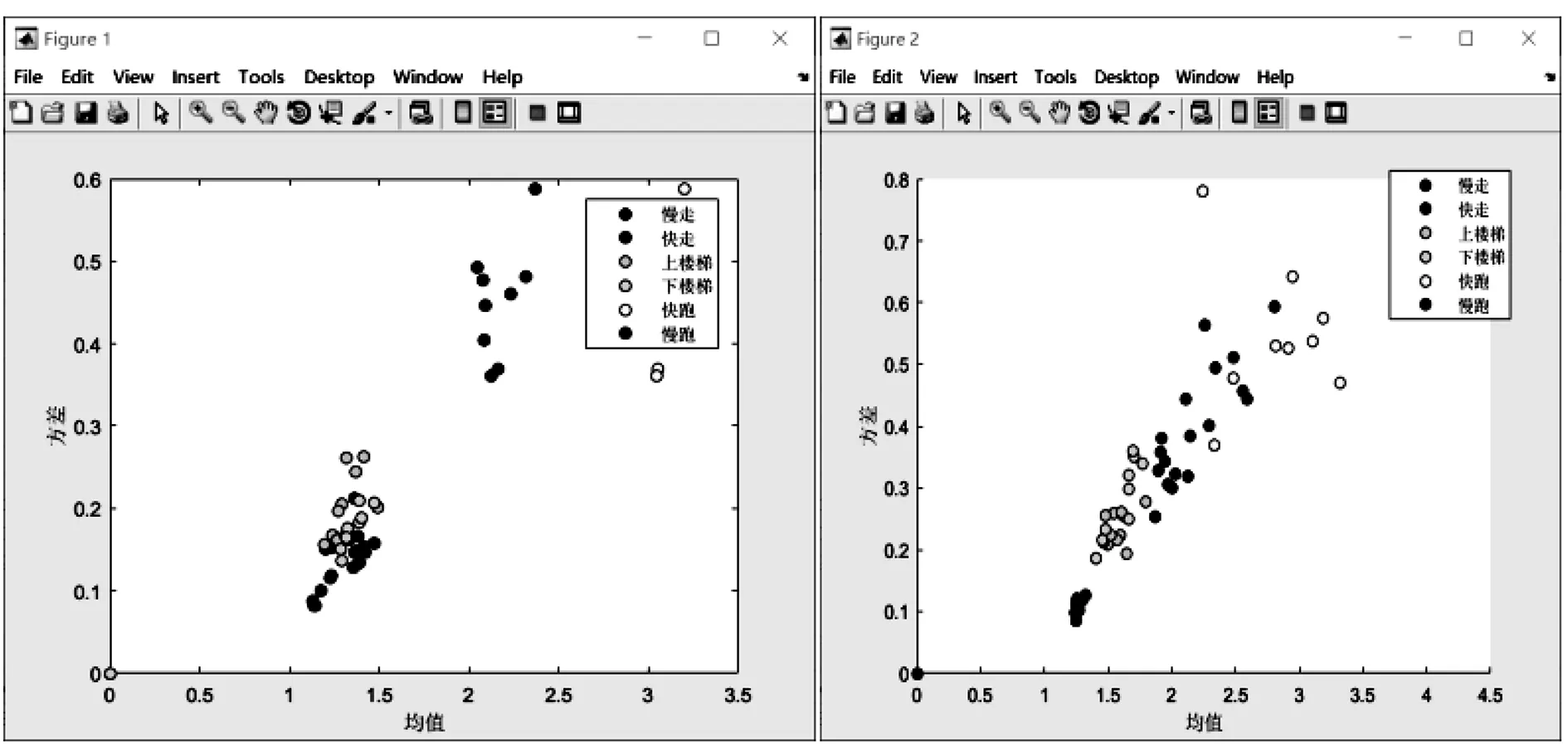
a 以右胸为测量位置点 b 以膝关节为测量位置点 图1 右胸、膝盖加速度均值-方差点分布图
2 人体运动识别
人体运动姿态主要有慢走、快走、慢跑、快跑。由于人体在不同运动强度下消耗的能量不同,欲精确计算不同运动状态下的能量消耗,需要对人体运动状态进行自动识别。本文通过分析各类运动状态下加速度峰值的阈值,得以直观地区分不同的运动状态。测试过程中,人体佩戴硬件模块于右胸位置,在室外进行慢走、快走、慢跑、快跑四类运动,运动2min后开始记录加速度参数变化情况,各类运动分别重复10次,蓝牙模块数据传输频率为6Hz,测得人体前后、左右、上下的加速度分别为a(x),a(y),a(z),计算得到合加速度为:
(1)
式中:a合为合加速度;a(x)为人体前后加速度;a(y)为人体左右加速度;a(z)为人体上下加速度
为了使数据具有更高的准确性,采用滑动平均过滤的方法对合加速度值进行去噪处理.
经过过滤处理的各类运动状态加速度曲线如图2所示。

图2 不同运动状态合加速度-时间曲线
通过观察上面各类各类运动状态合加速度的曲线分布,分析各类曲线的频率、周期、高低峰值等信息,可对各类运动状态进行区分。确定各类运动状态峰值的阈值(w)可以依靠各峰值平均值(χ)和标准方差(σ)来进行,有以下公式[13]:
w=χ±σ/2
(2)
式中w为峰值阈值;χ为峰值平均值;σ为标准方差
通过计算得到各类运动状态加速度峰值的特征阈值已以横线的形式在图中标示出来。横线在图中所示位置表示该类运动状态的平均峰值,可对各类运动进行更为直观的区分。加速度峰值及特征阈值具体数值见表1。

表1 慢走、快走、慢跑、快跑四种运动状态下合加速度峰值均值、方差、阈值
数据处理结果显示,不同运动状态下的加速度阈值存在下列关系:
慢走<快走<慢跑<快跑
利用各个运动状态下合加速度阈值不同可自动识别运动状态。通过输入a(合加速度峰值)落入不同的阈值范围内,得到不同的运动状态,算法流程如图3所示。

图3 人体运动识别流程图
3 不同运动状态下卡路里消耗的计算算法研究
当前移动健身类APP大多通过身高、体重、步数、步长因子、卡路里计算因子这些参数来计算卡路里消耗,只能较为粗略地计算运动能耗。欲精确计算不同运动状态下的运动能耗,本实验采用多元线性回归的方法,利用峰值平均加速度、温度、湿度、运动时间、卡路里计算因子等相关参数推导出各个运动状态下的卡路里计算公式。
(1) 实验对象的选择:为区分不同性别运动能耗的差异,本次实验选取一男一女两位志愿者分别进行实验。女志愿者身高162cm,体重49kg,年龄20周岁,身体健康;男志愿者身高177cm,体重65kg,年龄20周岁,身体健康。
(2) 实验操作:两名志愿者分别佩戴硬件模块于右胸位置,开启硬件模块并与手机移动端通过蓝牙连接成功后,同时开始指定状态的匀速运动,匀速运动2min后开始测试数据。保持匀速的运动状态,5min后结束数据测试,数据导入手机移动端。分别测试慢走、快走、慢跑、快跑四种运动状态的数据各10组。
(3) 实验场地:学校操场室外测量。
数据处理:本实验利用matlab数据处理工具,采用多元线性回归的方法,对能量与运动的关系进行探究,选用了峰值平均加速度、温度、湿度、时间来表述,发现此4个变量与能量消耗的关系更具有线性相关性。首先将不同运动数据分类,
并随机切片,每组数据有着不同的时间长,并求取每组数据的峰值平均加速度,平均温度、平均湿度、时间长度和能量消耗。
多元线性回归模型的一般形式为:
B=A1X1+A2X2+A3X3+…+AiXi+…+AjXj
(3)
式中:j为解释变量的数目,Ai(i=1,2,3,…,k)为回归系数。由(3)式表示n个随机变量的矩阵表达式为:
B=AX
(4)
其中A为

第一列为常数项,第二列为峰值均值加速度(m/s2),第三列为温度(℃),第四列为湿度,第五列为时间长度(min),B为能量消耗(kJ),选用移动端APP输出的能量消耗(1kcal=4.186kJ),移动端平台界面见图4。

图4 移动端平台界面
方程最优解为:
ATAX=ATB
(5)
由式(5)提取系数得:
X=(ATA)-1ATB
(6)
此时X即为此方程的最优解。
但由于实际的数据中矩阵A常会有接近的数据,存在接近奇异的矩阵,故本文在求矩阵的逆的时候用的是matlab中的pinv函数,pinv函数在矩阵是非奇异阵时会正常求逆,而到了接近奇异或者奇异矩阵时会求其伪逆,这样就可以求出系数矩阵X的最优解了。得到的结果如下:
(1) 慢走卡路里计算公式:
男:
Q=-831.906-1.9323×a-11.9552×T+24.1011×h+60.9750×t
(7)
式中:Q为能耗(kJ);a为平均加速度(m/s2);T为温度(℃) ;h为湿度(%);t为时间(min)。
拟合系数R2=0.9122
女:
Q=-174.9526+10.5600×a-4.4530×T+6.1074×h+18.1614×t
(8)
式中:Q为能耗(kJ);a为平均加速度(m/s2);T为温度(℃) ;h为湿度(%);t为时间(min)。
拟合系数R2=0.8119
(2) 快走卡路里计算公式:
男:
Q=2545.2625+12.1264×a+51.6791×T-83.9180×h+87.2568×t
(9)
式中:Q为能耗(kJ);a为平均加速度(m/s2);T为温度(℃) ;h为湿度(%);t为时间(min)。
拟合系数R2=0.9373
女:
Q=472.9824-1.7987×a+13.0394×T-17.7629×h+41.5996×t
(10)
式中:Q为能耗(kJ);a为平均加速度(m/s2);T为温度(℃) ;h为湿度(%);t为时间(min)
拟合系数R2=0.9613
(3) 慢跑卡路里计算公式:
男:
Q=-358.2458-0.5232×a-3.4442×T-9.2837×h+40.397×t
(11)
式中:Q为能耗(kJ);a为平均加速度(m/s2);T为温度(℃) ;h为湿度(%);t为时间(min)。
拟合系数R2=0.9740
女:
Q=113.5473+0.1482×a+4.7097×T-5.3400×h+26.1123×t
(12)
式中:Q为能耗(kJ);a为平均加速度(m/s2);T为温度(℃) ;h为湿度(%);t为时间(min)。
拟合系数R2=0.8814
(4) 快跑卡路里计算公式
男:
Q=-2019.9221-1.6953×a-48.8678×T+71.6040×h+36.8129×t
(13)
式中:Q为能耗(kJ);a为平均加速度(m/s2);T为温度(℃) ;h为湿度(%);t为时间(min)。
拟合系数R2=0.8837
女:
Q=-643.7273+1.8674×a-19.1150×T+25.0888×h+31.8023×t
(14)
式中:Q为能耗(kJ);a为平均加速度(m/s2);T为温度(℃) ;h为湿度(%);t为时间(min)。
拟合系数R2=0.9792
其中,拟合系数R2是指回归直线对观测值的拟合程度。拟合参数是评价线性回归的一种重要依据,计算公式如下:
(15)
R2最大值为1。R2的值越接近1,说明回归直线对观测值的拟合程度越好;反之,R2的值越小,说明回归直线对观测值的拟合程度越差。由表中结果拟合系数看出,拟合程度较好。经检验,该方程具有统计学意义(P<0.01),各片回归系数和截距也有统计学意义。
经对比证明,回归公式计算得到的卡路里消耗值与移动端APP实测卡路里消耗值基本一致。
4 结论
从男女分别在慢走、快走、慢跑、快跑四种运动状态下卡路里计算公式中可以看出,能量消耗与运动加速度、温度、湿度、运动时间是具有线性关系的。传统的运动能耗计算公式只考虑了运动步数,而人体运动是复杂多变的,其能量消耗还与运动强度、身体形态、运动时间、温湿度等参数的变化相关,仅仅通过计步来实现卡路里消耗的计算具有较大的误差。本研究出于能耗计量精度的要求,分别得出男、女各运动状态下的能耗计算公式之后,结合人体运动状态自动识别系统,可将复杂的运动细分归类到慢走、快走、慢跑、快跑四种强度的运动状态中,再分别进行对应卡路里消耗的运算,从而实现人体运动能耗的精确计算。另外,通过对男、女不同运动状态能耗算法的分别研究,我们发现性别差异对卡路里消耗具有较大的影响,其原因有待进一步研究。
参考文献:
[1] David Cuartielles Ruiz, Andreas Goransson. Android可穿戴设备高级编程[M]. 北京:清华大学出版社,2015: 203-204.
[2] Rodahl, K., Vokac, Z., Fugelli, P., Vaage, O. and Maehlum, S. (1974). Circulatory Strain, Estimated Energy Output and Catecholamine Excretion in Norwegian Coastal Fishermen. Ergonomics, 1974,17(5):585-602.
[3] 朱国忠,韦彩虹,潘敏.基于三维加速度传感器的人体运动能耗检测预算的研究[A],传感技术学报,2011,24 (8):1217-1222.
[4] 李丹,陈焱焱,姚志明等. 基于三轴加速度传感器的人体日常体力活动识别系统设计[J]. 仪表技术,2013(9):1-5.
[5] 朱弋,阮兴云,徐志荣,等. 身体运动加速度与运动量测量的关系研究[J]. 医疗装备.2003(8):9-10.
[6] 陈莉莉.基于重心位移监测的卡路里消耗计算算法[D],西南师范大学学报(自然科学)版),2016,7(41).55-60.
[7] 余杰,杨连贺,焦帅,等. 基于三轴加速度传感器的人体行为识别研究[J]. 软件工程.2016,19(9):34-37.
[8] 丁永生,吴怡之,郝矿荣,等.智能服装理论与应用[M].北京:北京科学出版社.2013.
