离心泵叶轮前间隙控制系统研究

汤 超，曾文平

（ 广州城建职业学院 机电工程学院，广东 广州 510900）

0．引言

离心泵是生产过程中一种输送液体的常见机械装置，泵的核心部件是叶轮[1]，在工作一段时间后，其与泵盖的间距即叶轮前间隙会发生一定的变化，而这会影响到泵的容积效率的改变。一般来说，间隙增大，泄露增加，工作效率降低，间隙变小，叶轮易与前泵盖发生接触摩擦，泵会受到磨损。因此，控制好叶轮前间隙显得很有必要。

目前调整叶轮前间隙方法比较单，即停机拆卸泵盖并重新调整安装叶轮，此方法的最大缺点是不能实时控制间隙且效率低下。目前国内外对于调整叶轮前间隙的研究还比较少[2-3]，对其实时控制更是鲜有研究，本文设计了一套调整叶轮前间隙的电液伺服位置控制系统以达到实时控制的要求。采用传统PID控制和二次型最优控制对电液伺服系统做对比仿真研究，最后根据控制效果选取最佳方案。

1．间隙调整装置设计方案

本课题研究的是离心泵前泵盖和叶轮之间的间隙调整，如果要实现实时控制调整此间隙需要对泵的结构做一定改造。主要有两种改造思路：一是保持泵盖位置不变，移动叶轮；二是保持叶轮位置不变，移动前泵盖。由于泵内部空间紧凑，结构较为复杂，相比选择第二种思路，因为改造前泵盖实现起来更为简单一些。改造方案如图1所示。

图1 间隙调整方案示意图Fig 1 Sketchmap of clearance adjustment scheme

由图1可知，采用液压驱动方式带动泵盖移动方案，在实际改造中是将传统前泵盖改进设计成带有变形液压缸的新型装置以实现所需功能。

2．建立间隙电液伺服控制系统数学模型

电液伺服控制系统由单片机、传感器、数模转换器、伺服放大器、伺服阀和特殊液压缸组成，其控制系统如图2所示。

阀控缸三个最基本的平衡方程描述了液压缸的动态特性[4]。对这三个等式做拉氏变换，得：

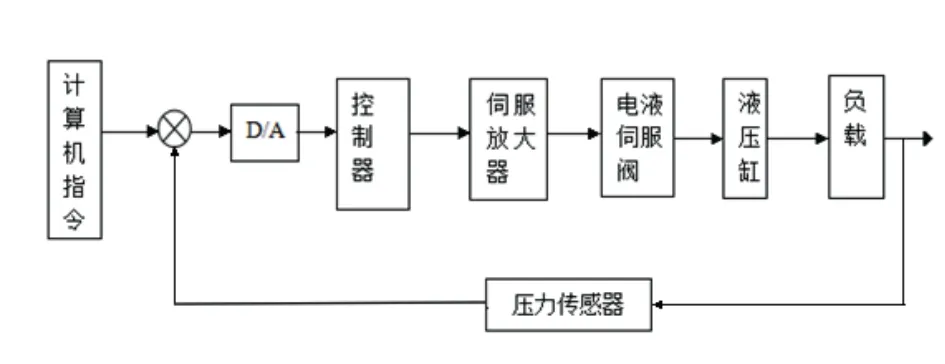
图2 调整装置液压控制系统框图Fig.2 Hydraulic control system diagram of adjusting device

根据图3可得调整装置控制系统开环传递函数为：

式（4）中：Kq—伺服阀的流量增益；Ka—伺服放大器增益；Ap—液压缸有效面积；—液压缸阻尼比；—液压固有频率。

图3 调整装置控制系统传递函数框图Fig.3 Control system transfer function diagram of adjusting device

离心泵叶轮前间隙电液伺服系统的参数如表1所示。将各参数代入（4）式计算，得系统开环传递函数（5）为：

则，系统闭环传递函数（6）为：

表1 电液伺服系统参数Tab.1 Parameters of electro-hydraulic servo system

3．间隙调整装置控制系统

3．1．间隙调整装置控制系统PID控制

PID控制是目前最常用的控制方法，将PID控制器引入到控制系统中[5]，对叶轮前间隙电液伺服控制系统进行仿真研究，结合MATLAB中SIMULINK模块建立间隙调整装置控制系统的PID控制模型，结果如图4所示。通过SIMULINK可得间隙调整装置控制系统PID控制阶跃响应曲线图（图5）。

PID的三个参数对于控制仿真结果有着直接影响，经过反复试凑调整，最终得到 KP=3，KI= 2.5， KD= 0.05。

由图5可看出，系统在8.8 s时达到稳定，最大超调量为25%，对于离心泵间隙控制系统来说达到稳定时间较长，需进一步改进控制效果。

图4 PID仿真模型Fig.4 PID simulation model

图5 PID仿真结果Fig.5 results of PID simulation

3．2．间隙调整装置控制系统最优控制

设线性时变系统的状态方程（7）为

二次型性能指标（8）

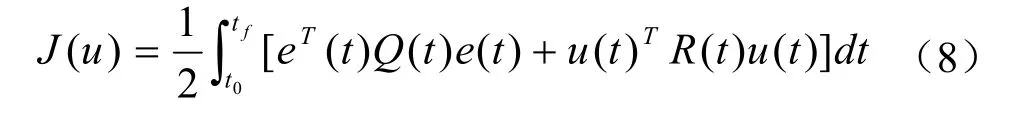
式（8）中：Q—半正定对称时变加权矩阵；R—正定对称时变加权矩阵。

Q，R是衡量误差分量和控制分量的加权矩阵，可根据各分量的重要性灵活选取。U(t)不受约束，最优控制核心问题就是求解U(t)使二次型性能指标最小，其表达式（9）为：

式（9）中K为反馈系数矩阵，P为Riccati方程的解

控制系统状态空间方程（11）为：

在MATLAB中应用Lqr()函数求解最优状态反馈矩阵K和Riccati方程的解P[6-9]，其基本调用格式为：

Q，R可取经验值，Q=diag([1010,0,0])，R=1，加入最优控制后系统状态方程（13）为：

式（12）中： K=［25 342892］

优化后的传递函数（15）为：

基于最优控制的间隙调整装置控制系统仿真结果如图6所示。由图6可看出，系统在0.4s内达到稳定，没有出现超调，稳态时间相比PID控制明显缩短，控制效果良好。

图6 最优控制仿真结果Fig 6 Simulation results of optimum control

4．结论

文中对离心泵叶轮前间隙调整装置控制系统进行研究，建立了间隙调整装置控制系统的数学模型，得出了该系统的PID控制和最优控制。仿真表明，相比于传统的PID控制，最优控制后的控制系统具有较好的跟随性，其响应速度明显加快，响应时间缩短了8.4 s。

参考文献：

[1]关醒凡．现代泵技术手册[M]．北京：宇航出版社，1995：24-26．

[2]赵卫星，赵磊．渣浆泵叶轮间隙的调整[J]．科技资讯，2006，18（35）：43-44．

[3]朱利英．脱硫循环泵叶轮间隙的调整[J]．通用机械，2011，4（3）：66-67．

[4]张利平．液压控制系统及设计[M]．北京：化学工业出版社，2006：45-47．

[5]黄俊年，王立．浅析PID控制原理及应用[J]．硅谷 ，2010，1（4）：109-110．

[6]姜洪发．基于MATLAB的倒立摆最优控制设计和仿真[J]．智能机器人，2016，10（5）：47-50．

[7]刘本学，蔺超云，郭沛东，等．基于MATLAB的汽车线性最优控制主动悬架仿真研究[J/OL]．郑州大学学报：工学版，2016，5（37）：72-76．

[8]蔡大伟．基于MATLAB的电液伺服系统线性二次型最优控制[J]．智能机器人，2016，6（6）：64-67．

[9]韩淑华，张玉宝．基于MATLAB的电液位置比例系统的最优二次型控制[J]．流体传动与控制，2008，3（4）：9-11．