钛合金热粘塑性本构关系的子程序开发及有限元验证

李云飞，曾祥国

(1.中国工程物理研究院总体工程研究所，四川 绵阳 621999)(2.四川大学，四川 成都 610065)

0 引 言

钛合金具有优良的力学性能以及耐腐蚀性能，在航空航天、海洋工程、石油化工等领域得到广泛应用。近年来，随着各工业领域对金属材料在极端服役条件下的性能要求愈加严苛，因此需要对钛合金等材料在高应变率、高温等载荷下的特性进行探究。

对于钛合金在高速冲击、碰撞等极端载荷下的力学行为，研究者提出了诸多热粘塑性本构模型，这些模型主要可分为2类。一类是通过大量离散实验数据拟合得到的唯象经验型本构模型，其中Johnson-Cook唯象本构方程的应用最为广泛，其流变应力-塑性应变关系式为[1-2]：

(1)

此外，针对Johnson-Cook模型在高应变率下无法准确描述材料流变应力下降趋势的缺陷[3]，一些学者提出了改良的物理本构模型。Zerilli与Armstrong[4]基于晶体材料塑性变形过程中位错运动的热激活机制，提出了可描述晶体结构分别为体心立方(bcc)与面心立方(fcc)的金属材料力学行为的本构模型，对于bcc金属材料：

(2)

对于fcc金属材料：

(3)

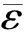
Gao 等人[5]基于金属塑性变形细观位错理论建立了bcc金属材料的塑性本构方程：

(4)

综上所述，实际上任何基于物理的或复杂的热粘塑性唯象经验本构模型，在同时考虑应变硬化、应变率强化以及温度软化效应时，其流变应力表达式都可写成以下形式[6]：

(5)

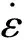
近年来随着计算机模拟技术的快速发展，利用有限元软件进行分析计算已成为现代科学研究中不可或缺的部分。相比ANSYS、MSC与AIDINA等通用有限元软件，ABAQUS对于计算不同材料、复杂载荷以及变化接触条件的非线性组合问题，尤其是非线性力学的分析求解功能处于世界领先水平。目前，虽然ABAQUS等通用有限元软件的材料库中自带了多种本构模型，但都无法准确描述材料在高速切削下的行为。而ABAQUS软件具备强大的自我扩展开发能力，为各专业领域的用户提供了若干子程序接口，允许将用户自定义的材料本构模型导入到软件的主程序中。

本研究则引入了一种显式积分算法，介绍了基于VUMAT子程序接口的将通用形式如式(5)的金属热粘塑性本构模型进行数值实现的具体方法，并基于Johnson-Cook模型编写VUMAT子程序对TC4钛合金的热粘塑性力学行为进行有限元模拟，对子程序的准确性与计算效率进行验证分析。

1 ABAQUS简介与子程序算法

1.1 ABAQUS动态分析技术

ABAQUS于1978年由有限元分析软件公司ABAQUS推出，被誉为国际上功能最强大的有限元分析软件之一，不仅可以进行静态分析，还可以准确分析碰撞、冲击、爆炸与断裂等瞬态问题，特别是在非线性分析领域可以解决复杂的工程力学问题。在结构、传热学、流体以及流固耦合、热固耦合等方面具有庞大求解规模的能力，在机械、土木、船舶、汽车、航空航天等各工程领域均发挥了巨大作用。

ABAQUS由ABAQUS/Standard、ABAQUS/Explicit和ABAQUS/CFD 3个主要分析模块组成，其产品模块如图1所示。在这3个模块中，Explicit可进行显式动态分析，它使用的显式求解算法特别适用于求解复杂非线性动力学问题。对于受冲击载荷并随后在结构内部发生复杂相互作用的结构瞬态响应问题可以很好的模拟。因此本研究选用ABAQUS/Explicit模块中的VUMAT接口进行子程序的开发与应用。

图1 ABAQUS产品模块示意图Fig.1 Schematic diagram of ABAQUS product modules

1.2 应力更新算法及VUMAT子程序

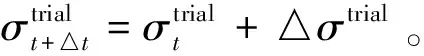
(6)

由式(6)可知该算法没有迭代积分，计算中只需要恒定的弹性张量De，可以显著减小计算量，提高计算效率。

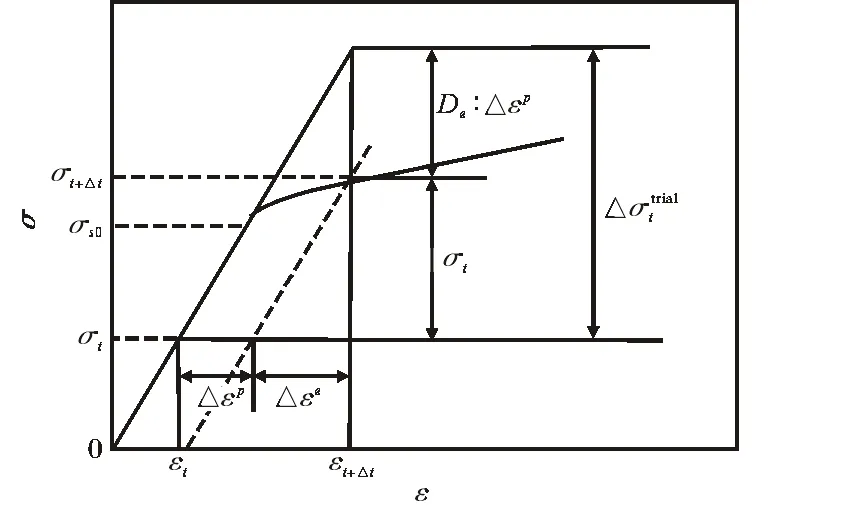
图2 应力补偿更新算法示意图Fig.2 Schematic diagram of stress compensation updating algorithm

显式积分算法基本控制方程及主要步骤如下，弹性变形过程，将应力写成应变率形式，则广义胡克定律为：

(7)

对于各向同性硬化的塑性流动采用Mises屈服准则，屈服方程为：

(8)

在某一增量步开始时，假定所有应变增量△ε均为弹性应变，则试应力σtrial写为：

(9)

(10)

(11)

(12)

为了满足实际工程应用，ABAQUS为用户提供了若干用户子程序(User Subroutines)接口，与命令行形式的程序格式相比，用户在子程序的限制少得多，功能强大，更加灵活方便。用户可以利用用户子程序UMAT与VUMAT接口自行定义材料的本构模型和有限元算法，其中，显式用户程序VUMAT适用于ABAQUS/Explicit中。VUMAT主要由以下几部分组成：子程序初始变量定义、调用ABAQUS外部材料参数、应力应变等参数更新主体程序、结束语句。

考虑到ABAQUS软件的材料库中自带Johnson-Cook模型，为了便于对比验证子程序的可行性与准确性，本研究以采用Johnson-Cook模型为例，编制其相应的VUMAT用户子程序。根据上述的应力补偿更新算法，定义了3个需要不断更新的状态变量，即等效塑性应变、等效塑性应变率与流变应力。实现Johnson-Cook本构方程的子程序主要计算步骤如下：

(3)调用子程序，计算初始流变应力σf；

(4)将试探应力代入屈服判断准则，判断是否发生屈服；

(6)若屈服，计算本增量步的塑性应变增量△εp，利用应力补偿更新算法更新本增量步结束时的应力；

(7)更新内能、消耗的无弹性能、各状态变量的值；

(8)结束，返回主程序。

VUMAT子程序的计算流程如图3所示，子程序在每一个材料积分点被ABAQUS主程序调用[9-10]。

2 结果与分析

图3 VUMAT子程序计算流程图Fig.3 Flowchart of VUMAT subroutine

根据上述显式积分算法以及简化的应力补偿更新算法，按照ABAQUS用户子程序接口规范，基于FORTRAN语言编写Johnson-Cook本构模型的VUMAT子程序。数值模拟中的材料选用TC4钛合金，其本构参数如表1所示。考虑到材料行为与结构形态无关，在ABAQUS中采用单个八节点六面体等参单元(C3D8R)对TC4钛合金在单轴加载条件下的应力应变响应进行了数值模拟。测试单元的边界条件及载荷如图4所示。

表1 Johnson-Cook动态本构参数优化值

图4 测试单元的边界条件与载荷Fig.4 Boundary and loading condition of testing unit

在ABAQUS/Explicit中调用VUMAT用户子程序，分别得到TC4钛合金在不同应变率(1、10、100、1 000 s-1)及不同温度条件(293、323、353、403、503 K)下的应力-应变响应曲线如图5、图6所示。由图可知，TC4钛合金的塑性流变应力随应变率的增大而逐渐增大，随初始温度的升高而逐渐降低，可见VUMAT子程序能够较好地描述钛合金或其他金属的应变率强化与温度软化效应，验证了子程序显式积分算法的可行性。

图5 不同应变率下TC4钛合金数值模拟应力-应变曲线Fig.5 Simulation results of TC4 titanium alloy under different strain rates

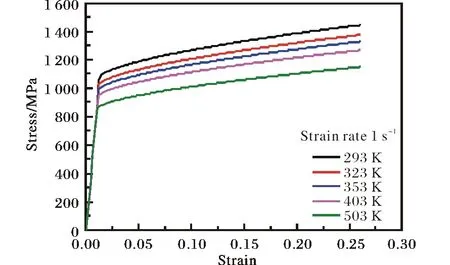
图6 不同初始温度下TC4钛合金数值模拟应力-应变曲线Fig.6 Simulation results of TC4 titanium alloy under different initial temperatures

为了验证VUMAT子程序对TC4钛合金本构行为预测的准确性，在ABAQUS/Explicit中调用子程序，得到不同应变率、不同初始温度条件下的应力-应变曲线，其与文献[11]的实验数据对比结果如图7所示。由图可知，子程序数值模拟结果与实验数据吻合良好，可见该子程序可以较好地描述TC4钛合金在不同载荷条件下的本构行为，该显式积分算法可以推广至其他用户定义的金属热粘塑性本构模型的数值应用中。

图7 不同应变率下TC4钛合金数值模拟结果 与实验结果的对比Fig.7 Comparison between simulation results and experiment results of TC4 titanium alloy under different strain rates

以上为对单个单元本构行为的验证，对于结构的准确度以及计算效率的验证，本研究选择平面应变悬臂梁的实例，调用VUMAT子程序进行数值模拟，然后与采用ABAQUS自带的Johnson-Cook模型模拟结果进行对比。悬臂梁长度为1 m，高度为0.2 m，左端固支约束，右端载荷为一垂直向下的高速冲击位移载荷0.1 m，载荷时间为0.01 s。悬臂梁材料选用TC4钛合金。子程序与软件自带Johnson-Cook模型的数值模拟Mises等效应力结果对比如图8所示。两者最大等效应力的误差约为2.4%，可见子程序与ABAQUS自带模型的计算结果吻合较好。然而，子程序的计算时间为21 s，自带Johnson-Cook模型的计算时间为230 s，可见VUMAT子程序的计算效率明显优于自带模型。

图8 子程序与自带模型等效应力数值模拟结果对比Fig.8 Comparison of Mises stress calculated with subroutine(a) and ABAQUS’s own model(b)

3 结 论

本研究基于显式应力积分算法将用户自定义的金属热粘塑性本构模型通过VUMAT子程序进行了数值程序实现，解决了商业软件中自带模型无法描述材料在高速切削等条件下力学性能的问题。与实验数据对比发现，子程序能够较好地描述TC4钛合金或其它金属的应变率强化与温度软化效应。同时通过与ABAQUS软件自带的Johnson-Cook本构模型数值模拟结果对比发现两者结果吻合良好，子程序在计算效率方面与前者相比有较大提高。该子程序研究可为钛合金等金属高速碰撞冲击、切削或爆炸变形等情况的数值模拟提供技术支撑。

[1] Johnson G R, Cook W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics, 1985, 21(1): 31-48.

[2] 杨扬, 曾毅, 汪冰峰. 基于Johnson-Cook模型的TC16钛合金动态本构关系[J].中国有色金属学报, 2008, 18(3): 505-510.

[3] Arsecularatne J A, Zhang L C. Assessment of constitutive equations used in machining[J]. Key Engineering Materials, 2004, 274-276:277-282.

[4] Zeriili F J, Armstrong R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations[J]. Journal of Applied Physics, 1987, 61(5):1816-1825.

[5] Gao C Y, Zhang L C, Yan H X. A new constitutive model for HCP metals[J]. Materials Science and Engineering A, 2011, 528(13/14): 4445-4452.

[6] 彭鸿博, 张宏建. 金属材料本构模型的研究进展[J]. 机械工程材料, 2012, 36(3): 5-10.

[7] 李云飞, 曾祥国, 盛鹰,等. 基于实验的钛合金优化动态本构模型与有限元模拟[J]. 材料导报B:研究篇, 2016, 30(12): 137-142.

[8] 李宏伟.宏细观本构关系数值化及其在有限元模拟中的应用[D].西安:西北工业大学, 2007.

[9] 兰彬, 叶献辉, 宋顺成, 等. 304NG不锈钢高应变率材料模型在ABAQUS 中的实现技术[J]. 应用数学和力学, 2015, 36(2): 167-177.

[10] 刘洋, 王秀梅, 王幸敏，等.基于VUMAT的钛合金切削仿真[J]. 工业控制计算机, 2016, 29(8): 19-21.

[11] Khan A S, Suh Y S, Kazmi R. Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys[J]. International Journal of Plasticity, 2004, 20(12): 2233-2248.