主动式双目视觉三维成像技术研究

牟科瀚，王泽勇

（西南交通大学物理科学与技术学院光电工程研究所，四川成都，610031）

0 引言

光学三维测量分为被动三维测量技术和主动三维测量技术两大类。被动测量技术在照明方式上不需要借助结构光的照明，可以从一个或多个现成的摄录系统中直接使用已经捕获到的二维数字图像中还原出物体的形貌。主动测量技术需要结构光的照射，从携带有待测物体表面三维形貌信息的数字图像中，通过一些别的算法得到待测物体的三位形貌。

双目视觉是基于人眼成像理论的被动三维成像技术。它是基于视差原理，利用成像设备从不同位置获取被测物体的两幅图像，通过图像对应点之间的关系，来计算三维信息的[1]。其具有效率高、精度合适、系统结构简单、成本低等优点，非常适合于制造现场的在线、非接触产品检测和质量控制系统。由于图像获取是在瞬间完成的，因此是一种有效的快速三维测量方法。

铁路在我国经济社会发展中的地位和作用至关重要。为了使列车走行部在运行时保持良好的状态，需要在列车行驶前对走行部进行细致的检查工作，以满足列车安全行驶条件[2]。在日常的一级检修过程中，通常是使用目视、人工的方式来进行检查，这样的方式费时费力，列车需要在动车段或机务段停留很长时间完成检测，同时车底部件繁多，环境黑暗，对检修员的安全也造成了威胁[3]。因此，为了节省检测时间、保证检测安全，需要设计一个图像检测方案，使检测员可以直接在电脑端上观察车底部件的三维图像。

一个完整的双目立体视觉系统主要有一下六个部分组成：（1）摄像机标定；（2）图像获取；（3）特征提取；（4）立体匹配；（5）深度计算；（6）内插与重构[4]。针对这六个步骤，国内外学者进行了大量的研究，以提升双目视觉测量效果。

本文基于SIFT双目匹配，进行了双目三维成像技术研究。针对双目视觉的匹配难问题，通过引入结构光投影的方式作了改进，大幅度提高了匹配精度，对三维成像效果有较大提升。将该双目三维成像的方式用于的列车底的部件检测，进行了三维成像验证。

1 双目视觉模型

双目视觉三维成像的数学模型如下图所示。为了数学推导的简便，这先做两个假设：①透镜成像无畸变；②两摄像机成像是行对准的。基于这两个假设，得到空间点P( X, Y, Z)的深度与该店在左右视图中的坐标点和的数学关系。

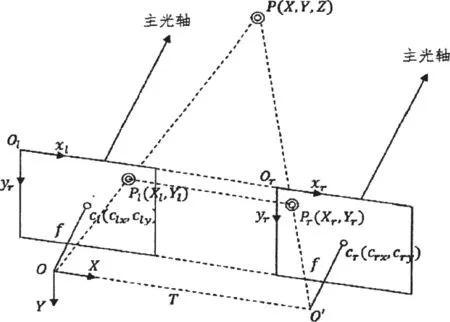
图1 双目视觉系统数学模型

下面基于以上两个假设，进行数学推导。

假设 P( X, Y, Z)为空间中的待测点，其在左右相机中的成像点分别为两摄像机的主点分别为注意，主点是主光线与像平面的交点，该交点在镜头的光轴上。由于机械安装无法保证镜头光轴与CCD成像中心法线完全重合，所以像主点并不与图像中心完全重合，即Cl和Cr并不是左右视图的中心点。

三组比较，年龄、性别、受教育年限、糖尿病病程、BMI、空腹血糖、C肽、血脂差异均无统计学意义（P＞0.05）。与Non-DPN组相比，Painful DPN组有更低的HbA1C（P＜0.05）。三组患者MoCA评分差异均无统计学意义（P＞0.05）。与Non-DPN组相比，Painful DPN及Painless DPN组SDS、SAS、SRSS得分均显著增高（P＜0.05，表1）。

在图中共有三个坐标系： xlolyl， xroryr和XOY。为 左 摄 像 机 的 坐 标 系， 其 中为ol坐标原点。 xroryr为右摄像机的坐标系，其中，以or为坐标原点。XOY为世界坐标系，其中P( X , Y, Z)以O坐标原点。

根据三角形相似原理，我们可以得知： ∆P PlPr～ ∆P OO′。

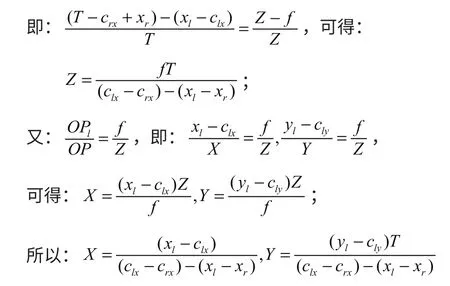
那么将物理世界中的点投影到摄像机上，可以用下式表示：a=QA

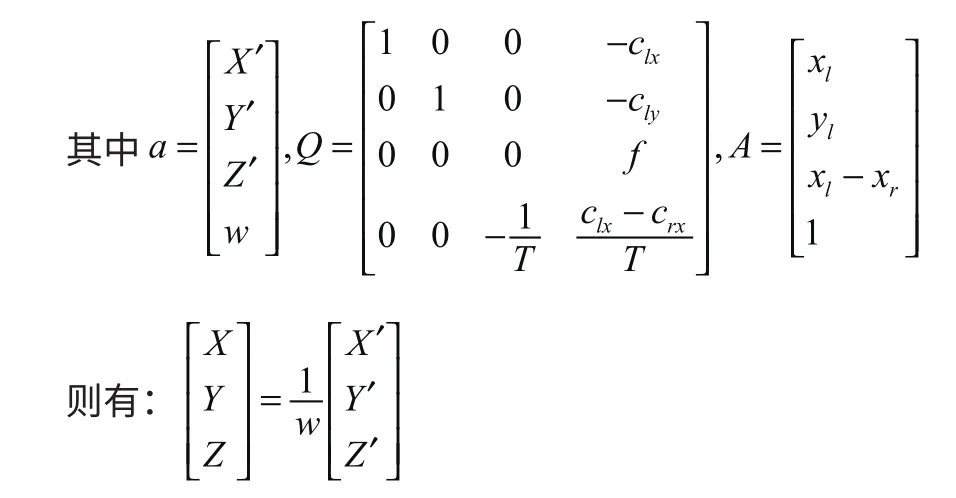
需要注意的是，实际情况是两摄像头的水平中心距应写为Tx,此处为假设条件下的简化推导，世界坐标系的X轴就取在OO′上，所以Tx=T。

xl, xr分别是P点在左右摄像机的成像视图上的水平像素位置，其差 xl−xr即为通常所说的视差，由于待测物体的多样性与复杂性，求取视差往往成为整个三维成像中的关键点。

结合相机畸变，根据针孔相机模型，物体目标世界坐标点与计算机图像上对应像素点之间的关系如下：

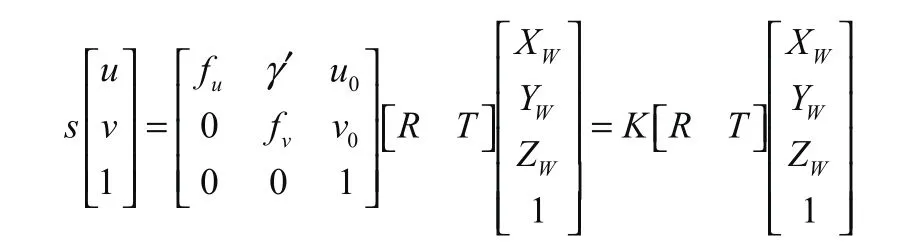
其中：K为相机内参矩阵；

R =[r1r2r3]为相机的旋转矩阵；

T为相机的平移向量。

上式中内参矩阵包含了相机的焦距、畸变等信息，而双目相机的旋转、平移等信息则包含在外参矩阵中。将内参矩阵与外参矩阵整合，可得到下式：

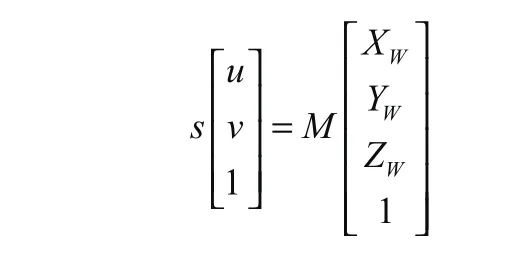
其中M为投影矩阵（又称为单应性矩阵）。

该式子展开可以得到3个线性关系式，消除尺度因子s后留下两个关系式，而未知量有3个，所以至少需要两台相机才可以完成深度的测量。

2 SIFT特征匹配算法

SIFT的全称是Scale Invariant Feature Transform，尺度不变特征变换，由加拿大教授David G.Lowe提出的。SIFT特征对旋转、尺度缩放、亮度变化等保持不变性，是一种非常稳定的局部特征。该算法首先建立图像的尺度空间描述，通过高斯微分函数来识别潜在的对尺度和选择不变的极值点，根据其局部的梯度方向，建立特征描述向量，是一种具有放缩、旋转和仿射不变性的特征检测描述方法。

将图像I与不同高斯核的二维高斯函数G做卷积得到不同尺度下的尺度空间L，两两相减得到高斯差图像D( x, y, )，其中的每个像素与它的上层、下层以及邻域共26 个像素点做灰度值的比较，将最大或者最小值作为候选特征点。为了增强匹配的稳定性还需要在候选特征点中去除低对比度的极值点和不稳定的边缘响应点，从而精确定位极值点获得局部特征点。

以每个局部特征点为中心，在其邻域取 16×16的窗口，划分为 4×4 的像素块，在每个像素块上计算 8 个方向的梯度直方图分属 8 个区间，每个区间的值为各个梯度幅度的高斯加权后的累加值。因此每个 4×4 的像素块都可以用一个长度为 8 维的描述向量来表示，这样每个局部特征点就会产生一个长度为 128 的 SIFT 特征向量。将特征向量长度进行归一化处理，进一步去除光照的影响。

特征向量的匹配就是通过计算待匹配的两幅图像中局部特征点的欧氏距离对SIFT特征向量进行相似性度量，即查找第一幅图像的每个局部特征点在另一幅图像中的最近邻。设定比例阈值R, 0

3 实验验证

■3.1 双目三维成像实验

在进行三维成像前，需要先对双目相机进行标定，即计算出相机的单应性矩阵。本文采用张正友标定法。标定用棋盘格如图2所示。

计算得到相机参数：

图2 相机标定棋盘格

完成了相机参数标定后，通过双目相机采集到的两幅图像，如图3所示。

图3 待测部件图像对

图中为列车车底部件，整体环境偏暗，大量平面区域，可提取的特征点较少。直接对图像进行双目匹配，结果如图4所示。

图4 双目匹配结果

从匹配结果可以看到，在平面区域有大量未匹配的空隙，未能达到三维成像的标准。为了提高匹配效果，增加特征点，此处引用了结构光投影。投影图像为随机散斑，如图5所示。

图5 散斑投影部件图像对

对投影后的图像进行双目匹配，得到的结果如图6所示。

图6 双目匹配结果

比较之前未投影图像的匹配结果，可以发现投影了随机散斑的图像几乎匹配完全，结合相机标定参数即可进行三维重构，结果如图7所示。

图7 三维形貌复原

可以看到，该方法取得了很好的恢复效果。

■3.2 与傅里叶轮廓术对比实验

傅里叶轮廓术，是一种主动式三维测量技术。利用快速傅里叶变换计算光栅条纹图像的频谱，经过滤波处理后，从频谱中提取出被测物体表面的相位值，进而计算出物体的三维外形数据。

双目三维成像其关键因素在于匹配点的精确度与亢余度，在特征点较多，类似于边缘处其复原结果较好，而特征点较少的平面处（连续光滑面，如车轮踏面），恢复的三维图像会比较稀疏其有一定的杂点产生，这是由于匹配的不准确造成的。而傅里叶轮廓术，由于光栅的周期特性，在处理相位截断区域（实际物体中的不连续部分，如截面、断面处）是不准确的，该方法在针对连续面，如车轮踏面，有较好的恢复效果，当区域内部件较为复杂时，就不能得出准确的三维图像了。总体而言，双目视觉有着更加优越的成像性能。

4 总结

本文从双目视觉的数学模型出发，推导了相机坐标系与世界坐标系之间的关系。利用SIFT匹配算法进行了双目三维成像。针对匹配过程中，特征量少、匹配结果差难以进行三维成像的问题，引入了主动式投影。通过投影随机散斑的方式，增加了匹配特征，从而使匹配质量大幅度提升。最后针对列车走行部的部件进行了三维成像实验，取得了较好的成像结果。并于主动式三维成像技术中的傅里叶轮廓术作了对比实验，实验结果表面采用了结构光投影的双目三维成像有着更好的效果。

* [1]陈济棠.双目视觉三维测量技术研究[D].广东工业大学，2011

* [2]王明慧.高速铁路质量安全事故案例[M].西南交通大学出版社，2014

* [3]吴应永.基于SIFT的火车车底螺栓图像识别技术研究[D].西南交通大学，2016

* [4]罗佳娥.双目立体视觉深度感知与三维重建若干问题研究[D].中南大学，2012