基于盲反卷积的超声合成孔径图像复原

孔垂硕，罗林，李金龙，高晓蓉

（西南交通大学物理科学与技术学院，四川成都，610031）

1 盲反卷积原理

本文中使用了合成聚集（SF）成像方法，合成聚焦成像的基本原理见图1，第一次激发第1个阵元发射，全部孔径接收；第二次激发第2个阵元发射，全部孔径接收，以此类推，直到第N次激发最后一个阵元发射，全孔径接。

图1 合成聚焦成像原理

对于扫查区域内的某一点目标 P( r ,θ) ，根据合成聚焦法得到的点目标 P( r ,θ) 的叠加信号 s( r ,θ) 为：

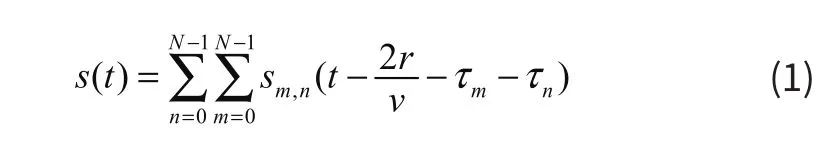
式中，τn为第n个阵元发射时的延迟时间。τm为第m个阵元接收时的延迟时间。r为成像点 P( r ,θ) 与原点O的路径距离，夹角为θ。

对于一组A扫信号s( t)可以表示为：

式中：h( t)为信号传播路径（包括电气系统）冲击响应函数，超声反射系数分布信息r( t)，n( t)为检测噪声，＊为卷积符号，式（2）变表征了超声检测回波信号形成的线性数学模型，为了获取r( t)的最优估计以提高检测分辨率，因此有必要采用盲反卷积的技术消除h( t)的影响。根据贝叶斯理论，在测量数据条件下，估计参数和的概率为：

其对数形式为：

根据最大似然估计原理，盲反卷积简述为：从测量数据中估计出目标函数和冲击脉冲响应，使似然函数最大化，即盲反卷积是似然函数的最优化过程。

通过交替迭代式（7）和式（8）一定次数后，似然函数趋向最大化，可以分别得到冲击脉冲响应函数和原始信号的估计，但是由凸集投影理论可知，如果不施加一定的约束条件，算法并不能保证收敛到全局最优解，有可能只有一个局部极值解。在每次迭代之后，需要对新的冲击脉冲响应及原始信号估计进行限制，具体的约束条件包括:（1）单位和约束：该约束为了保证迭代过程中信号能量保持不变；（2）带宽限制：在频域截止频率以外，有 Hn+1(t)，因为初始冲击脉冲响应函数具有一定的频率限制，因此需要在迭代过程中添加约束保证冲击脉冲响应函数的频率不变。

2 仿真和实验

■2.1 仿真实验结果

采用FieldⅡ仿真单个散射点的探头阵列、发射信号和成像区域参数以及散射点位置信息，相关信息见表1，成像过程建模用到的初始的系统冲击响应函数为高斯脉冲函数，其有效部分和对应频谱如图2所示。

表1 单点仿真参数

图2 初始的冲激响应函数及其频谱

图3为仿真单个缺陷点而得到的结果，由Field II依据表1参数仿真A扫数据，由合成聚集成像算法合成原始图像a，利用预设的系统冲击响应函数与仿真产生的A扫数据卷积后形成退化的A扫数据，再由合成聚集成像算法合成仿真图像b，图c和图d分别使用盲反卷积信号复原算法迭代10次和20次合成后的图像，通过计算4幅图像中缺陷点的横向分辨率，比较成像质量来评价盲反卷积信号复原算法的有效性。

计算图3中四副图像的横向分辨率，a,b,c,d四副图像的横向分辨率分别为：0.52mm, 0.70mm, 0.67mm,0.63mm,四幅图相互比较我们可以计算出：图c中缺陷点的横向分辨率与图b相比提高了4.4%，图d中缺陷点的横向分辨率与图b相比提高了10.9%，经盲反卷积信号复原算法对退化后的A扫数据处理后，所合成图像中缺陷点的横向分辨率更高，由此可证明该算法在提高合成孔径图像分辨率的有效性。

图3 仿真单点超声合成孔径成像

图4为仿真两个缺陷点所得到的结果，其中缺陷点相距0.64mm，同样由Field II依据表1参数仿真A扫数据，由合成聚集成像算法合成原始图像a，利用预设的系统冲击响应函数与仿真产生的A扫数据卷积后形成退化的A扫数据，再由合成聚集成像算法合成仿真图像b，图c和图d分别使用盲反卷积信号复原算法迭代10次和20次合成后的图像。

图4 仿真两点超声合成孔径成像

计算图4中四副图像的横向分辨率，a,b,c,d四副图像的横向分辨率分别为：0.75mm, 0.82mm, 0.80mm,0.77mm,四幅图相互比较我们可以计算出：图c中缺陷点的横向分辨率与图b相比提高了2.5%，图d中缺陷点的横向分辨率与图b相比提高了6.6%，同时由图3可知，与图b相比，图c和图d中噪声更低，因此可证明，盲反卷积信号复原算法能够提高多目标合成孔径图像的分辨率，同时提高图像信噪比。

■2.2 实验结果

实验数据由Muilt2000多路便携式超声实验系统装置采集，实验所用试块及相控阵探头见图5。

图5 实验中所用试快及相控阵探头

实验信号相关参数如下：在实验过程中，发射信号采用中心频率是5MHz 的高斯调制信号，且接收信号的采样频率是100MHz。超声在实验试块中的传播速度为5930m/s，表2是相控阵探头阵列、成像区域参数以及缺陷点位置信息。

表2 阵元及成像区域参数

图6为单点实验数据超声合成孔径成像结果，实验平台采集数据经合成聚焦成像算法合成后得到图a，对采集到的A扫数据经盲反卷积信号复原算法分别迭代10次，15次，20次得到图b，c，d。

分别计算图6中四副图像的横向分辨率，a,b,c,d四副图像的横向分辨率分别为：0.82mm，0.79mm，0.73mm，0.70mm，四幅图相互比较我们可以计算出：经盲反卷积信号复原算法处理恢复后，图像中缺陷点的横向分辨率小于原始合成孔径超声图像，说明该算法能够提高对于实验数据缺陷点的横向分辨率。对比不同迭代次数下的横向分辨率，迭代10次，15次及20次横向分辨率分别提高3.7%，10.9%及14.6%，因此选用适度的迭代次数，对提高横向分辨率也是非常重要。

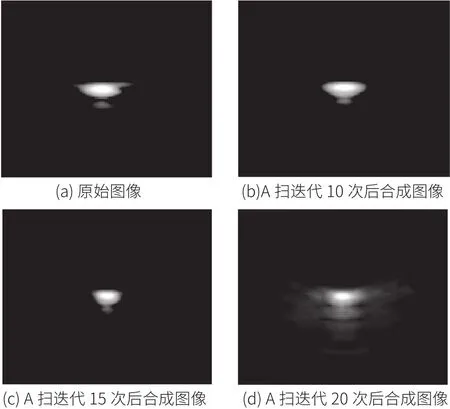
图6 单点实验数据超声合成孔径成像

3 结束语

本文提出利用盲反卷积信号复原算法重建超声合成孔径信号，以提高超声合成孔径图像分辨率，该方法根据最大似然估计原理，形成了超声合成孔径信号盲反卷积复原数学模型，通过迭代计算求得使似然函数最大的解，仿真和实验结果表明，该方法对合成孔径超声图像中缺陷点横向分辨率提高在5% 以上，同时选用适度的迭代次数，对提高横向分辨率也是非常重要。将盲反卷积算法使用到合成孔径超声信号复原中，可有效改善合成孔径检测图像分辨率，提高缺陷的检测质量。

* [1]孙宝申，沈建中.合成孔径聚焦超声成像(二)[J].应用声学，1993(3):39—44.

* [2]Lingvall F, Olofsson T. On Time—Domain Model—Based Ultras onic Array Imaging[J]. IEEE Transactions on Ultrasonics Ferroe lectrics & Frequency Control, 2007, 54(8):1623—33.