基于DCT的数字图像水印技术研究
2018-05-03张晓琪唐天国胡振杨华周金容
张晓琪,唐天国,胡振,杨华,周金容
(南充职业技术学院电子信息工程系,四川南充,637000)
数字水印技术[1]就是通过一些算法,将一些标志性的信息(包括多媒体、文档、软件等), 嵌入到数字产品中,并且不被感知,同时也不能破坏数据的正常使用和原有价值,以达到保护版权及合法利益的目的。图像数字水印大致可分空间域、变换域两类,当前比较多的新水印算法主要是基于变换域的,变换域算法相比空间域算法尤其是DCT域具有如下特点:一是变换域能与现有的图像压缩标准兼容,二是变换域可以有效与人类视觉系统的某些特征相结合,加之DCT域计算复杂性较低,研究DCT域水印算法成为热点。
本文给出了一种基于DCT域的数字图像盲水印算法,算法以离散余弦变换理论为基础,通过对原始图像的分块变换,选择中频系数,将有意义的二值水印图像嵌入到被保护的作品图像中,并实现水印的盲提取,利用MATLAB 工具软件仿真实验,并对嵌入水印的图像进行抗攻击测试,验证该算法具有较好的不可见性和较强的鲁棒性。
1 数字水印基本原理
数字水印的基本原理就是将具有特殊意义的一些标识信息,通过某些算法嵌入数字作品中,并且被嵌入的水印信息不会被感知,保证安全性。水印信息可以是随机序列、文本、图像、音频和视频等的任一种类型。本文研究的对象是静态图像水印。常用典型的数字图像水印技术主要包含两个基本系统即水印嵌入系统和水印提取(或检测)系统。
■1.1 数字水印的嵌入算法
数字水印的嵌入[2]是在密钥的指导下,将水印序列根据嵌入算法加入到原始图像的数据中, 根据图像情况也可以先将原始图像变换(例如傅里叶变换、离散余弦变换、小波变换等),再用水印序列改变系数,然后经过反变换重构含有水印的图像,典型的数字水印的一般模型如图1所示。
为了保证水印图像的安全性和鲁棒性,在实际应用中,常会对数字水印图像进行加密处理或随机预处理。假设I为原始载体图像,W为水印信号,K为密钥,w’为预处理的水印,可以由函数F定义为:
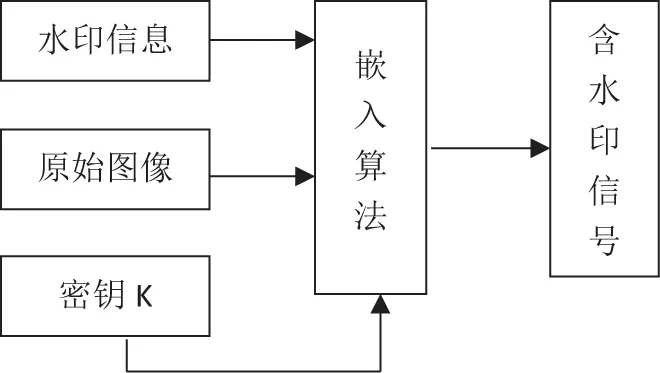
图1 水印嵌入算法框图

在嵌入水印的过程中,如设E为编码函数,I为原始的载体图像,被预处理过的水印图像为W’,含水印的载体图像IW则可表示为:
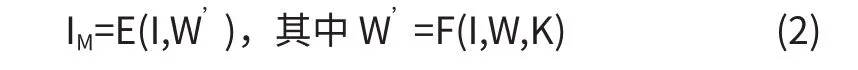
在嵌入水印信息的过程中,常用的嵌入算法有加性和乘性规则,可表示为:

其中:I(K)表示嵌入前频域系数,I’(K)是修改后的频域系数,a是嵌入的强度因子, w(k)表示第k个信息位水印。
■1.2 数字水印的提取算法
数字水印提取模型与嵌入模型对应,利用待检测图像和密钥提取水印序列(无论有无水印,都将按照提取算法提取),然后与原始水印序列进行比较,判断有无水印,典型的数字图像水印提取(或检测)算法如图2所示。
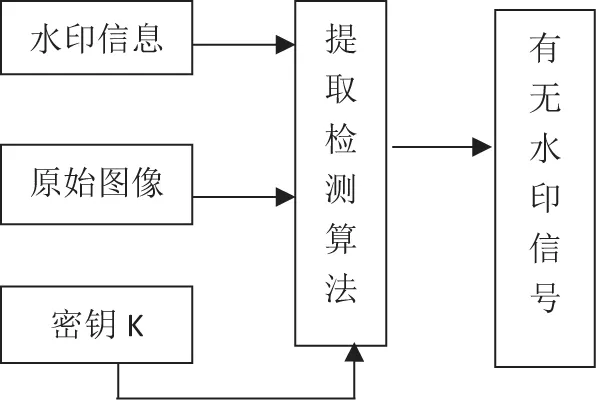
图2 水印提取算法框图
在数字水印系统中,水印的提取与水印的嵌入算法都很重要,如果对水印的提取过程定义为解码函数P,则可以通过1和0 来决策水印信息的有无,以此判定输出水印信息是否存在。同样设I为原始载体图像, Iw为嵌入水印的图像,有表达式如下:

其中,W表示提取的水印,K为密钥,a表示决策参数,C为相关检测函数,该函数是构建水印有效框架最为简便的方法,检测的输出结果就是数字作品版权的保护证据来源。
2 离散余弦变换(DCT)
离散余弦变换(DCT)[3]是一种实数域变换,常应用于数字信号处理的线性变换,能使二维信号的相关特性得到很好体现,DCT变换后能量聚集,具有很好的能量压缩与去相关能力。计算速度较快,在数字信号压缩和图像压缩等领域得到广泛应用。同时图像的JPEG 压缩标准以DCT 变换为基础,水印算法抗攻击JPEG 压缩的能力极大增强,因此DCT域变换在数字水印技术中受到青睐。
经过DCT 正变换,将二维图像分解到一组不同的空间频率上,则通过反变换将不同空间频率上的各个分量合成原始图像。数字图像处理中常使用的都是二维 DCT 变换。设一幅M×N的图像,其二维离散余弦正变换定义如下:
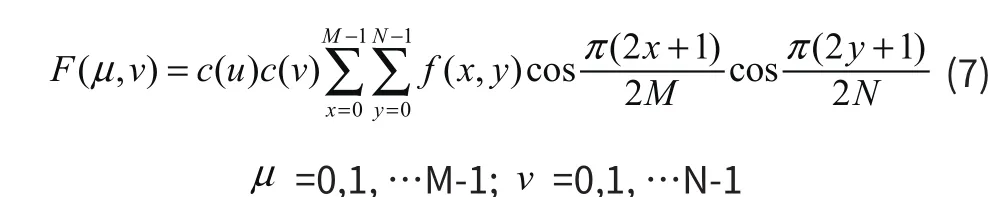
其中:
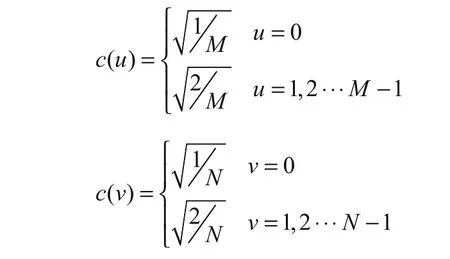
二维离散余弦反变换公式为:
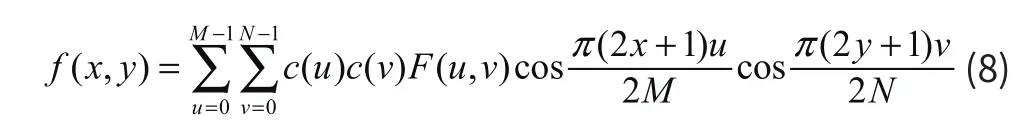
其中: x = 0,1 ⋅⋅⋅M − 1;y = 0,1 ⋅⋅⋅N − 1;x,y为空间的采样值,u,v为频域的采样值。
经过DCT域变换, 在低频部分主要集聚了图像的绝大部分能量,会有很高的压缩编码效率,通过直方图统计意义表明,系数值均集中在0附近,动态范围较小,DCT系数可用较少的量化比特数来表示,将水印信息嵌入到载体图像的中低频部分,能较好的抗JPEG压缩,如与空间域相比,它能嵌入的信息更多,并且有较好隐蔽性,鲁棒性也比较高。算法的性能结合人体视觉模型可进一步改进。
3 一种DCT图像数字盲水印算法与实现
盲水印算法是指在水印的检测过程中只需要密钥,不需要原始图像数据的参与。有效的节省了存储空间,使得其应用范围更加广泛。本文选择了性能较优的盲水印算法。
图像信号经过 DCT 变换后得到的系数分为DC(直流)系数和AC(交流)系数,并将AC系数从左上到右下分为了低频、中频、高频系数。由于DOC变换主要能量被压缩到了左上角低频系数中,载体的低频信息主要反应了载体的轮廓,不会有较大的失真。如果仅考虑鲁棒性,低频系数合适用来嵌水印入,但同时需要考虑水印的嵌入强度,否则会导致块效应,影响水印的不可见性。高频信息人类感知系统不敏感, 如果只是从水印不可见性角度考虑,高频系数比较适合嵌入水印,但鲁棒性相比较弱,将水印嵌入到高频部分,容易因量化、图像压缩、低通滤波等处理而丢失信息,影响水印的鲁棒性。因此,中频系数为较好的折中,达到最佳平衡的透明性和鲁棒性。本文选择中频系数嵌入水印信息。
■3.1 Arnold 的置乱变换
首先对水印信息进行预处理置乱变换加密,加密后再进行水印嵌入,可提高水印算法的安全性。对于二维的数字图像,Arnold变换[4]就是将数字图像的像素元素位置进行重新排列,使图像变得杂乱无章,获得混乱的图像,以达到隐藏图像信息的目的。
设水印图像 W 为 N×N 大小,则Arnold变换公式为:
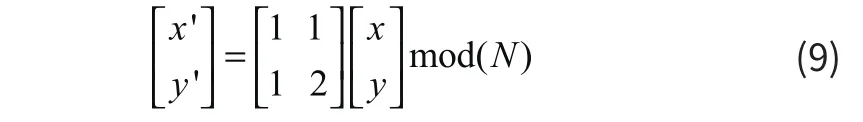
其中x,y∈{0,1,…,N-1},表示数字水印图像的像素坐标;x′,y′表示经过置乱后像素点的坐标;N表示方形图像大小,又称阶数。利用公式对图像的像素点逐一做变换,当遍历了图像所有像素点以后,将产生置乱加密的水印图像。
■3.2 水印嵌入算法
设原始载体图像为灰度图像,嵌入的水印信息为二值图像,利用对 DCT 系数关系的比较方法[5]嵌入水印信息。算法的主要思想是:将载体图像分成若干个8×8大小互不覆盖的子块,对每个子块进行 DCT 变换,在中频部分选择一个点作为嵌入位置,然后计算该点相邻6个坐标系数的平均值 aver,设α为嵌入强度,当嵌入的水印信息为 0 时,修改该点的 DCT 系数值,使其等于aver-α;当嵌入的水印信息为 1 时,使其等于 aver+α,嵌入强度α可根据嵌入效果修改。对修改后的 DCT 系数块做 IDCT 变换,再对每个分块按原有顺序进行聚合,即可得到完整的含水印图像。
设原始载体图像为M×M大小,二值水印图像为n×n大小,水印的嵌入过程如下:
(1) 对水印图像进行Arnold置乱变换,改变水印图像的每个像素点的位置,即对水印图像进行加密预处理,得到置乱后的水印矩阵W(i,j),置乱次数t作为密钥保存;
(2)将原始图像I分割为(M/8)×(M/8)个8×8大小互不覆盖的子块 ;同时,也将置乱后的水印图像分割为大小为(n/(M/8))×(n/(M/8))的图像子块;
(3)对分割后的每个图像子块分别进行 DCT 变换,每个 DCT 变换后的图像子块包含64个 DCT 系数;
(4)在DCT变换后的每个图像子块中,选取一个中频系数和在Zig-Zag排序中与其相邻的 6 个系数,设在第K块中选取一个中频系数为yk(i,j),则与其相邻的6个系数就分别为yk(i+3,j-3)、yk(i+2,j-2)、yk(i+1,j-1)、yk(i-1,j+1)、yk(i-2,j+2)、yk(i-3,j+3),计 算 其平均值为:aver= [yk(i+3,j-3)+yk(i+2,j-2)+yk(i+1,j-1)+yk(i-1,j+1)+yk(i-2,j+2)+yk(i-3,j+3)]/6
然后对每一个yk(i,j)作嵌入运算:
yk(i,j)=aver- α,w(u,v)=0,
yk(i,j)=aver+ α,w(u,v)=1
其中:w(u,v)为经过 Arnold 置乱变换后的水印图像;α为嵌入强度,在实际中确定取值,α取值越大,水印的鲁棒性就越强,而水印图像的不可见性就越差,需要平衡考虑不可见性和鲁棒性,选取α=15较为合适。
(5) 将DCT域嵌入水印的每一个子块进行IDCT变换,并将各子块按顺序聚合为一个整体图像I*,即得到含水印的载体新图像。
■3.3 水印提取算法
文中研究的水印算法是一种盲水印算法,即提取数字水印时不需要原始图像。提取水印的算法是嵌入水印的逆算法,对提取水印的图像I*,其提取过程如下:
(1)将含水印图像I*分成8×8 互不覆盖的图像子块;
(2)对每个图像子块分别做 DCT 变换;
(3)找出每个子块中频系数中嵌入水印信息的位置,计算每一个系数yk*(i,j)及与其相邻位置的6个系数的平均值为:Aver*=[yk*(i+3,j-3)+yk*(i+2,j-2)+yk*(i+1,j-1)+yk*(i-1,j+1)+yk*(i-2,j+2)+yk*(i-3,j+3)]/6。
(4)按照下列运算提取水印:
若y*k(i,j)≥ aver*,则 w*(u,v)=1,
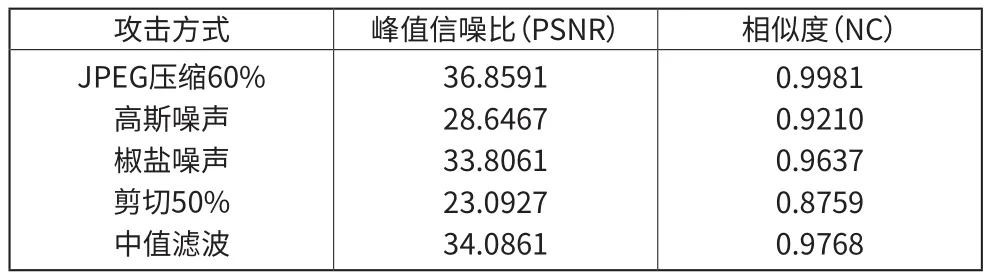
若y*k(i,j) (5)对检测到的水印图像进行逆 Arnold 置乱变换,即可得到提取的水印图像。 仿真实验采用原始载体图像512×512的 fl ower灰度图像,如图3(a), 数字水印为 64×64 “水”文字二值图像,如图3 (b),以MATLAB 7.0为实验平台。水印置乱图像如图4,对嵌入水印的图像不做任何形式的攻击处理,并从中提取出水印信息,如图4(b)所示。从主观视觉的角度看,嵌入水印的图像和原始载体图像几乎没有什么区别,同时,对于提取出的水印图像,用峰值信噪比(PSNR)[6]来对含水印的载体图像评价质量的好坏,根据归一化相关系数(NC)[7]来客观衡量提取的水印与原水印之间的相似程度。PSNR和NC计算公式分别为: 其中:I(x,y)为原始图像、I′(x,y)为嵌入水印后的图像的灰度值;图像的大小为N×N. 单位是分贝(=dB)。 其中:W(u,v)为原始水印图像,W′(u,v)为提取的水印图像。 图3 载体图像和水印图像 图4 水印置乱图像 图5 嵌入水印与提取水印图像 检测算法的有效性,对含水印的图像进行常见的JPEG压缩、椒盐噪声、剪切等抗攻击检测,相应的峰值信噪比PSNR和归一化相关系数NC值,表明了水印的质量,如表1所示。 表1 各种攻击方式的实验结果 从表1可见,在攻击实验中,对于JPEG压缩、高斯噪声、椒盐噪声、滤波攻击实验的NC值都高于0.9。在水印嵌入前,通过对水印图像进行了置乱预处理,使水印信息分解到不同的各个载体块中,因而图像的部分剪切处理对水印信息的提取没有太大影响,提取出来的水印图像与原水印相似度NC为0.8759,鲁棒性较好。各种攻击测试表明,该算法不但具有较好的不可见性,同时也具有较好的鲁棒性。 本文对DCT域的图像水印技术进行了研究,实现了一种盲水印算法方案。在水印嵌入之前,对水印图像进行Arnold置乱加密,增强数字水印系统的安全性。实验表明,算法能够抵御JPEG压缩、噪声攻击等常用的图像攻击,具有较好的不可见性和鲁棒性。 参考文献: * [1]孟倩,王希常,刘江.基于变换的数字水印算法研究[J],微型机与应用, 2010,29(23):37—38 * [2]王静.基于DCT域的图像水印算法研究[D].西北大学,2011 * [3]吴和静,闵昆龙,刘芳等.基于 DCT域的图像数字水印算法及 matlab 实现[J].中国科技信息,2014,09 :129—130 * [4]丁玮,闫伟齐,齐东旭.基于 Arnold 变换的数字图像置乱技术[J].计算机辅助设计与图形学学报,2001,13(4):338—341 * [5]曹军梅.一种基于DCT域的鲁棒性数字水印算法[J].微型电脑应用 .2010,26(1):11—12 * [6]丁玮. 基于离散余弦变换的数字水印图像[J].北方工业大学学报 ,1999,11(3):71—75. * [7]闫丽君,康宝生,岳晓菊.改进的基于DCT的自适应水印算法[J].计算机工程与应用,2011,47(8):197—200.4 仿真实验与分析
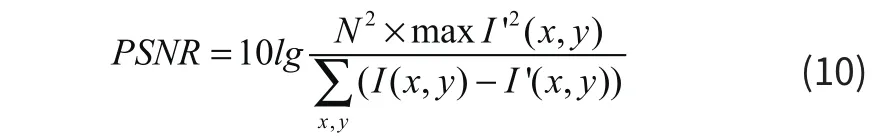
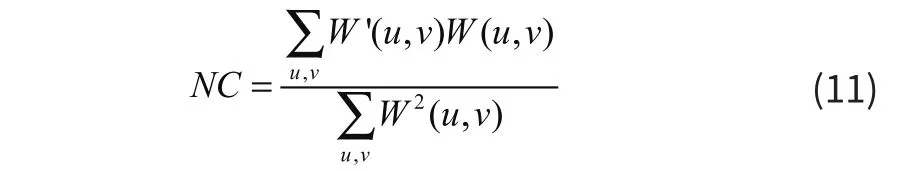



5 结束语
