基于相关性的超声合成孔径成像信号相位校正

王涛，罗林（通信作者），彭朝勇，高晓蓉，叶彩群

（西南交通大学物理科学与技术学院无损检测研究中心，四川成都，610031）

1 相位校正原理

采用超声合成孔径成像技术，通过单发多收方式采集数据。AFMC为全矩阵采集得到的信号，为一个三位数组。其中，每一个矩阵单元都包含了一组A扫数据ATi,Rj(t),即Ti发射，Rj接受的间相关信号。可用AFMC(T,R,t)表示TR接发组A扫信号中t时刻的信号幅值信息。

对成像区域进行离散化处理。设P为聚焦点，晶片Ti发射超声波被点P反射后，被晶片Rj。整个过程的时间为：

其中，已知xi表示Ti和Tj阵元中心点。当tp(x,z)已知，即可得到全矩阵数据矩阵中每个A扫信号在P点的幅值信息。对三维数据矩阵AFMC内所有A扫信号在P点的幅值信息进行叠加，得到全聚焦幅值。

然后我们可以求出待检测区域内每一网格点处的全聚焦超声幅值，再对所得到的值进行成像。

而对参考信号来说，Sn(t)和Sn+1(t)之为两个相邻A扫信号中待计算相关性部分，互相关函数Cn(t)为：

其中T为周期。

在相关校正中，采用互相关函数的离散形式来计算延时参量：

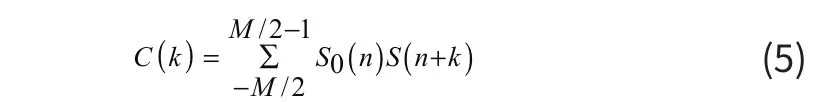
式中S0(n)是标准A扫信号，S(n+k)是相对S0来说的待校正信号,k为采样点序号。M是位于反射点位置两边的采样点数，取20～30为最佳。为了得到延时估计值，需要计算出两列信号互相关函数C(k)最大值。然后，基于邻近互相关系数得到相位误差，平移校正。

为准确找到最大的相关系数Cmax(k0)，即该信号相对参考信号的相位差(时间位置差)Δtj=k0，需要先确定k0的最佳值，为此需要选择最佳相差拾取公式。由此构造函数：

其中C(k)表示相差k步的两相邻信号修正后所得的互相关系数，参数k0是Cmax(k0)取最大值C(k)时的变量。当k=k0时两列相邻信号的互相关系数为C(k)最大值Cmax(k0)。

根据相位差Δtj，所有子孔径中任意i通道的延时差可由下式计算：

其中，当i=0时，τi=0。在实际实验中需要对所有信道只一次进行校正。

因在非均匀情况下，线性部分和非线性部分并存，直接忽略线性部分有可能导致校正后信号之间的互相关系数不如校正保留线性部分的结果。因此将式(7)右边分割成三个部分：

利用如上的三个部分可组合得到三种相差拾取公式：

为寻找最佳的自变量(即最佳相差拾取公式的选择)，构造函数：

其中f(αi)表示消除相位差αi(i=1,2,3…)后得到各信号序列之间的互相关系数。其中α0为使得argmax(f(αi))取得最大值所对应的变量。当αi=α0时各个信号相干叠加效果最强，由此得到最合适的相位校正差量。校正后的信号表示为：

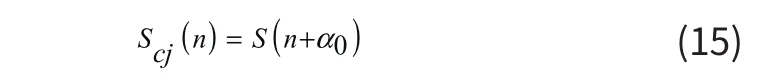
对校正后信号进行(3)式处理得到相位校正超声图像。

2 结果与分析

先对处于同一深度的两个缺陷点进行全聚焦超声成像仿真，并加入随机相位畸变，以随机相位屏模拟波前畸变相位，产生系统的非均匀性噪声。

用滤波函数对一个空间不相关的正态分布随机函数进行滤波，由此得到相位连续分布的非均匀介质相位屏Φ(x)。所构造的滤波函数为满足kolmogonov随机过程的功率谱FΦ(k)。信号的综合延时量ti(i=1,2,3…,N)（其中N为阵元数目）为一组随机序列，可以统计规律受到戒指非均匀性影响的结果。

其中，符合kolmogonov分布的功率谱为：

式r0表示戒指非均匀性，k为波数，R(k)是均值为零、单位方差的Hermitian 复Gaussian随机过程，C为调节常数（可控制相位屏的方差）。该式表示接收信号和相位差之间所满足的统计规律。对所接受的A扫信号加入相应的随机延时。

■ 2.1 仿真

表1是Field Ⅱ的对在同样深度下的两缺陷点进行仿真的结果。

表1 仿真参数

?

图1为仿真两个缺陷点得到的结果，包括无相位差及有相位差的两点成像、相差校正后的两点成像。

图1 两点缺陷仿真结果

为了比较四幅图像，分别计算其横向分辨率，结果如表2所示。

表2 两点仿真图像横向分辨率

由定义已知横向分辨率值越小，横向分辨力越高，经相差校正后的图像横向分辨率值略大于无相差图像的横向分辨率值，明显小于相差校正前的图像横向分辨率值，因此可说明相位校正方法能够提高对于两个缺陷点的横向分辨力，且改进的自适应校正相差方法对图像横向分辨力的提高程度优于自适应校正相差方法。

■2.2 实验

实验设备为Multi2000Pocket多路便携式超声实验系统、奥林巴斯超声探头以及标准试块CSK-IA进行试验。主要参数如表3所示。

设定参数后，先进行全矩阵捕获采集数据，然后对数据进行全聚焦成像处理。因标准试块因其结构特性所造成的相位畸变相对较小,如图2所示。其中图2 (a)是由全矩阵A扫信号离散化结果，图2(b)是单独一列A扫信号。

表3 参数设置

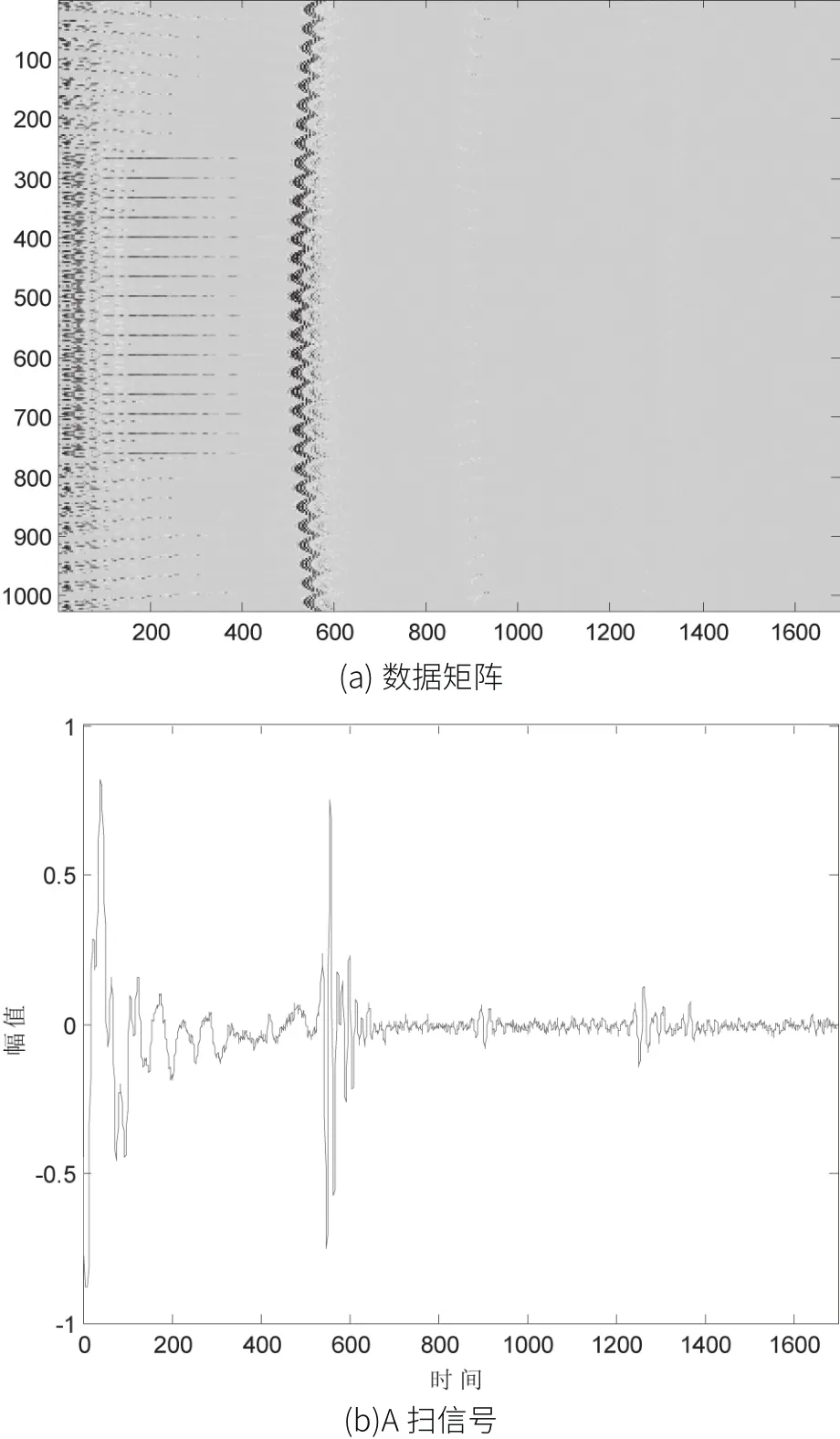
图2 采集的原始信53F7

有无相差的单点全聚焦成像结果如图3(a)和图3(b)。

对加入相位屏后得到的数据进行全聚焦成像，结果如图3(b)和图4 (b)。利用原始自适应校正技术对信号进行处理再全聚焦成像结果如图3(c)和图4(c)所示。而改进后的自适应处理技术对信号优较好的校正，全聚焦成像如图3(d)和图4(d)。

计算其横向分辨率及峰值信噪比来反应两种校正方法的对比。结果如表4、表5所示。

图3 单点成像

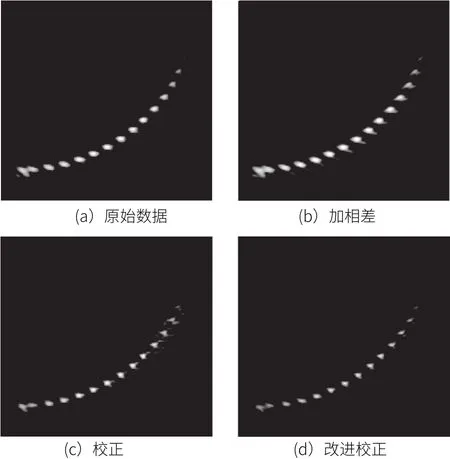
图4 多点成像

表4 横向分辨率

从表4可以看出，不论是单点缺陷还是多点缺陷，两种校正方法对缺陷点的横向分辨率都有所提高，而改进后的校正方法提升程度最高。

表5 峰值信噪比(PSNR)

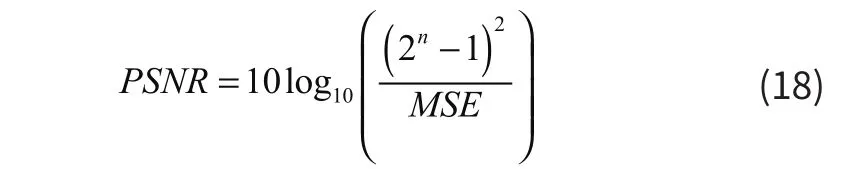
式中n是每个采样值的比特数，MSE是原图像与被处理图像之间的均方误差。

从表5中可以看出，单点和多点缺陷的成像结果表明两种相位校正方法均能提升峰值信噪比，从而改善超声图像提高检测结果，但改进后的校正方法明显优于原始校正。

3 结论

针对超声成技术中，非均匀介质和检测表面不平整造成的原始相位相干校正技术的不足，采用全聚焦技术并结合自适应校正技术，通过计算A扫信号之间的相关性，考虑线性误差、非线性误差及其叠加项对相位校正的影响，优化相位偏差的估计并进行校正。实验结果表明，该方法在仿真模拟和实际实验上，都可以提高相位校正能力，使得图像的横向分辨率、峰值信噪比相对原始技术都有所提高，得到的结果可以有效的反应缺陷的特征信息。

* [1] Holmes C, Drinkwater B W, Wilcox P D. Post—processing of the full matrix of ultrasonic transmit–receive array data for non—destructive evaluation[J]. Ndt & E International, 2005,38(8):701—711.

* [2] Tasinkevych Y, Trots I, Nowicki A, et al. Modified synthetic transmit aperture algorithm for ultrasound imaging[J]. Ultraso nics, 2012, 52(2): 333—342.

* [3]杜英华.合成孔径聚焦超声成像技术研究[D].天津大学,2010.