大规模数据集下基于DBSCAN算法的增量并行化快速聚类
2018-05-03蒋新华廖律超
王 兴 吴 艺 蒋新华 廖律超
1(中南大学信息科学与工程学院 湖南 长沙 410075) 2(福建师范大学数学与信息学院 福建 福州 350108) 3(福建工程学院福建省汽车电子与电驱动技术重点实验室 福建 福州 350108)
0 引 言
聚类分析是数据挖掘的有效手段,已广泛应用于模式识别[1],数据分析[2],图像处理等领域。根据聚类分析的特性,聚类算法分为基于密度的聚类,基于层次的聚类,基于网格的聚类,基于划分的聚类以及基于模型的聚类[3-7]等。
本文主要研究对象为移动对象的轨迹数据,如行人的出行数据,浮动车的移动轨迹等。通过数据分析,发现各类对象潜在的行为模式特征,具有重要意义。考虑到移动对象轨迹数据的非均匀分布特性,采用密度聚类的方法较为合适。传统DBSCAN算法是一种基于密度的聚类算法,因具有较强的抗噪声干扰和发现任意形状聚簇等优点而广受欢迎。然而,随着移动设备的迅猛发展,移动对象的轨迹数据急剧膨胀,面对海量数据处理的需求,传统DBSCAN聚类算法具有较高的复杂度,为了提高聚类质量和聚类的效率,一方面,由于数据的逐步累积特性,可以从增量聚类[8-9]的角度入手,另一方面,可以采用更强大的分布式并行处理架构[10-11],如Hadoop、Spark计算框架。各类方法[12-14]的提出,主要集中解决两个问题:一是数据的分区问题;二是聚类簇的合并问题。文献[15]中的数据分区仅根据街道特定场景划分,聚类簇的合并和增量处理过程,时间复杂度高,计算效率较低。文献[16]给出了一种基于Hadoop框架的方案,但未具体考虑数据的特性对数据进行分区处理,也没给出有效的局部簇合并生成全局簇的方法。
本文针对上述不足,根据实际数据的非均匀分布特性,弹性数据划分,有效过滤噪点数据,提高聚类的质量,设计基于MapReduce分布式批量处理增量数据,合并阶段采用R*-tree索引策略,有效提高了算法的效率,同时根据特定应用,提出基于凸多边形的批量更新增量数据的方法。
1 相关定义和原理
为了更好地描述算法的工作过程,先引入一些相关的定义[15]:
定义1Eps邻域:给定对象p半径Eps内的区域称为该对象的Eps邻域。对象p的Eps邻域内的任意对象q,有:dist(p,q)≤Eps。
定义2核心对象:给定对象p,其Eps领域内的样本点数大于等于MinPts,则称该对象为核心对象,有:|Neps(p)|≥MinPts。
定义3直接密度可达:对象q在对象p的Eps邻域内,且对象p为核心对象,则称对象p到对象q直接密度可达,有:q∈Neps(p)∧|Neps(p)|≥MinPts。
定义4密度可达:对象p0,p1,p2,…,pn,若任意的pi和pi+1满足,pi到pi+1是直接密度可达,则称p0到pn是密度可达。
定义5密度相连:对象o,若存在对象o到p和q都是密度可达,则对象p和q是密度相连的关系。
定义6最小边界矩形(MBR):包含一个簇中所有点的最小矩形。有:
∀p∈A,MBR(A)⟹p⊆MBR(A)
定义7特征点:对于点集A和集合B,如果存在一个点p属于A,使得点P在集合A∪B中是核心对象,那么称点p为特征点,有:
p∈A∧|NA∪Beps(p)|≥MinPts
DBSCAN算法目的在于查找密度相连的最大对象集合,其基本思想是通过遍历集合p中的每个点对象来生成簇。
Hadoop[16]是一个分布式系统基础架构,由于其高可靠性、高拓展性、高效性等,被广泛运用于科研、企业产品的设计中。其中,Hadoop最核心的框架设计是MapReduce模型,它是一个运用于大规模数据集处理的编程模型。在MapReduce中,数据通过采用
2 IP-DBSCAN聚类算法
算法的处理过程主要由五部分组成:数据分区 、本地聚类、获取候选合并簇集、合并判断与处理、重标签,流程图如图1所示。当增量聚类时,获取相邻簇集合阶段,需要读取上一次本地聚类簇的MBRs信息进行一并处理。
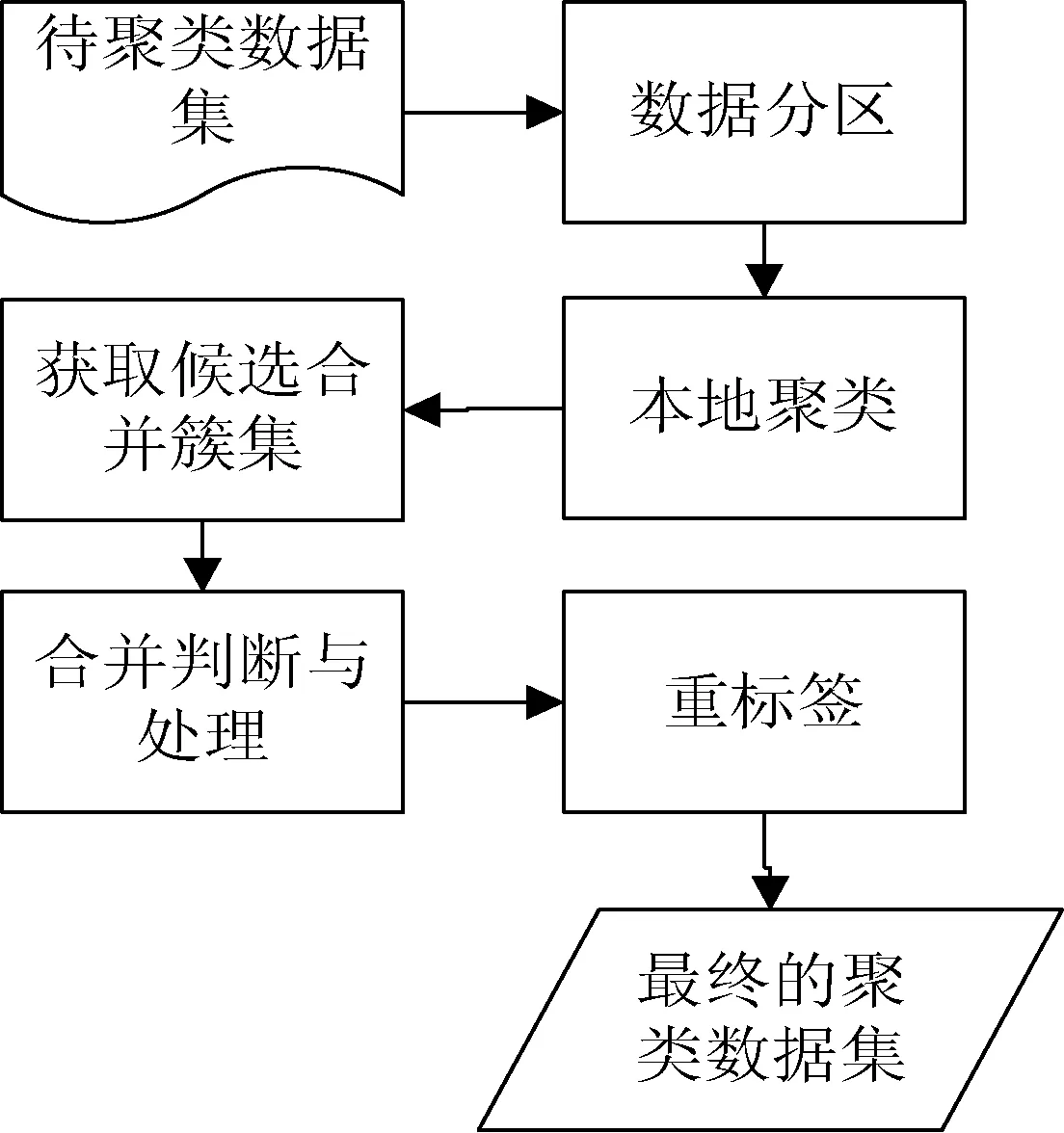
图1 IP-DBSCAN算法框架
2.1 数据分区
针对机器性能相当的Hadoop集群,为平衡计算节点的负载,避免有效数据的丢失,提高算法局部聚类的质量,本文提出了一种基于数据对象数量的弹性数据划分算法。
算法思想:采用二叉索引树生成网格空间,索引的每个结点记录一个MBR和网格中包含点的个数cnt,根节点存放给定的初始网格大小和点集个数。
算法自顶向下,逐层采用二分法分割网格,直到当前网格的长宽均不大于指定长度m时停止,通过建立MapReduce作业统计每个网格中点的个数,遍历每个二叉索引树的结点,若结点中的cnt值小于等于指定参数maxCnt时,将此结点加入分区集合list中。由于实际数据的非均衡分布,需要对分区集合list进行均衡划分处理,先将分区集合list按cnt值从小到大排序,再结合贪心算法对分区集合list进行重组,最终得到n组样本点数相近的分区。
其中,上述各参数初始化如下:m取2×Eps,n取Reduce个数,maxCnt取(点集个数/n)。算法伪代码如下:
算法1数据划分算法
输入:数据集D,数据集的网格区域S,DBSCAN参数Eps,网格最大的点个数cnt
输出:分区网格集合G
1: create binary tree index IndexTree;
//创建二叉索引树
2: IndexTree.root.grid ← S;
3: splitByRecursive(Index.root, Eps) ;
//递归进行二分划分
4: Map:
5: for all point pt in P do
6: for all grid in IndexTree do
7: if pt is in grid then
8: gird.count++;
9: Reduce:
10: for all grid in IndexTree do
11: sum total points count for grid;
//统计格子中点的个数
12: create a set G;
13: grid ← IndexTree.root;
14: getPartitionByRecursive(grid, cnt, G);
//递归获取分区集
15: return G;
第3行使用递归函数,对满足条件的网格进行对半划分。
第14行,调用递归函数来获取满足条件的分区集合。在此函数内,首先判断当前网格内的点个数是否小于cnt,若满足,则加入到G中,否则进行左右子树递归调用。分区算法示意图如图2所示。
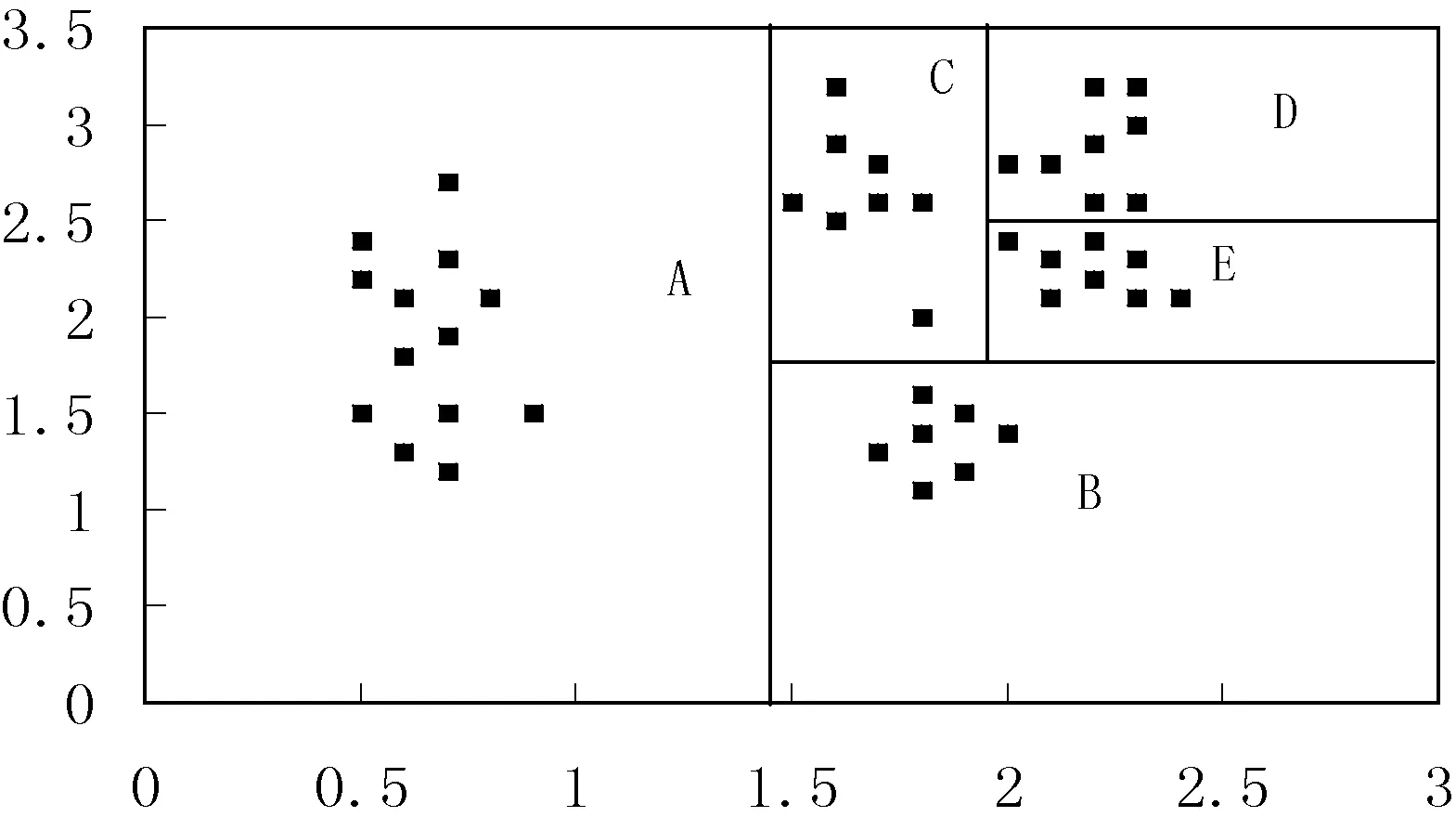
图2 分区例图
图2中,点集个数为44,Hadoop集群中DataNode个数为3,则maxCnt取值为15,可得图2中ABCDE五个分区的集合。根据区域中cnt值排序可得:BEDCA,利用贪心算法进行重组得到最终的3组分区:(A),(B,C),(D,E),数据量越大,此分区算法效果越明显。
2.2 本地聚类
数据划分完成后,新建一个MapReduce作业执行本地聚类,在Map阶段,以分区ID作为输出的key进行数据分发,使相同分区的数据分发在同一计算结点进行聚类。算法描述如下:
算法2本地聚类算法的Map函数
输入:
key:NULL;Value:包含经纬度信息的点pt
输出:
Key:点pt所属的分区ID ; Value:点pt的经纬度信息
1: for all mbr in MBRS do
2: if pt in mbr then
3: Emit(mbr.getPartitionId(), pt);//数据写入HDFS
在Reduce阶段进行本地聚类,得到聚类结果后,计算最小边界矩形(MBR),为方便下一阶段的执行,将此MBR范围拉伸Eps大小,并存储于HDFS系统中。算法如下:
算法3本地聚类算法的Reduce函数
输入:Key:分区ID:partitionId; Value:点集P={p1,p2,…,pn}
输出:Key:点pt所属的分区ID;Value:点pt的经纬度信息
1: Do clustering the all points by using the DBSCAN algorithm;
2: clusters ← getClusterResult();
//读取聚类得到的簇集合
3: for all cluster in clusters do
4: mbr ← getPointsMBR(cluster);
5: Emit(partitionId, mbr);
//将每个簇的MBR信息写入HDFS
6: for all pt int P do
7: Emit(partitionId, pt);
//将聚类后的点信息写入HDFS
2.3 获取候选合并簇集
本阶段通过判断不同簇所属MBR之间的邻接关系,得到候选合并簇集。首先,将原MBR扩大Eps个单位,再判断任意两个扩大后的MBR是否有交叉,若交叉,则该两个MBR所在的簇为候选合并簇。如图3所示,若本地聚类生成4个簇A、B、C、D,通过扩大MBR可得图4,可以得到A和B、A和C、B和C均为候选合并簇。
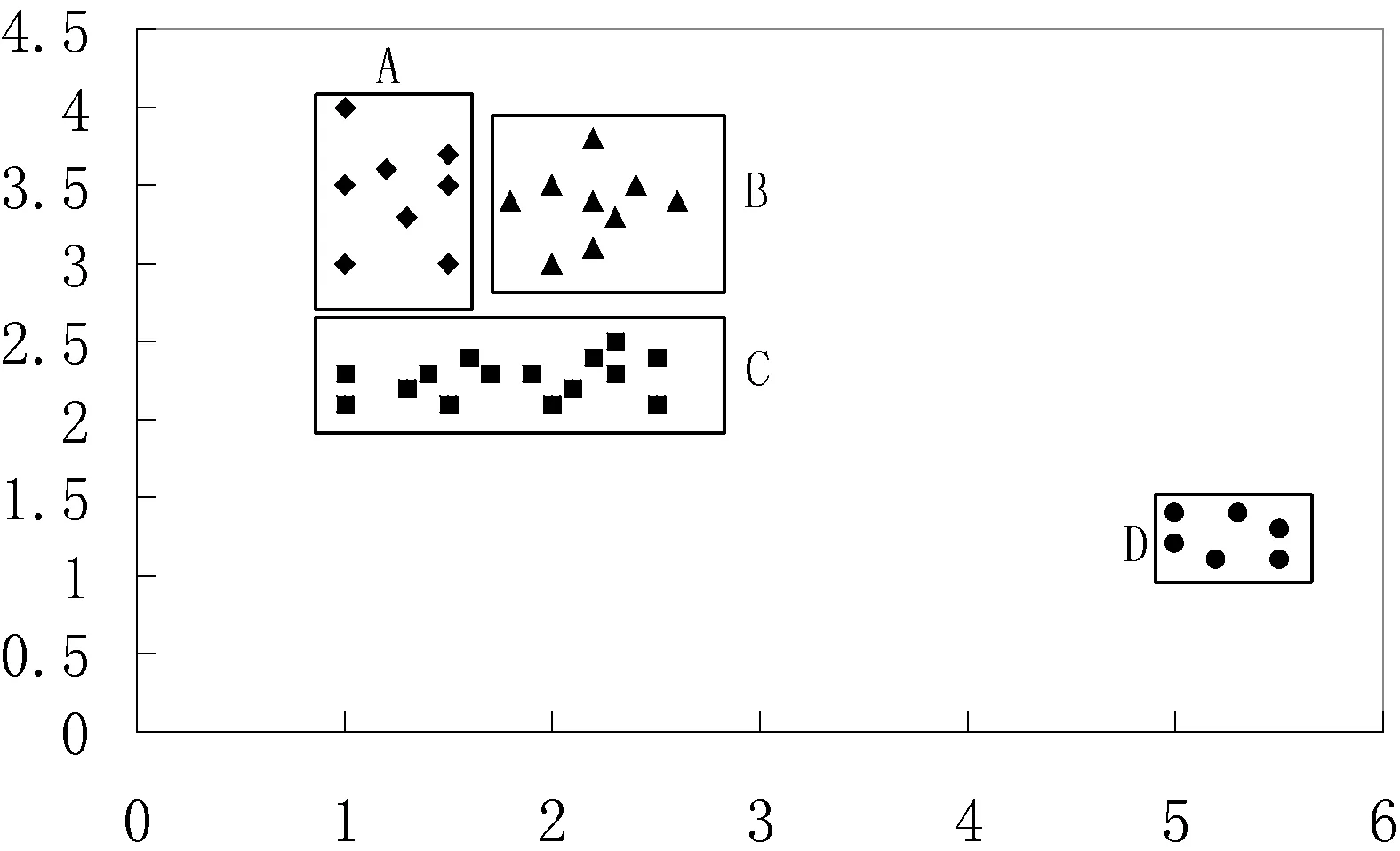
图3 簇合并例图(Eps=0.5,minPts=2)
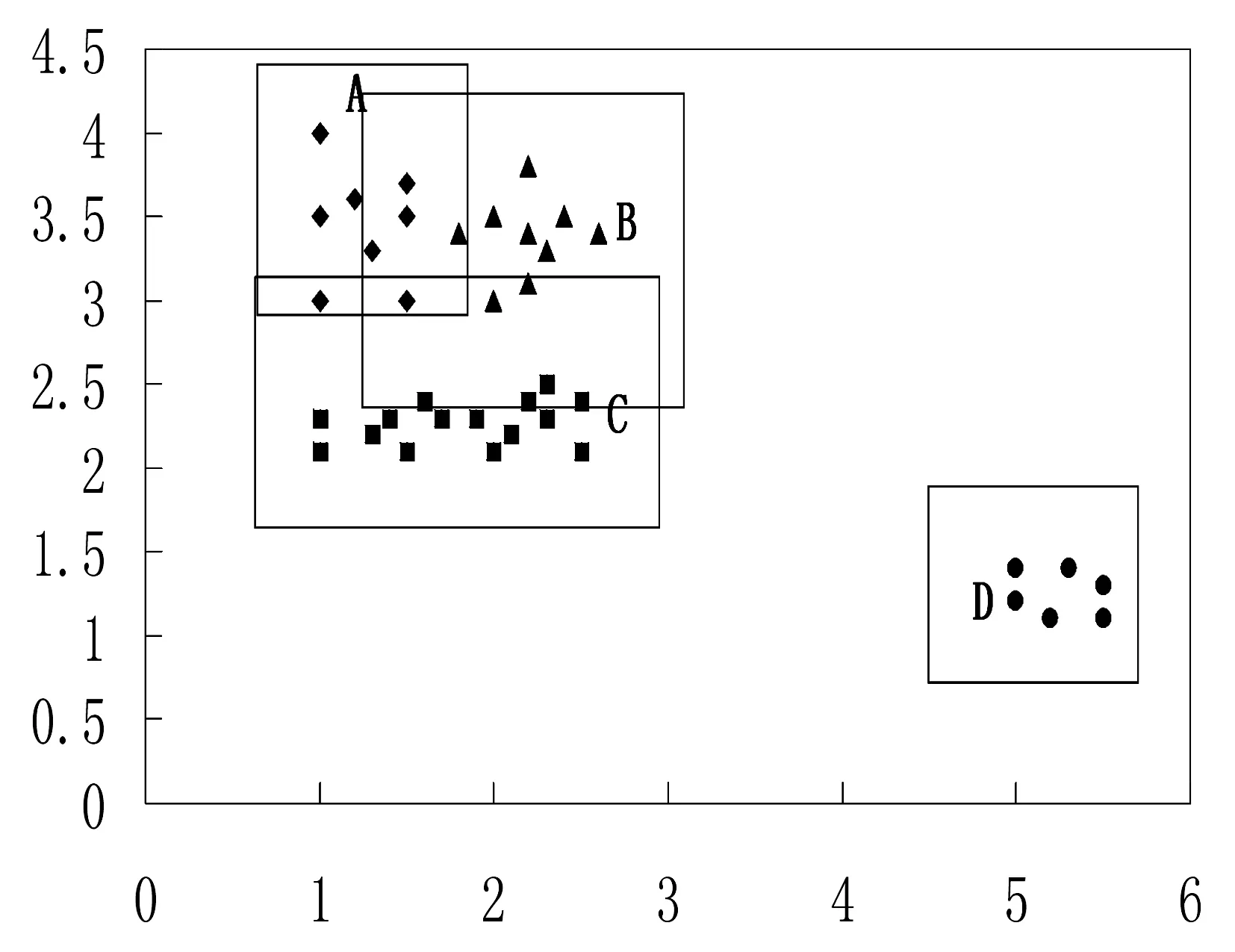
图4 簇合并例图(Eps=1.5, minPts=2)
算法4获取合并簇候选集函数
输入: MBRS
输出: mergePairs< mbri,mbrj>
1: for all mbr in MBRS do
2: mbrs ← findAdjacentMBR(mbr);
//根据相邻规则得到相邻MBR集
3: return mergePairs;
在算法中,mergePairs候选集合中的mbr组表示为:<(pIndexi, cIndexi),(pIndexj, cIndexj)>,pIndex表示分区的索引号,cIndex表示聚类簇的索引号。
2.4 合并判断与处理
本阶段通过建立MapReduce作业来实现并行化处理,提高算法执行效率,分为合并判断与合并两个过程。
2.4.1 候选簇合并判断
合并判断过程:在Map阶段,对候选合并簇所包含数据点的进行分发,过程描述如下:
算法5合并判断过程Map函数
输入:mbrs:聚类数据中所有簇的MBR信息集; Key:NULL;Value:pt点信息
输出:Key:parId1,cId1;parId2,cId2,其中parId为分区ID,cId为簇ID,Value:pt点信息
1: mbrs ← getTheMBRS();
2: id ← pt.partitionId + ", " + pt.cId;
//读取点pt的分区信息
3: ids ← findMergeCandidates(mbrs , id);
//获取点pt所在MBR的合并对信息
4: for all mergeId in ids do
5: Emit(id+ ”;” +ids , pt);
//将相应信息写入到HDFS
在Reduce阶段,建立两个簇所属的R*-tree索引结构以加快后续的查询效率,记为R1,R2,则有R3=R1+R2,依次判断R1中每个点对象在R2和R3的Eps邻域内包含点个数的关系可得特征点集合。对于候选合并簇A和B,若满足:∃p,p∈A且|NA∪Beps(p)|≥MinPts,∃q,q∈A且|NA∪Beps(q)|≥MinPts,q∈Neps(p),则簇A与簇B可合并。
证明:对于点集D与D′中的两个候选合并簇A和B,有A={o|o≻Dp′},B={o|o≻D′q′},若∃p,p∈A且|NA∪Beps(p)|≥MinPts,且存在至少一个q∈B,q∈NA∪Beps(p),则对新簇A′={o|o≻D∪D′p},有{q}⊆{o|o≻D∪D′p}。若|NA∪Beps(q)|≥MinPts,则有B={o|o≻D∪D′q},即簇B也是一个关于点p的密度相连点集,从而有B⊆{o|o≻D∪D′p},即所有关于点p密度相连的点均在关于点q密度相连的点集当中,因此簇A与簇B可合并,下面以图5为例进行说明。
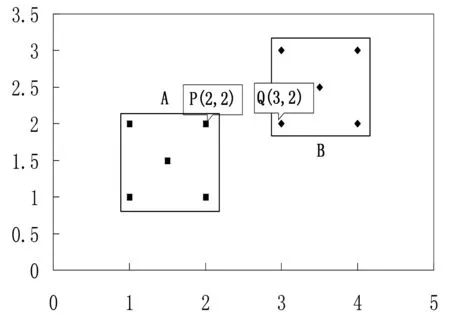
图5 判断簇合并例图(Eps=1, minPts =3)
集合A中,P为边界点,集合B中,Q为边界点,在集合A∪B中,P和Q均为核心点(Eps范围内点个数大于3),且P到Q为直接密度可达,Q的Eps领域内的点均与点P密度相连,因此,集合A可扩展簇范围到B,即集合A和集合B可合并成一个簇。
综上,合并判断算法只需要对每个特征点,判断其Eps范围内是否包含另一个簇的核心点。
算法6合并判断过程Reduce函数
输入:Key: partitionId1; cId1; partitionId2; cId2 ; Value: 点集合P
输出:Key: partitionId1; cId1; partitionId2; cId2 ;
Value: true/false: 表示两个簇是否可以合并
1: pts1 ← getAllPointsBelongTo(partitionId1 , cId1);
//读取属于簇1的点集
2: pts2 ← getAllPointsBelongTo(partitionId2 , cId2);
//读取属于簇2的点集
3: rtree ← usePts1ToBulidRTree;
//创建R树
4: add pts2 to rtree;
5: for all pt in pts1 do
6: neighborPts ← rtree.search(pt , Eps);
//查询点p的Eps领域内点集
7: if neighborPts.size() > minPts then
8: if hasOtherCorePoint(neighborPts, pt)
9: Emit(key, true);
10: return;
11: Emit(key, false);
在第8行判断点pt的Eps范围内点集是否包含其它簇的核心点,若包含,返回true,否则返回false。通过R*-tree索引结构的使用,可以有效提升算法的执行效率。
2.4.2 候选簇合并
通过候选合并簇的判断处理,最终得到可合并的候选簇集。为解决多个簇分配同一标签问题,以(pIndex, cIndex)为结点信息建立无向无环图,图中的边表示相连的两结点对应的簇可合并,在分配全局ID时,通过深度优先搜索算法获取具有同一全局ID的簇的集合,并更新簇所属的MBR范围。算法如下:
算法7基于合并簇的图模型建立和查询
输入:mergePairs(包含了所有可合并的簇对),其元素格式为:
输出:globalIDs
1: g ← createTheDAG()
//创建无向无环图
2: for all pair in mergePairs do
3: g.insert(pair.ID1, pair2);
4: globalId ← 0;
//记录全局ID
5: globalIDs ← createEmptyList();
//创建空列表
6: keys ← g.getKeySet();
//获取无向无环图的所有结点信息
7: fo all key in keys do
8: ids ← g.DFS(key);//采用深度优先搜索获取与
//key连通的点
9: if ids.size() == 0 then
10: continue;
11: globalId++;
12: for all id in ids do
13: if not globalIDs.contain(key+”,”+id) then
14: globalIDs.add(key +”,”+id, globalId);
15: return globalIDs;
2.5 重标签
本阶段通过建立MR作业来实现数据的重标签。在Map阶段,通过读取点所在的簇信息,结合上述阶段所得到的合并簇的无向无环图,为其分配唯一的全局簇ID。
2.6 增量学习
根据不同的应用场景,本文提供两种增量学习方法。
方案一:侧重聚类精度,充分考虑每个点对聚类结果的影响,具体做法如下:当新增数据集时,做如下两点处理:1) 读取上一次聚类的噪点数据叠加新数据集一并进行增量学习;2) 在2.3节读取历史聚类所得的MBR信息集,得到新的簇和历史聚类所得簇的候选合并集,后续处理步骤不变,算法名称简记为IP-SBSCAN(Incremental parallelization-DBSCAN)。
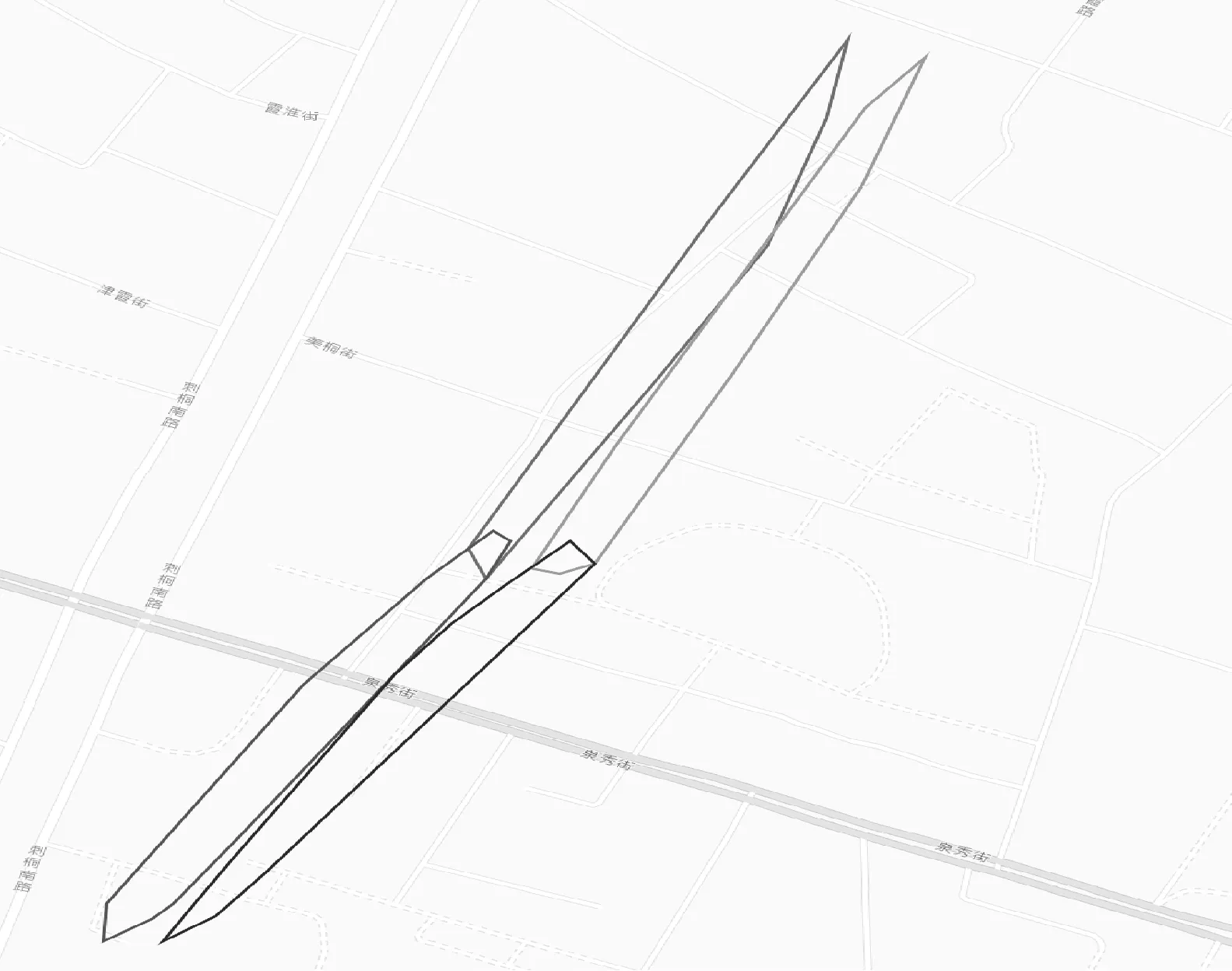
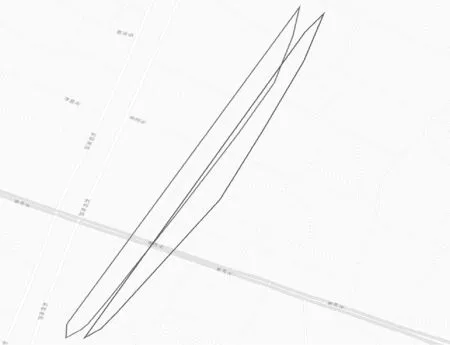
方案二:对聚类的精度要求不太高,侧重聚类的整体效果,如交通新道路发现等。算法思想:在2.4节处理后根据可合并的簇利用Graham扫描法对簇中的点集构建一个凸的最小覆盖多边形用于表示簇的结构信息,整个算法时间复杂度为O(nlogn)。用于表示簇结构的顶点个数K,满足K< 为了验证本文方法的性能,进行模拟实验,实验软件平台为Eclipse,Java语言,Hadoop2.6版本,ubuntu操作系统。硬件设备Master主机1台Slaver机3台,配置为CPUi5-3470,内存4 GB。 实验数据集[17]采用福建省福州市的浮动车轨迹数据作为算法实验测试数据集, 数据主要包括车辆ID、经纬度、速度、方向及车辆类型等字段信息。整个数据集由2014年5月的浮动车轨迹数据组成,数据集覆盖地理空间的经度范围为[119.113,119.684],纬度范围为[25.904,26.155],区域面积约为1 430 km2。 为了验证本文方法的性能,实现了传统单机DBSCAN算法,文献[15]中方法,MR-IDBSCAN算法(文献[16]),IP-DBSCAN算法(本文方法),IP*-DBSCAN算法(本文方法),从聚类数量、噪点数、运行时间等维度进行对比实验,实验结果如表1所示。 表1 福建省福州市浮动车部分数据 图6、图7和图8分别给出了时间效率、聚类数和噪点数对比情况。 图6 算法时间效率对比图 图7 聚类后簇个数对比图 图8 聚类后噪点个数对比图 实验结果分析: (1) 聚类数量 由于弹性分区算法的引入,本文IP-DBSCAN算法在并行化处理时,能够有效减少噪点数据,局部聚类更完全,聚类效果明显优于文献[16]MR-IDBSCAN算法。同时,IP-DBSCAN算法聚类效果十分接近单机DBSCAN聚类效果,增量处理方法效果佳,文献[15]根据街区进行数据分区,与实验样本数据(交通浮动车数据)特点有一定的吻合,也取得了较好的聚类效果。 (2) 噪点个数 增量并行化方法处理过程中,需要分发数据,数据的合理划分对聚类的效果影响较大,三种并行化增量方法的聚类噪点数均没有传统DBSCAN算法一次聚类效果好,噪点数较多。而IP-DBSACN算法在弹性数据分区过程能有效减少噪点,同时在增量数据学习时,读取原始噪点数据追加学习,充分处理噪点数据,通过实验对比可知,本文方法聚类噪点数量远少于另两种增量并行化方法。 (3) 聚类时间 随着数据量逐步增大,DBSCAN算法耗时大幅上升,IP-DBSCAN则体现出Hadoop并行计算的优点,新的基于R*-tree的合并算法,使IP-DBSCAN在数据量增大时聚类速度快于MR-IDBSCAN,效果突出。 另外,在增量学习方案中,本文给出的另一种基于凸多边形的IP*-DBSCAN方法。理论上分析,该方法只注重簇的结构形态,处理稍显粗糙,聚类质量比IP-DBSCAN方法低;合并阶段,由于其不需逐个处理增量数据点,时间效率要比IP-DBSCAN方法高。为了体现局部聚类簇的精细程度和更好的展示效果,增量对比实验采用了课题组前期工作[17]对数据集进行有向处理,同一主干道路上方向不同的浮动车轨迹点可以聚类识别,实验效果如图9-图13所示。实验结果与理论分析基本吻合,随着数据量的增大,两者的聚类效果差距逐步减小,而IP*-DBSCAN在运行效率上具有一定优势。 图9 基于有向的局部聚类效果图 图10 基于IP*-DBSCAN的增量学习1 图11 基于IP*-DBSCAN的增量学习2 图12 基于IP*-DBSCAN的增量学习3 图13 基于IP-DBSCAN的增量学习 本文针对传统DBCAN算法的实际应用需求,面对海量数据处理时的不足,提出了基于Hadoop分布式计算框架的并行增量聚类解决方案,重点进行数据分区的弹性处理和聚类簇的判断与合并处理,给出了两种增量数据集学习方法。通过对比实验表明,方法具有较好的聚类效果,同时聚类的时间效率较高,能实现大规模数据的在线处理。下一步工作将进行更大数据规模的集群测试,优化算法的参数,同时针对不同应用场景数据的特点,进一步改进优化算法。 [1] 蒋鸿玲,张楠,李克,等.基于MapReduce的出租车停泊点智能推荐算法[J].计算机应用与软件,2016,33(2):254-258. [2] Wang W T,Wu Y L,Tang C Y,et al.Adaptive density-based spatial clustering of applications with noise (DBSCAN) according to data[C]//Proceedings of the 2015 International Conference on Machine Learning and Cybernetics.Piscataway:IEEE,2015,1:445-451. [3] Carvalho A X Y,Albuquerque P H M,De Almeida Junior G R,et al.Spatial Hierarchical clustering[J].Revista Brasileira de Biometria,2009,27(3):411-442. [4] Pilevar A H,Sukumar M.GCHL:A grid-clustering algorithm for high-dimensional very large spatial data bases[J].Pattern recognition letters,2005,26(7):999-1010. [5] Tvrdík J,Krivy I.Differential evolution with competing strategies applied to partitional clustering[M]//Swarm and Evolutionary Computation.Springer Berlin Heidelberg,2012:136-144. [6] Sander J,Ester M,Kriegel H P,et al.Density-based clustering in spatial databases:The algorithm gdbscan and its applications[J].Data mining and knowledge discovery,1998,2(2):169-194. [7] Fraley C,Raftery A E.Model-based clustering,discriminant analysis,and density estimation[J].Journal of the American Statistical Association,2002,97(458):611-631. [8] 孟海东,任敬佩.基于云计算平台的动态增量密度算法研究[J].计算机应用与软件,2016,33(6):16-19. [9] Chakraborty S,Nagwani N K.Analysis and Study of Incremental DBSCAN Clustering Algorithm[J].Eprint Arxiv,2014,1(2):2011. [10] 赖丽萍,聂瑞华,汪疆平,等.基于Map Reduce的改进DBSCAN算法[J].计算机科学,2015,42(11A):396-399. [11] Xu Zhengqiao,Zhao Dewei.Research on Clustering Algorithm for Massive Data Based on Hadoop Platform[C]//International Conference on Computer Science and Service System.IEEE Computer Society,2012:43-45. [12] 王卓,陈群,李战怀,等.基于增量式分区策略的Map Reduce数据均衡方法[J].计算机学报,2016,39(1):19-35. [13] 荀亚玲,张继福,秦啸.Map Reduce集群环境下的数据放置策略[J].软件学报,2015,26( 8):2056-2073. [14] Fu X,Wang Y,Ge Y,et al.Research and Application of DBSCAN Algorithm Based on Hadoop Platform[M]//Pervasive Computing and the Networked World.Springer International Publishing,2014:73-87. [15] Silva T L C D,Neto A C A,Magalhães R P,et al.Towards an Efficient and Distributed DBSCAN Algorithm Using MapReduce[C]//International Conference on Enterprise Information Systems.Springer,Cham,2014:75-90. [16] Noticewala M,Vaghela D.MR-IDBSCAN:Efficient Parallel Incremental DBSCAN algorithm using MapReduce[J].International Journal of Computer Applications,2014,93(4):13-18. [17] 廖律超,蒋新华,邹复民,等.浮动车轨迹数据聚类的有向密度方法[J].地球信息科学学报,2015,17(10):1152-1161.3 实验与结果分析
3.1 实验环境
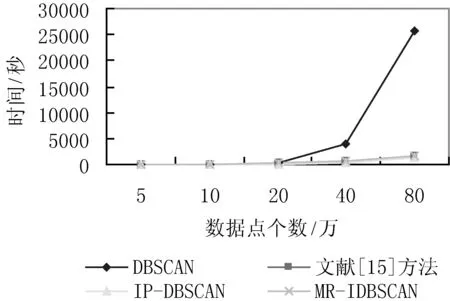
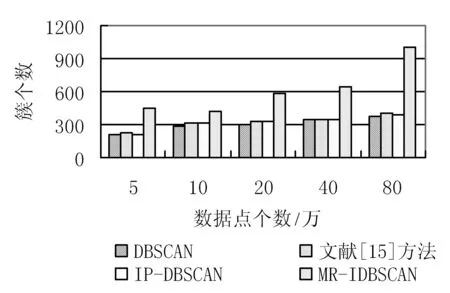
3.2 实验结果与分析




4 结 语
