元胞自动机压缩算法仿真卫星云图
2018-05-03张昭晖梁立为
邹 阳 王 将 张昭晖 刘 祎 梁立为
(昆明市气象局 云南 昆明 650000)
0 引 言
卫星云图在采集、处理、传输和存储过程中,由于数据量较大,云图数据的压缩方法研究非常重要。传统的方法有Huffman编码、预测编码、变换编码(包括离散余弦变换、小波变换等)、分形压缩[1-9]等,都存在多种冗余、编码效率不高和压缩比较低等问题。
元胞自动机[10]是一种离散的时空动力系统,每个单元的状态受其领域的状态影响,同时也影响着领域的状态。元胞局部之间相互作用,其状态通过一定的相似规则的转换作同步更新。
可逆元胞自动机[11]的转换规则是单射且漫射的,可以重建。加权有限自动机[12]可以定义一个多分辨率图像,有限自动机的每一个状态对应整幅图像的某个子图像,也叫状态图像。转换矩阵一般用其状态图像的线性组合表示,即用有限自动机来近似表示。
本文针对云图资料的特征和天气预报中的实际应用情况(无需十分精确),设计可逆细胞自动机和加权有限自动机的灰度图像数据有损压缩算法。通过实验验证尝试得到较好压缩效果。
1 方块编码和可逆元胞自动机算法
1.1 编码思想
方块编码算法是把原图分割成若干个n×n像素的子方块。因为云图子方块内的像素具有很高的相似特征,分配某个适当的比特数表示该子方块内各个像素的灰度值。
根据卫星云图局部范围内有较高的相似特性,以及云图传输、存档和使用具体实际要求,简化方块编码和可逆元胞自动机算法。仅对子方块的平均灰度值进行量化并编码传输,接收端译码后逆量化得到子方块的平均灰度值,以此作为子方块内各个像素的灰度值。在卫星云图数据能较好地保留图像信息的基础上,使压缩比数倍提高和压缩时间大大缩短。
在此基础上,对子方块更进一步采用能较好保持图像细节的元胞自动机的编码算法,特别是对非均匀子方块更加能达到保留原图信息的效果。可逆元胞自动机实现方法有分区元胞自动机(partitioned CA)、二阶元胞自动机(second-order CA)、Margolous元胞(Margolous CA)等[13]。本文采用方块编码解决子方块局部平均灰度值的级别编码,参照Margolous元胞的二值图编码方法标志子方块结构特性,即子方块像素取值为布尔值(0表示比子方块局部平均灰度值更白一级,1表示比子方块局部平均灰度值更黑一级)。
1.2 算法实现
对一幅云图数据进行划分的方法是以光栅扫描方式从左到右、从上到下以此扫面成2×2的像素块,即为子方块,实际上也是Margolous元胞的一个2×2元胞块,可以将其看做一个有4个分量的可逆元胞。每个编码分两部分,均值编码和分类编码,是对每一图像子方块,依据一定法则,判断其类型。
1.2.1 均值编码
均值编码根据子方块平均灰度值大小分为16个区间,在编码之前对云图数据进行预处理,主要是滤掉云的信息以外的部分,包含地域、积雪等固定灰度值信息。这些云以外的固定信息的灰度值通常不同于云的灰度值,便于提取,确定为云信息的临界灰度值,小于临界灰度值的标志为0(黑色),大于临界灰度值的重新分类。如表1所示,用十六进制数将16种状态进行了标志。
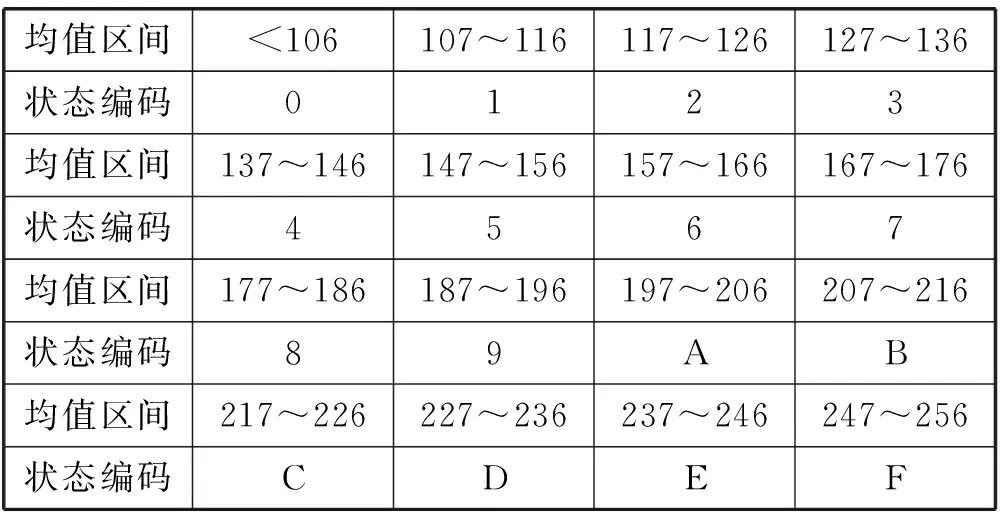
表1 均值编码状态集
元胞自动机由元胞空间、元胞、邻域及规则四部分组成,即CCA=(Ld,S,N,f)[14]。
式中:
1) 元胞状态S为0或1。
2) 元胞邻域N为2×2元胞块。
3) 转换函数f:S2→S2。
4) 逆转换函数f-1:S2→S2。
1.2.2 分类编码
Margolous元胞含有4个分量的元胞。分类编码判断每个元胞(子方块)分量与该元胞平均灰度值大小差值。通过大量云图数据实验,计算峰值信噪比(PSNR)与临界差值关系曲线,选取与PSNR最大值对应的临界差值(这里临界差值为-10)。差值大于-10状态标志为1,否则为0。Margolous元胞可能的状态为16个。如图1所示,用十六进制数将16种状态进行了标志。
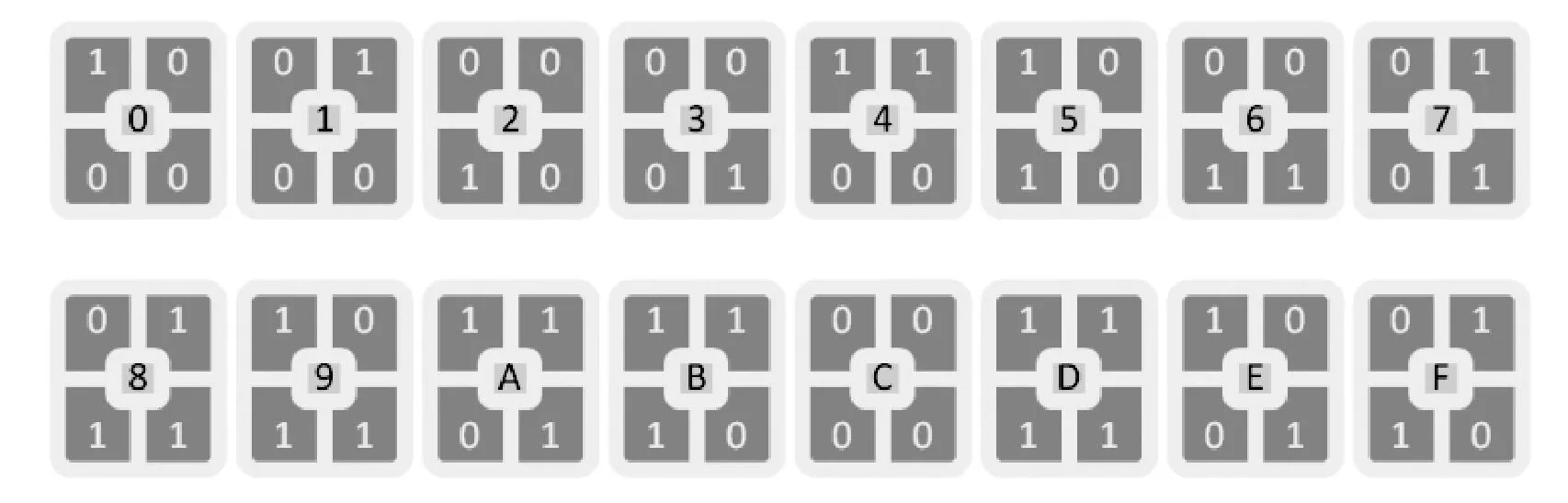
图1 四子元胞自动机的状态集
元胞自动机有如下特点:
1)元胞状态S如图1所示。
2)元胞邻域N为2×2元胞块。
3)转换函数f:S4→S4。
4)逆转换函数f-1:S4→S4。
转化函数即是转换规则,可以看作一个排列,是一一映射。例如f(B)→(1,1,1,0)。解压时同样可以唯一地恢复原多级灰度像素图像素序列。
每个子方块也是一个单位元胞,编码有两位,都是十六进制的,前位是2×2元胞块(4个像素)的均值编码,标志子方块整体特性,后位是分类编码,描述子方块局部细节。编码过程简单又不失细节,可以得到与原图像十分相似的重建图像。
2 方块编码和有限加权元胞自动机算法
2.1 编码思想
整个图像数据分为2×2子方块(4个元胞像素)。用有限自动机的一个状态表示整幅图像数据,主要对子方块的平均灰度值进行量化并编码,对某个状态的每个子方块的元胞进行处理,用已有的状态(包括这个子方块的状态图像)的线性组合来近似表示这个元胞像素状态。参考有关文献[15-16],简化这种线性组合的权重系数,通过对整个像素图数据的子方块结构的统计,选择有代表性的分类结构作为权重系数。同样既能较好地保留图像信息,又使压缩比数倍提高和压缩时间大大缩小。
2.2 算法流程
本文提出的算法流程如图2所示。
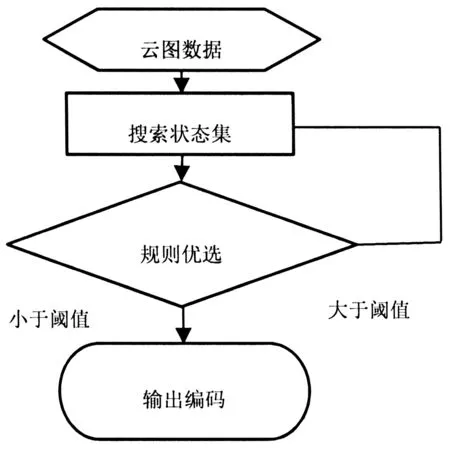
图2 方块编码和加权有限元胞自动机算法流程图
具体步骤如下:
步骤1输入卫星云图数据,进行预处理,即分块处理,块与块之间没有重叠,初始化群体,生成CA个体。
步骤2对CA个体进行统计分析,根据卫星云图有邻域范围内有高度的相似性,归类具有较好代表性的特征块作为状态集。
步骤3根据转换矩阵进行CA变换,通过调整方块单元总的灰度差值,将灰度差值按照转移矩阵的系数(权值)分配到2×2元胞块(4个像素)。用峰值信噪比(PSNR)作为误差阈值与原图进行比较。如果小于阈值则输出编码,否则调整灰度差值再次进行元胞自动机变换,直至小于阈值或者达到最大迭代次数,输出编码。
2.3 算法实现
同样对一幅云图数据分成2×2的像素块,即为子方块,实际上也是分割成元胞块的四个象限,可以将多分辨率图像用加权有限元胞自动机表示。每个编码分两部分,均值编码和加权编码,是对每一图像数据子方块,依据一定法则,判断其转移矩阵类型(转移矩阵的系数表示权值)。
2.3.1 均值编码
均值编码根据子方块平均灰度值大小分为16个区间,在编码之前对云图数据进行预处理同上。如表1所示,用十六进制数将16种状态进行了标志。
2.3.2 加权编码
下面给出表示多分辨率图像数据的加权有限元胞自动机[15-16]的定义。最初加权有限元胞自动机是一个三元组(Q,N,C),其中Q是理论上子方块各个元胞邻域所有状态集合,设7层权重级,表示子方块4个元胞邻域,共计6 666种标志。我们对多个512×512分辨率的云图数据个例进行统计,发现Q基本上在360种以下,而子方块数量达到65 536,可见卫星云图数据子方块具有极高的相似性。通过对卫星云图的子方块结构的统计,选取有代表性、能刻画云图细节纹理的(主要是云团边缘部分)若干组状态集合,这种集合一般不大于64种,所占比例达到97.2%。此时加权有限元胞自动机是(S,N,C),S∈Q:
1) 元胞状态S为代表性的元胞邻域状态集合。
2) 元胞邻域N为2×2元胞块。
3) 转换矩阵{C|Ci∈S∈Q,i≤64}。
加权编码判断每个元胞(子方块)分量与该元胞平均灰度值大小差值,权值有-1、-2/3、-1/3、0、1/3、2/3和1。选取元胞有代表性的状态集合为64个。如图3所示,用两位十六进制数将64种状态进行了标志。
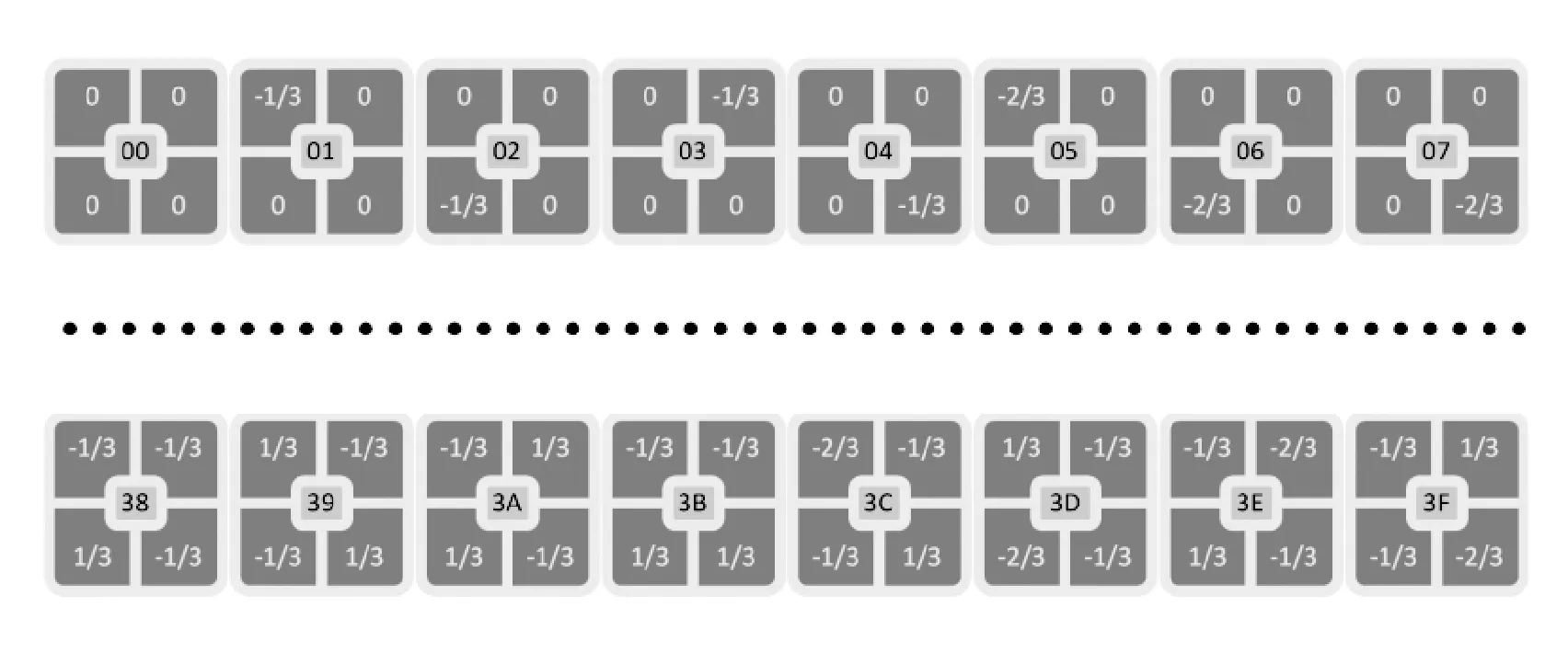
图3 加权有限元胞自动机的状态集
转化矩阵即是转换规则,可以看做一个排列,是一一映射。例如:
f(3B)→(-1/3,1/3,-1/3,1/3)
解压时同样可以唯一地恢复原多级灰度像素图像素序列。每个子方块也是一个单位元胞,编码有三位,都是十六进制的,前一位是2×2元胞块(4个像素)的均值编码,标志子方块整体特性,后两位是加权编码,描述子方块局部细节。基于云图结构信息的编码过程简洁实用,重建图像与原图像比较相似。
3 仿真效果及分析
采用FY2E红外图像作为测试对象,图像数据是512×512,8 bpp像素的灰度云图,数据格式为二进制,大小为262 144 bit,256级灰度值,十进制数据文件大小为1 035 264 bit。
以压缩比、峰值信噪比(PSNR)和均方差(RMS)为指标,检验仿真实验效果。
实验环境,PC 2.0 GHz;内存4 GB;Windows 7.0;借助MATLAB仿真平台对本文算法进行实验。
3.1 方块编码和多子带元胞自动机变换仿真
采用2013年10月7日9时0分FY2E红外图像作为测试对象。
通过变换实验,可见该方法在保持云图细节部分和重建质量基本不变的情况下,提高了压缩比,达到了较好的效果(见图4)。重建图像信噪比下降主要是对子方块类型的粗量化引起的,可以经平滑处理后在主观视觉上并无明显区别。

图4 2013年10月7日9时0分FY2E红外图像实验结果对比
3.2 方块编码和有限加权元胞自动机仿真
测试2013年10月9日11时0分FY2E红外图像。实验结果显示该方法搜索云图细节结构,保证云图质量,减小云图数据中的冗余信息,虽有一些细小失真,但可以接受,总体效果较好。针对云图特点进行有效压缩,在可接受的有损范围内获得较好的压缩比。重建的云图直观效果明显(见图5)。

图5 2013年10月9日11时0分FY2E红外图像实验结果对比
3.3 各种算法仿真和分析
针对卫星云图每一像素点与邻域有良好的相似性特点和云团边界像素点方块单元的结构重复概率很大的特征。选用方块编码(BTC)与可逆元胞自动机算法(RCA)结合算法,简洁实用。
本文测试的十余幅云图均为FY2E红外图像,数据格式如前所述。本实验中分别用方块编码(BTC)与多子带可逆元胞自动机算法(RCA)结合的RCA-BTC算法和方块编码与有限加权元胞自动机算法(WFCA)结合的WFCA-BTC算法。分块大小是2×2和4×4。调整方块单元总的灰度差值,用峰值信噪比(PSNR)作为误差阈值与原图进行比较,得出方块单元总的灰度差值为10是最佳值。图6是对结果进行比对。

图6 2017年7月FY2E红外图像实验结果对比(上排为原始图,下排为对应的仿真图)
从表2可见,RCA-BTC算法压缩效果良好,随着分块变大,压缩效果变好,分块为4×4的RCA-BTC压缩率最高。此外,云图的重建质量RCA-BTC(2×2分块)最高,多幅图像的峰值信噪比(PSNR)和均方差(RMS)比较满意。在达到较好图像质量的条件下压缩比最好的是RCA-BTC(4×4分块)。
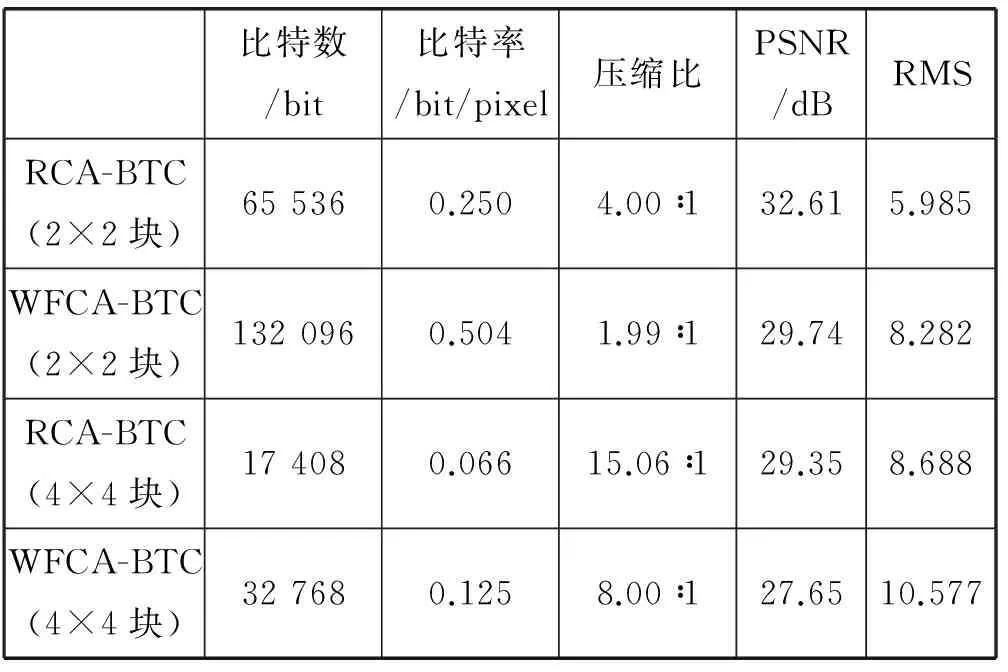
表2 两种编码算法仿真效果比较
这里只对数据格式为二进制的大小为262 144 bit,256级灰度值云图进行实验对比。如果采用同样像素的大小为1 035 264 bit十进制的云图数据文件,那么压缩比可以达到50∶1。
4 结 语
本文采用方块编码与自动机结合的方法进行卫星云图数据的压缩,针对卫星云图的特性,改进算法,使之简洁实用。实验对比表明,在尽可能保留云图质量的前提下,达到了比较满意的信噪比和压缩比。
下一步可以根据卫星云图灰度值分布特征,修正均值编码规则等。例如256级灰度值的150到200级的区间划分得更细一些,使之更适合云系和云团的图像重建。
[1] Kunt M,Johnsen O.Block coding of graphics:A tutorial review[J].Proceedings of the IEEE,1980,68(7):770-786.
[2] 曹青,吴乐南.利用JPEG-LS高效无损压缩气象卫星云图数据[J].应用气象,2002,13(3):380-382.
[3] 叶红,安东升.基于小波变换的卫星云图压缩方法[J].计算机工程与科学,2004,26(10):60-65.
[4] 曾党泉,王员云,赖培辉.基于九宫格的二值图像压缩算法[J].计算机应用与软件,2015,32(7):259-263.
[5] 张方舟,王徐研,郝庆辉.基于遗传分形编码的嵌入式小波图像编码算法[J].计算机技术与发展,2015,25(1):128-132.
[6] 田振川,李冠朋,王蒙蒙,等.基于遗传算法的分形图像压缩技术研究[J].计算机应用与软件,2013,30(4):138-140.
[7] 方翔,王新.小波变换在气象卫星云图压缩中的应用[J].应用气象学报,2010,21(4):423-432.
[8] 张爱华,常康康.结合DCT补偿的分形图像编码[J].计算机技术与发展,2014,24(1):61-64.
[9] 张建伟.气象卫星云图的分形编码研究[J].南京气象学院学报,1998,21(3):328-334.
[10] 黄鹏涛,陈贤富.基于元胞自动机模型的新型二值图像压缩算法[J].计算机系统应用,2010,19(12):75-80.
[11] Kari J.Theory of cellular automata:A survey[J].Theoretical Computer Science,2005,334(1-3):3-33.
[12] Droste M,Kuich W,Vogler H.Handbook weighted automata[M].New York:Springer-Verlag,2009.
[13] Toffoli T,Margolus N.Invertible cellular automata:a review[J].Physica D:Nonlinear Phenomena,1990,45(1-3):229-253.
[14] 吴慧琳,周激流,龚小刚.基于多子带可逆细胞自动机的二值图像压缩算法[J].计算机应用研究,2013,30(5):1547-1550.
[15] 刘跃霞,刘耀军,阎金瑶.数字图像的加权有限自动机表示[J].太原师范学院学报,2010,9(2):52-55.
[16] 陈欢青,马小虎.基于广义有限自动机的图像压缩方法[J].计算机应用与软件,2003,26(3):230-233.
